悬吊多质量摆体系力学机理及减振性能试验研究

孙澔鼎, 何浩祥, 程 扬, 张耀源, 曹 青

(北京工业大学 工程抗震与结构诊治北京市重点实验室,北京 100124)

传统调谐减振控制装置[1-2]包括调谐质量阻尼器(tuned mass damper, TMD)、调谐液体阻尼器(tuned liquid damper, TLD)和悬吊质量摆阻尼器(suspended mass pendulum damper, SMPD)等。TMD由阻尼器、弹簧和质量块构成,通常悬挂或支撑在被控结构上,在其自振频率与结构主频相同的情况下减振效果显著,因而应用广泛[3]。TLD是一种装有液体的调谐装置[4],构造简单、可调性好、成本较低。SMPD是指将质量摆悬吊在主结构上,利用悬吊摆摆动,使其与结构的自振频率接近,实现调谐减振,从而减小结构的动力响应。相对于TMD与TLD,悬吊质量摆具有减振效果明显、构造简单、机理明确及布置便捷等优点,因此具有广阔工程应用前景。

鉴于SMPD的优点以及良好的减振效果,研究人员对SMPD的减振机理进行了较为深入的理论与试验研究。李宏男等[5-6]建立了SMPD在多高层结构中的理论力学模型,研究了悬吊摆的不同悬吊方式、摆与结构质量比μ等各项参数对结构减振控制的影响,结果表明,随着摆与结构质量比μ的增加,其减振效果更好。邓洪洲等[7]针对钢结构电视塔风振控制提出一种多悬吊质量摆设计方法,并对其进行优化设计,结果表明,通过优化设计后的多摆结构减振效果较好。Setareh等[8-9]建立了摆式TMD的等效单自由度模型,并通过理论与试验验证了其调谐减振的可能性,并将半主动磁流变学装置应用于摆式TMD系统中,以控制楼层的过度振动,通过理论与试验证明了该半主动式摆式阻尼器减振效果良好。Roffel等[10-11]通过研究非线性摆式TMD三维运动与柔性多自由度结构耦合的动力响应,提出一种对现有摆式TMD进行状态评估的程序。侯洁等[12-13]针对悬吊摆小摆角线性分析的局促性,提出大摆角非线性计算方法,将质量摆线性刚度修改为非线性,结果表明,在不同场地条件下,均有明显的减振效果。Huang等[14]建立了单自由度结构空间悬挂质量摆模型的耦合动力学方程,对摆的振动特性及性能进行了数值分析,结果表明悬挂质量摆对输电塔的地震响应有明显的削弱作用。霍林生等[15]提出一种被动式自适应悬吊摆,研究了其对单层网壳结构在不同的水平和竖向地震作用下的减振效果,结果表明该自适应悬吊摆大摆角时减振效果明显好于传统悬吊摆。

上述研究均证明了SMPD具有良好的减振效果,并可以通过半主动控制、非线性刚度修改及自适应悬吊等方式进一步加强其减振性能,但SMPD存在调谐频带较窄、长周期结构中调谐摆长过长而短周期结构中摆长过短等状况,如台北101大厦的基频约为0.147 Hz,为达到悬吊摆阻尼器频率与结构基频相同,摆长被设计为11.5 m,实施困难、占地空间大;对于基频为2 Hz的低矮楼层,SMPD的最优摆长为0.062 m,摆长过短,不适用于工程实际。综上,SMPD在工程实际中难以直接应用,因此悬吊质量摆的工程可行性问题亟待解决。

为解决SMPD频带较窄问题,闫维明等[16]通过将多个附加弹簧与质量块相连,实现SMPD对河南艺术中心标志塔多向振动控制,试验结果表明该装置可以明显减小塔的风致响应,同时可以通过调换弹簧刚度与位置方便调整阻尼器的频率,但由于只设置一个质量块,无法对塔实现多阶频率调谐和多振型控制。Gerges等[17]将传统TMD中的弹簧和阻尼部分换成钢索弹簧,形成悬吊式钢索弹簧SMPD,试验研究表明,通过该方法可以很好地改善摆式阻尼器频率较窄的问题。对于工程摆长可行性问题,秦丽等[18]提出一种摩擦式SMPD,通过设置碟形弹簧与摩擦阻尼片,可实现SMPD刚度与摆长调节,并提高质量块在摆动过程中的稳定性,但该种SMPD摆长调节长度范围较窄,不具备灵活性。Kurino等[19]提出一种悬吊摆式TMD,当TMD达到某特定速度时,阻尼器内的液体内特定的压力使部分内置阀门打开或关闭,从而主动控制TMD的摆动幅度,虽然该方法可以调节摆长,从而满足工程可用性,但操作方法较难,不易在工程实际中使用。Huber[20]提出了一种双摆箱型调谐阻尼器,其附加的橡胶阻尼给双摆箱型TMD的活动范围提供了限位,解决了传统悬吊摆安装空间大等问题与双摆摆长问题,并已得到应用。上述两种悬吊摆与TMD相结合的方式可以部分解决摆长问题,但在实际可行性和效果上仍需进一步深入研究。

综上所述,尽管目前在增强悬吊质量摆阻尼器减振控制效果等方面已取得一定的成果,但在改善悬吊质量摆阻尼器多阶调频能力以及摆长问题,现阶段仍处于理论探究阶段,尚没有形成较为成熟的理论依据以及可靠的试验结果来指导工程实际设计与应用悬吊质量摆阻尼器,亟需对其进行机理分析和试验验证。有鉴于此,本文在现有的研究成果之上,提出将串联或并联式悬吊多质量摆通过弹簧与结构墙体连接,实现灵活调整SMPD的刚度,从而达到多阶频率调节以及改善摆长的问题。通过构建各类型悬吊质量摆阻尼器的力学模型,对各种类型悬吊摆的动力性能进行理论分析,并建立各类型悬吊摆结构体系的动力方程,通过对典型结构进行理论分析与振动台试验,对比分析了各类悬吊质量摆的减振性能,阐明了装有弹簧的悬吊多摆阻尼器具有多阶调谐能力以及改善摆长的特点,并对结构减振控制具有明显的优越性。

1 各类悬吊质量摆动力特性分析

结合已有研究,本文列举了不同形式的附加刚度的悬吊质量多摆,如图1所示。质量块通过刚性吊杆及万向铰支座与结构楼板相连接。具有两个质量块串联作用的双摆结构模型见图1(a)及图1(c),质量块通过刚性吊杆、万向铰支座与结构楼板相连接,附加弹簧的双摆称为悬吊弹簧双摆,无附加弹簧的双摆称为悬吊无弹簧双摆,两种摆统称为串联形悬吊双摆,两者的差别为:悬吊弹簧双摆的调谐质量通过弹簧与结构墙体相连接,连接方式为螺栓锚固连接,通过合理设置SMPD质量块的调谐质量大小m、各段刚性吊杆长度l和弹簧刚度k,可以使该SMPD的前两阶自振周期与结构的前两阶周期接近,从而实现对结构多阶频率调谐减振,降低结构动力响应;悬吊无弹簧双摆中调谐质量并没有配置弹簧,因此不具备调整刚度的能力,也就不具备灵活调整前两阶自振周期的能力。具有两个质量块并联作用的双单摆结构模型见图1(b)及图1(d),附加弹簧的双摆称为悬吊弹簧双单摆,无附加弹簧的双摆称为悬吊无弹簧双单摆,两种摆统称为并联型悬吊双单摆,两者的差别与上述两种双摆的差别相同,不再赘述。

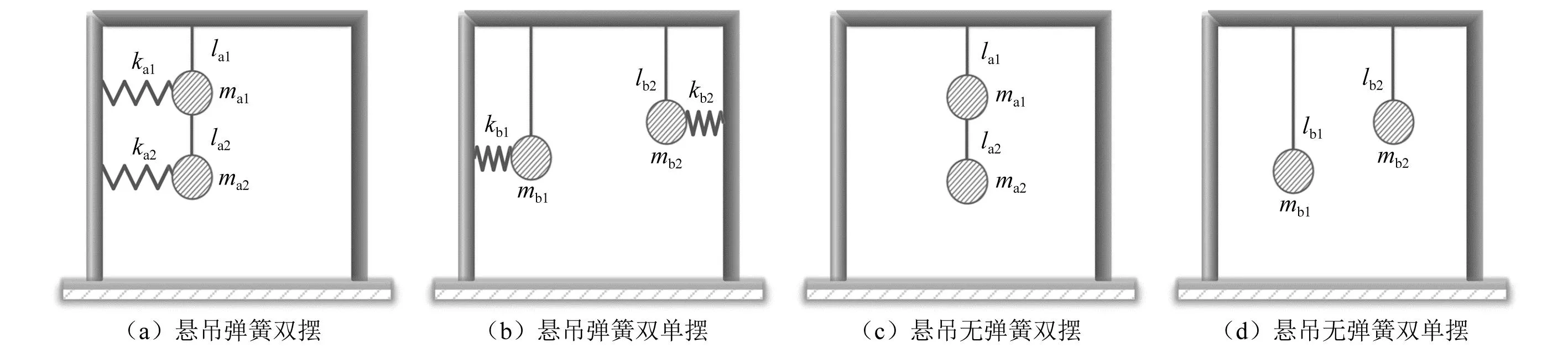
图1 四种悬吊多摆简图Fig.1 Diagram of four suspended multi-pendulums

如图1(a)所示双摆体系的自由动力方程为

(1)

式中:ma1和ma2分别为悬吊弹簧双摆两个质量块的质量;la1和la2为弹簧双摆刚性吊杆长度;ka1和ka2为弹簧双摆中与两个质量块连接的弹簧刚度;xa1和xa2分别为弹簧双摆两个质量块对地面的相对位移。

由式(1)可获得悬吊弹簧双摆的前两阶频率解析表达式为

(2)

当ka1=ka2=0、ma1=ma2=m且la1=la2=l时,即得到悬吊无弹簧双摆(见图1(c))的前两阶频率解析表达式

(3)

式(3)表明:对悬吊弹簧双摆的自振频率影响要素包括附加的弹簧刚度、刚性吊杆长度以及质量块的质量,通过合理调节以上三要素,可以有效的调节悬吊弹簧双摆的多阶频率实现对结构的多阶调谐减振。而影响悬吊无弹簧双摆自振频率的为刚性吊杆长度以及质量块质量,由于缺少弹簧附加刚度的调谐作用,悬吊无弹簧双摆的减振频带范围相较于悬吊弹簧双摆较窄。

针对图1(b)所示模型中的双单摆体系进行动力学建模,相应的体系自由动力方程如下

(4)

式中:mb1和mb2分别为悬吊弹簧双单摆两个质量块的质量;lb1和lb2为弹簧双单摆刚性吊杆长度;kb1和kb2为弹簧双单摆中与两个质量块连接的弹簧刚度;xb1和xb2分别为弹簧双单摆两个质量块对地面的相对位移。

弹簧双单摆的前两阶频率解析表达式为

(5)

当kb1=kb2=0、mb1=mb2=m及lb1=lb2=l时,即得到悬吊无弹簧双单摆(见图1(d))的前两阶频率解析表达式,如下

(6)

式(6)表明:对悬吊弹簧双单摆的自振频率影响要素包括附加的弹簧刚度、刚性吊杆长度以及质量块的质量,通过合理调节以上三要素,可以有效调节悬吊弹簧双摆的多阶频率实现对结构的多阶调谐减振。而无弹簧双单摆频率与单摆相同,由于两个摆同时发生晃动,当限定摆质量的情况下,可以通过调整两个摆的摆长来实现对结构的调谐减振,相较于单摆可以实现多阶频率控制。

综上,两种形式悬吊弹簧多摆的频率与质量块质量、刚性吊杆长度和弹簧刚度均相关。相较于传统悬吊单摆、无弹簧串、并联型悬吊多摆,附加弹簧的串、并联型悬吊多摆可通过优化调节上述三种要素,实现其各阶自振频率与被控结构前几阶自振频率相同或接近,增加其调谐减振的频带范围的同时,又可灵活调整摆长,更适用于工程实际应用。在实际应用下,可根据结构顶层层高首先确定合适的摆长,再通过式(1)和式(4)确定附加弹簧的串、并联型悬吊多摆的附加弹簧刚度,从而确保两种悬吊多摆的频率与结构基频一致。若存在多组摆长和刚度满足频率要求,可任意选择一组即可。

2 具有悬吊多摆的减振结构动力方程

为了更加合理地评价各类悬吊质量摆的减振性能,充分研究其与被控结构共同作用的动力特性和减振机制,本文以顶层分别安装有悬吊弹簧双摆、悬吊弹簧双单摆、悬吊无弹簧双摆、悬吊无弹簧双单摆的框架结构为研究对象,建立结构动力方程。布置四种类型摆的体系整体简化模型如图2所示。图2中:mi和ki分别为结构各层的质量和刚度;kp1和kp2分别为悬吊摆的附加弹簧刚度;mp1和mp2为悬吊摆质量块的质量;l1和l2为摆长。当结构在地震作用下振动时,其楼层顶部装有的各类型悬吊质量摆的质量块会随着结构的振动而发生摆动。

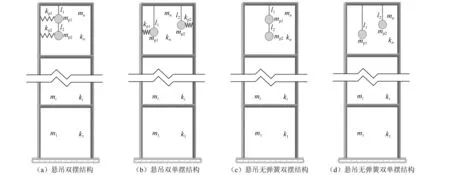
图2 四种带有悬吊双质量摆的结构体系示意图Fig.2 Structure systems coupled with four types of double mass pendulums damper

装有四种类型摆的结构体系在质量块随地震作用下往复摆动的运动方程为

(7)

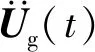
(8)

(9)

(10)

(11)

各质量矩阵均可表示为M=diag[m1,m2, …,mn,mp1,mp2],其中diag为对角阵。被控主体结构阻尼阵Cs可采用Rayleigh阻尼矩阵表示,各类悬吊摆的阻尼cpi=2mpiωpiζpi,mpi为各类悬吊摆中各质量块的质量,ωpi为各悬吊摆的圆频率,其中阻尼比ζpi可根据Den[21]提出的最优阻尼比ζpo求得,即

(12)

式中,μ为各悬吊摆与被控结构的质量比。总阻尼矩阵可表示为

(13)

(14)

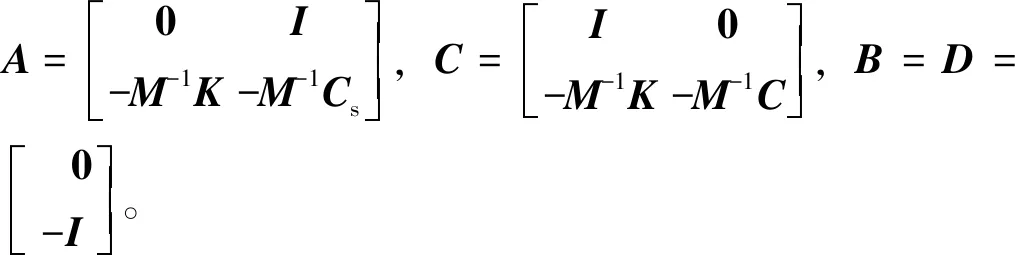
3 算例分析及性能验证

为了对比分析各类悬吊多摆-多层结构系统在地震动作用下的减振效果以及多阶调谐减振的能力,本文选取各层质量和刚度均相同的钢筋混凝土10层框架结构为被控结构,分别采用悬吊单摆、悬吊弹簧双摆、悬吊弹簧双单摆、悬吊无弹簧双摆、悬吊无弹簧双单摆五种类型摆对其进行减振,通过数值模拟,来验证装有弹簧的悬吊多摆具有多阶调谐减振的能力。

被控结构为10层框架结构,各层层高4 m,平面尺寸为30 m×30 m,各层的质量为4×105kg,各层刚度为5.5×105kN/m。将各类悬吊摆阻尼器安装于结构顶层,五种类型摆总质量均取结构总质量的2%,其中各类双摆的两个摆球的质量均相同,即为结构总质量的1%,如图3所示。结构的前两阶周期分别为1.134 s和0.357 s,主控振型为第一阶振型,通过调节刚性吊杆长度,将悬吊单摆的自振周期调整为1.134 s附近,将悬吊无弹簧双摆、悬吊无弹簧双单摆前两阶周期调整为1.134 s和0.357 s;通过调节摆长长度以及弹簧刚度,将悬吊弹簧双摆、悬吊弹簧双单摆的前两阶周期调整为1.134 s和0.357 s。为满足工程实际的需求,经过计算,各种类型摆摆长以及弹簧刚度取值如表1所示。

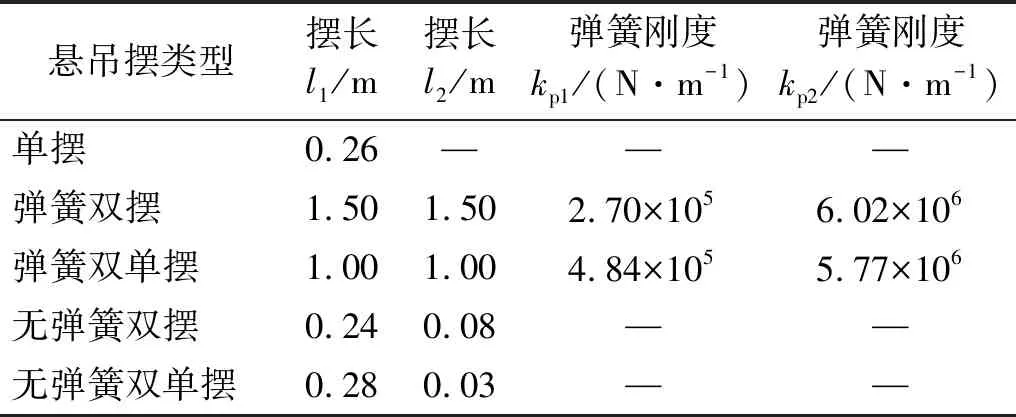
表1 五类悬吊摆参数信息Tab.1 5 category suspension pendulum parameter

对在Cale与El-Centro地震波作用下的结构进行动力时程分析,按照抗震设计要求将两地震波的峰值加速度值调整为0.4g。被控结构在上述两地震波下的结构顶层位移时程和加速度时程对比图,如图4和图5所示。由图4和图5可知,五种类型悬吊摆均可以有效的起到对被控结构调谐减振的作用,其中,悬吊弹簧双摆的减振效果明显更优,其次是悬吊无弹簧双摆,悬吊弹簧双单摆的减振优势并未体现出来,与其余三种传统悬吊质量摆减振效果接近,但其表现出来的可灵活调节摆长长度的能力是其余三种类型摆所不具有的。

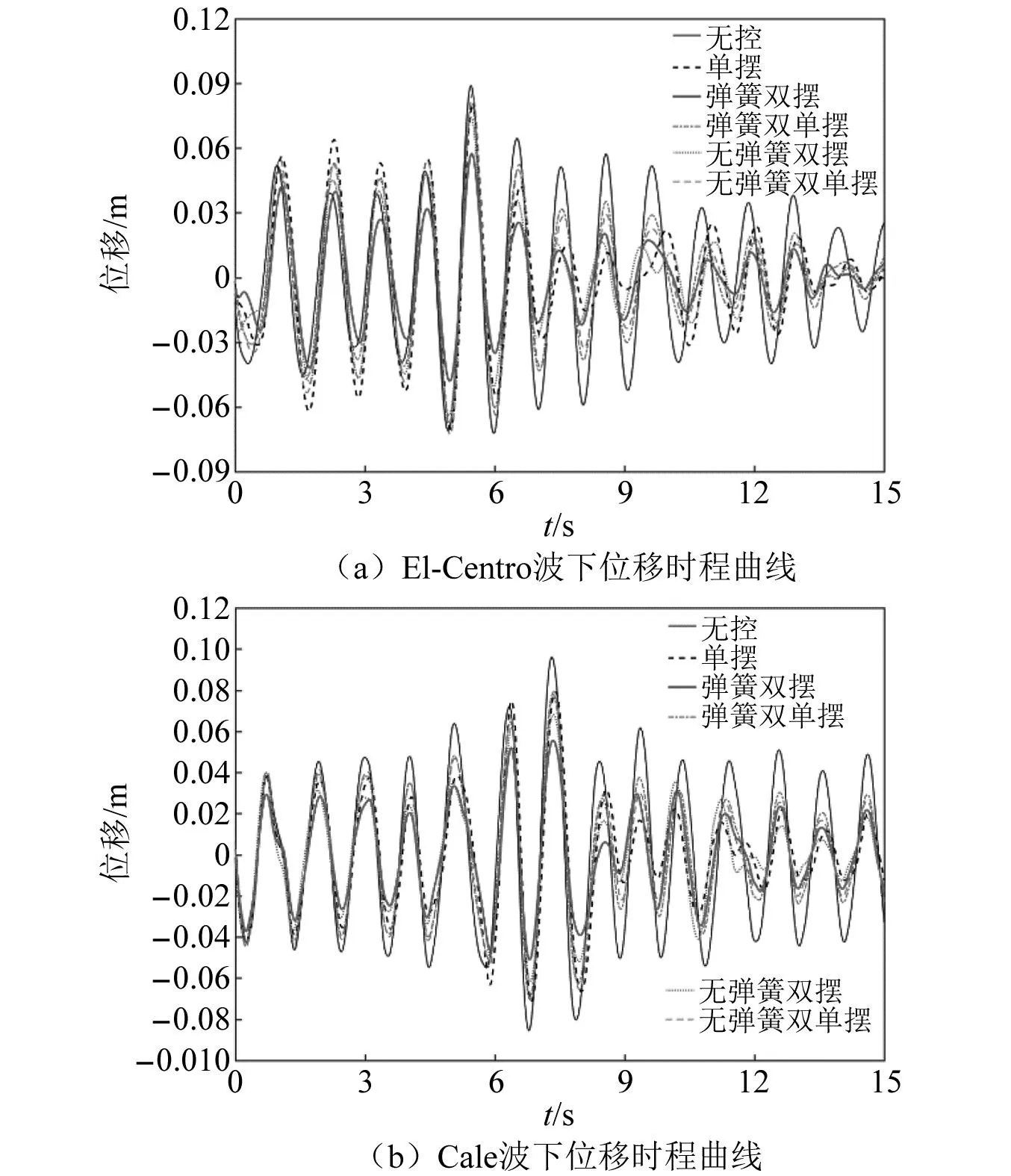
图4 均匀结构顶层位移时程曲线Fig.4 Top displacement history of homogeneous structure

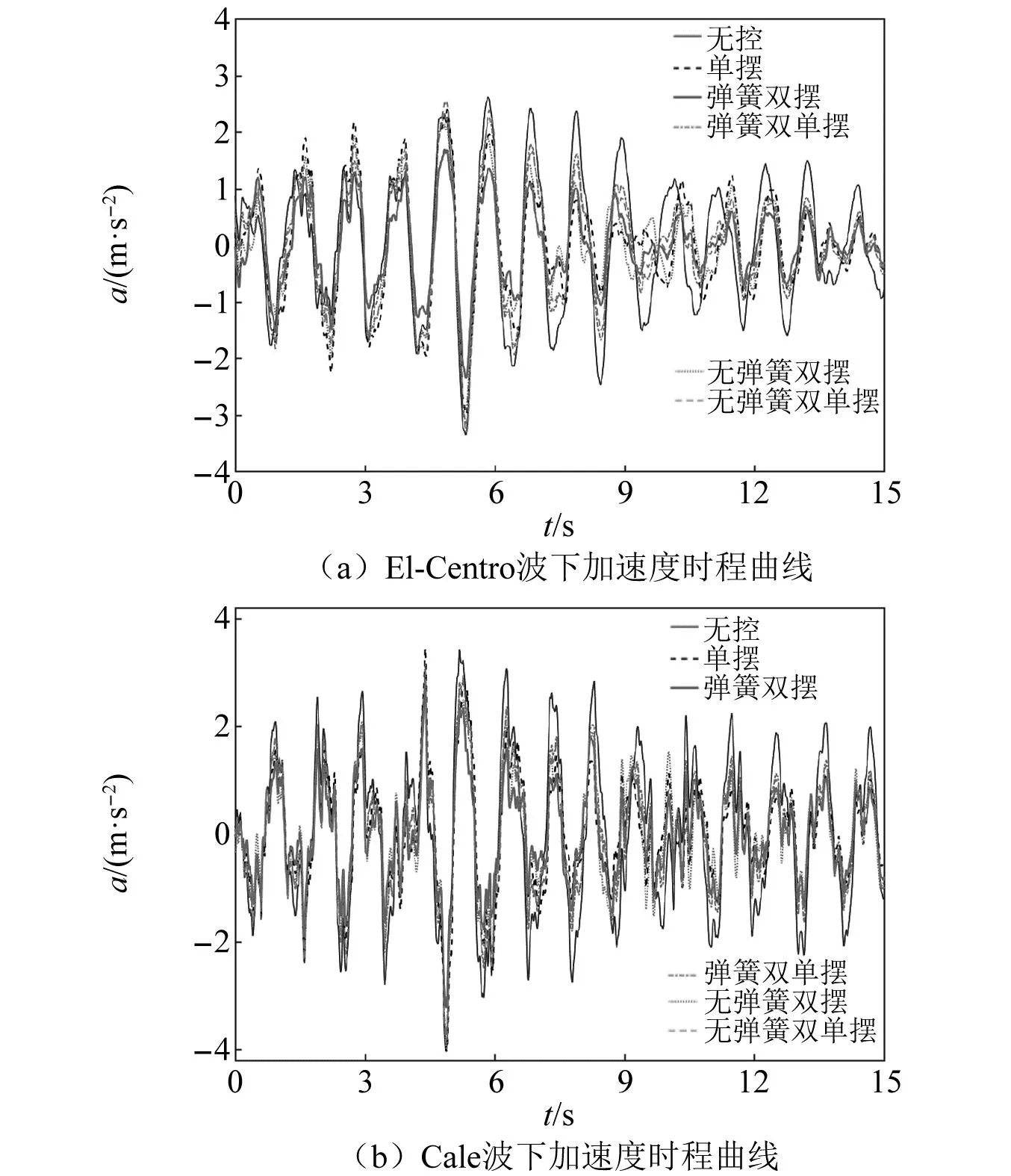
图5 均匀结构顶层加速度时程曲线Fig.5 Top acceleration history of homogeneous structure

附加弹簧双摆与弹簧双单摆的被控结构在El-Centro地震波下的摆角时程曲线,如图6所示。由图6可知:悬吊弹簧双摆上摆的摆角主要在-5°～5°浮动,最大值为12.12°,平均值为2.85°,悬吊弹簧双摆下摆的摆角在全时程下均小于5°,平均值为0.5°,即悬吊弹簧双摆上摆的摆角幅值明显大于下摆,但是下摆的振动频率高于上摆,两个摆共同起到了多阶调谐减振作用;悬吊弹簧双单摆的左摆摆角主要在-5°～5°浮动,最大值为17.57°,平均值为4.57°,悬吊弹簧双单摆的右摆摆角主要在-5°～5°浮动,最大值为5.31°,平均值为0.96°,即悬吊弹簧双单摆左摆的摆角幅值明显大于右摆,但是右摆的振动频率高于左摆,两个摆也共同起到了多阶调谐减振作用。结合被控结构位移时程、加速度时程与摆角时程可得出结论:悬吊弹簧双摆与悬吊弹簧双单摆均基本符合小摆角近似条件(摆角小于等于5°),且摆角高于5°时并未对两类悬吊摆的减振性能产生明显影响,两类悬吊摆均具有较好的多阶调谐减振能力。

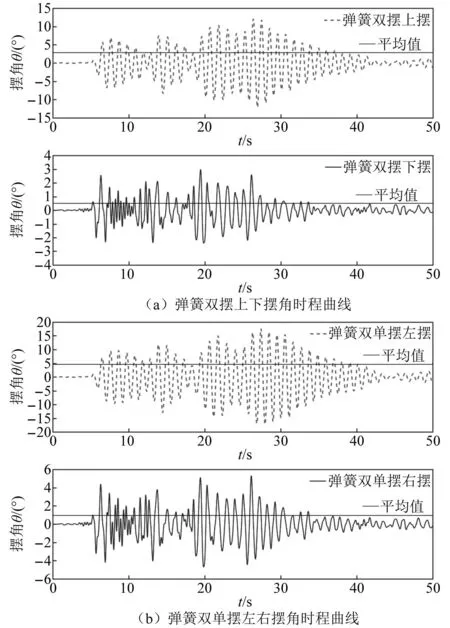
图6 两类弹簧双摆的摆角时程曲线Fig.6 Pendulum angle time curves for two suspended multi-pendulums

被控结构在各类悬吊质量摆控制时的层间位移峰值和层间能量位移(各时间点位移绝对值之和)对比,如图7所示。结果进一步表明:悬吊弹簧双摆的减振效果最佳,悬吊无弹簧双摆虽不具有灵活调节悬吊摆摆长的能力,但其减振效果仅次于悬吊弹簧双摆,可以得到初步结论,即两质量块串联作用的串联形悬吊双摆,减振效果相较于两质量块并联作用的并联形悬吊双单摆以及悬吊单摆更优,且附加弹簧后,其减振效果会得到进一步提升。不过悬吊弹簧双单摆的减振优势虽未体现出来,但其表现出来的可灵活调节摆长长度的能力是其余未加弹簧的悬吊质量摆所不具有的,因此更适用于工程实际应用。

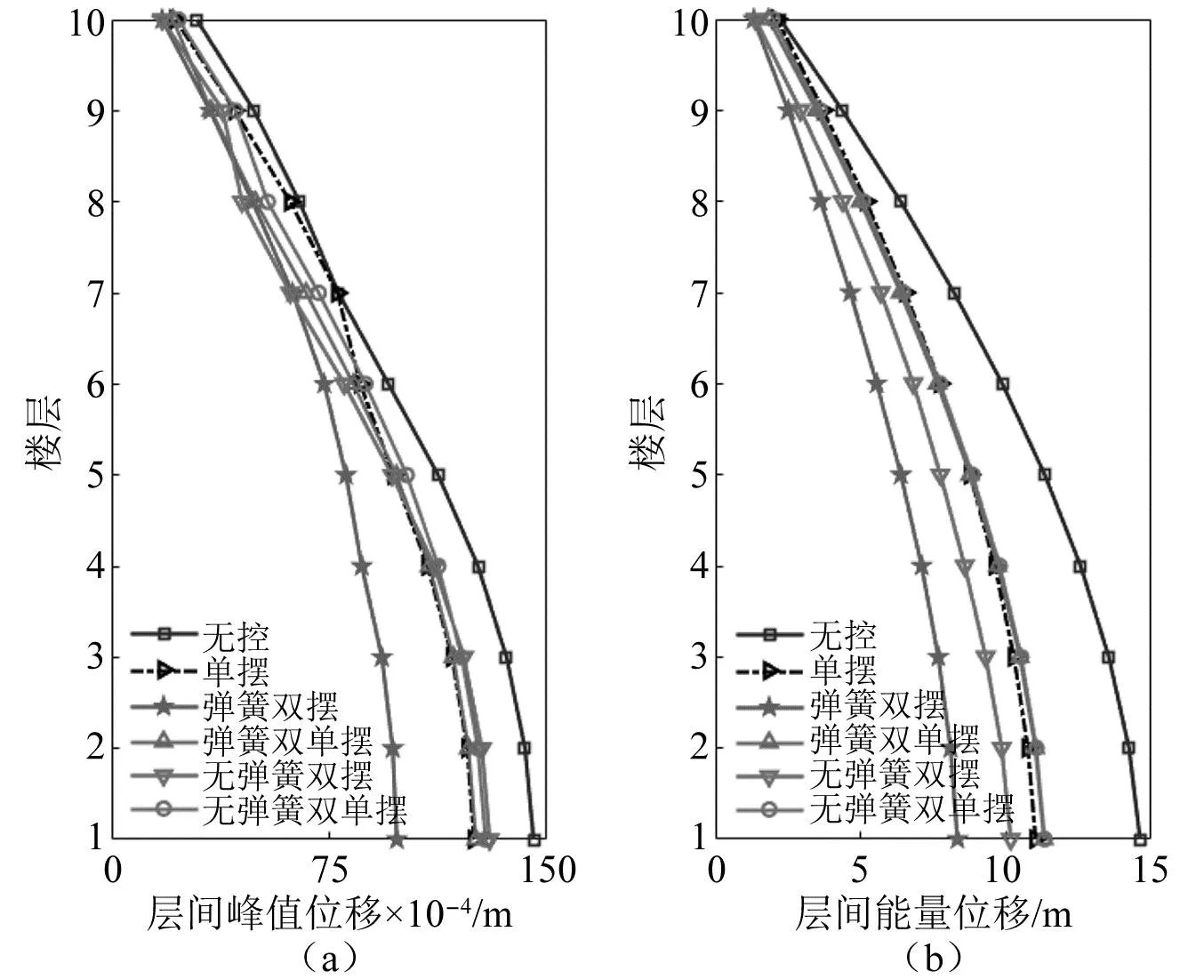
图7 结构层间位移减振效果对比Fig.7 Story drift comparison of structure

为验证各悬吊质量摆多阶调谐减振的能力,选取El-Centro与Cale地震波作用下结构顶层加速度响应的功率谱密度曲线进行比较,如图8所示。无控结构的功率谱曲线峰值和包络面积要远大于各类悬吊摆结构,悬吊单摆与悬吊双单摆、悬吊弹簧双单摆的功率谱曲线峰值和包络面积较为接近,而悬吊弹簧双摆与悬吊无弹簧双摆结构相对较小,从能量角度证明串联形悬吊双摆结构具备更为优越的减振性能。相较于无附加弹簧摆,附加弹簧的串、并联形双摆的结构功率谱曲线峰值和包络面积更小,且对于第二阶频率下的功率谱曲线峰值和包络面积进行对比,附加弹簧的串、并联形双摆明显更小,充分说明悬吊质量摆附加弹簧后可更为有效地提高结构的减振能力并起到了多阶调谐减振作用。

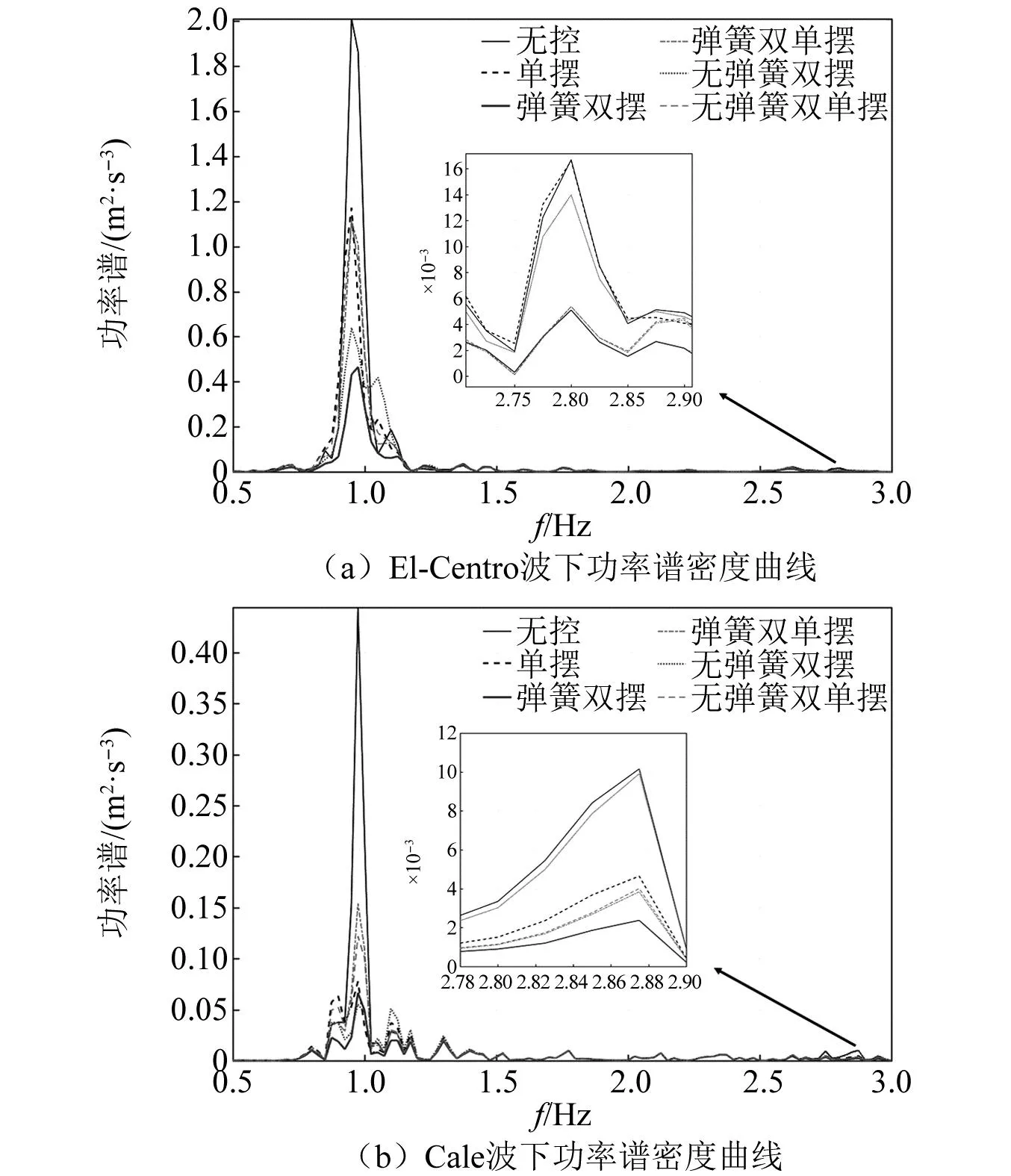
图8 结构顶层加速度响应功率谱密度曲线Fig.8 Power spectral density curve of the acceleration response at the top of the structure

为了更全面地验证各类悬吊摆的减振性能,本文选用4类场地地震波对结构进行动力时程分析,地震波具体信息如表2所示,每类场地选取5条地震波,各地震波地面峰值加速度均调为0.4g。本文定义峰值减震率为无控和有控结构响应最大值之差与无控结构响应最大值的比值;能量减震率定义为无控和有控结构响应包络面积差与无控结构响应包络面积的比值。不同形式悬吊摆在各类场地地震动下平均减震率ζd对比结果如图9所示。

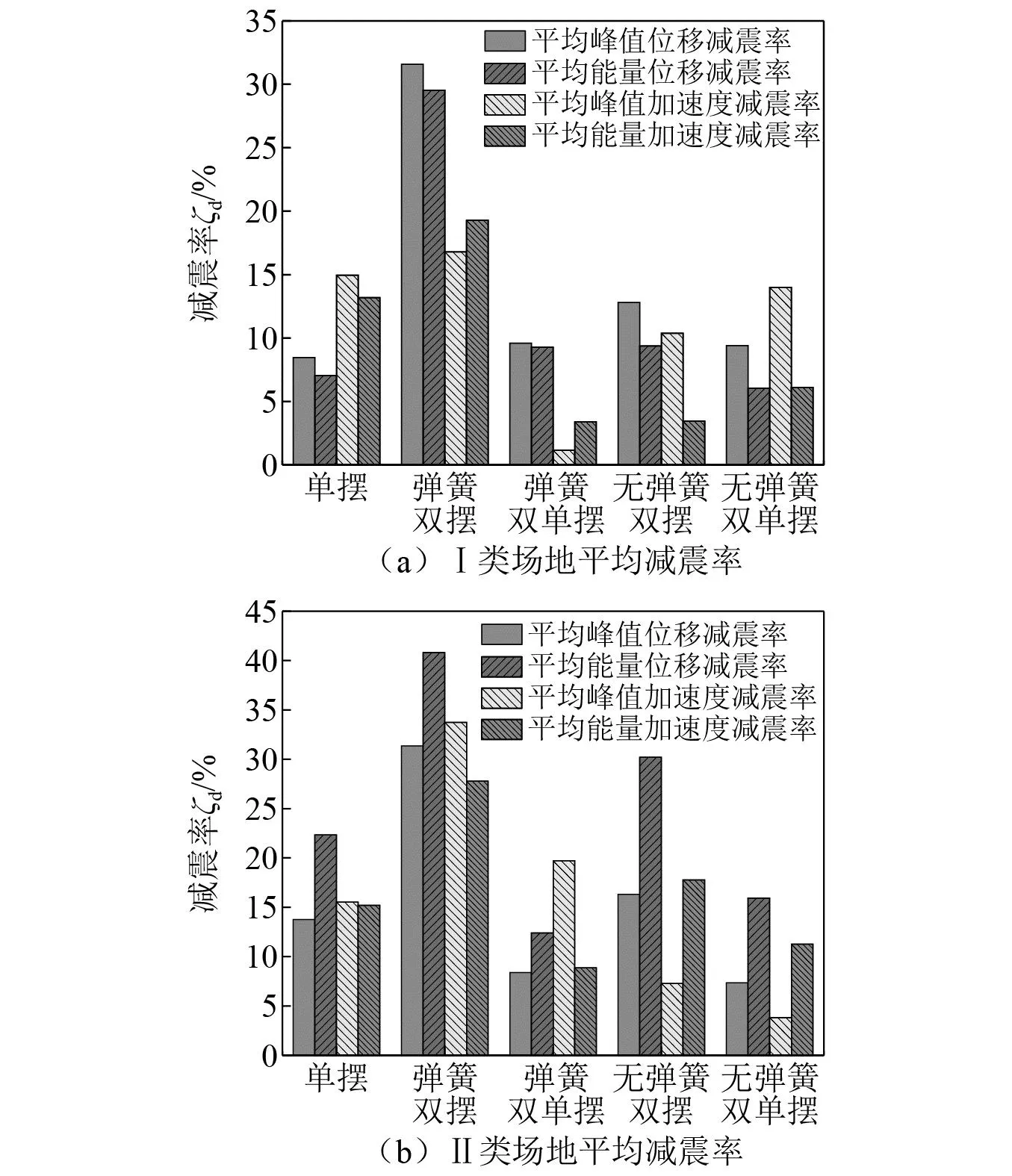
图9 四类场地平均减震率Fig.9 Average damping rate for class four sites

由图9可知,在各类场地地震波作用下,悬吊弹簧双摆的平均减震率最高,悬吊无弹簧双摆其次,并联形悬吊双单摆的减振效果与其相比较差,略等于悬吊单摆的减振效果,但五种类型摆均可以对被控结构实现减振效果。由以上结论可得,串联形悬吊质量摆的减振效果更优,但综合考虑到实际工程中的应用,由于悬吊无弹簧质量摆受限于楼层高度,无法灵活调节其摆长以达到最优的减振效果,因此附加弹簧的悬吊质量摆更具有工程应用价值。经综合对比,串联形悬吊双摆在四类场地地震波下的减振效果最好,而悬吊弹簧双摆因其具备灵活调节摆长的能力,具有更好的工程应用价值。

4 振动台试验分析及性能验证

为进一步验证各类悬吊摆对多层结构的减振性能,本文设计了装有悬吊单摆、悬吊弹簧双摆、悬吊弹簧双单摆、悬吊无弹簧双摆、悬吊无弹簧双单摆的三层钢框架试验模型并进行振动台试验,对比分析装有各类悬吊摆结构在地震作用下的动力响应状况。

4.1 计算模型与参数

试验框架为三层钢结构模型,装有各悬吊摆的结构模型主体框架尺寸相同,楼板采用Q345钢板,尺寸为500 mm×500 mm×6 mm(长×宽×高);柱也采用Q345钢板,横截面尺寸为50 mm×5 mm(长×宽),各柱子间距为390 mm。三层框架模型的首层层高为500 mm,其余层的层高为400 mm,框架柱和楼板通过L型角钢和M6螺栓连接;框架第二层与第三层间加装墙体以满足悬吊弹簧摆中的弹簧与墙体的连接需求,墙体采用亚克力板,尺寸为550 mm×550 mm×10 mm(长×宽×高)。为达到理想的减振效果,确保各悬吊摆力学模型不发生改变,试验中悬吊摆中的附加弹簧已预留出足够的压缩长度,在平衡位置下可达到同时压缩和伸缩,且受压时摆的变形不受限制。试验框架详图如图10所示。

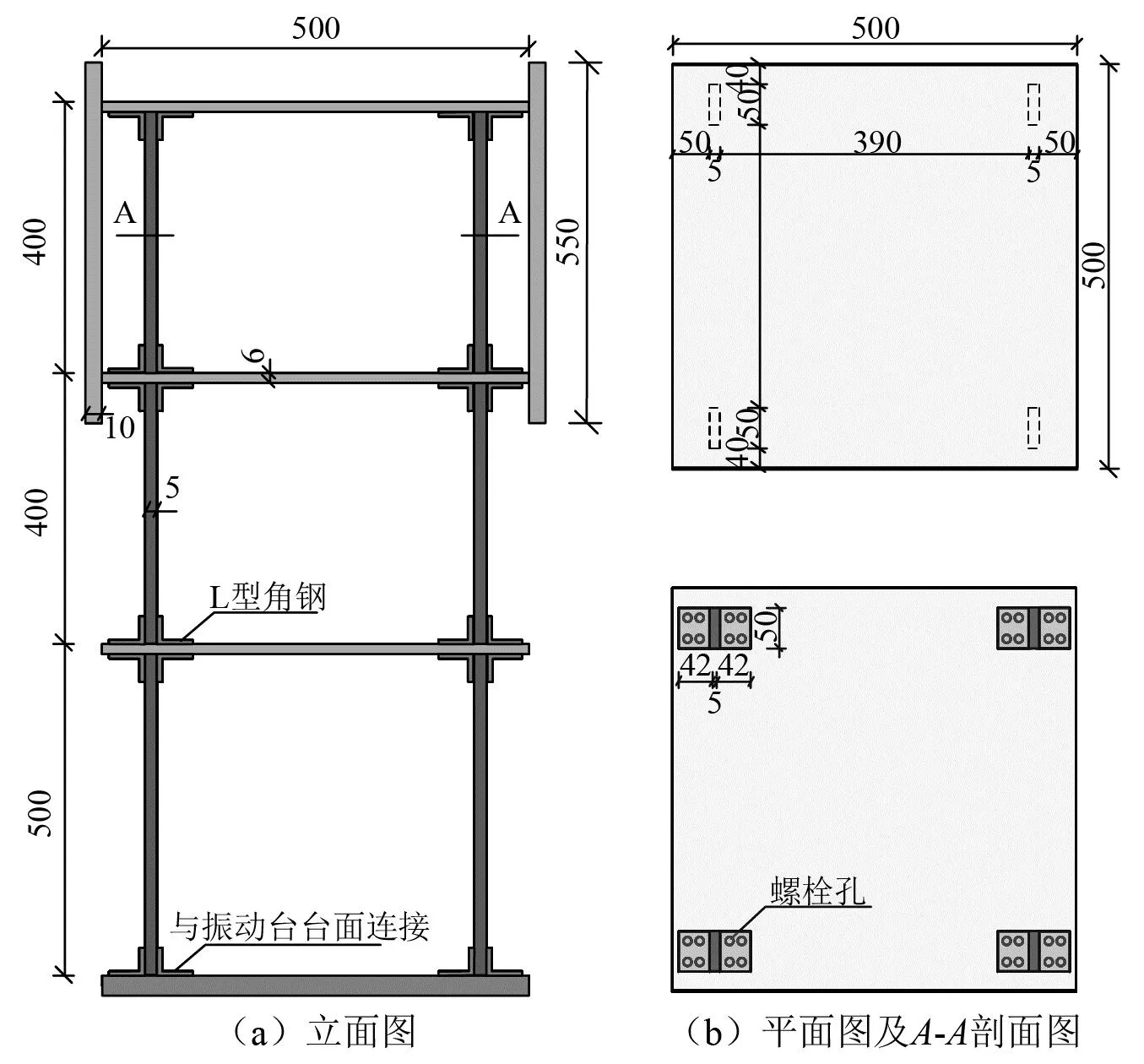
图10 试验框架详图(mm)Fig.10 Test frame details (mm)

质量块与框架顶层楼板采用带孔活结螺杆与M6螺栓闭口螺丝钩连接,连接处可180°旋转,当结构发生振动时,质量块可随着带孔活结螺杆前后摆动,弹簧一端与质量块固接,另一端与墙体通过开口螺丝钩进行连接。悬吊摆与框架连接设计详图,如图11所示。悬吊摆布置在楼板中间位置,以防止受控结构在振动过程中产生扭转。

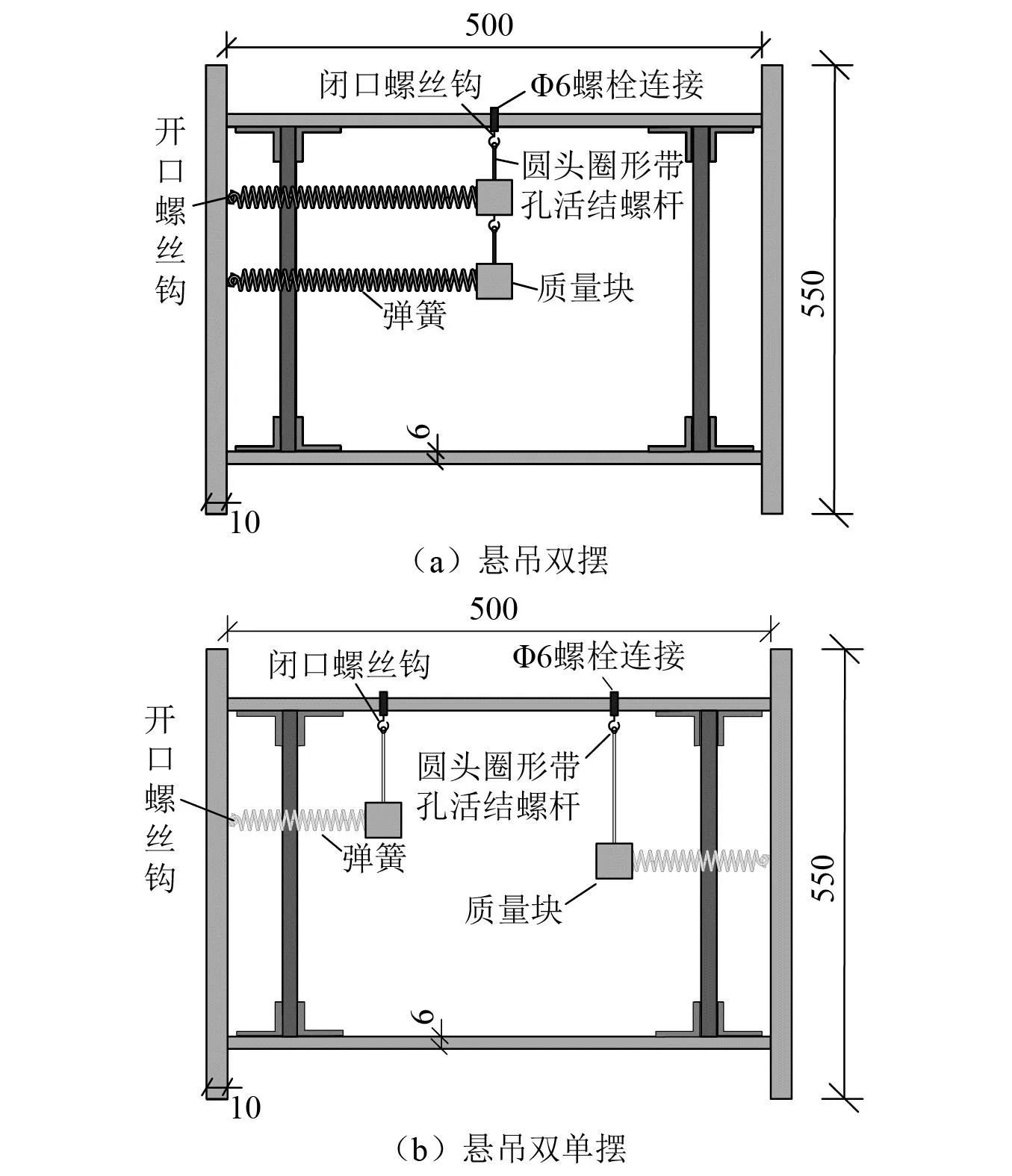
图11 悬吊摆与框架连接设计详图(mm)Fig.11 Details of the design of SMPD connected to the frame (mm)

在顶层楼板分别安装五种类型悬吊质量摆的三层钢框架整体试验模型如图12所示。图中试验设备为单向地震模拟振动台,分别在台面和各楼层沿振动方向均匀布置两个加速度传感器和一个激光位移计测量台面和结构的位移和加速度。钢框架1～3层的质量分别为24.47 kg、23.78 kg和23.78 kg。三层钢框架在白噪声激励下的频率响应曲线,如图13所示,前三阶频率依次为3.97 Hz、14.01 Hz和23.20 Hz。使用自由振动衰减法获得的结构阻尼比为0.38%。完成所有测试后,将白噪声激励重新施加到三层钢框架上。结果表明,结构的频率和阻尼基本不变,表明框架结构在试验过程中没有弹塑性变形。钢框架模型具体信息如表3所示,各悬吊摆摆长以及弹簧刚度取值如表4所示。

表3 钢框架模型信息表Tab.3 Steel frame model information sheet

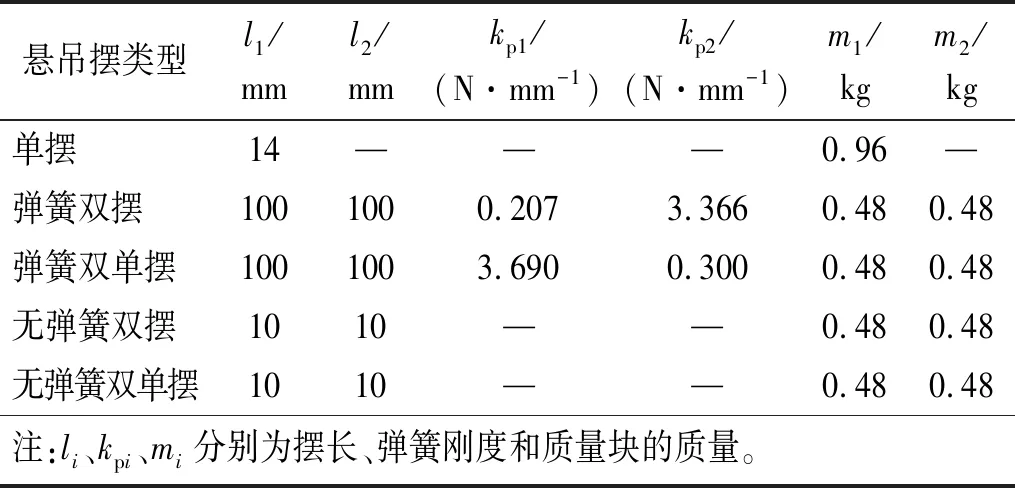
表4 五类悬吊摆参数信息

图12 振动台试验模型图Fig.12 Shaking table test model diagram

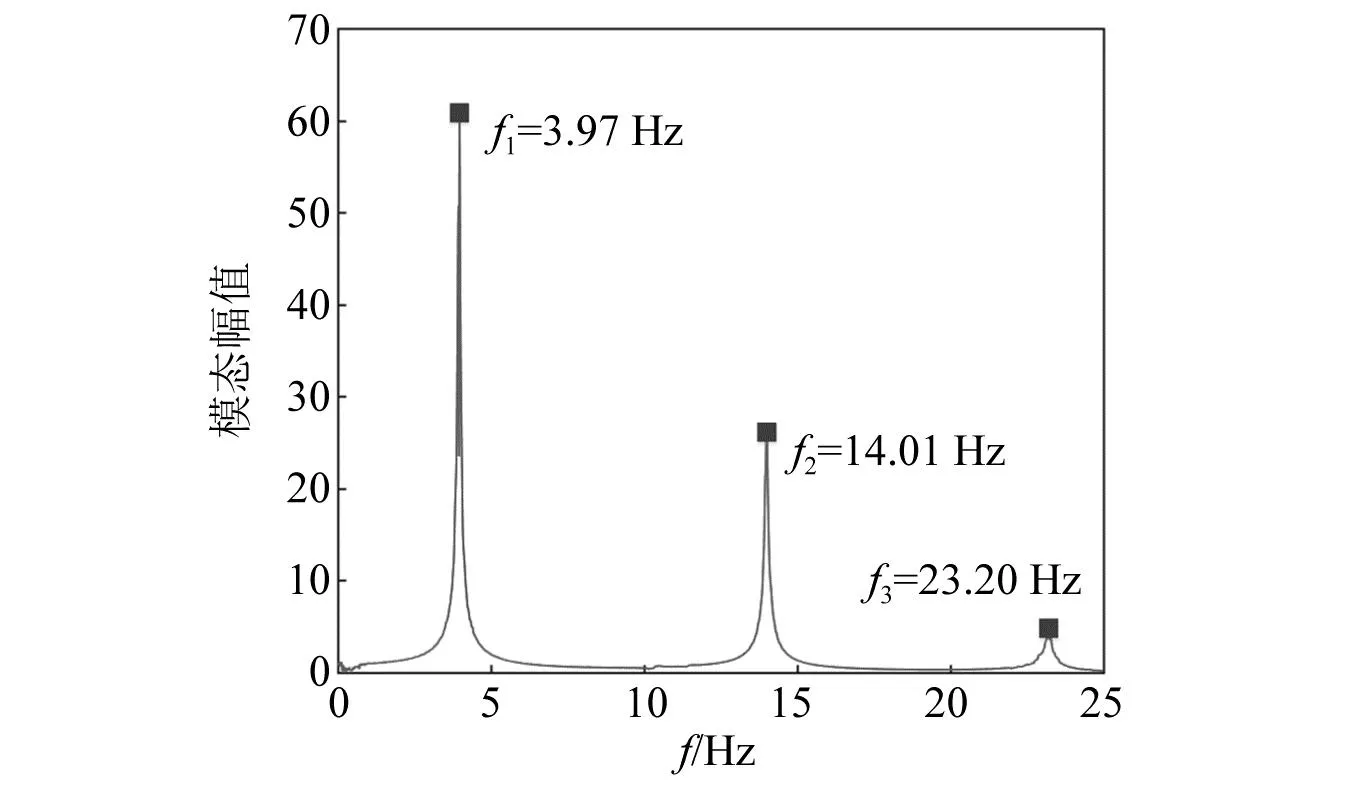
图13 非控结构频率响应曲线Fig.13 Frequency response curve of uncontrolled structure

4.2 试验结果及分析

为验证理论方法的准确性,对简谐激励及El-Centro地震波下无控结构与附加悬吊弹簧双摆与悬吊弹簧双单摆结构的顶层动力响应时程结果进行分析,理论计算结构阻尼比设定与试验测得的结构阻尼比相同,取0.38%,双摆阻尼比根据式(12)求得,ζp1=ζp2=0.36%,结果如图14和图15所示。可发现理论值与振动台试验值高度吻合,理论分析具有良好的精准性。

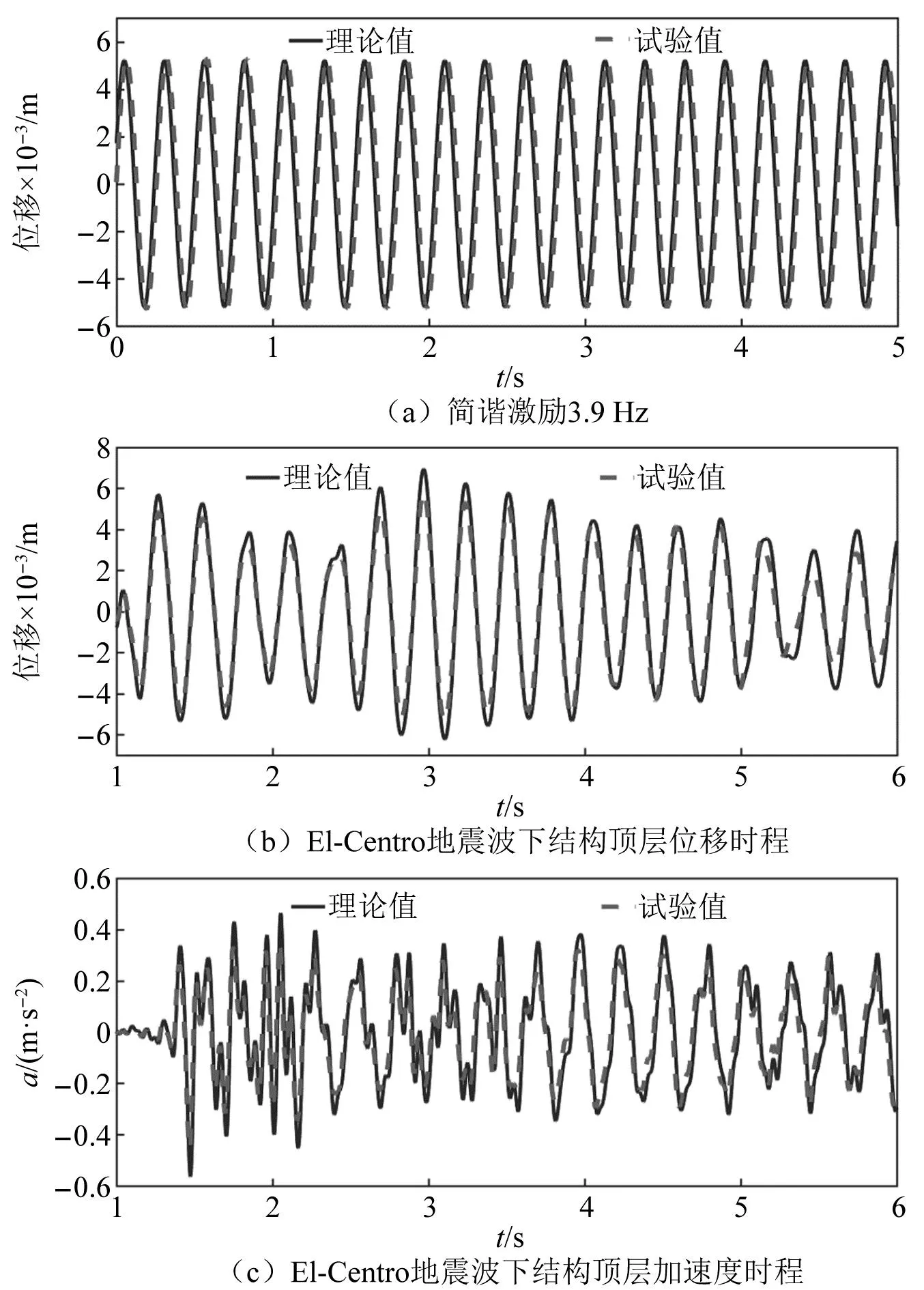
图14 无控结构理论值与试验值对比图Fig.14 Comparison of theoretical and test values for uncontrolled structure

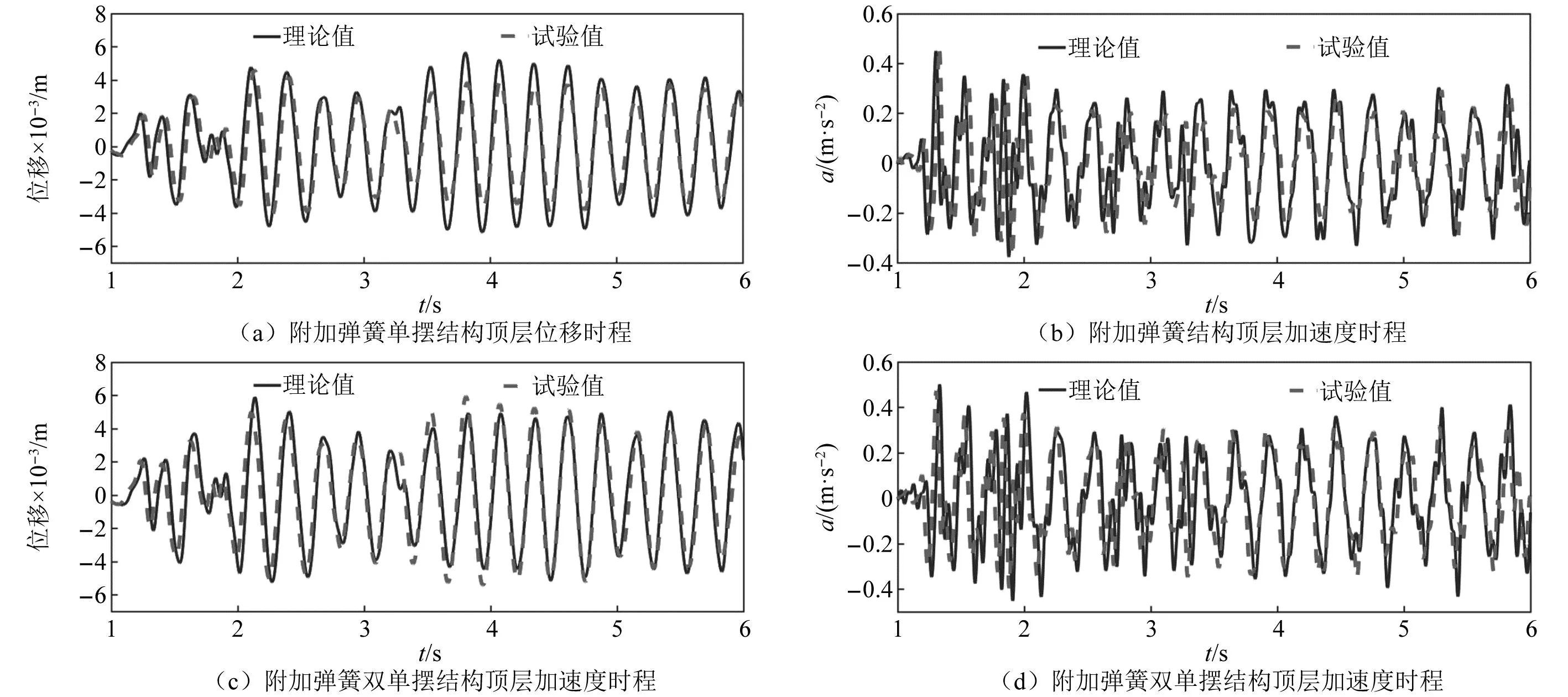
图15 El-Centro波下被控结构理论值与试验值对比图Fig.15 Comparison of theoretical and test values of the controlled structure under El-Centro wave

为了量化理论计算与振动台试验的偏差,采用传统无量纲指标均方根误差(root mean squared error,RMSE)、平均绝对百分比误差(mean absolute percentage error,MAPE)对无控结构理论值与试验值动力分析数据进行误差评估,相关计算式分别见式(15)和式(16)。RMSE表征的含义是测量值与真值曲线的拟合程度,用来衡量测量的准确程度,MAPE越小,测量精度越高。MAPE是衡量模型准确性的统计指标,其值越小表明理论结果越精确。无控结构与被控结构在各激励下动力分析数据误差对比结果,如表5所示。结果表明,理论计算结果与振动台试验结果吻合度高。

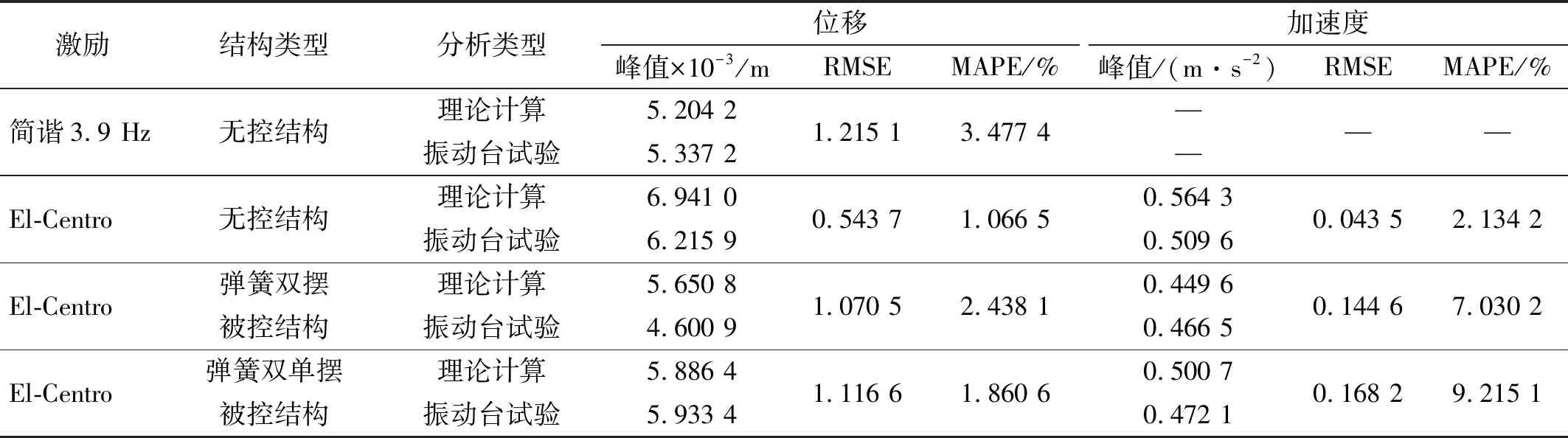
表5 理论计算与振动台试验结果误差对比Tab.5 Comparison of errors in theoretical calculations and shaker test results

(15)

(16)

装有各类悬吊摆试验结构在El-Centro与Clae地震波下的顶层动力时程对比图如图16、图17所示,结果表明,装有各类悬吊摆结构在地震波作用下均有较好的减振效果,其中悬吊弹簧双摆的减振效果最佳,无弹簧双摆的减振效果其次,这充分证明了理论分析所得到的结论:串联形悬吊双摆具有更为优越的减振性能以及弹簧调谐刚度的有效性。

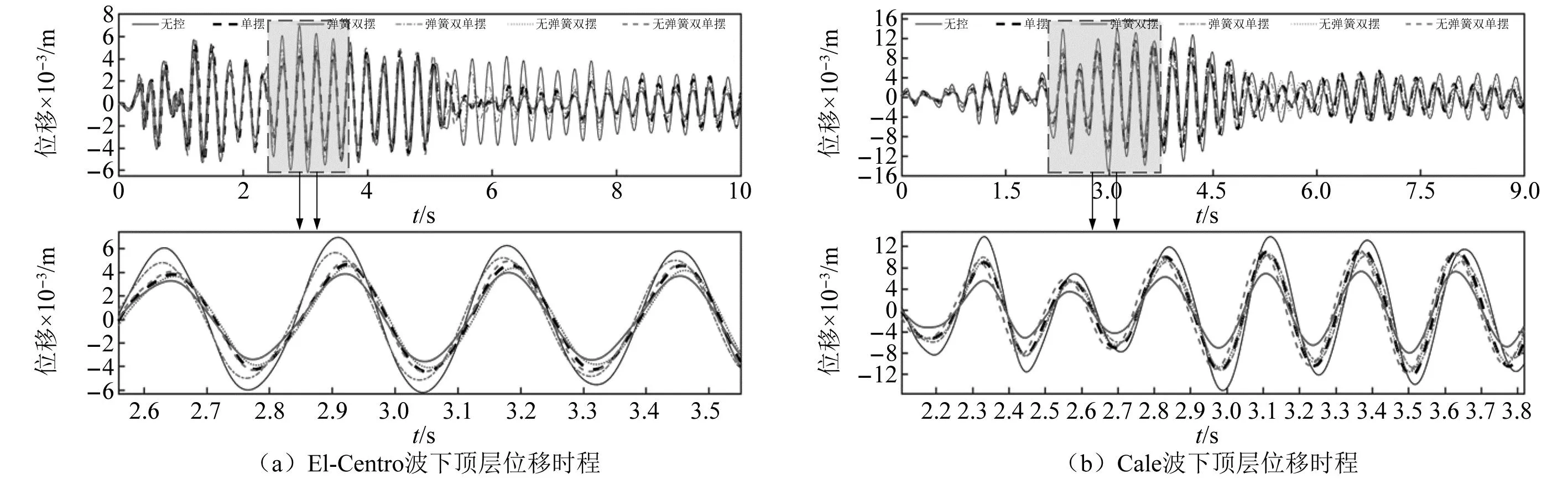
图16 各模型顶层位移时程对比图Fig.16 Comparison of the top layer displacement timescales for each model

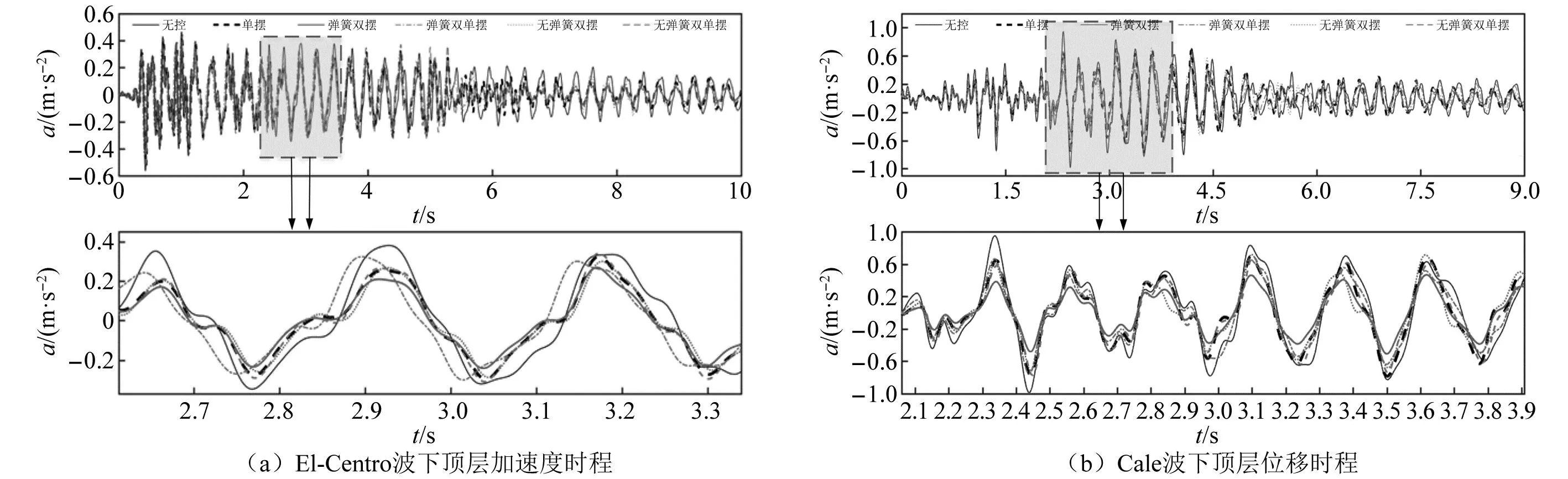
图17 各模型顶层加速度时程对比图Fig.17 Comparison of the top layer acceleration timescales for each model

对装有各类悬吊摆试验结构在El-Centro与Cale地震波作用下结构顶层加速度响应的功率谱曲线进行比较,如图18所示。结果表明:各类悬吊摆均对被控结构一阶振型响应的控制较好,且悬吊弹簧双摆控制体系的前两阶频率下加速度功率衰减最为明显,即悬吊弹簧双摆对结构前两阶频率的控制最为有效,达到了双阶调谐减振;悬吊弹簧双单摆控制体系的前两阶频率下加速度功率衰减也较为明显,但其减振效果并不如意,可证明,悬吊摆附加弹簧后可以更有效的达到多阶调谐减振,但并联形悬吊摆的调谐减振效果不如串联形悬吊摆的形式。其余几个悬吊摆结构相对于无控结构,在前两阶振型下的频域能量也有所衰减,但不如悬吊弹簧双摆,这与理论分析所得到的结果相一致,进一步证明了该力学机理的准确性。

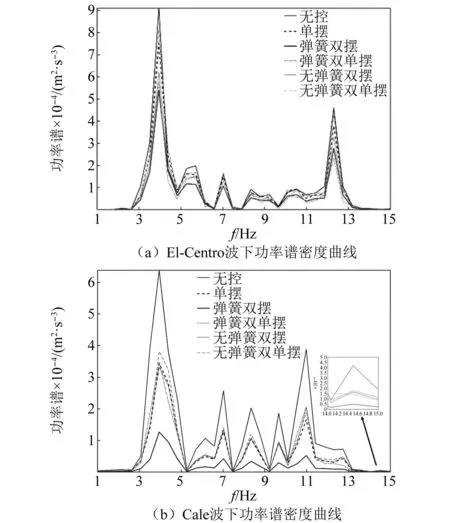
图18 结构顶层加速度响应功率谱密度曲线Fig.18 Power spectral density curve of the acceleration response at the top of the structure

为进一步验证各类悬吊摆对结构具有良好的减振效果和鲁棒性,采用4.1节所选的各类场地地震波作为振动台激励,最终得到不同形式悬吊摆在各类场地地震动下的平均峰值减震率和平均能量减震率,对比结果如图19所示。由图19可知,在各类场地地震波下,悬吊弹簧双摆的减震率最高,其次是悬吊无弹簧双摆,悬吊单摆的减震率与悬吊弹簧双单摆与悬吊无弹簧双单摆基本持平,该结果与上节理论值基本一致,即悬吊弹簧双摆的减振性能最好,其次是悬吊无弹簧双摆,其余三种类型摆减振性能相差不大。

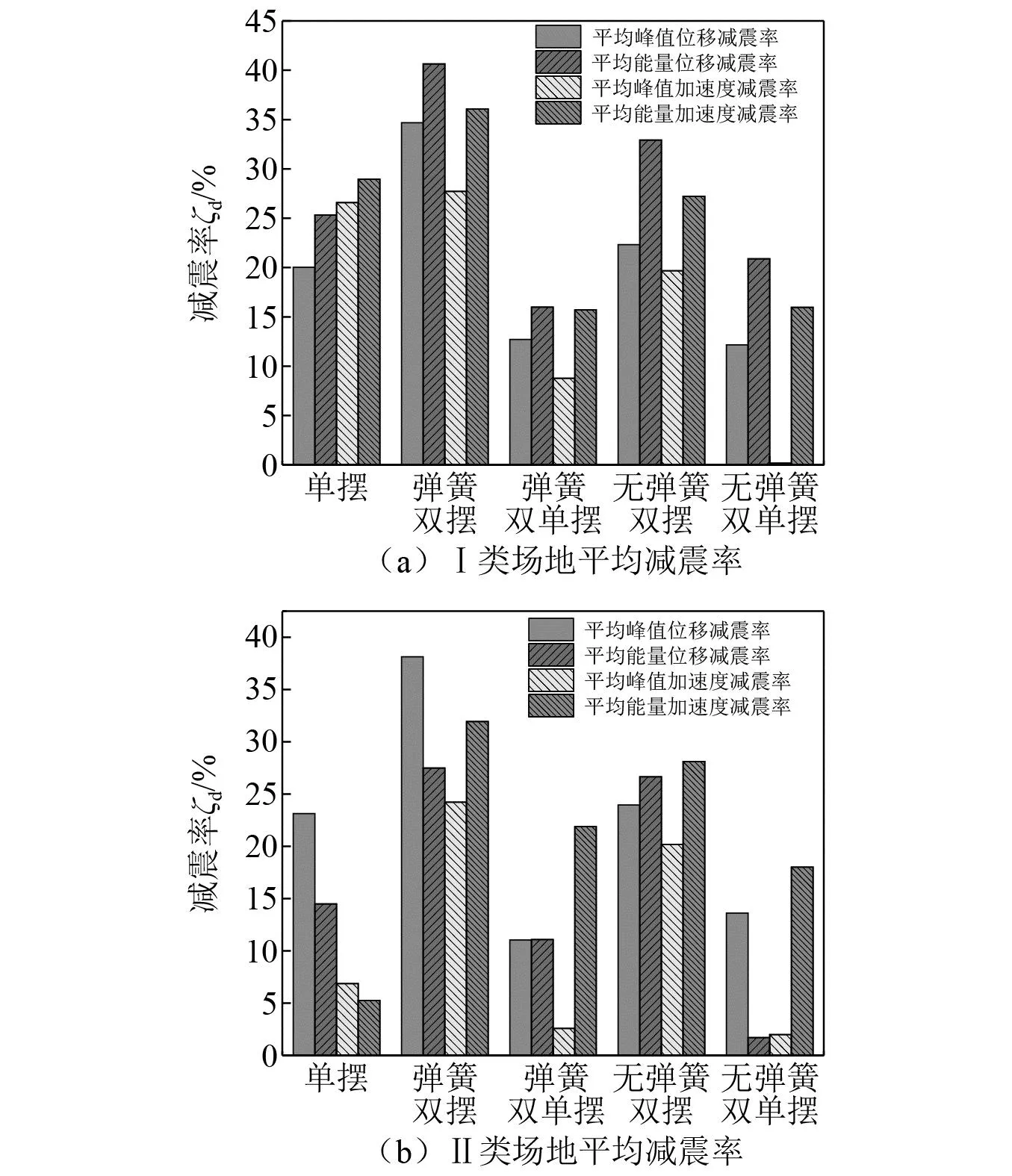
图19 试验四类场地平均减震率Fig.19 Average damping rate for 4 sites

上述试验结果进一步验证了各类悬吊摆对多层结构减振的有效性,也验证了附加弹簧摆对结构多阶调谐控制的可行性,这与前文理论推导一致。由于受到摆长的限制,有弹簧的悬吊摆更适用于工程实际应用,而无弹簧悬吊摆摆长过短,尽管也有一定的减振效果,但实用性差。

5 结 论

传统类型悬吊质量摆阻尼器具有良好的减振性能,但同时拥有摆长无法灵活调节、减振频带较窄等问题,因此在工程实际应用中受到很大的制约。本文提出附加弹簧的串、并联悬吊质量摆,可通过调节弹簧的刚度、质量块的质量和刚性吊杆的长度来实现其最优减振效果,并实现多阶振型的调谐减振控制,由于可以灵活的调整摆长,因此更适用于工程实际。本文选择五种不同类型悬吊摆进行理论与试验研究,建立了各类悬吊双摆的动力方程并进行了动力特性分析,获得了其频率解析解,阐释了其减振机制。在此基础上建立了具有各类型悬吊双摆的结构整体动力学方程。为了验证附加弹簧后串、并联悬吊摆的减振性能与其多阶振型调谐减振的能力,本文建立十层框架模型进行了动力时程理论分析,并构造三层钢框架结构进行振动台模型试验,通过对不同地震波作用下的动力时程响应与功率谱密度分析,经过综合对比得到以下结论:

(1) 附加弹簧的串、并联悬吊多摆可以通过调节弹簧刚度、质量块质量和摆长等多参数实现对被控结构的调谐减振,既能灵活调节其摆长长度也能实现对结构的多阶振型调谐控制。理论分析表明:五类悬吊质量摆中,两种串联形悬吊多摆的减振效率更高,但由于悬吊弹簧多摆可通过弹簧灵活调节刚度,因此其减振效果更佳。两种并联形悬吊双单摆由于两摆之间不具备耦合效应,控制性能和减振效果偏低,其减振效果与悬吊单摆的减振效果持平,但悬吊弹簧双单摆因其具有可灵活调节摆长、增大调谐频带、多阶振型调谐减振的能力,更适用于工程实际应用。

(2) 多层框架振动台试验进一步验证了各类悬吊摆对多层结构减振控制的有效性,悬吊弹簧双摆的减振效果最佳,且可以有效控制结构的前两阶周期。理论值与试验值结果较吻合,充分验证了本文提出的各悬吊摆数值分析动力学方程的合理性和精确性。

(3) 对于受多阶振型影响较明显的结构,两种串联形悬吊多摆的减振效果明显,在不考虑摆长限制的情况下,可优先选取。工程实际当中,悬吊弹簧双摆和悬吊弹簧双单摆因其更灵活的调节摆长能力,更适合应用于多高层减振控制中。综合考虑,悬吊弹簧双摆能灵活调节摆长解决工程受限问题、拓宽调谐频带、实现多阶调谐减振、减振效果最佳,在五种类型悬吊摆中,具有最佳的工程应用前景。

如何从机理上反映风攻角或双向地震作用下弹簧非线性刚度的问题,从而最大程度优化其调谐减振能力,仍需深入的研究。基于工程实际的摆长、质量块质量、弹簧刚度等参数优化设计也需要进一步开展。