基于高斯小波函数和线性表达法的开口板自由振动特性研究

郭文杰, 柴天建, 颜建伟, 洪 显

(华东交通大学 轨道交通基础设施性能检测与保障国家重点实验室,南昌 330013)

开口板是一种典型的工程结构形式,广泛应用于船舶、铁道、建筑、机械等领域,例如隐身舰船集成化上层建筑的设备口开孔[1]、轨道板开口内置钢弹簧浮置减振板[2]。开口板会引起动力学性能的变化,存在与开口附近设备产生共振的风险,还与向周围辐射的噪声有直接关系。开口尺寸、形状和边界条件是开口板振动特性影响的重要因素[3],因此研究开口板结构动力特性,对工程结构设计具有重要的实际意义。

针对开口板振动问题,主要有半解析法和数值方法[4-5]。数值方法主要为有限单元法,邱昌林等[6]采用有限元法研究了钢板开圆形口时的自振频率,张媛等利用有限元分析了不同开口尺寸对薄板自振频率的影响。传统能量法(如瑞利里兹法[7-9])在结构动力学中被广泛使用,它提供了一种快速而精确的方法来推导和求解给定系统的运动方程。例如Mundkur等[10]基于瑞利里兹法使用正交多项式函数分析了开口板的振动。Avalos等[11]应用Rayleigh-Ritz法对开两矩形口的矩形板进行计算,分析了不同大小、开口位置等对固有频率的影响。Larrondo等[12]应用Rayleigh-Ritz法对变厚度矩形多开口平板的自由振动进行分析,并对不同开口位置,开口大小对频率的影响进行分析。瑞利里兹方法依赖于位移形函数[13-14],形函数必须满足问题的各种约束条件。一些研究人员采用人工弹簧法[15-17]处理边界条件,将约束问题转变为无约束问题,例如:王旻昊等[18]采用人工弹簧法模拟边界条件,计算得到开口板的固有频率和响应振型,并讨论了开口尺寸和边界条件对自振特性的影响;张俊等采用人工弹簧模型模拟不同的边界条件。位移容许函数会影响求解精度和准确性,改进傅里叶级数法[19]可以克服传统傅里叶级数在边界处不连续线性,可以适应结构的一般边界条件。例如:邱永康等[20]利用改进傅里叶级数方法作为开口板位移场的形函数,分别研究了复杂边界条件下单开口和多开口矩形板的自振特性;Shi等[21]应用改进的傅里叶级数方法对一般边界条件下多个矩形开口的矩形板的自由振动特性进行了分析,计算了内部开口和外部开口的固有频率,并得出了振型图。

人工弹簧-瑞利里兹法,将有边界约束问题转化为无约束问题,对于边界约束的处理具有相当的优点。人工弹簧-瑞利里兹法是一类有参数方法,模型的收敛性在很大程度上取决于弹簧刚度的值。弹簧刚度越大,高阶模式的收敛性越好,但当弹簧刚度取值过大时可能导致矩阵奇异问题[22]。此外,形函数的选择也是影响瑞利里兹法求解精度的关键因素。现有研究中常采用的位移形函数有切比雪夫多项式级数[23]等和改进傅里叶级数作为全局性函数,在计算非开口板或厚度连续变化板时具有较好的收敛性,但在计算非连续变化板厚的开口板时,则需要更多的级数项才能满足计算精度。

本文以能量法为基本框架,采用线性表达法(linear expression method,LEM)来处理各种边界条件,将有边界约束问题转变为无约束问题。基本思路是通过高斯消元法找到约束条件矩阵中线性无关的列向量,将位移形函数的未知系数转变为线性无关系数列向量的线性表达,从而将有约束问题转变为无约束问题;根据能量法基本原理,构建了拉格朗日能量泛函,并对位移形函数的系数进行变分求极值,将振动问题转化成求解特征值和特征向量的问题。与人工弹簧法相比,不需要设置弹簧刚度等参数,避免了矩阵可能奇异的问题。选取高斯小波函数[24-25]作为开口板的位移形函数,以确保能够准确捕捉开口位置处的局部化特征。以四边简支和四边固定的开口板为例进行分析,结合有限元方法计算结果,讨论解的收敛性和准确性。研究了不同开口尺寸、形状对自振频率的影响。计算了不同边界约束条件下多开口板的自振频率。线性表达法使用简便,编程快捷,可广泛应用于有约束问题分析中。

1 理论分析

1.1 开口矩形板的力学模型

本文以矩形薄板中心开圆孔为具体研究对象,以中点为坐标原点建立直角坐标系,如图1所示。板长2a,宽2b,厚度h。定义边界条件表示符号如下:固定边界C,简支边界S,自由边界F,从左侧开始,逆时针顺序表示四边边界约束。例如:SFSF表示左右边简支,上下边自由;SSSS表示四边自由。

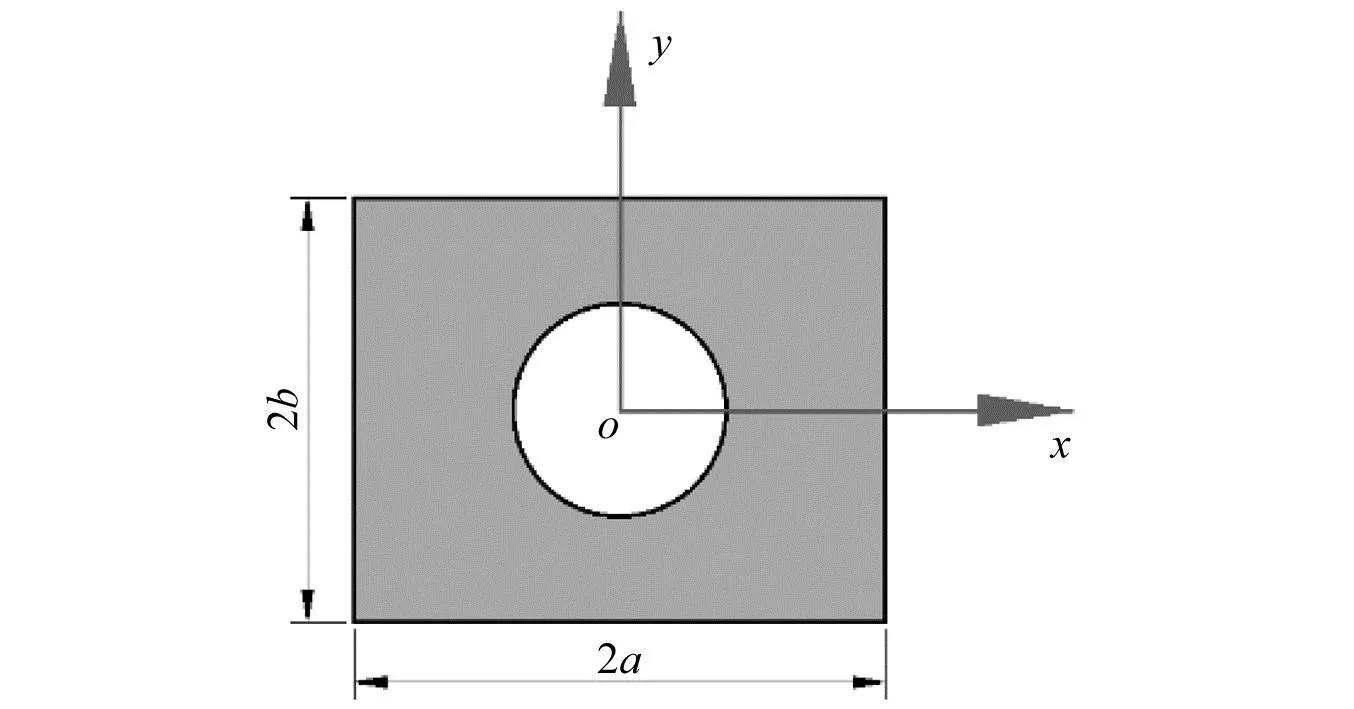
图1 矩形开口板示意图Fig.1 Schematic diagram of rectangular open plate

1.2 位移形函数

假设离面位移w表示为基函数ξi(x,y)和一组权重系数dk(t)的组合,即

w(x,y,t)=dTξ(x,y)

(1)

其中,

ξ(x,y)=φ(x)⊗ψ(y),
φ=[φ1(x),φ2(x),…,φi(x),…,φm(x)]T,
ψ=[ψ1(y),ψ2(y),…,ψi(y),…,ψn(y)]T

式中: ⊗为克罗内克积;φ为x方向的容许梁函数;ψ为y方向的容许梁函数。

针对开口板厚度局部突变,本文采用具有局域化特性的高斯小波函数描述位移形函数[26-27],以捕捉厚度变化区域的波动特征。据此,基函数φi(x)、ψi(y)表示为

(2)

式中:p、q为x和y方向的伸缩因子;k、r为平移因子。

本节以x方向形函数φi(x)为例,对高斯小波函数式(2)分析。如图2所示,当平移因子k=0时,高斯小波函数的支撑范围为[-4×2-p, 4×2p],伸缩因子p取值越大,支撑范围越小,函数的分辨率越高[28-29]。为使函数支撑范围分辨率满足结构的尺寸要求,伸缩因子需满足式(3)的限制条件。

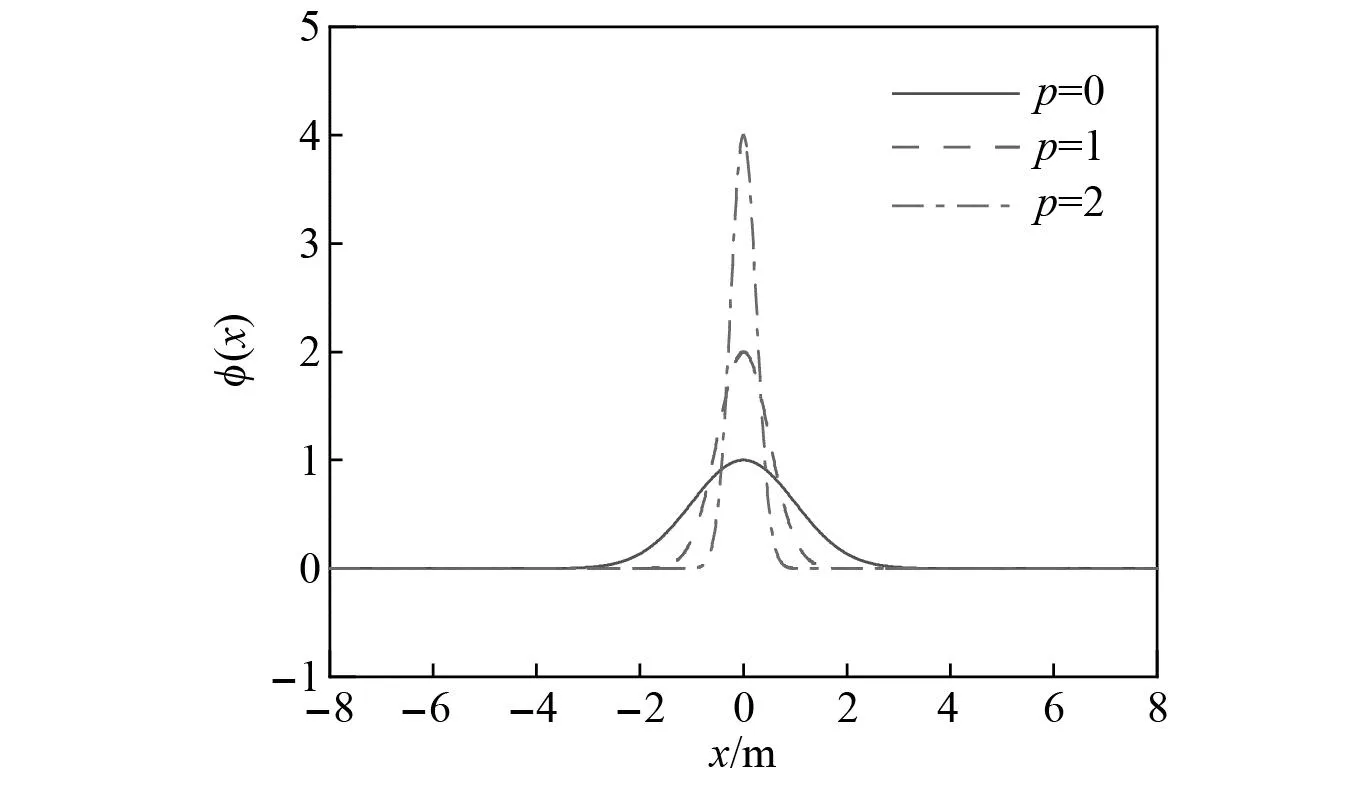
图2 不同伸缩因子对应的高斯曲线Fig.2 Gaussian curves corresponding to different scaling factors

(3)

式中, ceil(·)为向上取整数。

图3所示,当p=0时,高斯小波函数的支撑范围为[-4+k,4+k],随着平移因子增大,支撑范围从左侧移到右侧。为使函数支撑范围覆盖结构的尺寸,平移因子需满足式(4)的限制条件。

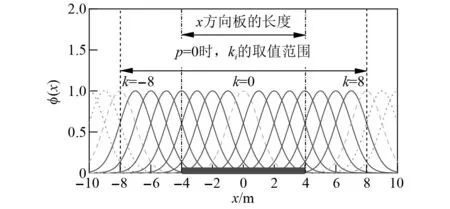
图3 不同平移因子对应的高斯曲线Fig.3 Gaussian curves corresponding to different translation factors

(4)

式中, floor(·)为向下取整数。

1.3 运动方程的建立

根据Kirchhoff-Love薄板理论,开口板的弯曲应变能为

(5)

令

式中:D=(Eh3)/[12(1-μ2)],E和μ分别为薄板材料弹性模量和泊松比;K为整体结构应变能的刚度矩阵。

厚度函数h(x,y)为

(6)

式中:p(x0,y0)为图1所示开口板坐标系内任意一点的横坐标和纵坐标;S为圆孔开口区域。

开口板的动能为

(7)

式中:ρ为薄板材料的密度;M为整体结构的质量矩阵。

整体结构的能量泛函可表示为

(8)

1.4 利用线性表达法考虑边界条件

四边简支开口板的边界条件如下

w(x,y,t)|x=±a=0,w(x,y,t)|y=±b=0

(9)

式(9)意味着形函数(1)中的权重系数d并非是独立的,而是存在线性相关性。

传统的能量法,通常采用构造满足位移边界条件的位移函数w(x,y)[30],将自由振动的二阶微分方程问题转化为特征值和特征向量的求解。传统能量法的关键是构造合适的位移函数w(x,y),而对于一些边界条件的假设位移函数如自由边界则具有相当的难度。本文提出线性表达方法,将边界约束条件和位移函数分离,因此基函数的选择具有高度自由性。

将边界约束条件式(9)代入形函数式(1)中得到

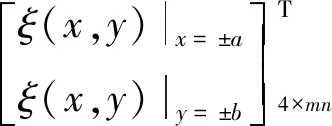
(10)

令

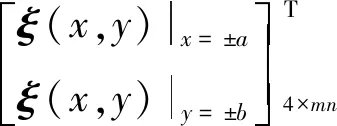
本文采用高斯消元法将约束矩阵转化为阶梯型矩阵,得到线性无关的列向量,即独立的权重系数。将未知系数中的线性相关系数由线性无关系数线性表达。

具体过程是,首先对G使用高斯消元法,形成简化的行阶梯形矩阵H。初等行变换不会影响解的结果,所以Gd=0和Hd=0是等价的。其次采用列变换将H矩阵中每行首个为1的列向量变换到前M列,变换后矩阵为F

F=HIrow

(11)

F=[PQ]

(12)

由于H矩阵的列位置发生了变换,d向量的行也要进行相应变换,变换后矩阵

γ=Irowd

(13)

得到变换后的向量为γ,将γ向量拆分为两部分,前M行为α向量,后(mn-M)行为β矩阵。

(14)

因为

Hd=HIrowIrowd=Fγ

(15)

所以Gd=0和Fγ=0是等效的,Gd=0可拆成两部分相加

P·α+Q·β=0

(16)

因为P矩阵是可逆的,故α可以由β线性表示

α=P-1·Q·β=0

(17)

结合式(13)、式(14)可得

(18)

式中,I为(mn-M)维的单位矩阵。将式(18)进行变换,便能将d由β表示。

(19)

令

则有

d=Z·β

(20)

将式(16)代入式(8),得到总能量泛函

(21)

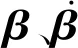
(22)

由于d是与时间相关的未知系数,定义与时间相关的未知系数β(t)=αeiωt,ω为振动的圆频率。特征方程可根据式(19)写出

(23)

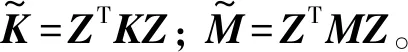
2 收敛性与准确性验证

本章进行收敛性和精度分析。以钢材为例,密度ρ=7 850 kg/m3,泊松比μ=0.3,弹性模量E=210 GPa;矩形板长2a=0.5 m,宽2b=0.4 m,圆孔半径r=0.1 m,厚h=0.005 m。根据式(3),伸缩因子满足p≥4,q≥5时解是收敛的。不失一般性,将x、y方向的伸缩因子取相同值,p=q。分析SSSS边界条件下的固有频率随伸缩因子变化关系。

当p=q=1时,低阶固有频率能收敛至解析解,当p=q=5,高阶固有频率也能收敛至解析解,如表1所示。

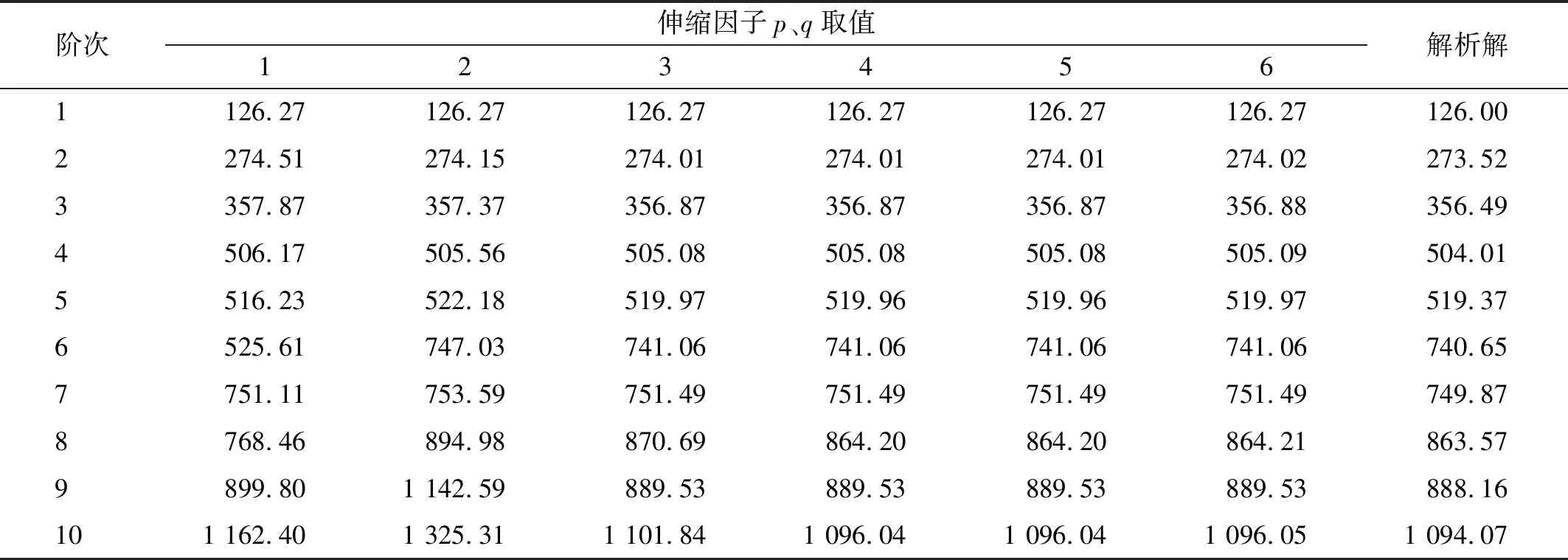
表1 未开口板固有频率随伸缩因子变化Tab.1 The natural frequency of an unopened plate varies with the expansion factor 单位:Hz

当p=q=5时,固有频率达到收敛,证明了式(3)的合理性,如表2所示。

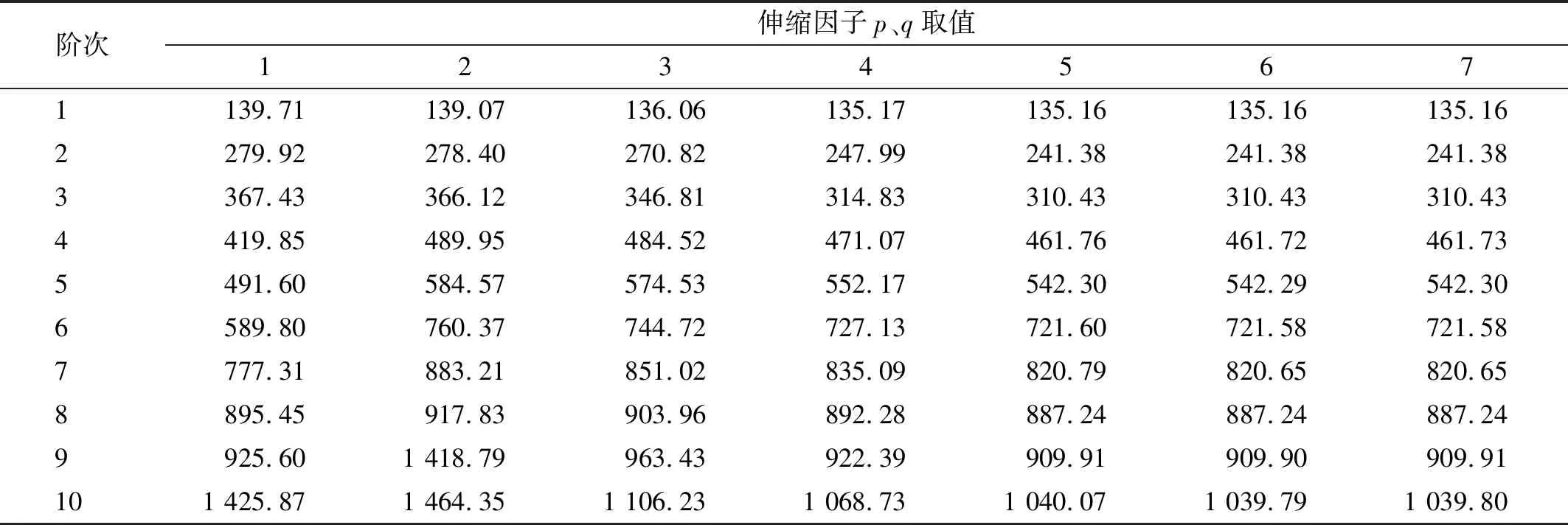
表2 开口板固有频率随伸缩因子变化Tab.2 The natural frequency of an open plate varies with the expansion factor 单位:Hz

以SSSS和CCCC边界条件下的开圆口的矩形板为例,进行准确性验证。圆形开口半径为r=0.1 m。将线性表达方法计算结果与有限元(finite element method,FEM)结果进行对比。采用的有限元软件为COMSOL,单元类型为板,结果如表3和表4所示。误差计算公式为

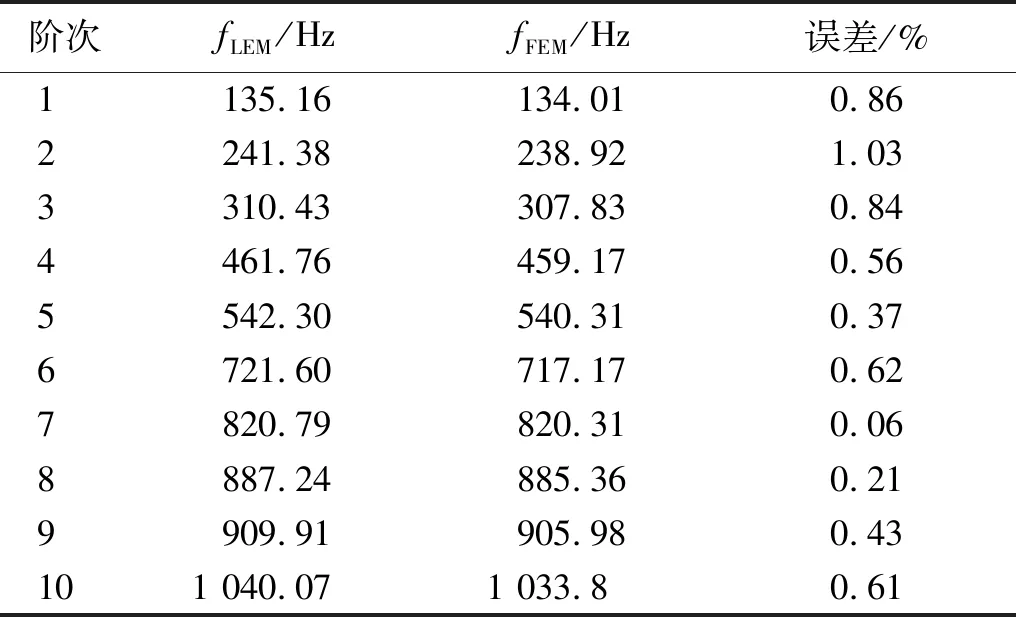
表3 SSSS边界下开圆口矩形板固有频率对比

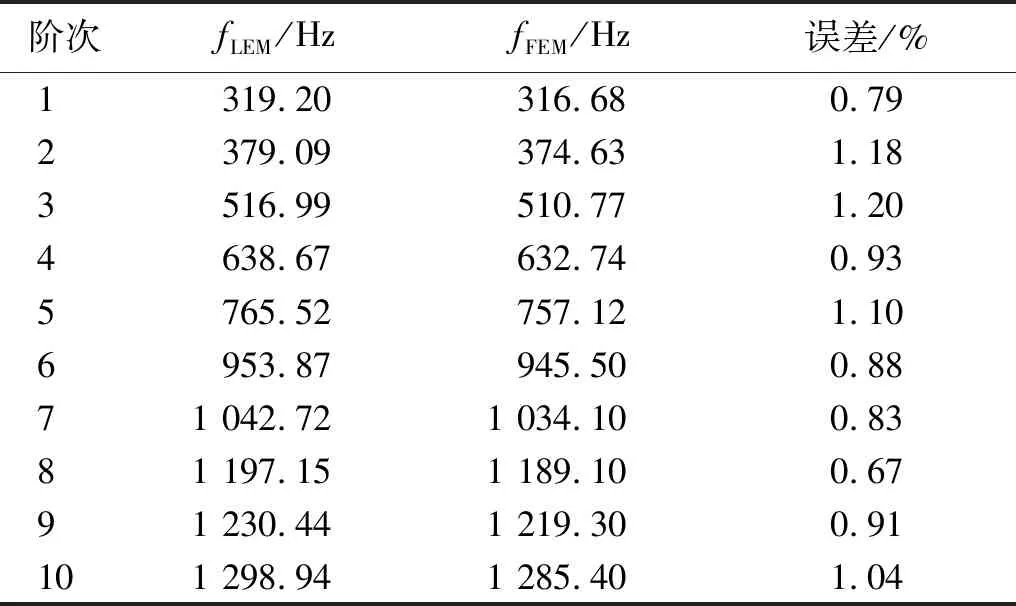
表4 CCCC边界下开矩形口矩形板固有频率对比

(24)

式中:fLEM为线性表示方法的结果;fFEM为有限元计算结果。

为了验证振型模态图的准确性, SSSS边界条件下LEM和FEM绘制的模态图,如图4所示。LEM与FEM得到的固有频率吻合良好,最大误差不超过2%,见表3、表4。LEM与FEM得到的振型图基本一致,见图4。综合固有频率和振型图的对比,说明LEM具有较高的准确性。

图4 SSSS边界开矩形口板模态图Fig.4 Modal diagram of SSSS boundary plate with rectangular opening

3 开口尺寸对振动性能的影响

为研究开口尺寸对开口板自振特性的影响,采用LEM对不同开口尺寸薄板的自振频率进行计算,分析开口尺寸对自振频率的影响规律。

在CCCC和SFSF边界条件下,研究开口半径r与开口板自振频率f的关系。矩形板长2a=0.5 m,宽2b=0.4 m,厚h=0.005 m;圆孔中心与板中心重合,开口半径从r=0(无开口),0.005 m、0.010 m、0.001 5 m、…、0.150 m。最大开口半径为0.15 m,当开口尺寸继续增大,薄板理论不再适用。将开口半径与固有频率关系绘制成图,如图5所示。

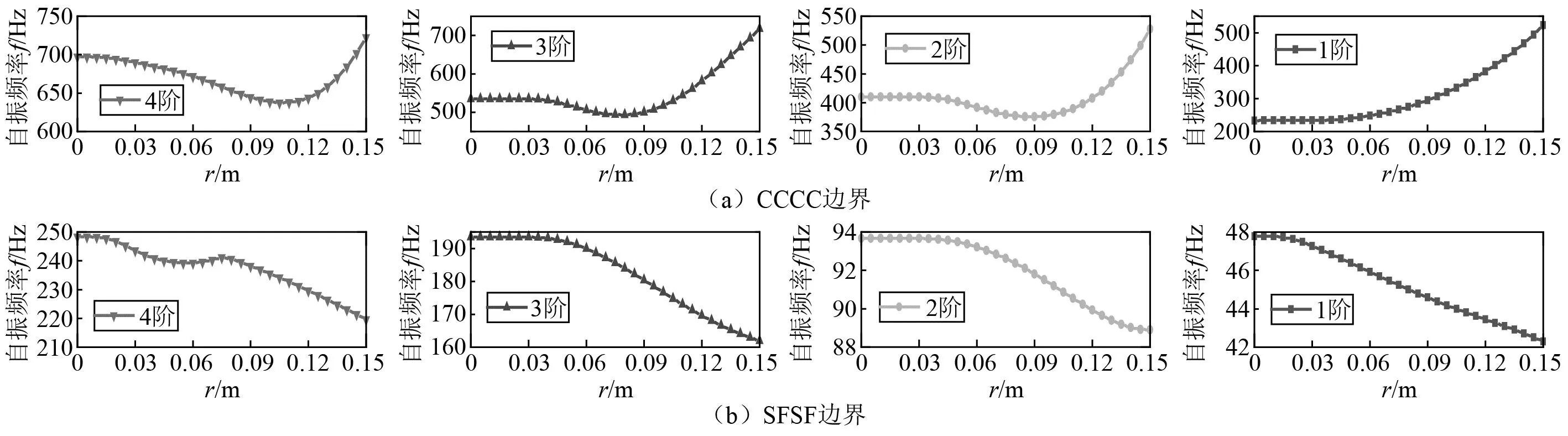
图5 不同边界下开口半径与固有频率关系Fig.5 Relationship between opening radius and natural frequency under different boundaries

由图5可知,当开口尺寸较小时,开口对各阶固有频率的影响较小。可能的解释是,固有频率和结构的动能和应变能有关,其中动能与结构的质量和速度相关,应变能与结构刚度有关。当开口较小时,对质量和刚度影响都较小,所以对固有频率的影响较小。小开口板的频率和模态可近似为未开口板进行分析。

在CCCC边界条件下,1阶固有频率随着开口尺寸增大而增大,2阶、3阶、4阶固有频率随着开口增大先减小后增大,见图5(a)。根据未开口矩形板振型图6,可能的解释是,在1阶振型中,中心开口位于振动峰谷位置,开口对动能影响比应对变能影响大,从而导致1阶固有频率随着开口尺寸增大而增大。2阶、3阶、4阶振型中,中心开口位于节线位置,开口对动能影响比应对变能影响小;随着开口尺寸增大,逐渐接近峰谷位置,对动能影响比应对变能影响大,从而导致固有频率随着开口增大先减小后增大。

在SFSF边界条件下,1～4阶固有频率随着开口增大而减小,见图5(b)。根据未开口矩形板振型图7,并与CCCC边界条件下进行对比,可能的解释是:1阶振型中,振动峰谷为一带状区域,不完全集中在中心位置,中心开口对动能影响比应对变能影响小;SFSF边界下整体刚度比CCCC边界下小,随着开口增大,对动能影响一直比应对变能影响小,没有出现CCCC边界下固有频率随着开口增大先减小后增大现象。

4 开口形状对振动性能的影响

为研究开口形状对自振特性的影响。采用LEM对不同开口形状薄板的自振频率进行计算,分析开口形状对自振频率的影响规律。

在CCCC和SSSS边界条件下,矩形板长2a=0.5 m,宽2b=0.4 m,厚h=0.005 m,开口面积s=0.02 m2,矩形孔长宽比a′/b′=ka,椭圆孔长轴与短轴比r1/r2=kr。不同长宽比ka、长短轴比kr与自振频率关系如图8、图9所示。

图8 CCCC边界下长短轴比kr与自振频率关系Fig.8 Relationship between the long to short axis ratio kr and natural frequency under CCCC boundary

图9 SSSS边界下长宽比ka与自振频率关系Fig.9 Relationship between aspect ratio ka and natural frequency under SSSS boundary

由图8、图9可知,在边界条件和开口面积相同情况下,开口形状对1阶、4阶自振频率影响较小(为1%～3%),对2阶、3阶影响较大(为8%～20%)。根据未开口矩形板振型图6,可能的解释是:1阶、4阶峰谷沿x轴和y轴对称,开口长边方向x轴和沿y轴对薄板的动能影响较接近;而2阶、3阶峰谷只沿y轴或只沿x对称,开口长边方向对动能的影响差异较大。

随着长宽比ka、长短轴比kr从0.5增大到2.0,1阶自振频率先增大后减小,2阶频率逐渐减小,3阶频率逐渐增大。可能原因是,当开口接近峰谷时自振频率增加,开口远离峰谷时自振频率减小。

5 多开口自振频率计算

以不同开口数量的矩形板为例,与有限元结果对比,验证LEM计算多开口板时的准确性。单元矩形板长0.5 m,宽0.4 m,厚0.005 m,圆孔半径0.05 m。开两孔模型如图10(a)所示,圆孔中心坐标为(±0.125,0);开四孔模型如图10(b)所示,圆孔中心坐标为(±0.125,±0.10);计算结果如表5和表6所示。

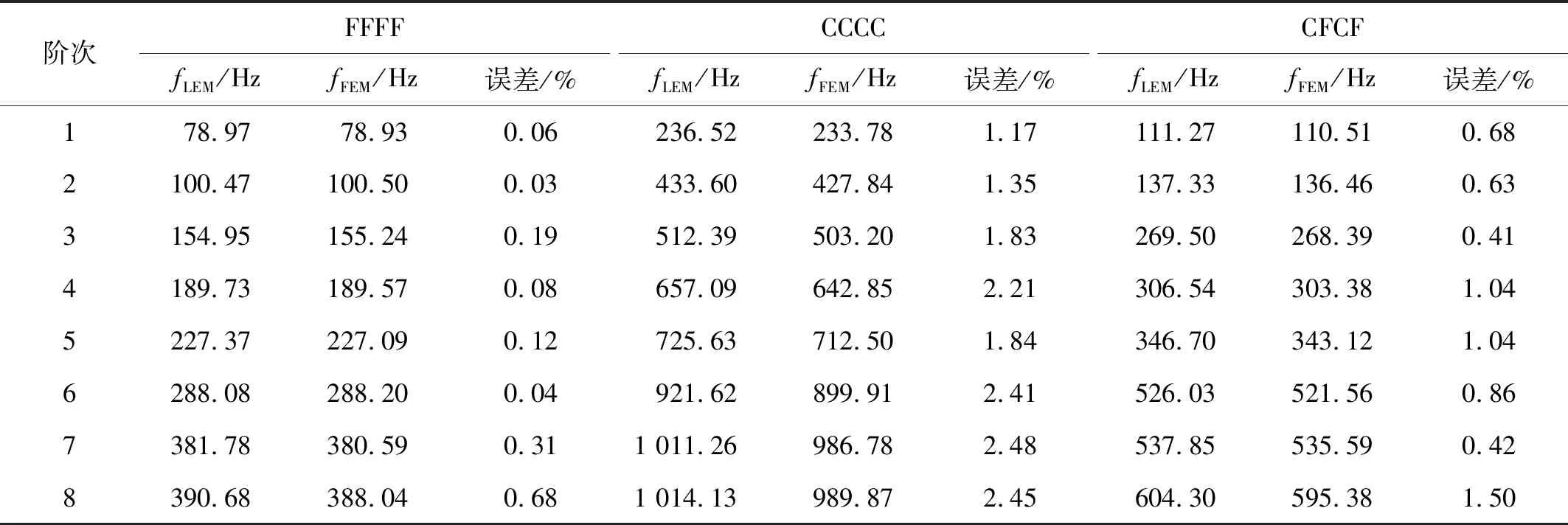
表5 不同边界下开两圆孔矩形板固有频率Tab.5 Natural frequencies of rectangular plates with 2 circular holes under different boundaries

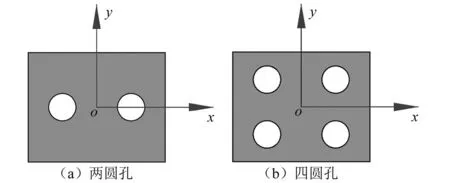
图10 多开口矩形板示意图Fig.10 Schematic diagram of multi opening rectangular plate

由表5、表6可知:在不同边界条件下,低阶固有频率误差基本在1%以内;在CCCC边界下,高阶固有频率最大误差小于2.5%,高阶固有频率误差大于低阶误差[31]。LEM在计算多开口矩形板自振频率准确可靠。

6 结 论

基于能量法原理,采用高斯小波函数作为位移函数,提出利用线性表达方法(LEM)处理边界条件,解耦了边界条件与位移形函数。首先以四边简支条件下开圆口薄板为例验证了LEM的收敛性和准确性,然后分析不同开口尺寸和不同开口形状下开口薄板的自振频率,最后分析了多开口矩形板自振频率。通过本文的研究,得到如下结论:

(1) 高斯小波函数中伸缩因子的取值与解的收敛性相关,当函数支撑范围小于板的边长时才能保证解收敛。

(2) 采用线性表达方法的不同边界条件下单开口、多开口振动计算结果与有限元计算结果吻合较好。

(3) 当开口尺寸较小时,开口对固有频率的影响较小,小开口板的频率和模态可近似为未开口板进行分析。开口对各阶自振频率影响程度随着模态图的峰谷位置变化。

(4) 在边界条件和开口面积相同情况下,随着开口形状与模态图中峰谷重合范围的不同,自振频率产生不同影响。