新型3D负泊松比多孔材料胞元的弹性性能研究
邓先溥,班宝旺,郄彦辉
(1. 河北工业大学 机械工程学院,天津 300130; 2. 唐钢国际工程技术有限公司,河北唐山 063000)
由于良好的能量吸收和抗冲击特性,多孔材料在汽车和航空航天领域得到了广泛应用[1-2]。负泊松比多孔材料也称为拉胀多孔材料,相比传统多孔材料,其具有更高的能量吸收和抗冲击能力,更高的剪切模量和压痕阻力,更强的断裂韧性等[3-5]。负泊松比多孔材料在工程领域具有广泛的应用前景,但其应用也存在很多有挑战性的科学问题[6-7],国内外学者对其展开了广泛研究。
1982年,Gibson等[8]发现内凹六边形具有负泊松比特性,实现了平面负泊松比多孔材料的人工设计。在此基础上,相关学者提出了内凹三角形、星型、双箭头形、手性结构等平面负泊松比多孔材料的胞元结构。1987年,Lakes[9]在Science上首次报道了利用聚氨酯泡沫制造的空间负泊松比多孔材料,开启了多孔材料空间负泊松比胞元结构的研究。Shokri等[10]将两个正交内凹六边形在内凹点拼接在一起形成多孔材料的空间负泊松比胞元,并利用能量法研究了该胞元的力学性能参数。Carneiro等[11]将两个正交的内凹六边形在直边中点拼接,得到了一种新的空间胞元。Li等[12]建立了一种有4个内凹面的负泊松比空间胞元,探究了由该胞元形成的夹芯板的屈曲行为。Yang等[13]制造并测试了一组空间负泊松比结构,证明了负泊松比特性越强,结构比吸能越大。Gao等[14]将两个内凹三角形结构进行正交组合得到了一种空间负泊松比胞元,并描述了胞元变形过程的力学特性。Yang等[15]设计了一种每个面由8个对称的“z”形杆组成的正方体状空间负泊松比多孔材料的胞元结构,并研究了杆件夹角和长径比对胞元力学性能的影响。Wang等[16]设计了一种空间的交叉手性负泊松比多孔材料,并分析了该材料在准静态和动态压缩下的力学性能和能量吸收性能。Beharic等[17]比较了内凹空间胞元、BBC格架和octet-truss点阵3种多孔材料组成的夹芯板结构在低速冲击下的性能,结果表明内凹空间胞元组成的夹芯板结构具有最佳的能量吸收特性。Qi等[18]基于内凹和手性特性设计了3种新型多孔材料的空间负泊松比手性胞元,并对其力学性能和变形机理进行了讨论。虽然对空间负泊松比胞元结构的设计、制造和力学性能研究取得较大进展,但是具有正交各向同性的空间负泊松比胞元结构还不多见,保持负泊松比特性不变条件下的弹性模量增强方案设计还有待开发。
在二维胞元的基础上,通过对内凹六边形的组合,设计了一种3个正交方向均具有负泊松比特性的新型空间胞元,并可通过三向、双向和单向增强方案实现正交各向同性或正交各向异性的强韧化设计。利用均匀化有限元方法和周期性边界条件研究了增强杆夹角等几何参数对胞元无量纲弹性模量和泊松比的影响。同时对该胞元结构进行了弹性压缩实验,以验证有限元模拟结果的正确性。
1 结构设计和几何参数
本文设计的新型正交各向同性3D负泊松比胞元(REC)如图1a)所示。其在x、y、z这3个方向的投影完全相同,均是相同尺寸和形状的内凹六边形,由于对称性,该胞元呈正交各向同性。当REC在单一方向上增强,可得到x-REC、y-REC、z-REC这3种单向增强胞元;单向增强胞元其增强方向与两个非增强方向间呈正交各向异性,两个非增强方向间则呈正交各向同性。REC在两个方向同时增强可得到xy-REC、yz-REC、zx-REC这3种双向增强胞元;双向增强胞元的增强方向与非增强方向呈正交各向异性,而两个增强方向间则呈正交各向同性。REC在3个方向上同时增强,得到具有正交各向同性特性的三向增强xyz-REC胞元。各增强胞元分别如图1b)~图1h)所示。
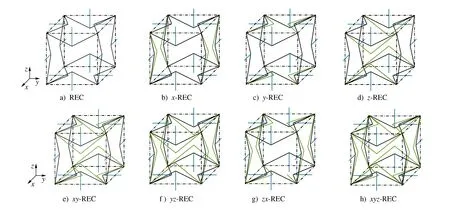
图1 新型空间负泊松比胞元和7种增强胞元Fig. 1 Novel spatial negative poisson′s ratio cell and 7 kinds of enhanced cells
由于结构的相似性,各胞元的几何参数示意图不再一一给出,以xyz-REC胞元为例,其平面几何参数示意图,如图2所示。该示意图在x、y、z方向上具有轮换对称性。
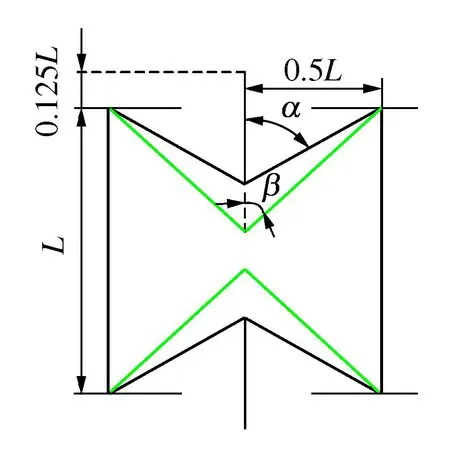
图2 胞元xyz-REC投影面几何参数示意图Fig. 2 Schematic diagram of geometric parameters of xyz-REC cell projection surface
图2中:L为胞元虚接正方体的边长,α为胞元内凹杆和连接杆的夹角;β为胞元增强杆和连接杆延长线的夹角。另外定义胞元各杆件正方形横截面的边长为b。考虑到胞元各构件间几何干涉的影响,参数的取值为:45°<α<90°、45°<β<α。为了结构的稳定性,令连接杆超出正方体胞元的部分为0.125L。
2 弹性性能的有限元研究
2.1 边界条件和材料参数
采用ANSYS Workbench19.1对各胞元结构进行有限元计算,研究几何参数对胞元力学性能的影响规律。使用编号BEAM189的二次单元对胞元进行网格划分,此单元基于Timoshenko梁理论,可以在考虑挠度和截面转角的同时计算梁单元在两个方向的弯曲,计算更精确。通过对有限元网格进行收敛性和精确性分析,确定梁单元长度为1 mm。材料为高韧性树脂,其弹性模量E=2 665 MPa,泊松比υ=0.38,密度ρ=1 150 kg/m3。
在计算中将胞元z向连接杆下端点设定为固定支撑,z向连接杆上端点加载压力F=20 N,研究几何参数对胞元力学性能的影响。
2.2 胞元等效长度L的影响
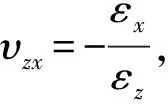
生活中,磁场无处不在,无论是手机,还是手提包上的磁扣都会产生磁场。磁场会对机械表的运作产生干扰,因此,保持机械腕表走时精准稳定,一枚防磁机心是必需的。那么,15,000高斯强磁场的威力究竟有多大?
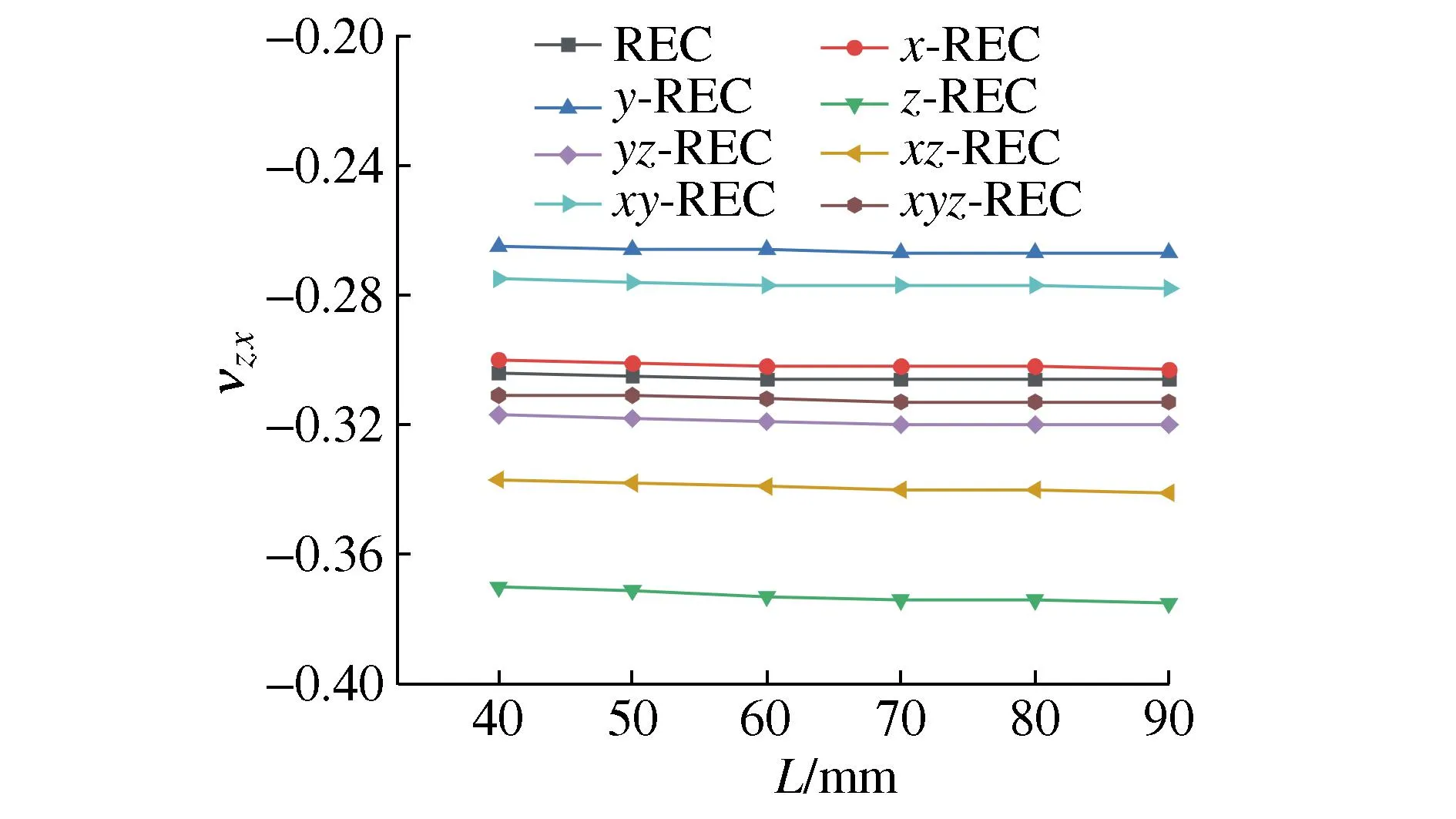
图3 L对υzx的影响Fig. 3 Effect of L on the υzx
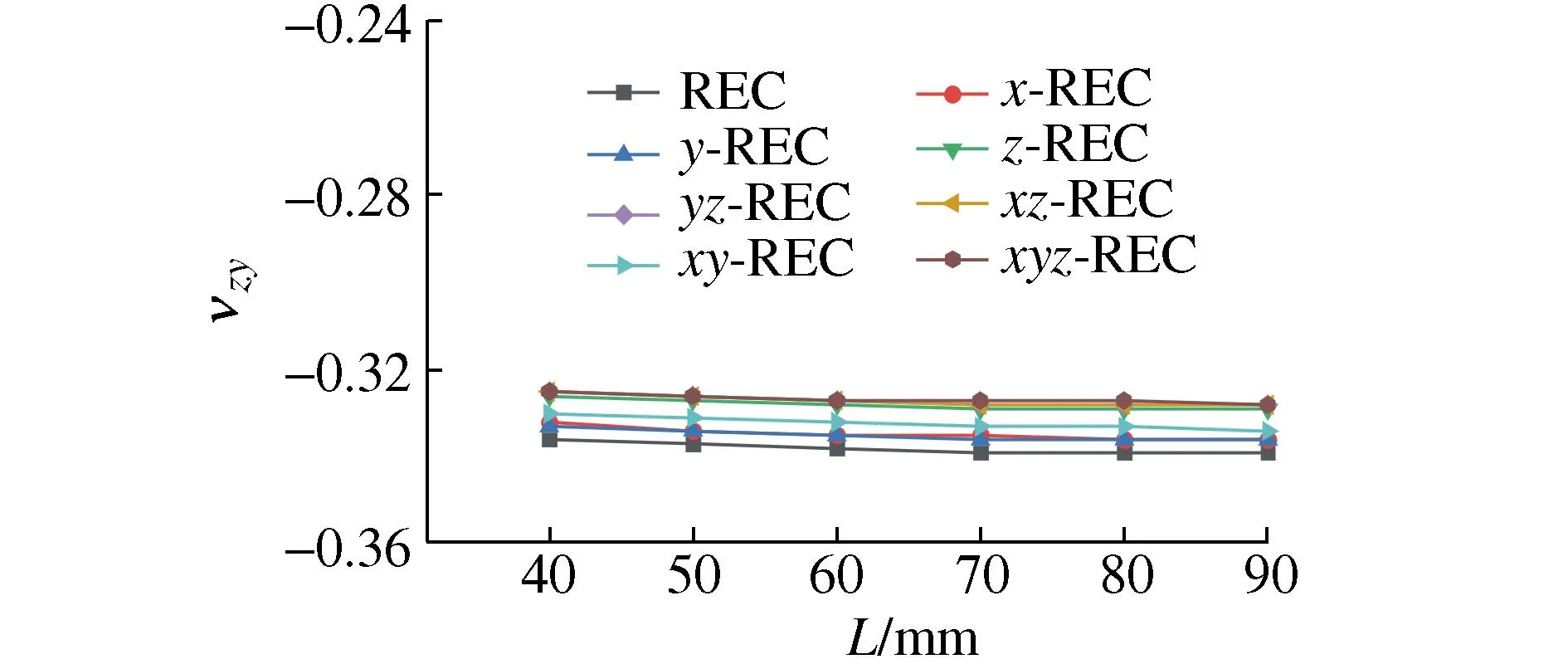
图4 L对υzy的影响Fig. 4 Effect of L on the υzy
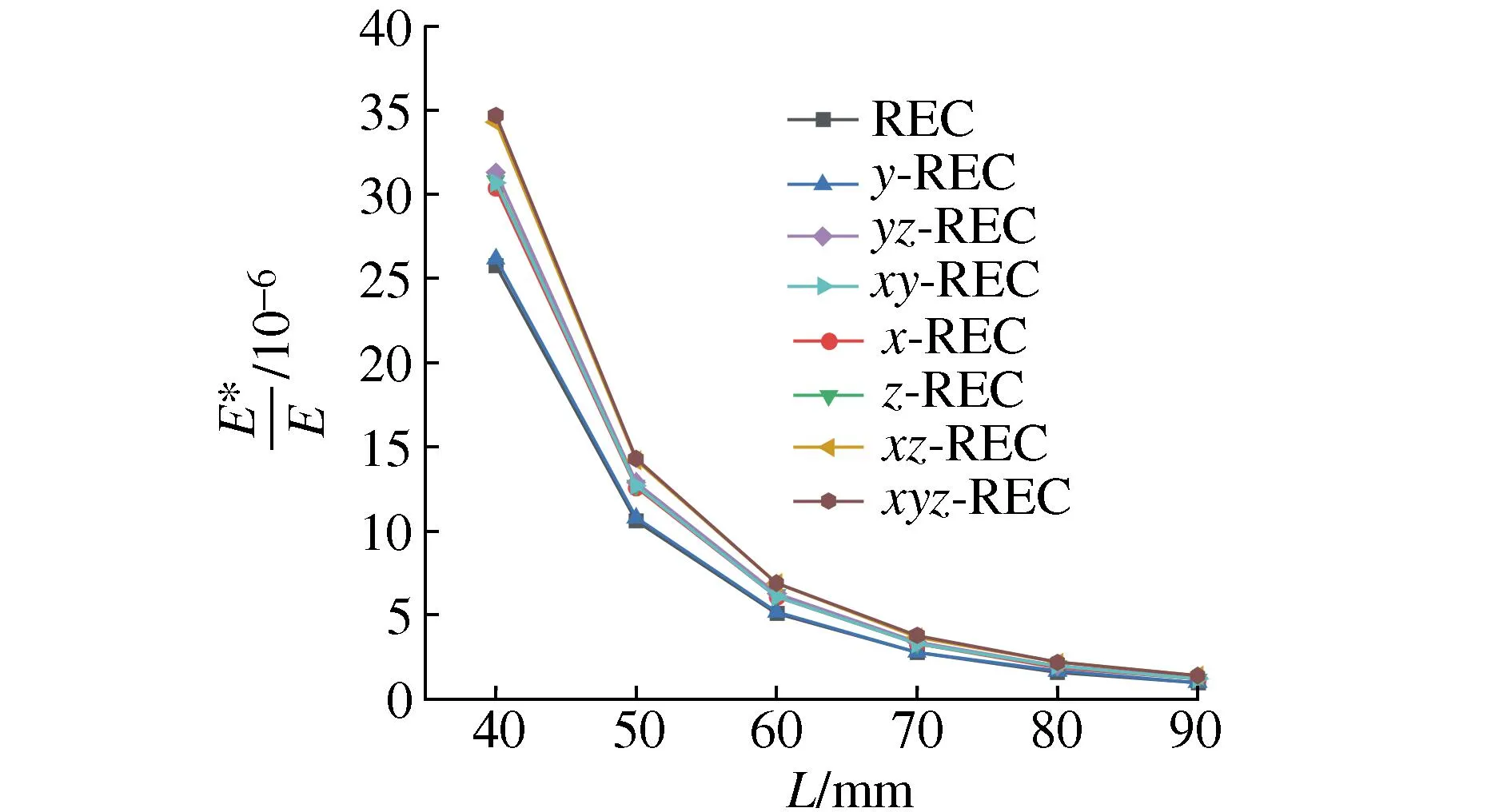
图5 L对E*/E的影响Fig. 5 Effect of L on the E*/E
图3和图4分别为各胞元zx和zy向泊松比随变量L的变化关系,可以看出8种胞元zx和zy向的泊松比基本保持不变,不随L变化,即zx和zy向负泊松比特性不受L影响。
由图3可知:8种胞元泊松比υzx的范围为-0.265~-0.375之间,y-REC胞元的泊松比υzx最大,z-REC胞元的泊松比υzx最小。相较REC胞元,x-REC、y-REC和xy-REC这3种胞元的υzx分别提升了1.3%、12.7%、9.5%;即x向、y向和xy双向这3种增强方案,会提高新型REC胞元zx向的泊松比υzx(降低胞元zx向的负泊松比特性)。相较REC胞元,z-REC、xz-REC、yz-REC、xyz-REC这4种胞元的υzx分别减小了22.2%、11.1%、4.6%、2.3%。即z向、xz双向、yz双向、xyz三向这4种增强方案,会降低新型REC胞元zx向的泊松比υzx(增强胞元zx向的负泊松比特性)。
由图4可知:8种胞元zy向泊松比υzy的范围为-0.325~-0.339。xyz-REC胞元υzy最大,但其相对υzy最小的REC胞元zy向泊松比仅增大了3.5%,说明增强方案对新型胞元REC的zy向泊松比υzy影响较小。
图5为无量纲弹性模量E*/E随L的变化,可以看出8种胞元的无量纲弹性模量均随着L的增大而减小,但减小速率趋缓。在8种胞元的无量纲弹性模量曲线中,REC和y-REC胞元的两条曲线基本重合、数值最小;x-REC、z-REC、xy-REC和yz-REC胞元的4条曲线基本重合、数值居中;zx-REC和xyz-REC胞元的两条曲线基本重合、数值最大。说明xz双向和xyz三向增强方案对新型胞元无量纲弹性模量的提升效果更显著。
2.3 杆件截面边长b的影响
以杆件截面边长b为变量,当参数L=80 mm,α=70°,β=50°时,研究变量b对胞元泊松比和无量纲弹性模量的影响。
图6和图7分别为各胞元zx和zy方向泊松比随变量b的变化关系,可以看出各胞元zx向泊松比υzx和υzy不随b的变化而变化,各增强方案对胞元泊松比的影响规律和图3和图4一致。
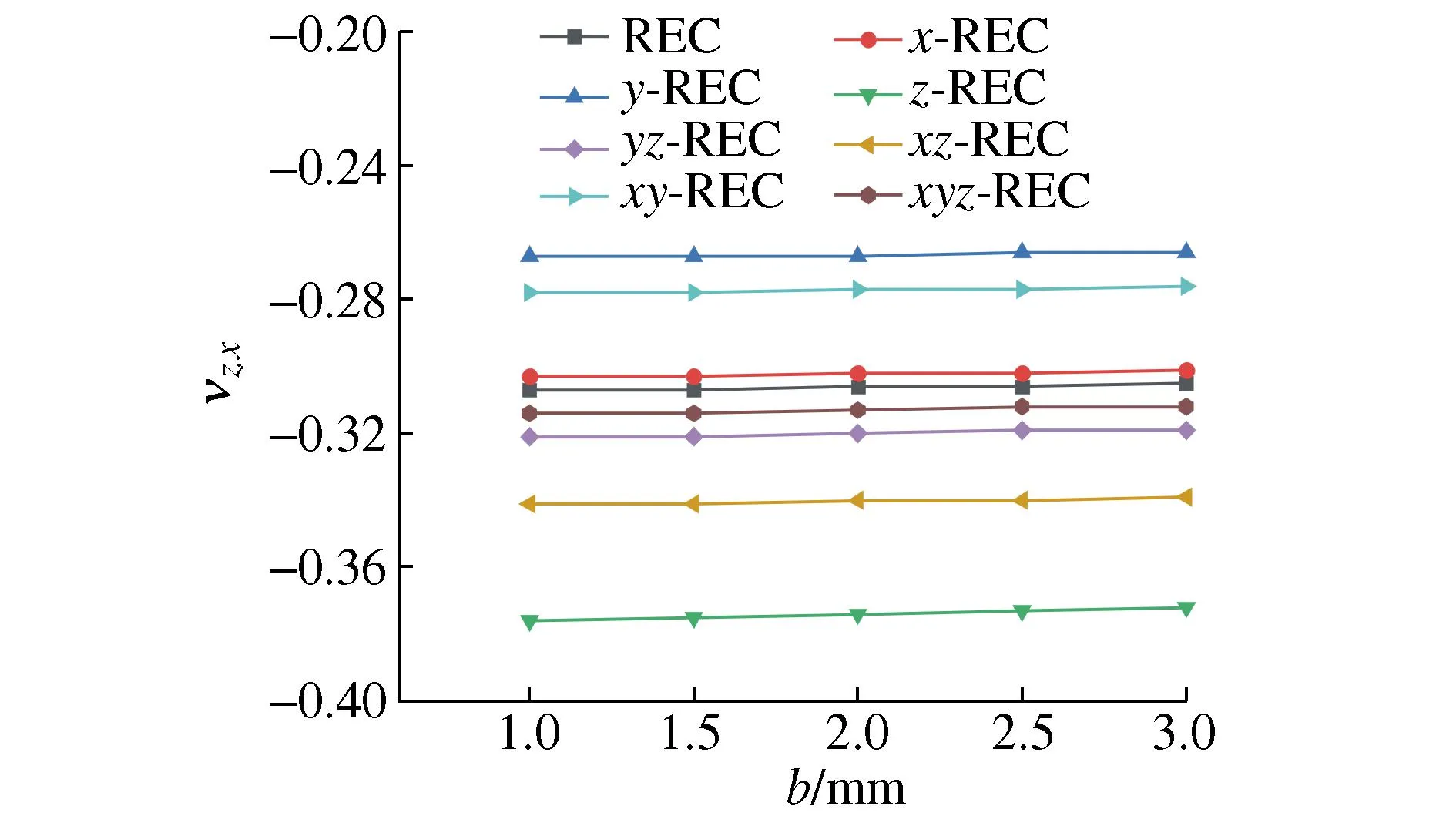
图6 b对于υzx的影响Fig. 6 Effect of b on the υzx
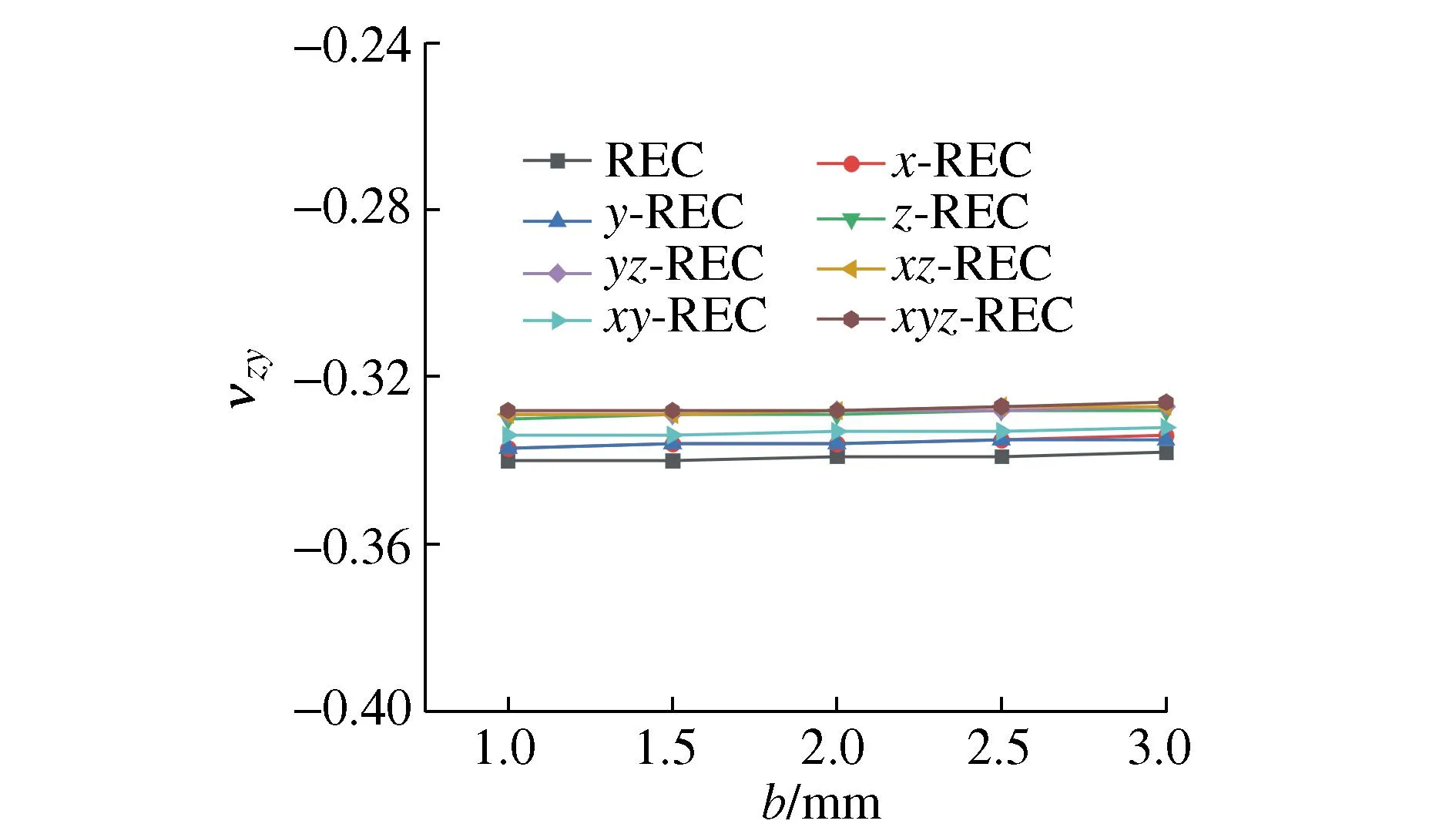
图7 b对于υzy的影响Fig. 7 Effect of b on the υzy
图8为各胞元无量纲弹性模量E*/E随b的变化关系,可以看出8种胞元的无量纲弹性模量均随b的增大而快速增大。由图8可知:xyz-REC和xz-REC两种胞元的无量纲弹性模量最大。在b=2.5 mm时,相较于胞元REC,xyz-REC和xz-REC两种胞元的E*/E数值分别增大了33.3%和34.8%。
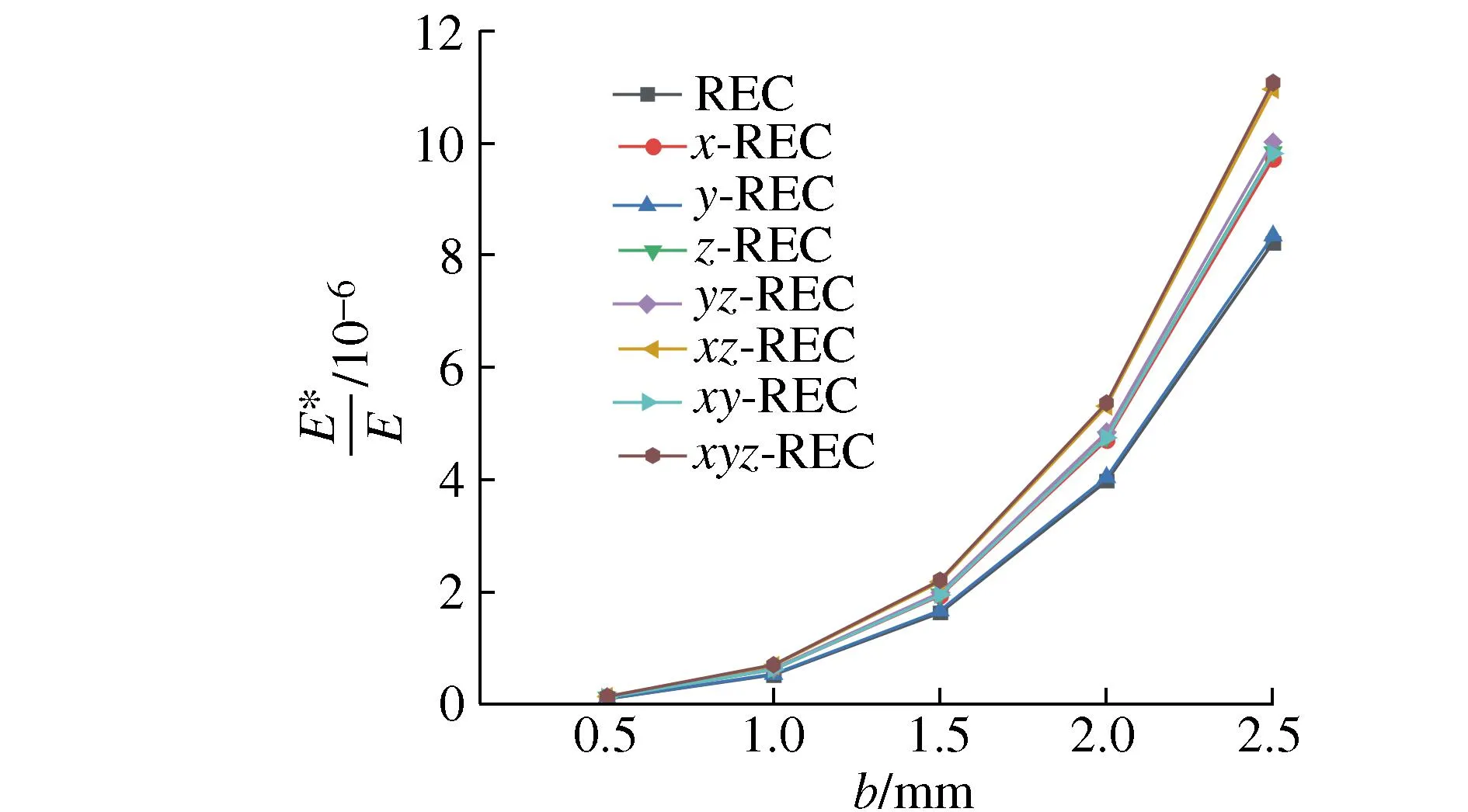
图8 b对E*/E的影响Fig. 8 Effect of b on the E*/E
2.4 内凹角α的影响
以内凹杆和连接杆的夹角α为变量,参数L=80 mm,β=50°,b=2 mm时,研究变量α对胞元泊松比和无量纲弹性模量的影响。
图9为各胞元zx向泊松比随α的变化关系。可以看出,除x-REC和xy-REC胞元外,其他胞元的zx向泊松比υzx与α基本呈线性增加关系。在整个α的取值范围内,z-REC胞元的zx向泊松比υzx均最小。而υzx取最大值的胞元则会发生变化,当55°≤α≤60°时,xy-REC胞元的zx向泊松比υzx最大;而当62.5°≤α≤70°时,y-REC胞元的zx向泊松比υzx最大。
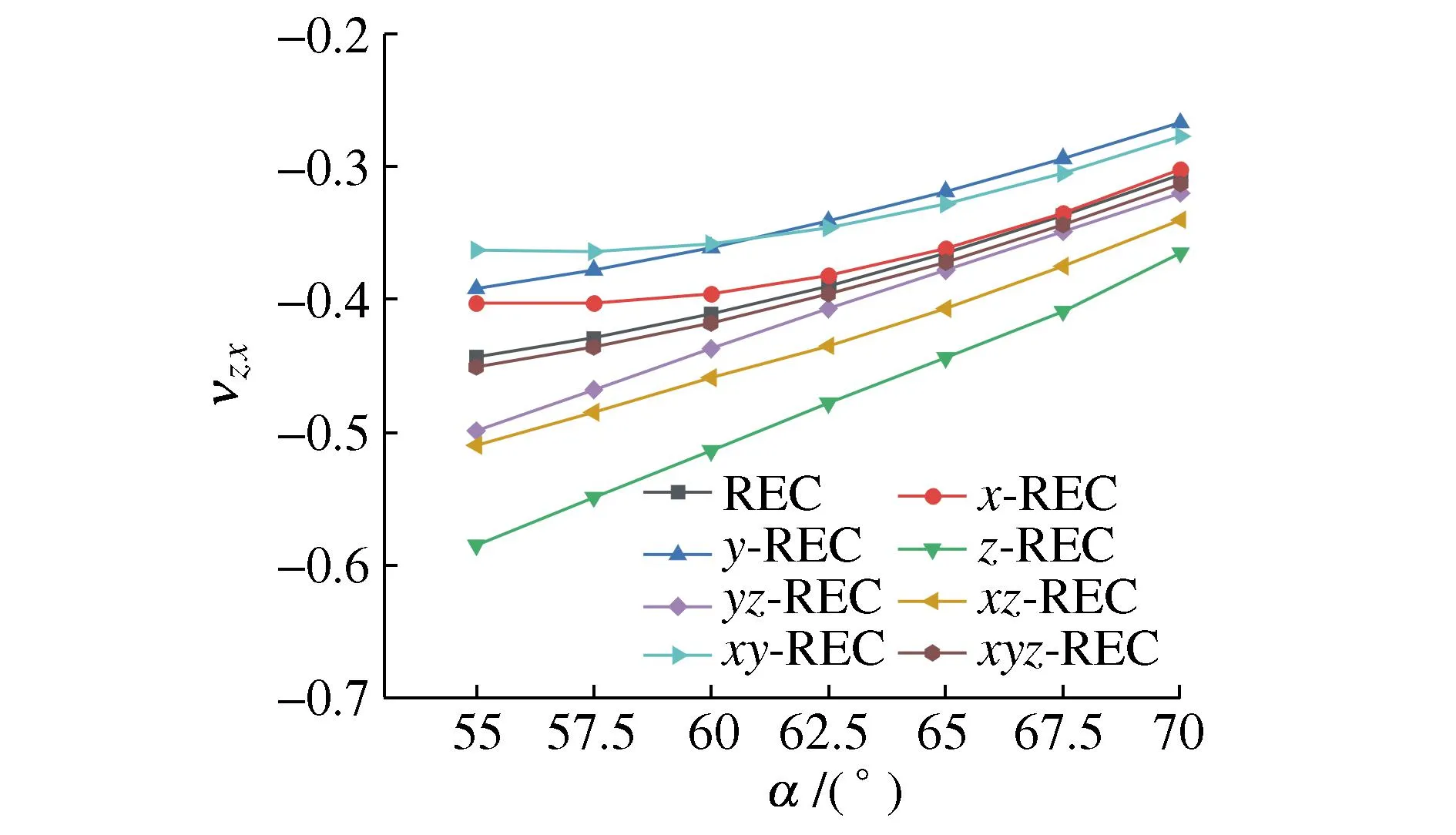
图9 α对υzx的影响Fig. 9 Effect of α on the υzx
相较于REC胞元,在α=55°时,z-REC、xz-REC、yz-REC和xyz-REC这4种胞元的zx向泊松比υzx分别降低了32.1%、15.1%、12.6%、1.8%,在α=70°时,则分别降低了19.3%、11.1%、4.6%、2.3%。
图10为各胞元zy方向泊松比随α的变化关系,可以看出随着内凹角α的增大,各胞元zy方向泊松比υzy也随之增大,即zy方向的负泊松比特性减弱。当α=55°时,相较于REC胞元,z-REC的υzy增加12.3%,而xy-REC胞元的υzy则减小6.5%。当α趋近70°时,8种胞元的zy向泊松比υzy趋于一致。
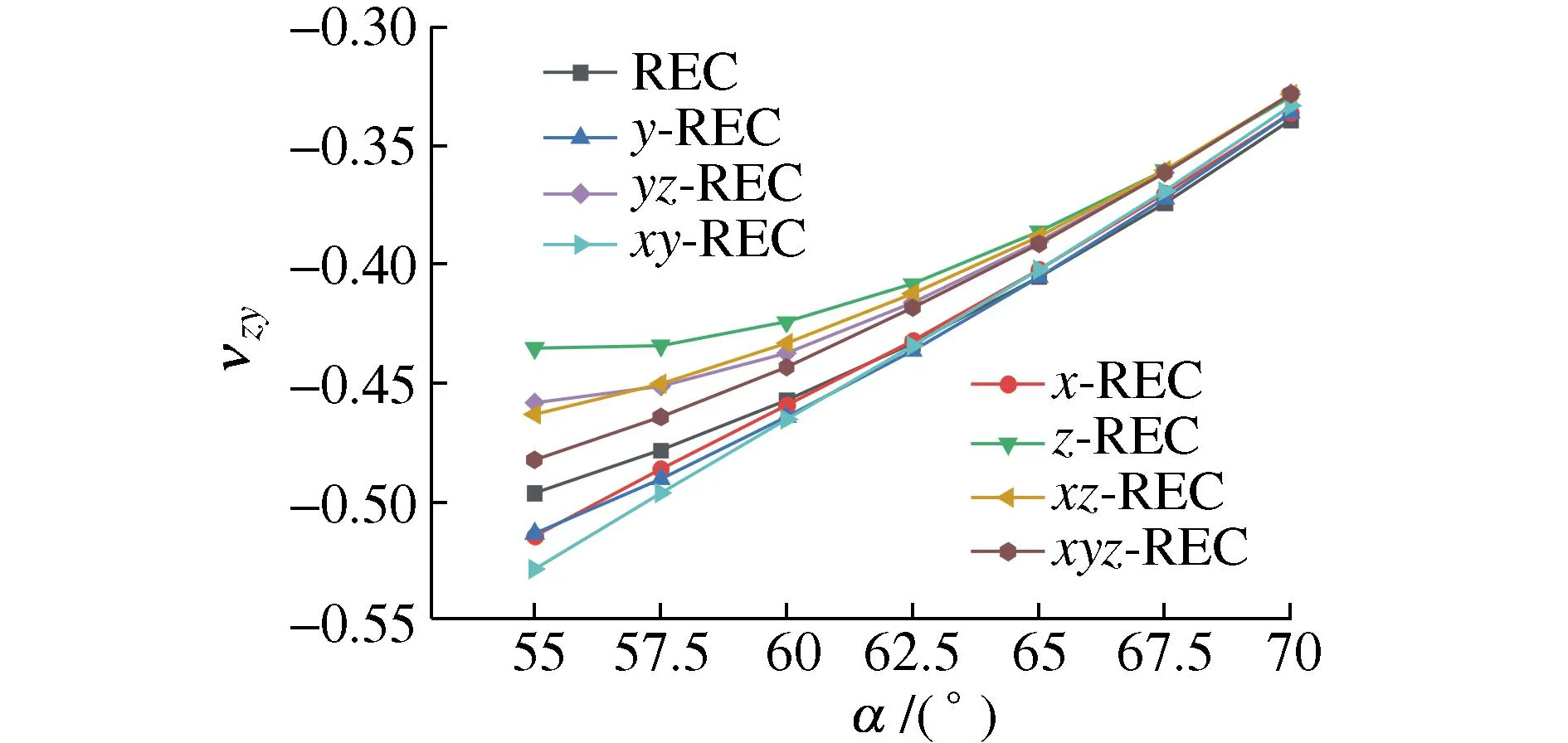
图10 α对υzy的影响Fig. 10 Effect of α on the υzy
图11为各胞元无量纲弹性模量E*/E随α的变化关系,可以看出,8种胞元的无量纲弹性模量均随内凹角α的增大而线性增加。7种增强方案都能提高新型空间胞元REC的无量纲弹性模量,xyz-REC受3个方向增强杆共同作用,提升效果最强,当α=55°时提升64.5%,α=70°时提升35.6%。
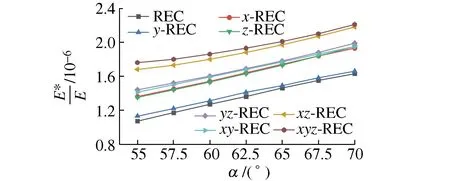
图11 α对E*/E的影响Fig. 11 Effect of α on the E*/E
2.5 增强杆内凹角β的影响
以内凹杆和连接杆延长线的夹角β为变量,参数L=80 mm,α=70°,b=2 mm时,研究变量β对胞元泊松比和无量纲弹性模量的影响。由于REC胞元不具有内部增强杆,所以在图中使用黑色虚线标示。
图12为各胞元zx向泊松比υzx随β的变化关系。可以看出,y-REC、xz-REC、y-REC这3种增强胞元的υzx随β线性变化,y-REC胞元的υzx线性增加、xyz-REC胞元的υzx保持不变、xz-REC胞元的υzx则线性减小。当β<55°时,x-REC、xy-REC、yz-REC、z-REC这4种增强胞元的υzx保持不变。当β>55°时,x-REC、xy-REC胞元的υzx增加,且增速变快;yz-REC、z-REC胞元的υzx降低,且降速也变快。
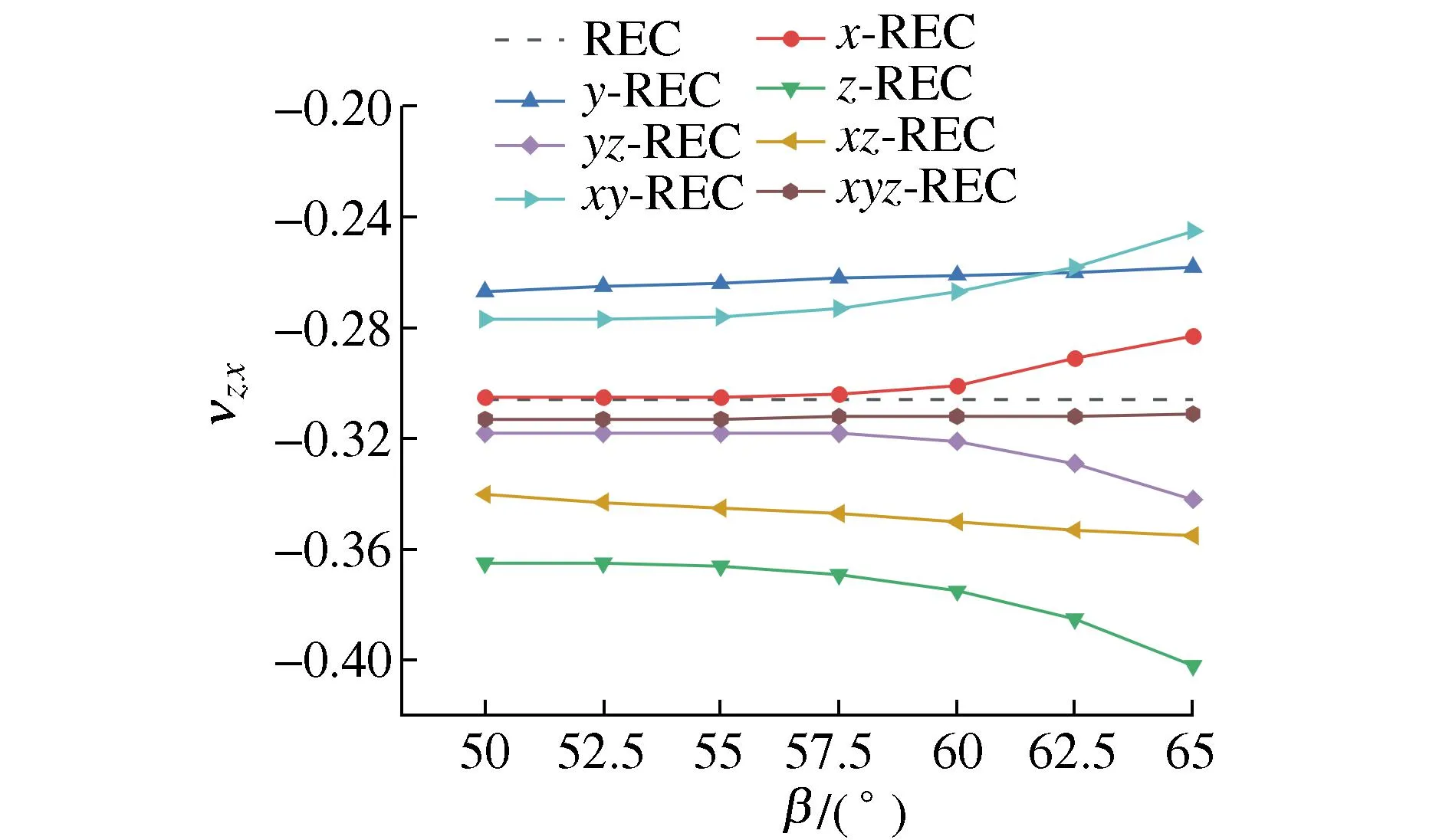
图12 β对υzx的影响Fig. 12 Effect of β on the υzx
由图13可知:随着增强杆内凹角β增大,各胞元zy向泊松比υzy几乎保持不变,即使在β=65°时υzy的数值变化也很小。这说明各胞元zy向负泊松比特性几乎不受β影响。
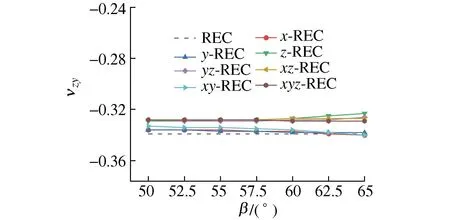
图13 β对υzy的影响Fig. 13 Effect of β on the υzy
图14为各胞元无量纲弹性模量E*/E随内凹角β的变化规律,可以看出随着β增加,z-REC、xz-REC、yz-REC和xyz-REC这4种增强胞元的无量纲弹性模量会缓慢增加,而其他胞元的无量纲弹性模量则基本保持不变。再一次说明7种增强方案均可提高新型空间胞元z方向的无量纲弹性模量,平行于载荷方向增强杆的引入是提高胞元无量纲弹性模量的有效方法。

图14 β对E*/E的影响Fig. 14 Effect of β on the E*/E
2.6 与已有文献胞元负泊松比性能对比
将z向增强胞元z-REC与文献[10-12]中由内凹六边形组成的空间结构胞元进行负泊松比特性对比。对比时,统一各胞元内凹角和边长,通过控制各胞元杆件横截面尺寸使各胞元的等效密度一致,z向加载,比较各胞元的zx向和zy向负泊松比,如图15和图16所示。
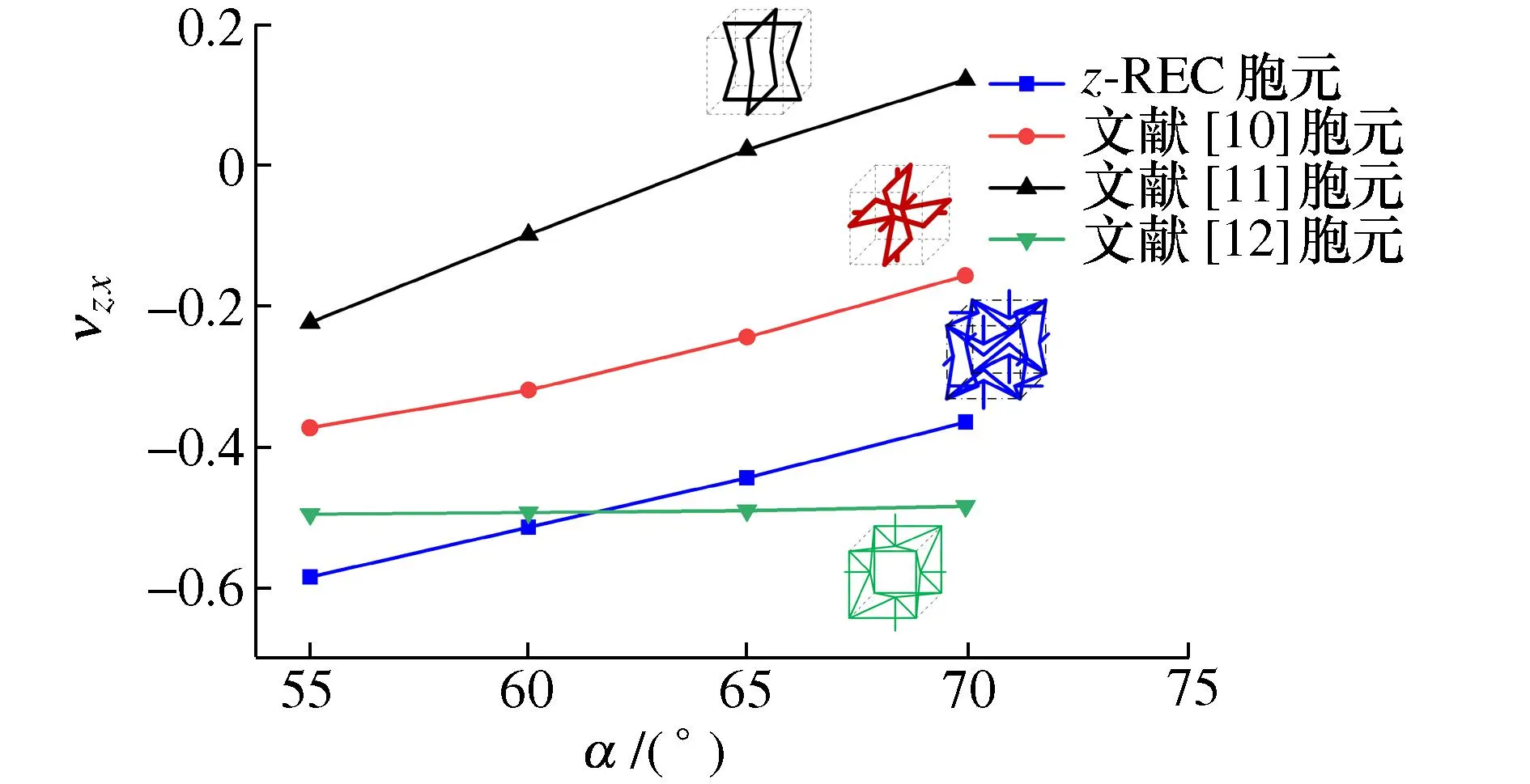
图15 胞元υzx对比Fig. 15 Comparison of each cell υzx
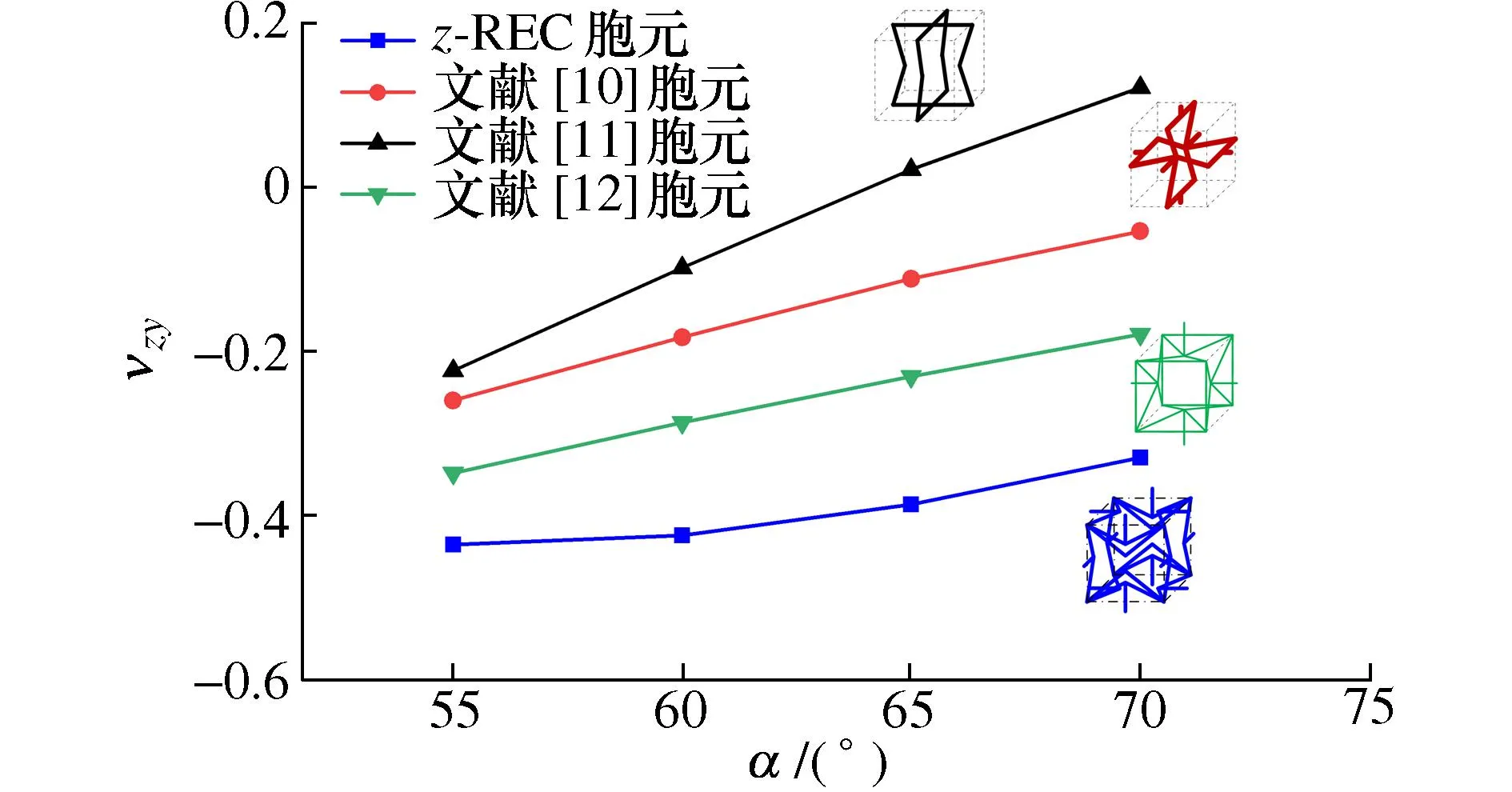
图16 胞元υzy对比Fig. 16 Comparison of each cell υzy
由图15可知:内凹角α≤60°时,z-REC胞元zx向负泊松比υzx最小,即zx向负泊松比特性最明显。内凹角α≥65°时,z-REC胞元υzx仅高于文献[12]胞元,也具有较好的负泊松比特性。由图16可知:z-REC胞元zy向负泊松比υzy最小,即其zy向负泊松比特性最明显。由此可知,z-REC胞元在垂直于加载方向上均具有较高的负泊松比特性。
2.7 讨论
不同几何参数引起胞元具有不同的力学性能指标,不同的增强方式还会导致增强胞元的正交各向异性和正交各向同性特性;在工程应用时可以根据实际工况的不同,选取不同的几何参数和增强方案。如为了获得较大弹性模量,在考虑成本的条件下,xz-REC相对xyz-REC更具优势。又如REC、x-REC、y-REC、xy-REC、xyz-REC的zx向泊松比υzx大于zy向泊松比υzy,其余结构则相反。
需要说明的是,与通常负泊松比胞元的弹性模量(无量纲弹性模量)增强方案会降低胞元负泊松比特性不同,REC胞元的z向、yz双向、xz双向和xyz三向4种增强方案,不仅会提高胞元在加载方向的无量纲弹性模量,还会提高结构zx向的负泊松比特性,这为高吸能多孔材料的高弹性模量设计提供了新思路。
值得注意的是,本文研究内容将胞元结构限制为正方体,若取消此限制,新结构可以获得更大的无量纲弹性模量和泊松比的取值范围。
3 实验验证
通过3D打印制备了一组试件,进行压缩实验,与有限元计算结果进行对比。试件使用材料为高韧性树脂,使用单轴试验机INSTRON3365,图17为试件实验加载图,实验所得数据和有限元计算数据对比如图18~图20所示。

图17 试件示例及实验图Fig. 17 Example of specimen and experimental diagram
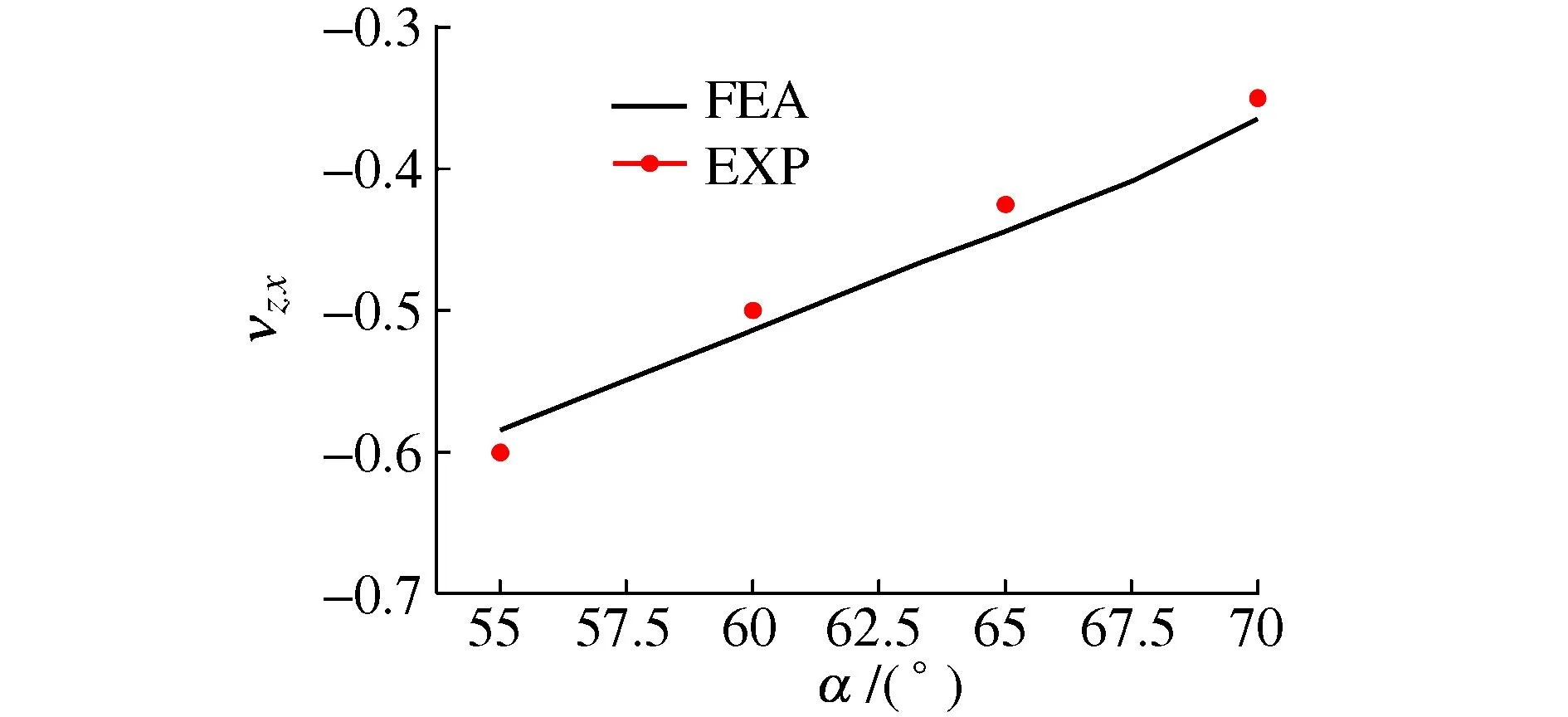
图18 实验和有限元υzx比较Fig. 18 Comparison of υzx between experimental results and FEM results
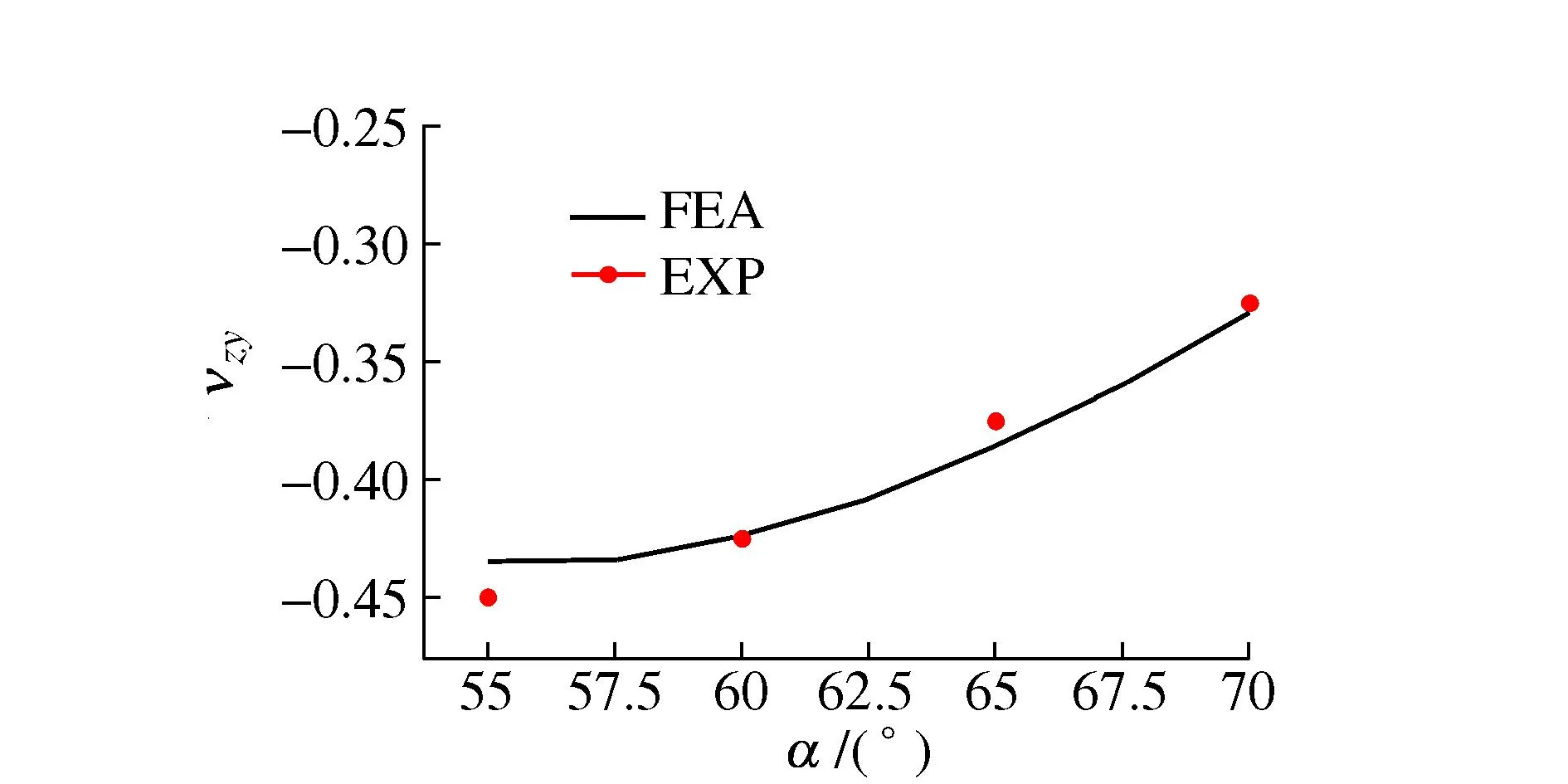
图19 实验和有限元υzy 比较Fig. 19 Comparison of υzy between experimental results and FEM results
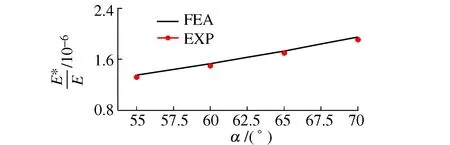
图20 实验和有限元E*/E比较Fig. 20 Comparison of E*/E between experimental results and FEM results
由图18~图20可知:实验数据和有限元数据拟合效果较好。图18中数据误差依次为2.5%、2.8%、4.5%、4.3%,图19中误差为3.3%、0.2%、2.9%、1.2%,图20中误差为2.3%、2.3%、1.7%、2.0%。误差主要源于3D试件制备有一定变形和测量误差。
4 结论
1) 所有胞元zx向泊松比υzx随内凹角α增大而增大;增强胞元则根据增强方案的不同,其zx向泊松比υzx随增强杆内凹角β的增大分别表现出增大、减小和不变3种趋势。所有胞元zy向泊松比υzy随内凹角α增大而增大,几乎不受增强杆内凹角β影响。
2) 胞元无量纲弹性模量随有效边长L增大而减小,随杆件横截面边长b增大而增大,随内凹角α增大近似呈线性增大,随增强杆内凹角β增大则呈现出不变和增大两种趋势。
3) 增强方式的不同会导致增强胞元具有不同的力学特性,单独对加载方向(z-REC)进行加强,结构的负泊松比效应最好,对3个方向(xyz-REC)同时加强,结构的弹性模量最大。通过灵活选择增强方案和几何参数,可以获得具有不同力学性能的空间负泊松比胞元结构。

