考虑多种失效模式耦合的复合材料损伤分析
何易周,张凝,尹硕辉
(湘潭大学 机械工程学院,湖南湘潭 411105)
与传统金属材料相比,复合材料更具优势,因此常被用于海上风电、航空航天等高科技领域。然而复合材料在其工作过程中,由于受到应力作用,导致复合材料发生损伤失效,其中损伤类型主要分为层合板损伤、界面脱黏失效、胶体裂纹扩展3种失效,最终导致载荷承载能力和密封性降低。因此,研究复合材料在工作过程中受到的损伤具有一定实际价值。
目前,采用有限元仿真是研究复合材料损伤问题的主要技术手段。Nagaraj等[1]提出一种由高阶理论开发的数值模型来模拟研究在低速冲击下层合板的损伤情况。郑亦媚等[2]通过Hashin失效准则和渐进损伤理论,建立了可以准确预测材料为玻璃纤维且含褶皱的复合材料层合板强度。张军等[3]确定了不同形状内聚力模型的适用范围。Rafiee等[4]运用CZM来研究黏结剂厚度和宽度对其失效的影响。龙文元等[5]运用XFEM模拟了复合材料断裂时的裂纹扩展行为。Santos等[6]对双塔接接头进行试验和数值模拟,通过试验结果与数值仿真结果的比较,发现XFEM能够准确预测双塔接接头的性能。冯威等[7]、周伟等[8]将XFEM与CZM二者结合,研究了胶体内部裂纹扩展路径以及板材与胶体分离的过程。
综上,国内外学者对复合材料损伤问题开展了一定的实验和数值仿真工作,但是大多数关于复合材料损伤失效的研究只考虑了一种失效模式,并未考虑多种失效模式的共同作用来对研究复合材料的损伤问题。因此,需要展开进一步的研究。本文先利用ABAQUS有限元仿真软件建立MMB有限元模型,并在此基础上探讨了层合板损伤、胶体裂纹扩展、界面脱黏3种损伤失效之间的内在联系,以及它们对复合材料力学性能的影响。
1 复合材料损伤分析基本理论
1.1 内聚力模型
在对裂纹问题的模拟过程中,由于CZM可以避免裂纹尖端的奇异性,因此CZM已经成为研究裂纹问题的强力手段,同时其适用范围较广,本文将利用CZM来模拟界面脱黏失效。双线性CZM[9]模型的本构关系如图1所示。

图1 双线性CZM张力位移关系Fig.1 Bilinear CZM traction displacement relationship
双线性CZM的方程表达式如下

(1)
式中:T为张力;δ为界面张开位移值;δf为界面失效位移值;δ0为界面分层损伤起始位移值;σmax为最大应力。
在复合材料工作过程中,由于受Ⅰ型、Ⅱ型和Ⅲ型多种损伤的影响,导致其应力状态较为复杂。在3种裂纹模式影响下,本文损伤起始准则采用二次应力准则来模拟内聚力单元失效,其表达式为

(2)
式中:tn、ts、tt依次分别为Ⅰ型、Ⅱ型和Ⅲ型下的应力;<>为Macaulay括号。
对于断裂能,常用幂定律和B-K准则定律来计算断裂能。
幂定律为
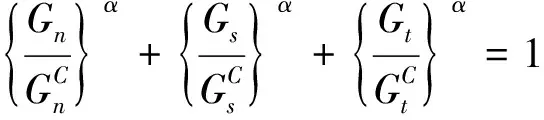
(3)
BK断裂准则为
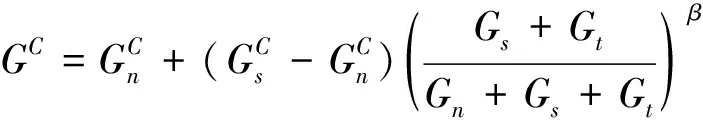
(4)
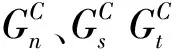
1.2 扩展有限元法
本文采用XFEM[10]模拟胶体裂纹扩展失效,XFEM与传统有限元相比较,XFEM的优势是不用对裂纹等缺陷进行网格划分,故常用XFEM来研究裂纹扩展问题。在计算过程中,需要选择裂纹初始准则,由于本文数值仿真中只需要用到最大主应力准则和最大主应变准则,因此对上述两种准则进行简单叙述。
最大主应力准则为
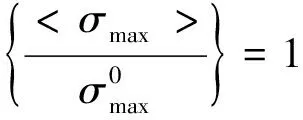
(5)
最大主应变准则为
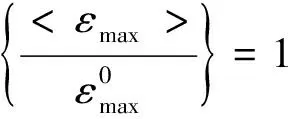
(6)

1.3 Hashin失效准则
本文利用ABAQUS里的USDFLD子程序建立了三维Hashin失效准则[11],其判定公式为:
(7)
式中:σij为应力,i=1,2,3,j=1,2,3;Sij为剪切强度,τij为切应力;XT、XC分别为纤维拉伸强度和压缩强度;YT、YC分别为基体拉伸强度和压缩强度;ZT、ZC分别为分层方向上的拉伸强度和压缩强度。
由于层合板的力学性能是会随着损伤程度的加深而出现退化,为模拟复合材料力学性能的退化,故通过定义材料参数退化方式[12-14]的方法来模拟复合材料的损伤过程。
2 混合型弯曲断裂有限元模型
根据实验[15]建立MMB有限元模型,几何模型如图2所示。MMB模型尺寸为102 mm×25.4 mm×6.24 mm,试件右端中间有一道裂纹,裂纹长度为34.1 mm,加载臂长42.2 mm。试件材料选择AS4/PEEK,AS4/PEEK的具体参数如表1所示。
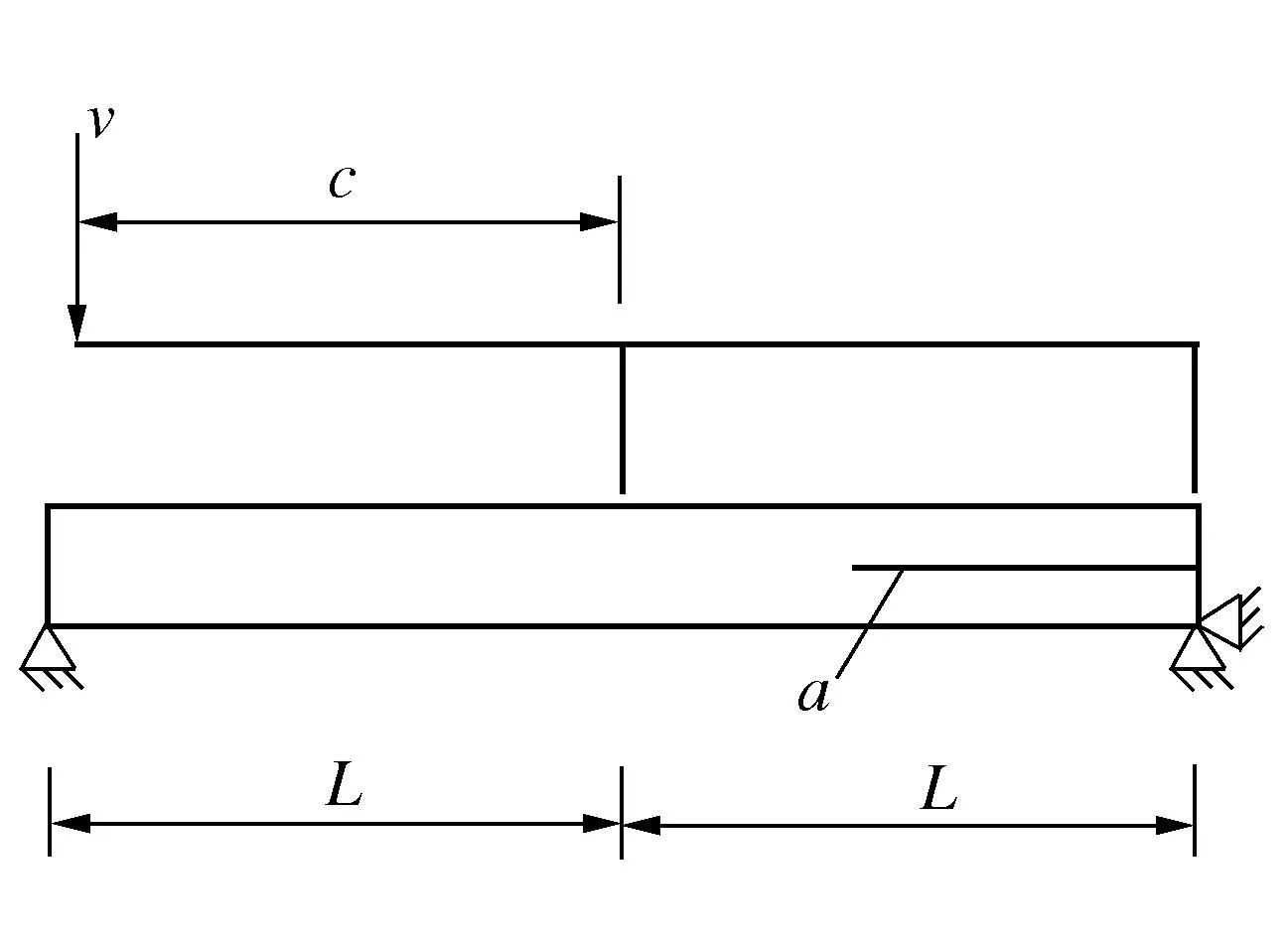
图2 MMB几何模型Fig.2 MMB geometric model

表1 AS4/PEEK材料属性Tab.1 AS4/PEEK material properties
MMB有限元网格模型如图3所示,其中网格为六面体网格,为了不影响结果的准确以及提高数值仿真计算效率,在加载臂与试件的接触表面进行较密的网格划分。

图3 有限元网格模型Fig.3 Finite element mesh model
图4为MMB模型实验过程的有限元模拟结果和实验数据比较,结果表明最大断裂载荷实验为275.35 N,数值仿真为290.88 N,误差为-5.64%。

图4 位移-载荷曲线图Fig.4 Displacement-load curve
从图4可以看出数值仿真结果与实验结果趋势一致,初步验证了MMB有限元模型的有效性。进一步验证了MMB有限元模型的有效性。
3 多失效模式损伤分析
3.1 层合板损伤-界面脱黏耦合失效数值模拟
为了探讨层合板损伤对界面脱黏的影响,对MMB模型的材料做了调整。整体尺寸102 mm×25.4 mm×6.24 mm。此处模型不考虑黏性层厚度,另外MMB模型中长度c=42.2 mm,裂纹长度a=34.1 mm。试件材料选择T300/1034-C,铺层顺序为[0/±45/902],铺层数量为5层,每层厚度为0.624 mm,总厚度为3.12 mm。T300/1034-C材料单层板参数如表2所示,层间参数同AS4/PEEK材料。

表2 T300/1034-C材料属性Tab.2 Material properties of T300/1034-C
不考虑黏性层厚度MMB有限元模型如图5所示,其边界每件同图2。为探讨层合板损伤与界面脱黏的内在联系,此处对MMB模型进行两组数值仿真计算,两组之间的区别在于有无考虑层合板损伤失效。另外在计算过程中,层合板损伤失效判定公式选择三维Hashin失效准则,内聚力模型的形状、损伤准则以及断裂能判定方式依次分别为双线性、二次应力准则以及BK断裂准则。

图5 忽略黏性层厚度MMB有限元模型Fig.5 MMB finite element model ignoring viscous layer thickness
未考虑层合板损伤失效的数值仿真结果如图6所示,考虑层合板损伤失效的数值仿真结果如图7所示。综合图6、图7分析,可以发现在试件模型尺寸、边界条件等一致的情况下,只考虑界面脱黏失效情况下裂纹长度比同时考虑层合板损伤和界面脱黏两种失效模式耦合下裂纹长度大。
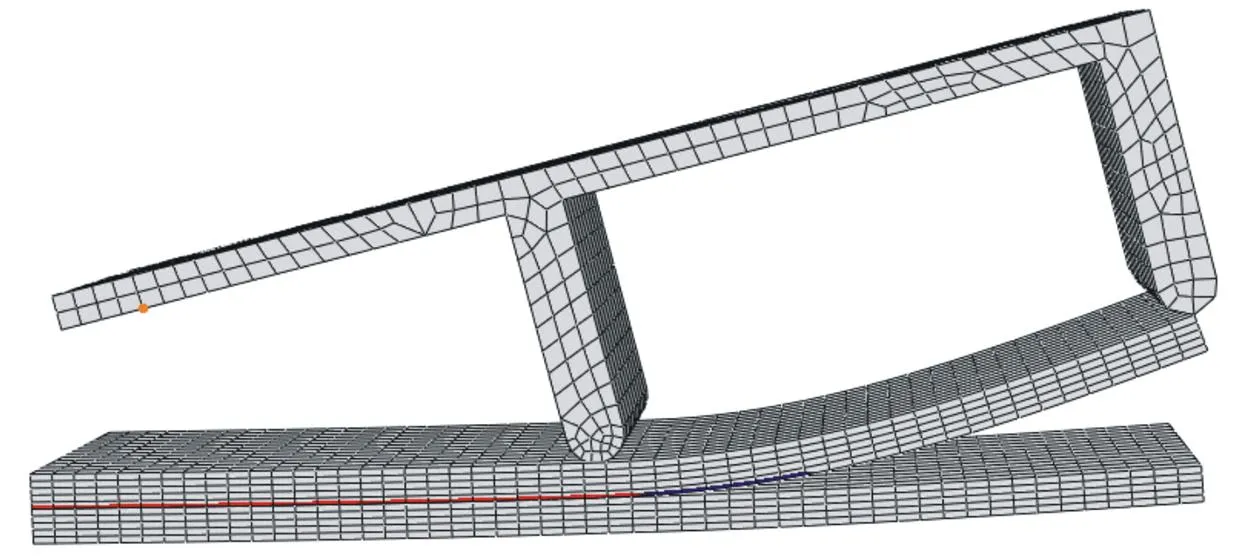
图6 界面脱黏失效裂纹扩展Fig.6 Interface viscous separation failure crack growth
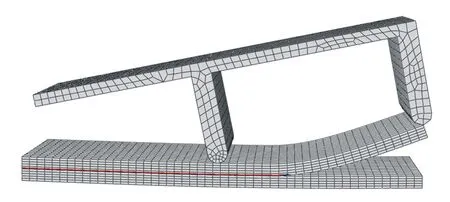
图7 层合板损伤失效-界面黏性剥离失效耦合失效裂纹扩展Fig.7 Laminate damage failure and interface viscous stripping failure Coupling failure crack propagation
考虑层合板损伤失效和界面脱黏失效两种失效模式耦合下试件损伤情况如图8所示,试件的位移-载荷曲线如图9所示。结果表明层合板主要发生基体拉伸、分层拉伸失效。综合图7~图9分析,两组数值仿真结果出现差异是因为在位移加载中,试件发生层合板损伤失效,导致层合板的力学性能发生退化,因此考虑两种失效模式耦合下产生的应力不能够让裂纹长度达到不考虑层合板损伤失效下裂纹长度一样的大小。

图8 复合材料层合板损伤Fig.8 Damage of composite laminates

图9 位移-载荷曲线图Fig.9 Displacement-load curve
两组数值仿真结果的位移载荷对比如图9所示。从图9中可以看出,随着位移载荷的施加,载荷突然下降,这是因为模型出现界面脱黏失效。根据图9,当位移载荷达到1.4 mm左右,考虑两种失效模式耦合下的数值仿真开始产生层合板损伤,之后其载荷变化随着位移载荷的加载与未考虑层合板损伤情况下数值仿真结果出现差异。当位移约为2.3 mm时,单失效模式下层合板与胶体相接触的界面开始发生分离,而当位移约为4.5 mm时,两种失效模式耦合下层合板界面开始发生黏性分离。
综上所述,层合板损伤与界面脱黏之间是一种互相耦合的关系。首先材料决定了层合板损伤、界面脱黏的发生初始载荷,因此在加载过程中,两种失效发生次序会因为材料的不同而发生变化。在位移载荷保持一致的情况下,若复合材料先发生层合板失效,这将导致层合板的力学性能会发生不可逆的退化,从而延迟了界面脱黏的出现;若复合材料先发生界面脱黏失效,则层合板损伤不会对其产生影响。同时,在载荷保持一致的情况下,由于界面脱黏失效的影响,导致层合板变形量变大,从而使得应力局部增高,当应力提高至一定值时,最终导致层合板损伤的产生。
3.2 多种失效模式耦合数值模拟
为探讨3种失效模式之间的内在联系,在原来模型的基础上考虑胶体厚度。由于胶体厚度为1 mm,故此处MMB模型长度和宽度没有发生变化,但模型整体厚度变为7.24 mm。胶体位于两块层合板中间处,其中初始裂纹长度为25.4 mm,宽度为15 mm。
层合板材料不变,依然为T300/1034-C,具体参数同表2,铺层顺序、单层板厚度以及数量不变。胶体材料选择AV138,具体参数如表3所示。
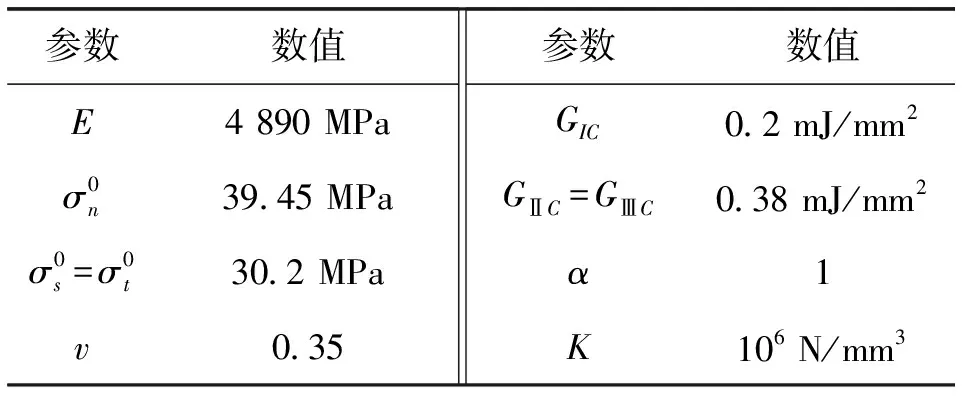
表3 AV138材料属性Tab.3 Material properties
图10为有胶体MMB有限元网格单元模型,在数值仿真过程中,本次CZM选择二次应力损伤准则,XFEM的损伤准则选择最大主应力损伤准则,二者断裂能判定均选择幂定律;层合板损伤失效判定公式仍为三维Hashin失效准则。
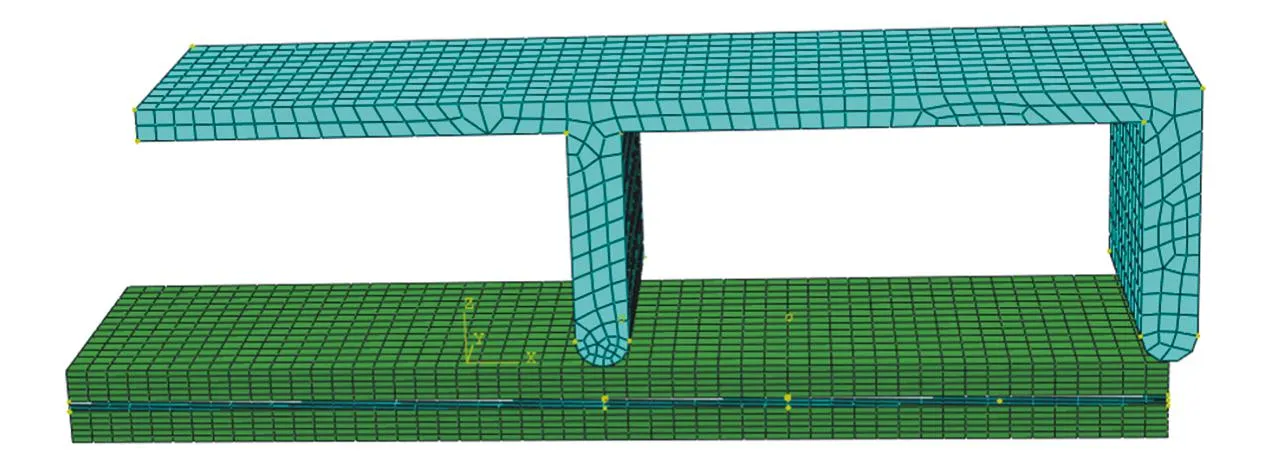
图10 有胶体厚度MMB有限元单元模型Fig.10 Finite element model of MMB with colloid thickness
由于要探讨3种失效模式之间的内在联系,本次数值仿真计算考虑两组情况,A组考虑界面脱黏和胶体裂纹扩展,B组考虑层合板损伤、界面脱黏和胶体裂纹扩展。
图11为两组数值仿真结果里胶体裂纹扩展路径,从图中可以看出两种情况下胶体裂纹扩展的路径存在差异。
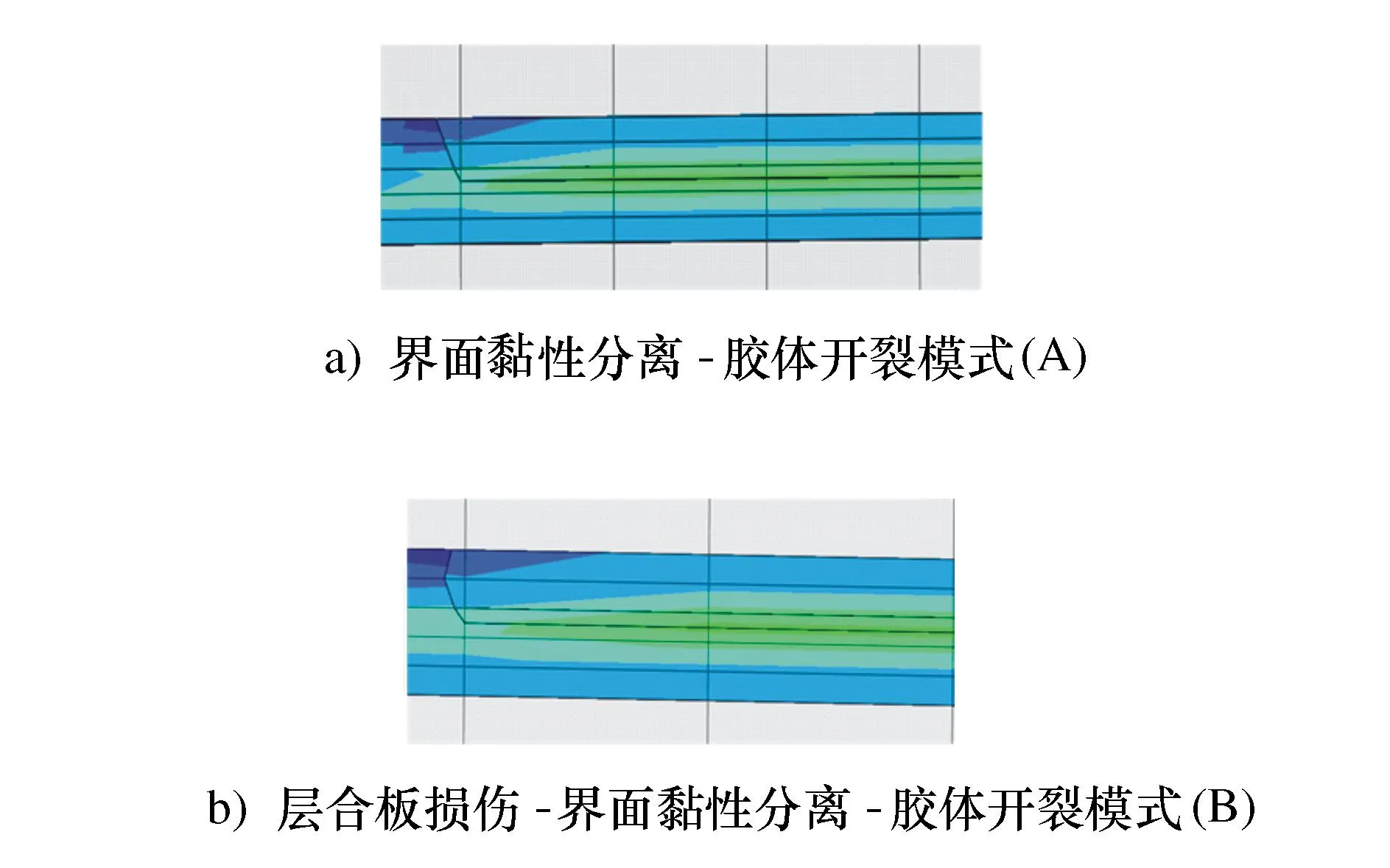
图11 胶体扩展路径Fig.11 Colloid expansion path
数值仿真结果表明层合板与胶体界面的分离是在胶体种裂纹扩展结束后才开始发生。A组胶体中裂纹一直朝左边扩展;B组胶体中裂纹扩展方向出现变化,导致左右两侧胶体没有分离,发生了与自锁相似的现象,之后位移载荷持续增大,只有当右侧胶体脱离层合板时,左侧层合板界面才会发生界面脱黏。
两组数值仿真位移载荷曲线如图12所示,两种失效模式耦合下,在发生界面脱黏失效前,载荷位移曲线呈线性增长,在开始发生界面脱黏失效后,载荷急剧下降,由于位移载荷的持续加载,层合板与胶体之间继续发生界面脱黏,从而使得载荷逐渐下降,最后当裂缝扩展至层合板中心位置附近才停止计算。
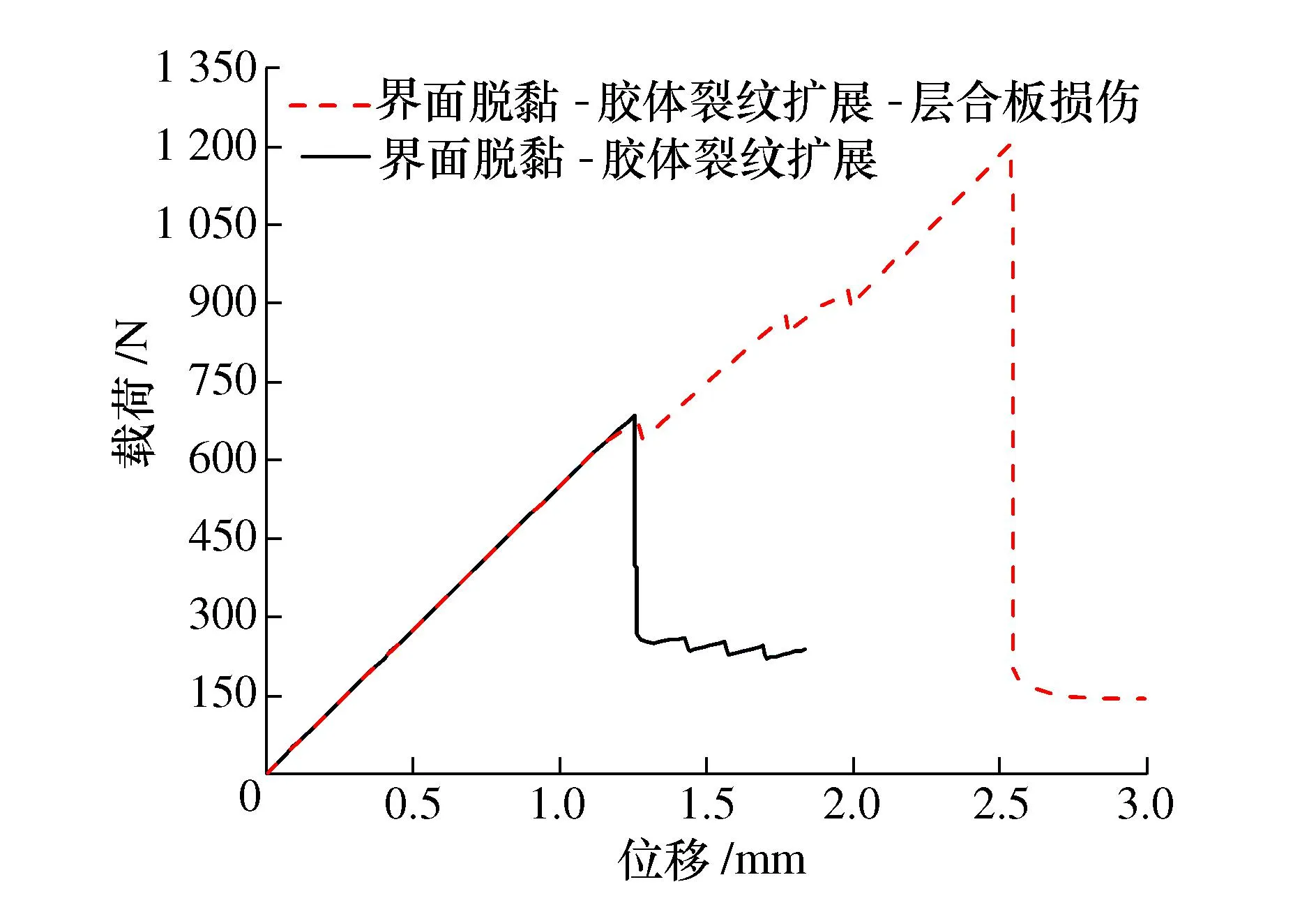
图12 位移载荷曲线图Fig.12 Displacement load curve
在3种失效模式影响下,在胶体中裂纹扩展的期间内,也产生了层合板损伤,从而降低了层合板的力学性能,最终导致胶体中裂纹扩展方向出现变化,且出现与自锁相似的现象。另外在位移载荷的加载过程中,受层合板损伤的影响,导致载荷位移曲线斜率发生变化。当右侧胶体与上层板完全分离后,裂缝开始沿着左边进行扩展,并于层合板中心位置附近停止计算。
两种失效模式耦合下层合板变形如图13所示,从数值仿真结果可以发现右侧胶体依然与上层合板黏结在一起。3种失效模式耦合下层合板变形如图14所示,图中右侧胶体与上层合板发生分离,并掉落在下层合板上。

图13 界面脱黏-胶体裂纹扩展Fig.13 Interface viscous separation and colloid crack growth

图14 界面脱黏-胶体裂纹扩展-层合板损伤Fig.14 Interface viscous separation, colloid crack growth and laminate damage
从两组数值仿真结果来看,胶体中裂纹的扩展路径存在差异是因为有无考虑层合板损伤失效。另外,MMB模型在3种失效模式共同作用下,出现了类似于自锁的现象,在某种程度来说,这种现象给复合材料带来正面影响,所以在研究复合材料的损伤问题是,要综合多种损伤失效进行分析。
4 结论
1) 根据混合模式弯曲梁分层实验[15]建立了MMB有限元分析模型,模拟了层合板在加载臂拉扯下的损伤过程,通过对数值仿真结果与实验结果的比较和分析,验证了MMB模型的正准确性。
2) 通过数值仿真结果的对比,层合板损伤与界面脱黏两种失效模式之间是互相耦合的关系:当黏性分离的临界载荷小于层合板强度,则两种失效模式互不影响,且只会发生界面脱黏失效;当层合板强度介于界面脱黏时的初始载荷和临界载荷两者之间,则两种损伤失效均会产生,随着位移载荷的增大,由于层合板损伤的作用,延缓了界面脱黏失效的出现。相对应的,随着力载荷的变大,由于界面脱黏失效的影响,加快了层合板损伤产生;当开始发生界面脱黏的初始载荷大于层合板强度,则只能产生层合板损伤。
3) 在3种失效模式共同作用下,胶体中裂纹的扩展路径会因为层合板损伤的出现变化,并导致类似于自锁现象的产生。因此在研究复合材料的损伤问题时,应该考虑多种失效模式耦合。

