考虑轮胎侧偏刚度在线更新的智能电动汽车状态估计
付越胜,李韶华,王桂洋
(1. 石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043; 2. 石家庄铁道大学 机械工程学院,石家庄 050043)
在道路行车数量增加和交通环境日益复杂的今天,行车安全受到了严峻挑战。配备高级驾驶辅助系统(Advanced driving assistance system,ADAS)的智能汽车以其能够减轻驾驶员的操作负荷并辅助驾驶员实现安全行车的特点成为研究热点。而准确实时地获取车辆行驶状态信息是实现智能汽车有效决策和控制的关键[1-2]。
目前,国内外学者对汽车状态参数估计方法的研究成果丰富,大都采用卡尔曼滤波及其改进形式,且结合各种方法提高算法的估计精度和鲁棒性。Eidfeld等采用无迹卡尔曼滤波(Unscented Kalman filter, UKF)算法对汽车的行驶状态和轮胎侧偏角进行了估计[3]。郝亮等将传统无迹卡尔曼滤波器和能够有效解决噪声时变特性的次优Sage-Husa噪声估计器相结合估计侧向车速和质心侧偏角[4]。戴一凡采用运动学方法建立卡尔曼滤波器,利用GPS提供的较为准确的车速和航向角信息对INS的偏差进行修正,并结合四轮轮速信息对纵向车速和质心侧偏角进行估计[5]。Katriniok等基于全球导航卫星系统(Global navigation satellite system,GNSS)设计了一种用于估计车辆纵向车速、侧向速度和横摆角速度的自适应EKF估计器[6]。Boada等提出了一种结合ANFIS和UKF的质心侧偏角估计方法以减小UKF估计器的噪声干扰[7]。王震坡等将模糊控制引入到无迹卡尔曼滤波算法中,对车辆横摆角速度、质心侧偏角和纵向车速进行估计[8]。方贤生等采用相同的方法对系统测量噪声协方差进行自适应调整,两者不同之处在于方贤生在模糊控制器的输入端建立了输入因子变化率的模糊集[9]。冯亦奇等提出了一种利用遗忘因子对噪声协方差矩阵进行自适应调整的无迹卡尔曼滤波方法,实现车辆状态参数在线估计[10]。张志达等提出一种基于故障检测机制对观测噪声协方差和过程噪声协方差进行自适应调整的鲁棒自适应UKF算法, 估计车辆的纵向车速、侧向车速和质心侧偏角[11]。Rodrigo等基于汽车内置传感器和惯性测量单元提出了一种多传感器融合方案,对车辆的三维速度和姿态角(俯仰和侧倾)进行估计,通过实验证明了该方法在常规城市驾驶和防撞操作中的有效性[12]。
以上的研究为提高车辆状态参数的估计效果,都倾向于实现算法的自适应或降低噪声干扰而忽略了模型参数的时变本质。为此,陈瑶提出一种双重扩展自适应卡尔曼滤波算法对车辆行驶状态和车身参数(整车质量、车体转动惯量和质心位置)进行联合估计,以提高状态参数估计精度[13]。陆辉等利用两个平行扩展卡尔曼滤波器分别估计轮胎侧向力与侧偏刚度,降低了对轮胎模型精度的依赖,有效保证了不同轮胎特性下的侧向力估计精度[14]。文献[13-14]都采用了双重扩展卡尔曼滤波算法进行参数和状态的联合估计,但都未考虑观测噪声的时变特性对算法的负面影响,因此算法的适用性受到限制。罗文发等分别建立了纵向车速、路面附着系数和轮胎侧偏刚度观测器,并将其观测值作为质心侧偏角估计器的输入[15]。文献[15]共建立了4个观测器并通过外部接口进行连接,然而实际运用中恐会出现参数反馈不及时和系统计算负担过大等问题,从而导致算法实时性变差甚至失效。
基于以上分析,本文提出了轮胎侧偏刚度在线更新的汽车状态估计算法,将估计轮胎侧偏刚度的FFRLS算法嵌入到估计车辆状态的FAEKF算法中,保证算法的实时性和鲁棒性,并且轮胎侧偏刚度估计的输入量(纵向车速和横摆角速度)为不含噪声的状态预测值,降低了观测噪声对轮胎侧偏刚度估计的影响。因此可实现车辆行驶状态和轮胎侧偏刚度高精度的联合估计。
1 电动汽车动力学模型
1.1 三自由度整车模型
线性二自由度整车模型假设纵向车速恒定不变,只考虑车辆的侧向和横摆运动,而三自由度整车模型在此基础上考虑车辆纵向车速的变化,变化的纵向车速对汽车的横摆和侧向运动有显著的影响,且构成状态变量之间的非线性关系[16]。本文建立三自由度整车模型以估计车辆的纵向车速、横摆角速度和质心侧偏角。建模中忽略了车辆俯仰和侧倾方向的运动;忽略悬架系统转向系统的影响和空气阻力的影响[17]。三自由度整车动力学模型如图1所示。
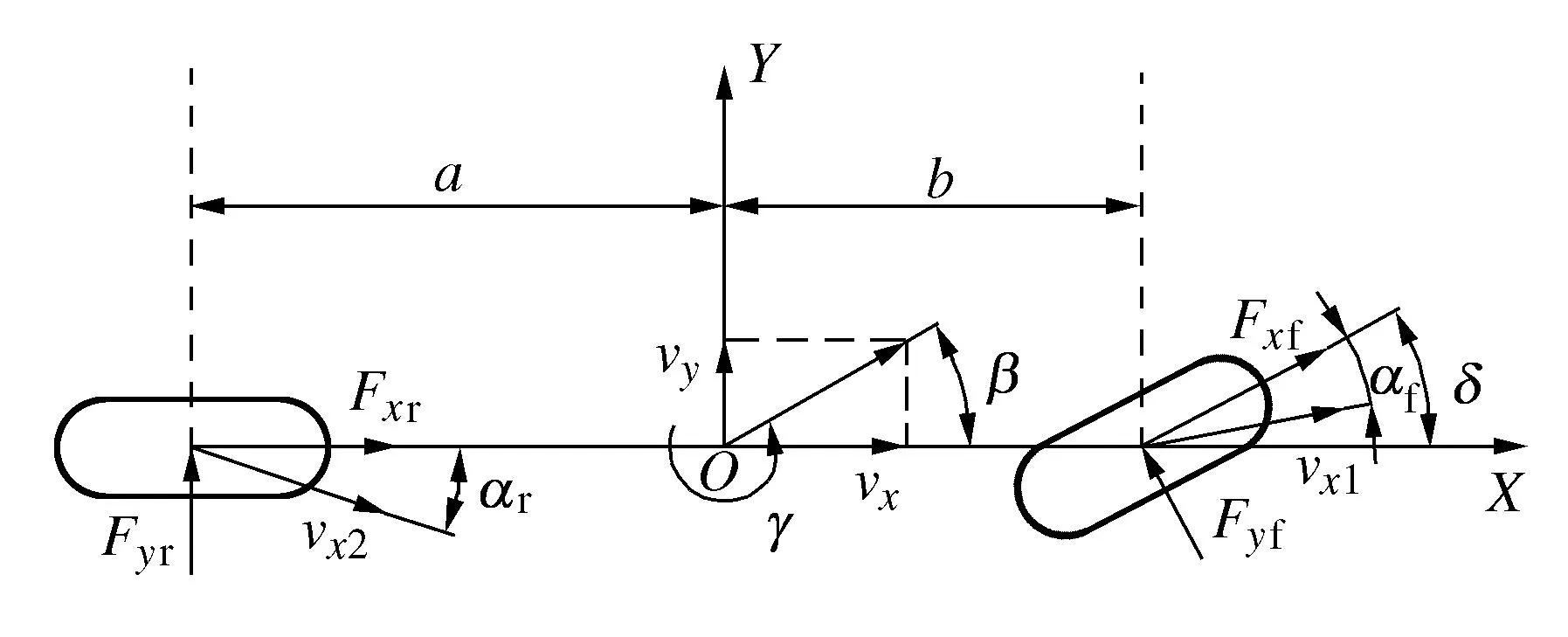
图1 三自由度整车动力学模型Fig.1 3-DOF vehicle dynamics model
纵向运动方程为
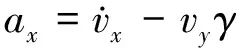
(1)
Fxfcosδ-Fyfsinδ+Fxr=max
(2)
侧向运动方程为

(3)
Fxfsinδ+Fyfcosδ+Fyr=may
(4)
横摆运动方程为
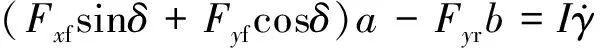
(5)
式中:vx、xy、β、γ分别为车辆的纵向车速、侧向车速、质心侧偏角和横摆角速度;δ、m分别为前轮转角和整车质量;a、b分别为车辆前后轴到质心的纵向距离;Fxi、Fyi分别为车辆前后轴的纵向力和侧向力。
1.2 轮胎模型
车辆在正常行驶时,一般认为轮胎侧偏力与侧偏角成线性关系。在极限工况下,轮胎处于非线性状态,线性轮胎模型无法满足建模精度要求,但车辆在行驶过程中任意时刻的轮胎侧偏力和侧偏角的关系可用式(6)表示,只是此时的轮胎侧偏刚度不再当作一个常量而是具有时变特性的动态参数。
Fyi=Ciαi
(6)
式中:Ci为轮胎侧偏刚度;αi为轮胎侧偏角。

本文采用式(6)所示的轮胎模型,并在车辆状态估计中采用带遗忘因子递推最小二乘方法实时更新轮胎侧偏刚度,以此描述轮胎的非线性刚度。
1.3 车轮纵向力
本文中智能电动汽车为轮毂电机总成附带单级行星齿轮减速器的驱动方式,其 4个车轮直接由电机独立驱动,电机的转矩和转速容易测量,因此可利用车轮动力学模型计算轮胎纵向力[18]。车轮旋转动力学模型和车轮转矩的表达式为:

(7)
Tdij=ξTqijη
(8)
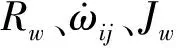
由此,各车轮纵向力可表示为

(9)
车辆模型中的前后轴纵向力的计算公式为

(10)
2 模糊自适应扩展卡尔曼滤波状态估计
2.1 车辆状态估计
车辆非线性系统可表示为以下状态方程和观测方程的形式:
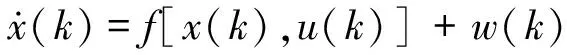
(11)
y(t)=h[x(t)]+z(t)
(12)
式中:x(t)为状态变量;u(t)为系统输入量;y(t)为观测向量;w(t)为满足均值为零,协方差为常值矩阵Q的系统过程噪声;z(t)为满足均值为零,协方差具有时变特性的观测噪声,且w(t)与z(t)不相关。
结合三自由度整车动力学模型,将车辆系统表示为状态方程和观测方程。
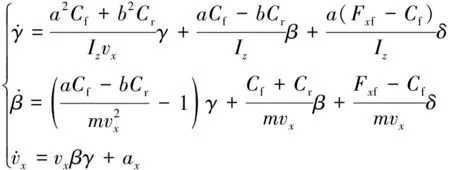
(13)
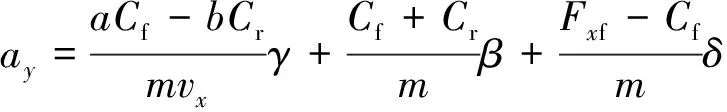
(14)
由式(13)与式(14)得:状态向量为x=[γ,β,vx]T,系统输入量为u=[Fxf,Fxr,δ,ax]T,观测量为y=[ay]。
求解式(13)、式(14) 的雅克比矩阵,并对其进行线性化处理。
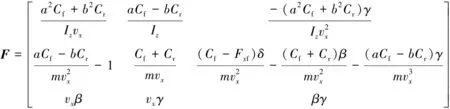
(15)
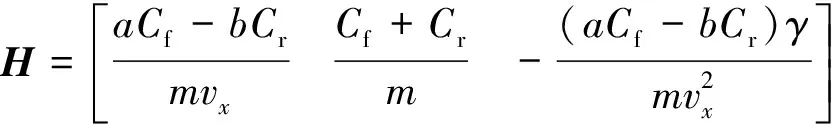
(16)
采用欧拉算法对系统进行离散化处理,得到状态转移矩阵Φ=I+FT,T为采样时间。
将相关矩阵和向量代入EKF算法流程进行迭代运算[13],具体如下:
1) 时间更新方程为:
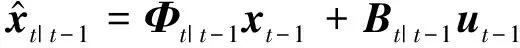
(17)
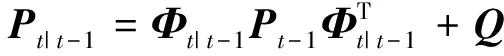
(18)
2) 测量更新方程为:
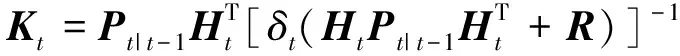
(19)
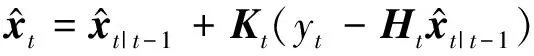
(20)
Pt=(I-KtHt)Pt|t-1
(21)
式中:Pt为误差协方差矩阵;Q、R分别为系统过程噪声和测量噪声协方差矩阵;Kt为卡尔曼增益矩阵;δt为时变调整因子。
将模糊控制器与EKF算法相结合,形成模糊自适应扩展卡尔曼滤波算法(FAEKF),该算法通过实时调整包含观测噪声协方差R的Clt来调整卡尔曼增益,既可实现算法的自适应效果,又有利于减小估计误差。控制器以EKF算法中观测量的实际残差的协方差与理论残差的协方差之比为输入,以协方差Clt的调整因子为输出。残差定义为观测量的实际值与预测值之间的误差[18],由式(19)与式(20)得:
理论残差的协方差为
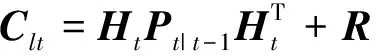
(22)
实际残差为
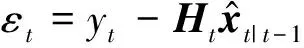
(23)
定义实际残差的协方差为
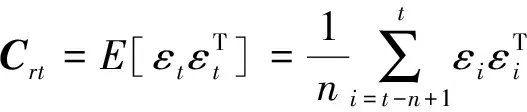
(24)
式中n为新近的残差数量,其取值过大会导致Clt较大的计算误差且算法收敛变慢,取值过小则会引起Clt计算值波动较大,不利于算法运行。
1) 定义控制器输入输出变量
由观测向量y=[ay]1×1可知残差的协方差为单元素矩阵。定义输入变量及其论域为
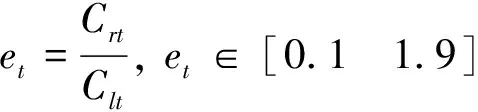
(25)
在控制器中设置合理的模糊规则,根据输入et得到调整因子δt。由式(24)所得实际残差的协方差会由于n的覆盖范围带来计算误差,为避免过度修正再次引入误差[19],调整因子取值范围略小于[0.1,1.9],故将其论域设置为δt∈[0.2,1.8]。
2) 设计模糊逻辑规则
将控制器的输入与输出变量的论域均划分为3个模糊子集,其中L<1,E≈1,G>1。建立模糊规则:
IfetisL, thenδtisL
IfetisE, thenδtisE
IfetisG, thenδtisG
隶属度函数选择三角型隶属度函数,解模糊化方法选择常用的重心法,利用MATLAB模糊工具箱生成fis文件,在Simulink中直接调用此文件完成控制器的建立[20]。
2.2 轮胎侧偏刚度在线估计
由于前文的状态估计包括质心侧偏角,考虑其估计难度较大,在侧偏刚度的估计中避开以质心侧偏角为输入量。采用侧向-横摆综合法[21],考虑前轮纵向力的影响,结合式(4)和式(5)将车辆的运动方程表示为:
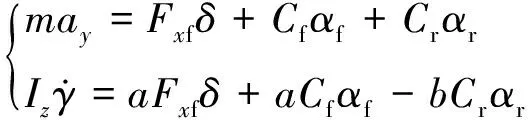
(26)
将式(26)中的质心侧偏角β消去,得到其矩阵表达式为
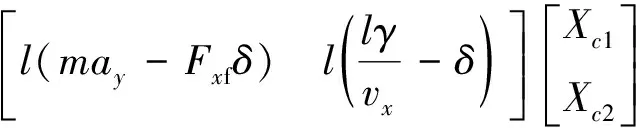
(27)
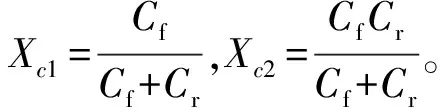
因此,轮胎的侧偏刚度可表示为:
(28)
带有遗忘因子递推最小二乘法(FFRLS)在已知模型输入输出数据的基础上,可以便捷地求得未知的系统参数,并使得估计误差的平方和最小[17]。故采用FFRLS算法进行轮胎侧偏刚度在线估计。
为避免对横摆角速度求导带来额外噪声,对式(27)进行时间上的离散化处理,得到估计器的输入、输出与待估计参数表达式分别为:
系统输入表达式为
φT(t)=

(29)
系统输出表达式为
Y(t)=bmay(t)T+Iz(γ(t)-γ(t-1))-lFxf(t)δ(t)T
(30)
待估计参数表达式为

(31)
FFRLS算法表达式为:
(32)
式中:χ(t)为递推增益矩阵;P(t)为协方差矩阵;λ为遗忘因子,其取值范围为(0,1],取值越大则辨识精度越高,但是收敛速度变慢;反之则辨识精度降低,但收敛速度会变快[22]。因此需要综合考虑λ的取值。
将式(29)~式(31)代入FFRLS算法表达式(32)中进行迭代运算,可得到中间变量θ(t),再通过式(28)换算得到轮胎侧偏刚度。
2.3 状态和参数联合估计
前文分别建立了基于FAEKF算法的车辆状态估计模型和基于FFRLS算法的轮胎侧偏刚度估计模型。为提高状态参数估计精度,本文将两种算法以嵌入式的方式进行结合组成FAEKF+FFRLS算法,在完成车辆状态估计的同时实现轮胎侧偏刚度在线更新,算法流程如图2所示。
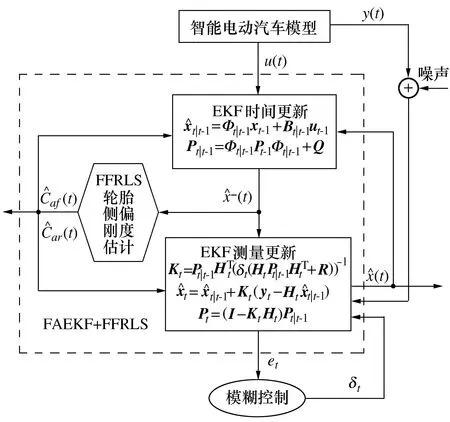
图2 联合估计算法流程Fig.2 Procedures of joint estimation algorithm
3 仿真验证及误差分析
在Trucksim中选择与车型CC1031PA41A的技术参数相近的皮卡车作为整车模型基础,建立车体模型、空气动力学模型、悬架系统模型、轮胎模型等,在Simulink中建立电机模型和驾驶员速度控制模型[10]。将Trucksim中燃油车的传动系统和发动机模块删去,车轮的驱动方式设置为外部输入,并设置正确的输入输出接口与Simulink中的电机模型和驾驶员速度控制模型进行连接,完成车辆建模,车辆的驱动原理如图3所示。
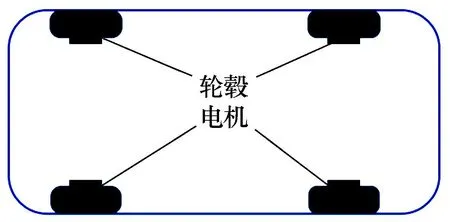
图3 电动汽车驱动原理图Fig.3 The driving principle diagram of electric vehicles
由图3可知,所建立的电动汽车模型的驱动方式为四轮独立驱动,4个车轮由参数完全相同的轮毂电机构成。轮毂电机接收电流信号后产生转矩,通过减速器后将增大的转矩输出传递给车轮产生车辆前进的动力。整车参数如表1所示,减速驱动轮毂电机内部结构如图4所示。
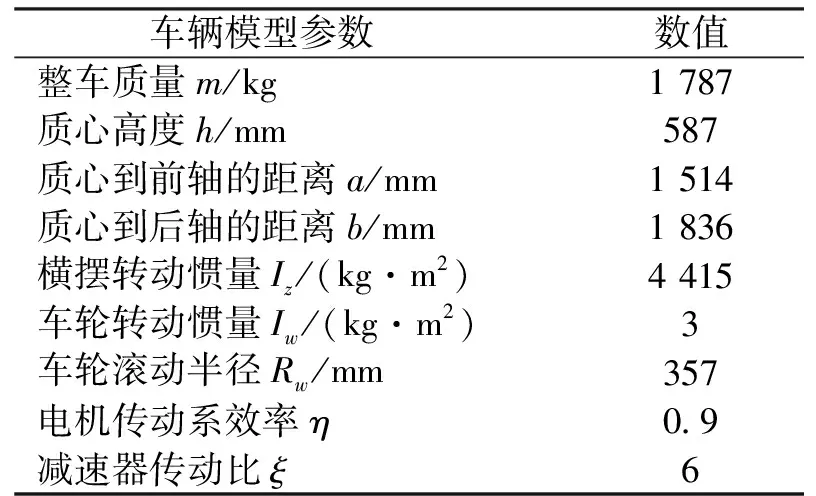
表1 整车参数Tab.1 Vehicle parameters
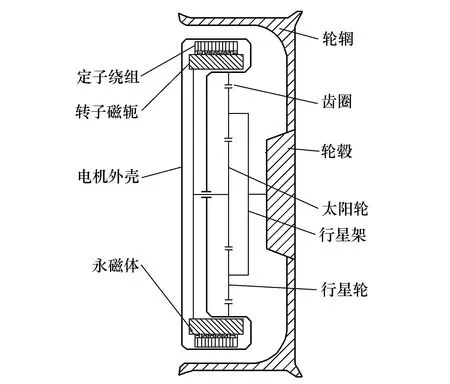
图4 减速驱动轮毂电机结构图Fig.4 Structurs of deceleration drive hub motor
电机采用内转子形式更易实现高速运转,其最大功率为20 kW,最高转速为9 000 r/min,并配备固定传动比为6∶1的行星齿轮减速器,从图4中可以看出电机输出转矩通过减速器完成减速增矩后由行星架传递给车轮。
为验证所提出估计算法的有效性和鲁棒性,选择不同车速、不同路面附着系数的双移线工况进行仿真,并将所提出的联合估计算法结果、标准EKF算法结果和Trucksim输出的参考值进行对比分析。
工况1:初始车速为30 km/h,附着系数0.3。
工况2:初始车速为80 km/h,附着系数0.8。
工况3:初始车速为80 km/h,附着系数0.3。
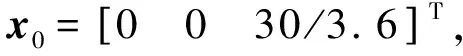
FFRLS算法:误差协方差矩阵P0=100*I3×3;遗忘因子λ=0.99; 轮胎侧偏刚度初始值C0=
估计器的测量输入为含有时变噪声的侧向加速度,如图5所示。
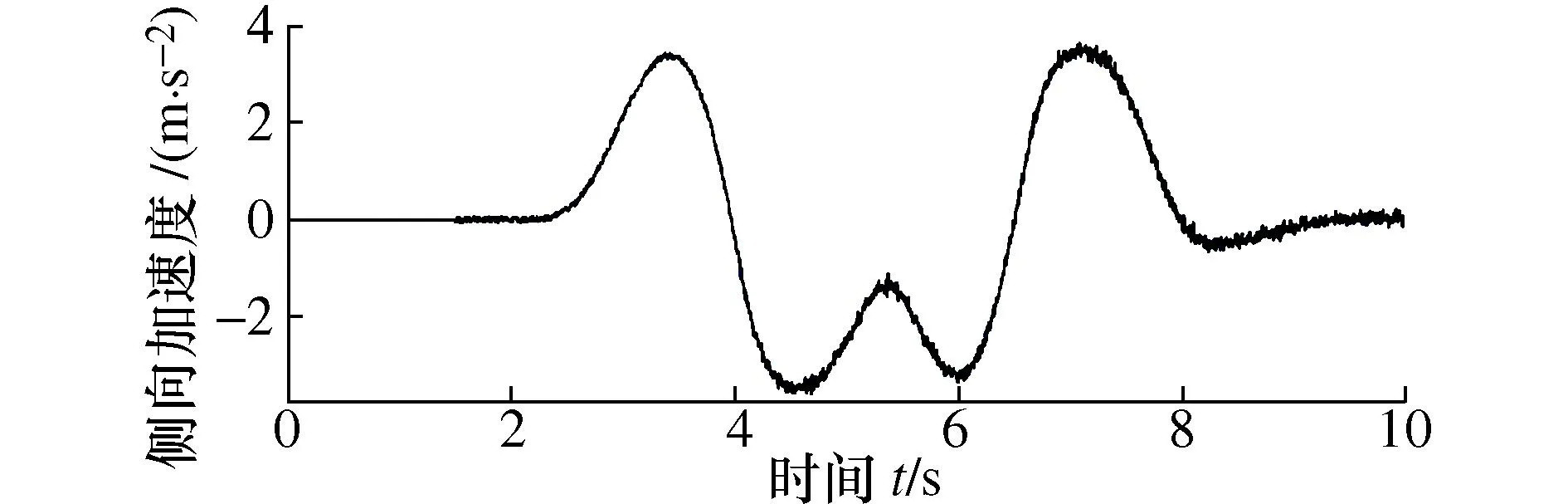
图5 含时变噪声的侧向加速度(工况2)Fig.5 Lateral acceleration with time-varying noise (operating condition 2)
由FFRLS+FAEKF估计器在估计车辆状态的同时输出前后轮的轮胎侧偏刚度的估计值。为分析轮胎侧偏刚度的估计效果,将轮胎侧偏刚度估计值与参考值进行对比分析。在此3种工况下进行整车仿真,通过对输出的轮胎侧偏力和侧偏角进行线性拟合得到轮胎侧偏刚度参考值,如表2所示。
由表2可知:3种工况得到的轮胎侧偏刚度参考值各不相同,其中工况1和工况2非常接近,而工况3则有明显差异,可见车速和路面附着系数均对轮胎侧偏刚度有影响。本文中前轮侧偏刚度代表左前轮与右前轮轮胎侧偏刚度之和,后轮侧偏刚度同理。
由估计器得到的轮胎侧偏刚度估计值与参考值对比如图6所示。

图6 轮胎侧偏刚度估计值与参考值Fig.6 Estimated and reference values of tire cornering stiffness
从图6可知:在轮胎侧偏刚度估计进入稳态后,前轮侧偏刚度和后轮侧偏刚度估计值都能很好的跟随参考值,并在其上下浮动,反映出轮胎侧偏刚度在车辆行驶过程中的时变特性;由图6a)、图6b)可知:前轮、后轮侧偏刚度估计值与参考值的最大差值均出现在第7.5 s附近,其估计误差分别为8.2%和9.5%,之后估计值迅速靠近参考值,并伴有小幅波动,整个过程轮胎处于弱非线性状态;分析图6c)、图6d)可得:前轮、后轮侧偏刚度最大估计误差出现在第2.3 s附近,分别为5.6%和9.4%;由图6e)、图6f)可知:前轮、后轮侧偏刚度最大估计误差均出现在第2.3 s附近,分别为7.4%和9.6%。工况2和工况3中,轮胎侧偏刚度估计值有较大波动,轮胎均处于强非线性状态。
车辆的纵向车速、横摆角速度和质心侧偏角估计结果如图7~图9所示。
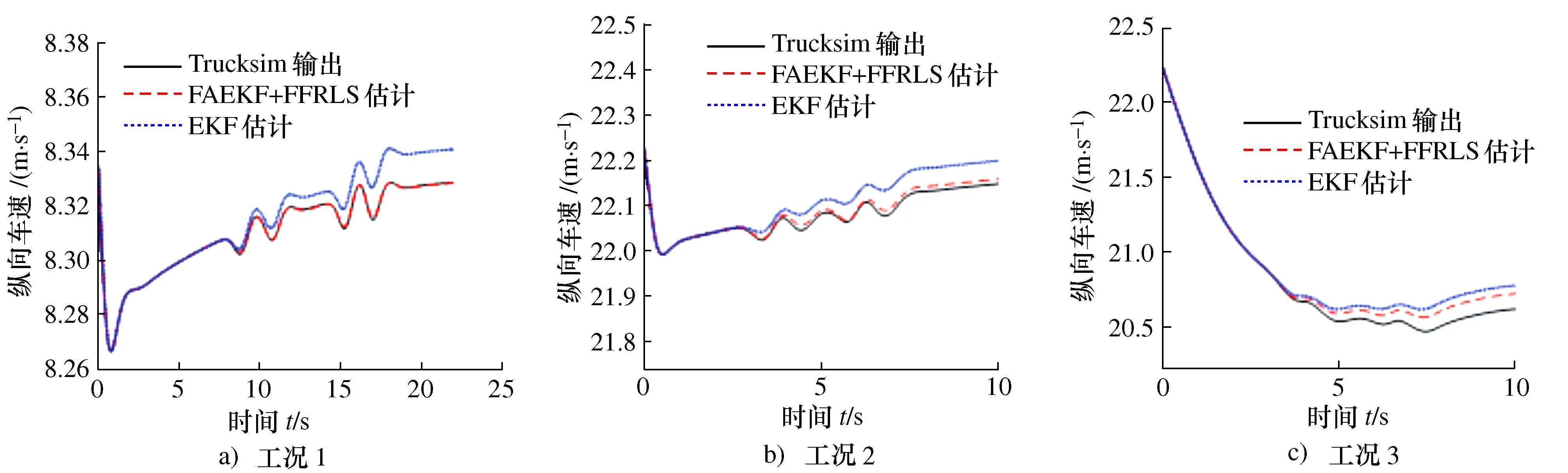
图7 纵向车速估计结果对比Fig.7 Comparison of estimated results of longitudinal vehicle speed
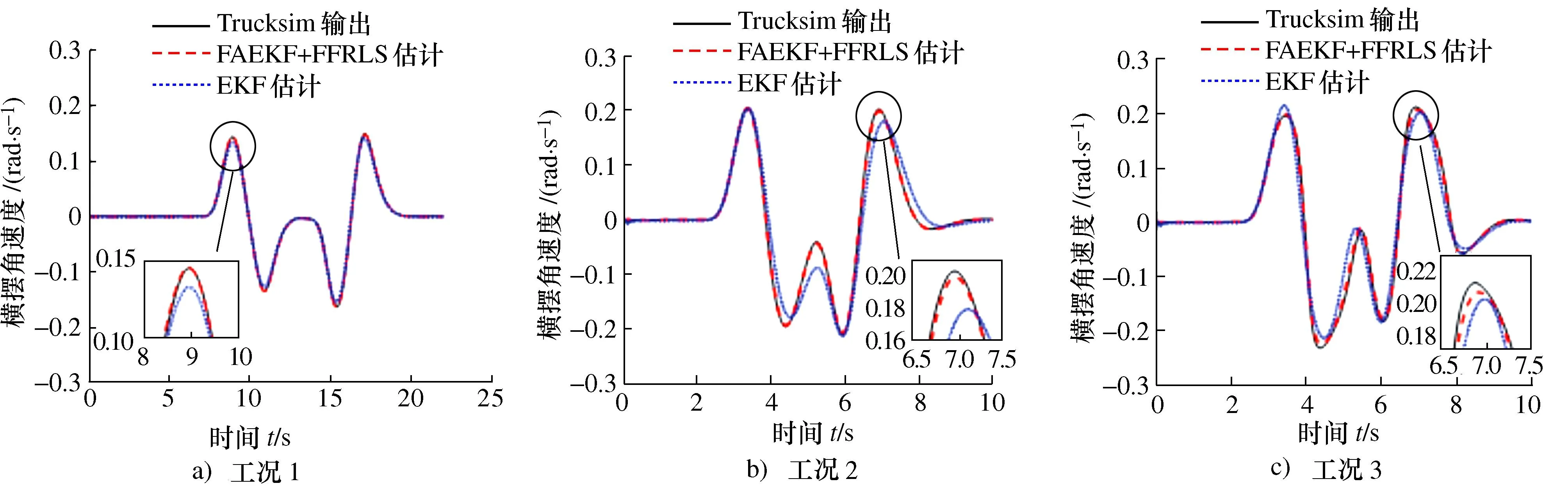
图8 横摆角速度估计结果对比Fig.8 Comparison of estimated results of yaw rate

图9 质心侧偏角估计结果对比Fig.9 Comparison of estimated results of sideslip angle
从图7~图9可以看出:FAEKF+FFRLS算法对这3种状态的估计精度都较高且优于标准EKF算法;其中工况1车辆处于弱非线性状态,两种算法估计效果差距不明显,而工况2和工况3中FAEKF+FFRLS算法所得估计值对参考值的跟随能力明显优于标准EKF算法,表现出了更高的估计精度和鲁棒性;由图7可知:两种算法对纵向车速的估计精度都很高,整个过程中估计值的最大相对误差均小于1%;图8与图9中的局部放大图代表FAEKF+FFRLS算法估计结果的最大绝对误差,两种算法在此处估计值的具体相对误差如表3所示。
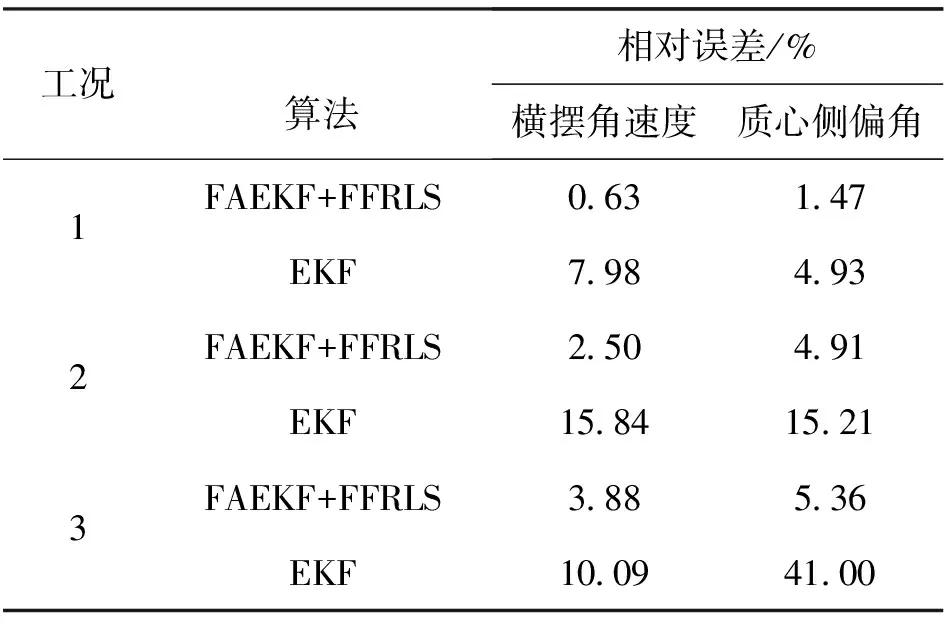
表3 估计值的相对误差
由表3可知:同种工况下相比于标准EKF算法,FAEKF+FFRLS算法估计结果的相对误差都有较大的改善,其中工况3质心侧偏角估计值的相对误差降低了35.64%; 从工况1到工况3极限性不断提高,两种算法的估计结果的相对误差都有所增大,但FAEKF+FFRLS算法估计值的最大相对误差为5.36%,仍具有较高精度。对比3种工况可知其他条件不变时,车速越高算法估计精度越低,路面附着系数越低算法估计精度越低。
因此,所提出的FAEKF+FFRLS算法比标准EKF算法具有更高的精度、更好的稳定性和鲁棒性。
4 结论
综合算法参数自适应和轮胎侧偏刚度在线更新,提出了一种汽车状态估计FAEKF+FFRLS算法。利用Trucksim和MATLAB/Simulink联合仿真,通过与标准EKF算法对比,验证了所提算法的效果。研究表明:
1) 与传统汽车模型不同,在建立估计模型时利用分布式驱动电动汽车转矩和转速容易测量的特点建立轮胎纵向力计算模型。并将其引入到车辆状态和轮胎侧偏刚度估计模型中,提高了建模精度,为后续的车辆状态估计奠定模型基础。
2) 提出的FAEKF+FFRLS估计算法,将轮胎侧偏刚度当作随时间变化的动态参数来处理,提高了车辆状态的估计精度。其估计结果优于标准EKF算法,具有较好的鲁棒性和估计精度。
3) 采用模糊控制器对算法中的卡尔曼增益矩阵进行实时调整,使算法更好地适应带有时变观测噪声的输入信息,提高了算法的鲁棒性。

