频响函数残差法在有限元模型修正中的应用

屈晶晶，张立民，邱飞力，周　辉

（西南交通大学 牵引动力国家重点实验室，成都 610031）



频响函数残差法在有限元模型修正中的应用

屈晶晶，张立民，邱飞力，周辉

（西南交通大学 牵引动力国家重点实验室，成都 610031）

准确的有限元模型能够真实有效地反映实际结构的动态信息，为缩小结构建模中的误差极有必要对结构有限元模型进行修正。目前，基于模态频率、振型和频响函数的模型修正方法应用最广。其中基于频响函数的修正方法避免了模态参数识别过程的误差，且不受测试自由度数限制，与模态频率和振型的模型修正方法相比更具有优势。基于频响函数的修正方法按目标可分为频响函数相关性法和频响函数残差法。频响相关性法立足于形状和幅值相关性与参数灵敏度的关系，与频响函数残差法相比，丧失了频响函数与设计参数的直接关联，导致在部分结构模型修正中出现振荡不收敛现象。为此，基于实际测试结构对比研究两种方法在有限元模型修正中的应用，并分析频率点数和频带范围对基于频响函数残差法的模型修正的影响。结果表明频响函数残差法能够稳定收敛且具有高效性；同时，合理的频率点数和较宽频带范围有利于提高频响函数残差法的修正效率。

振动与波；模型修正；频响灵敏度；频率点数；频带范围

准确的有限元模型能够真实有效地反映实际结构的动态特性，从而对结构的设计和优化提供可靠指导。对实际结构而言，难以建立与其动态性能完全一致的有限元模型。即在有限元建模过程中，不可避免地存在误差，进而影响模型的计算精度。为缩小有限元模型的误差，有必要对有限元模型进行修正［1］。

为避免模型修正的盲目性，采用灵敏度分析确定特征量对修正参数的敏感程度［2］，进而确立模型参数的修改方向以符合实际结构特性。结合设计参数的灵敏度，以结构的动态特征为目标的模型修正方法成为了当前研究的热点。其中，基于结构模态频率、振型和频响函数的修正方法应用最为广泛［1-5］。基于模态频率和振型的修正方法，需要足够的测试自由度同时依赖于模态识别的精度，这将增加测试工作量且在修正过程中引入了模态分析误差，增加了修正的难度［5］。基于频响函数的模型修正方法，所必需的测试自由度较少，降低了测试工作量且不需要模态参数识别，降低了测试数据的误差［6］。

频响函数修正方法按修正目标的不同可分为频响函数相关性法［7-8］和频响函数残差法。频响相关性法失去了设计参数与结构特征量的直接关系，在结构修正中可能不收敛。频响相关性法的缺陷，可采用频响函数残差法进行弥补。同时，基于频响函数相关系数的期望和标准差建立的模型精度判定准则，可评价实测与仿真数据的一致性程度［9］。

1　基于频响函数模型修正方法

1.1频响函数相关性法

离散系统的频响函数计算表达式为［10］

其中［K］、［M］和［C］分别为结构的刚度矩阵、质量矩阵和阻尼矩阵。

频响函数相关系数反映频响函数测试值与仿真值的一致性程度，其具体分为形状相关性和幅值相关性。频响函数形状相关性计算表达式为

为克服形状相关性函数的不足，引入幅值相关系数，其计算表达式如式（3）所示。

基于频响函数相关性系数的模型修正方法，其目标函数可以用式（4）表示。

即

其中｛ε｝为相关系数残差，［S1］为频响函数相关系数的灵敏度矩阵，｛Δ p｝ 为有限元修正参数的的迭代值。

利用扩展加权的最小二乘法，目标函数转换为

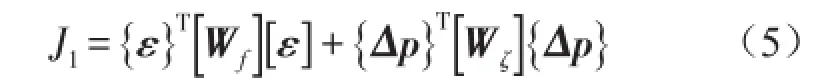
其中

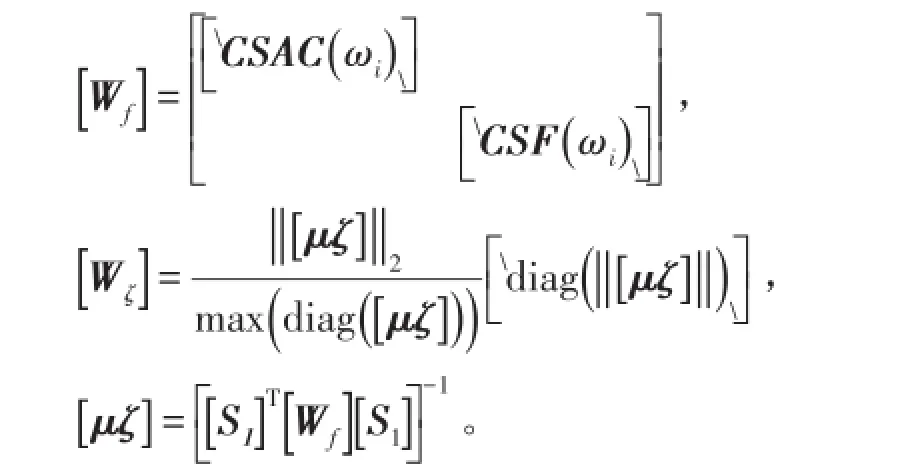
采用Link法对其求解［11］，单次迭代设计参数改变量如式（11）所示。

1.2频响函数残差法

频响函数灵敏度可表示为频响函数对设计参数的偏导数，如式（7）所示。

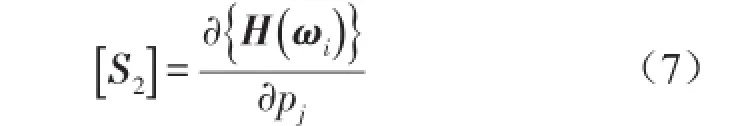
结合泰勒级数展开公式并忽略高阶项，则有

将式（7）代入式（8）中，并利用差分原理化简可得

［S2］为结构频响函数对设计参数的灵敏度矩阵。结合频响函数灵敏度计算式（9），有限元模型修正方程可表示为

｛pu｝为结构参数真实值。化简可得

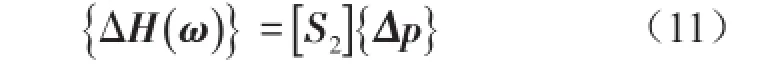
｛ΔH（ω）｝为频响函数残差；｛Δp｝为参数的改变量。

将式（11）改写成为优化求解的目标函数

式（12）通常情况下为超定方程组，采用广义逆方法进行求解，如式（13）所示。

1.3精度判定准则

频响函数相关系数的期望和标准差分别表示为式（14）-式（17）所示。

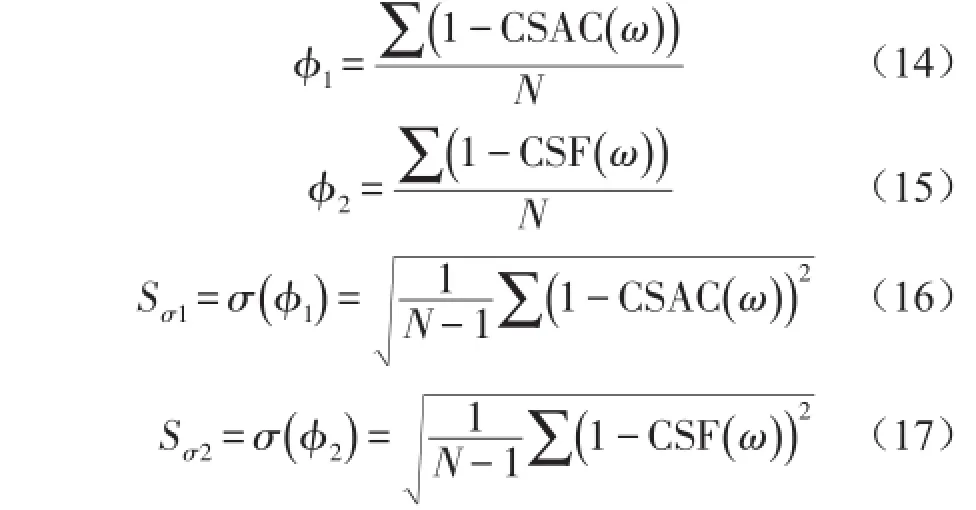
结合式（14）—式（17），建立精度判定准则如式（18）所示。

若式（18）成立，表明模型满足精度修正完成；否则，仿真模型不满足精度，需要继续迭代修正。

2　算例验证

2.1频响测试

某支架结构由槽钢、方钢和角钢3种型材组成。采用冲击激励法，估计结构在0～120 Hz范围内频响函数。现场试验照片如图1所示。

图1　支架频响测试

2.2有限元谐响应分析

有限元模型主要参数如表1所示。

实际支架为弹簧弹性支撑，在有限元模型中采用弹簧单元（COMBIN 14）进行模拟，支撑刚度由实际支架结构刚体模态和质量计算，如式（19）—式（20）所示。

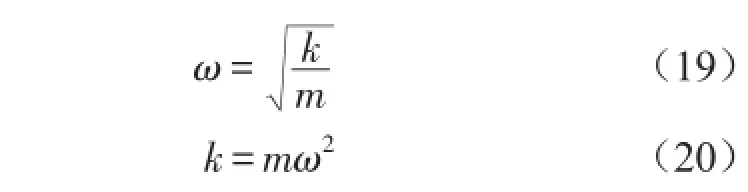
其中ω为实际支架结构刚体模态频率，k为支撑刚度，m为支架质量。

有限元模型如图2所示。

图2　支架有限元模型

表1　支架模型初始参数表

对有限元模型进行谐响应分析，得到测点的频响函数图，与测试结果对比如图3所示。

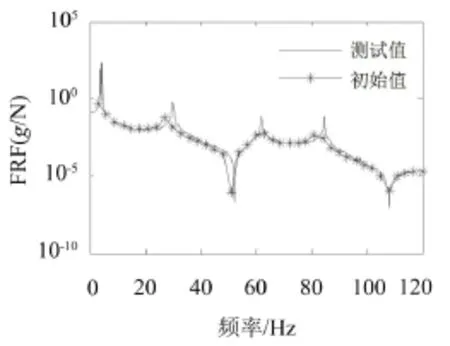
图3　初始模型频响函数与测试频响函数对比

根据式（19）—式（22），初始模型频响函数相关系数的期望和标准差为：Sσ1=1.49×10-16，Sσ2=0.09，ϕ1=2.16×10-17，ϕ2=0.02，Sσ2和 ϕ2不满足式（18），说明仿真模型不满足精度，需要修正。

2.3修正算法对比

采用频响函数相关性法（以下简称“方法1”）和频响函数残差法（以下简称“方法2”）对支架有限元模型进行修正（说明：为借助文献［12］的最终修正参数作为本文支架模型修正的参考值，在后续的仿真计算中如未特别说明，频带范围均取0～100 Hz）。

在40次迭代后，两种方法修正后的模型频响函数相关系数期望ϕ最大值为0.001 8，均满足精度判定准则，鉴于篇幅原因此处未给出。频响函数相关系数标准差Sσ随迭代次数变化见图4。

由图4可知，迭代40次后，方法1标准差Sσ1随迭代次数增加处于阀值界定线之下，而Sσ2呈振荡状态；方法2标准差Sσ1和Sσ2随迭代次数增加均处于阀值界定线之下，满足判定准则。

*方法1Sσ1　oo方法1Sσ2　··方法2Sσ1　++方法2Sσ2——标准差0.03阀值界定线图4迭代变化图

这表明方法1对本支架结构的模型修正效率明显低于方法2，其原因在于方法1失去了设计参数与频响函数的直接关联信息。

测点频响函数仿真与测试值对比如图5所示。

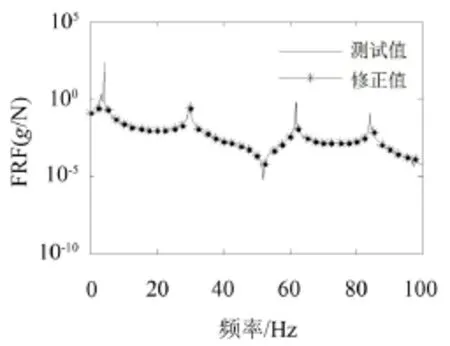
图5　修正模型频响函数与测试频响函数对比

由图5可知，基于方法2修正后的模型频响函数与测试频响函数高度吻合，表明了经方法2修正后的模型能够反映结构的动态特性。

方法2修正后的模型参数与支架结构参数参考值［12］对比如表2所示。

由表2可知，修正后的模型参数最大误差为0.36%，与模态频率修正方法获取的参数值高度吻合，验证了频响函数残差法的有效性与实用性。

3　频响函数残差法影响因素

3.1频响函数点数

频响函数点数会影响模型修正质量，此处研究频率点数分别在200点、400点、600点、800点和1 000点工况下，支架模型修正效果的变化规律。

标准差Sσ2随迭代次数变化如图6所示（Sσ1数量级均为10-16，满足判定准则，故不再画出）。

由图6可知，截止40次迭代，当且仅当频率点数为400点时，标准差Sσ处于阀值界定线之下，即模型修正收敛。

表2　支架模型修正参数对比表

**200点　oo 400点　△△600点　++800点　∙∙1 000点——标准差0.03阀值界定线图6迭代变化图

400点频响函数残差法修正后的模型频响函数相关系数期望ϕ1=1.05×10-17，ϕ2=0.001 8，根据式（18）可知满足判定准则。

测点频响函数仿真与测试值对比如图7所示。

图7　修正模型频响函数与试验频响函数对比

由图7可知，采用频响函数残差法，当其点数为400时，修正后模型频响函数与测试频响函数吻合。

综上，合适的频率点数可以提高频响函数残差法对有限元模型修正的效率。

3.2频带范围

由于实际测试的频响频带宽度有限［13］，而过窄频带的频响函数则不能准确描述结构的动态特性，此处研究频带范围在0～10 Hz、0～50 Hz、0～75 Hz、0～100 Hz和0～120 Hz工况下（频响函数均取400点）支架模型修正效果的变化规律。

标准差Sσ2随迭代次数变化如图8所示（Sσ1数量级均为10-16，满足判定准则，故不再画出）。

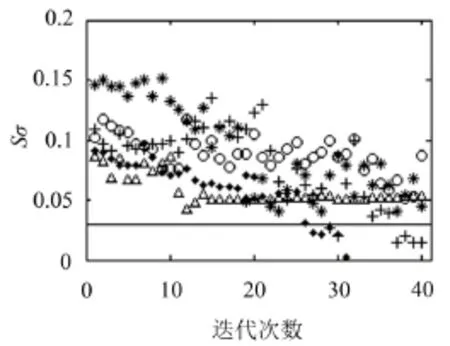
图8　迭代变化图

由图8可知，截止40次迭代，当频带范围为0～100 Hz和0～120 Hz时，Sσ处于阀值界定线之下，模型修正收敛。且0～100 Hz达到收敛精度需要40次迭代，0～120 Hz需要31次。

0～100 Hz和0～120 Hz频响函数残差法修正后的模型频响函数相关系数期望为：

0～100 Hz：ϕ1=1.05×10-17，ϕ2=0.001 8，

0～120 Hz：ϕ1=3.03×10-17，ϕ2=0.000 2，

根据式（18）可知均满足判定准则。

测点频响函数与试验频响函数对比如图9所示。

图9　修正模型频响函数与试验频响函数对比

由图7可知，采用频响函数残差法，当其频带范围为0～100 Hz和0～120 Hz时，修正后模型频响函数与测试频响函数吻合。

综上，参与修正的频带范围越宽，频响函数残差法模型修正的效率越高。

4　结语

（1）基于频响函数相关系数的期望和标准差建立模型精度判定准则，对比了频响函数相关性法和频响函数残差法对支架有限元模型的修正效果。

（2）利用频响函数相关性法修正模型出现振荡不收敛；利用频响函数残差法修正支架模型最大误差仅为0.36%，表明频响函数残差法的有效性与实用性。

（3）通过对比200点、400点、600点、800点和1 000点频响函数残差法对模型进行修正，400点频响函数最易达到修正目标。因此，选取合适的频率点数可以提高频响函数残差法对有限元模型修正的效率。

（4）通过对比0～100 Hz和0～120 Hz频响函数残差法对模型进行修正，0～120 Hz频响函数较0～100 Hz更快达到预设的精度判定准则。因此，较宽的频带范围有利于频响函数残差法模型修正效率的提高。

［1］董宗鹏，章艺.基于频响函数灵敏度分析的舰艇模型修正［J］.上海交通大学学报，2005，39（11）：1848-1850.

［2］黄修长，徐时吟.基于频响函数综合的舱筏隔振系统灵敏度分析和优化［J］.振动与冲击，2011，30（5）：145-151.

［3］李效法.基于灵敏度分析的模型修正研究及其实现［D］.南京：南京航空航天大学，2007.

［4］邱飞力，张立民.支架结构建模中设计参数的修正与优化［J］.噪声与振动控制，2014，34（1）：36-40.

［5］丁继锋，韩增尧.基于频响函数模型修正影响因素的仿真［J］.中国空间科学技术，2010，（5）：2-8.

［6］LIN R M，ZH U J.Model updating of damped structures using FRF data［J］.Mechanical Systems and Signal Processing，2006，20:2200-2218.

［7］徐张明，沈荣瀛.基于频响函数相关性的灵敏度分析的有限元模型修正［J］.机械强度，2003，25（1）：5-8.

［8］温华兵，王国治基于频响函数相关系数灵敏度的浮筏舱段有限元模型修正［J］.江苏科技大学学报（自然科学版），2005，19（6）：75-78.

［9］曹昭.关于独立随机变量和的期望与方差性质的运用［J］.方法应用，2014，（4）：81-83.

［10］傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000：33-38.

［11］LINK M.Updating analytical models by using local and global parameters and relaxed optimisation requirements［J］.Mechanical Systems and Signal Processing，1998，12（1）:7-22.

［12］邱飞力，张立民.Tikhonov方法在不适定模型修正中的应用［J］.振动与冲击，2015，34（12）：121-126.

［13］于金朋，邱飞力.基于冲击激励的支架结构参数研究［J］.北方交通大学学报，2001，35（6）：98-101.

Application of FRF Residual-error Method in Finite Element Model Updating

QU Jing-jing，ZHANG Li-min，QIU Fei-li，ZHOUHui

（State Key Laboratory of Traction Power，Southwest Jiaotong University，Chengdu 610031，China）

Dynamic information of actual structures can be reflected by accurate finite element models effectively.In order to reduce the error in structural modeling，it is necessary to update the finite element model.Currently，the updating methods based on modal frequencies，mode shapes and FRF have been used widely.Among them，the method based on FRF has more advantages than the others since it can avoid the error from modal parameters identification and its testing DOF is unlimited.According to the objective function，the method based on FRF can be classified into FRF correlation method and FRF residual-error method.The FRF correlation method is based on the correlation of mode shape and amplitude with parameters sensitivity.However，in comparison with the FRF residual-error method，this method loses the direct correlation between the FRF and design parameters so that the oscillation and divergence phenomena occur in the model updating for some structures.Therefore，with an actual structure as the object，the two methods in the finite element model updating are compared each other；and the effect of the frequency points and frequency range on the model updating based on FRF residual-error method is analyzed.The results show that the residual-error method can lead to a stable convergence and it has high efficiency.Meanwhile，reasonable frequency points and wider frequency range are beneficial to improving the updating efficiency.

vibration and wave；model updating；FRF-sensitivity；frequency points；frequency range

O327

ADOI编码：10.3969/j.issn.1006-1335.2016.04.011

1006-1355（2016）04-0053-05

2015-12-23

屈晶晶（1992-），女，重庆潼南人，硕士研究生，主要研究方向为有限元模型修正、高速动车组减振降噪设计。E-mail:675876357@qq.com