正交各向异性功能梯度材料平板振动分析

徐　坤，陈美霞，谢　坤

（华中科技大学 船舶与海洋工程学院，武汉 430074）



正交各向异性功能梯度材料平板振动分析

徐坤，陈美霞，谢坤

（华中科技大学 船舶与海洋工程学院，武汉 430074）

基于一阶剪切理论，研究四边简支正交各向异性功能梯度材料（FGM）板的自由振动和受迫振动。假设剪应力沿厚度方向呈抛物线分布，利用剪切应变能与剪切余能相等原理，得到正交各向异性功能梯度平板的剪切修正系数。利用虚位移原理得到功能梯度平板运动方程，并采用Navier方法对运动方程进行求解。通过与有关文献及有限元计算结果对比，验证该方法的正确性。在此基础上，分析厚度方向上由纤维和基体按照不同体积梯度分布的三种（P-，S-，C-FGM）平板的固有振动和受激振动特性，结果表明纤维体积分数变化区间越大，梯度型式及梯度指数对其振动特性影响越显著；纤维体积分数关于平板中面反对称分布（S-FGM）时，平板振动特性受梯度指数影响较小。

振动与波；功能梯度材料；一阶剪切理论；剪切修正系数

功能梯度材料（FGM）是一种新型复合材料，其具有空间连续梯度变化的微观结构，可引起材料属性的梯度变化。功能梯度材料板相比层合板消除了材料连接处的宏观界面，实现了材料内部功能的渐变，具有缓和热应力、避免或降低层间应力集中等优点。此外，功能梯度材料具有良好的可设计性，可通过合理设计来改变材料的组成及梯度变化形式，实现不同功能的组合和优良的力学特性。

目前，功能梯度材料板壳的弯曲和振动问题研究与层合板［1-2］类似，主要有基于板理论的解析方法以及有限元方法等。Chi等［3-4］根据经典板理论和Fourier级数展开，分析了功能梯度平板弯曲问题，认为功能梯度平板弯曲刚度不同于均质板，是关于材料参数分布的复杂组合。曹志远［5］和Loy［6］采用经典板理论分别分析了矩形平板和简支功能梯度材料圆柱壳的固有频率。Nguyen［7］基于1阶剪切变形理论，分析了功能梯度材料平板的弯曲问题。Reddy［8］和Akbarzadeh［9］基于3阶剪切变形理论，分别得到了功能梯度平板的理论方程，以及通过Fourier级数展开和Laplace变换，分析了梯度平板在动载荷作用下的响应。Ferreira［10］基于1阶、3阶剪切变形理论及MQ径向基函数分析了功能梯度板的自由振动。Qian［11］基于高阶剪切变形理论及局部彼得洛夫-伽辽金法分析了功能梯度平板的静力及动力变形问题。对于功能梯度材料夹芯板，李华东［12］将位移和横向剪力用三角级数展开，研究了四边简支功能梯度夹层板的自由振动问题。

由于工艺等条件的限制，实际的功能梯度材料很少是各向同性的，而是大多表现出正交各向异性［13］。Ramirez［14］采用离散分层理论结合Ritz法分析了各向异性功能梯度板的弯曲问题。Batra［15］基于1阶剪切变性理论及有限元法，分析了纤维铺角对各向异性功能梯度平板固有频率的影响。Zhang［16］基于3阶剪切变形理论，分析了正交各向异性功能梯度平板的非线性振动问题。陈伟球［17］通过引入位移函数和应力函数，结合分层近似理论分析了横观各向同性功能梯度材料板的自由振动。

文献［3-11］的研究对象主要为各向同性材料功能梯度板，而且大都只假设材料的杨氏模量在厚度方向上梯度变化，未考虑梯度材料中密度等其他材料参数变化。此外，采用1阶剪切变形理论求解功能梯度平板的振动问题同高阶方法［8-16］相比，不仅具有足够的精度［17］，且公式中变量的物理意义明确、步骤更加简便、求解效率更高。

文中基于1阶剪切变形理论，假设了剪力沿厚度方向上的分布形式，导出了正交各项异性功能梯度板的剪切修正系数计算式及四边简支功能梯度平板自由振动及受迫振动的理论公式，并分析了不同组分体积梯度分布的三种（P-，S-，C-FGM）正交各向异性功能梯度平板的自由振动和受迫振动。

1　基本公式

考察受到横向载荷作用且材料参数沿厚度方向变化的正交各向异性梯度材料矩形板。图1是一种由纤维和基体在厚度方向上按照不同比例混合得到的正交各项异性梯度平板。由于厚度方向上组分体积分数梯度变化，平板沿厚度方向材料参数呈现梯度变化。此外，增强纤维的方向性使得平板呈正交各向异性。假设平板等厚度，平板材料弹性主轴方向与图1中平板分析坐标系一致，板长为a，宽为b，厚度为h。

根据平板1阶剪切变形的假设［18］，平板内任意一点的位移为

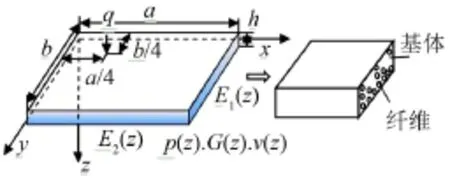
图1　纤维与基体梯度混合的功能梯度平板

沿厚度方向的剪应变为

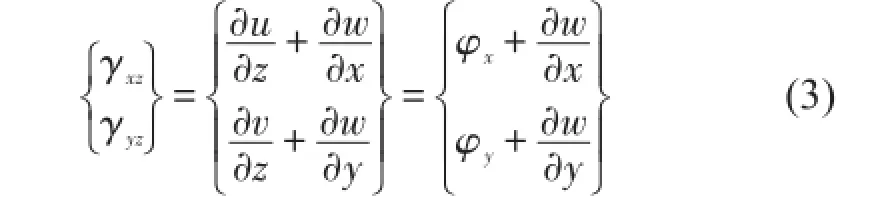
在1阶变形假设下，板的应力应变关系满足

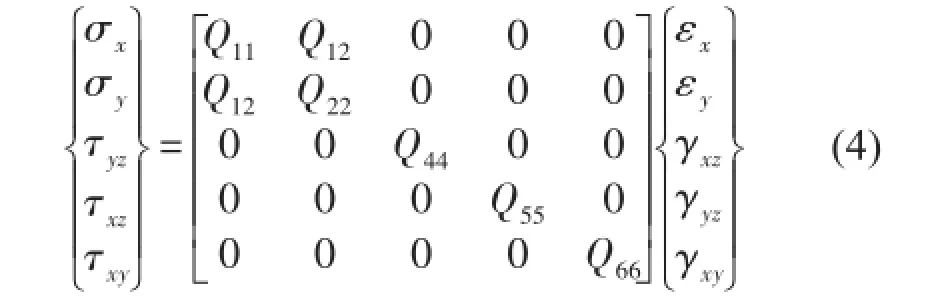
式中Q11、Q12、Q22、Q44、Q55、Q66分别为板厚方向上的刚度系数，计算公式［18］为

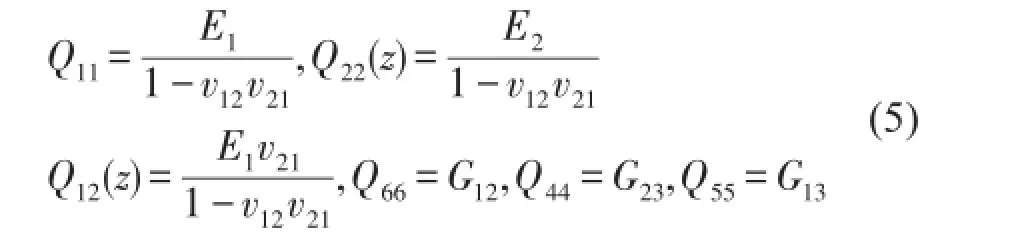
G12、G13、G23为材料的剪切模量。截面合力N=（Nx，Ny，Nxy）T及截面弯矩M=（Mx，My，Mxy）T为

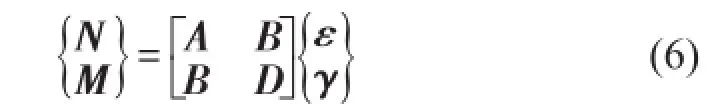
其中

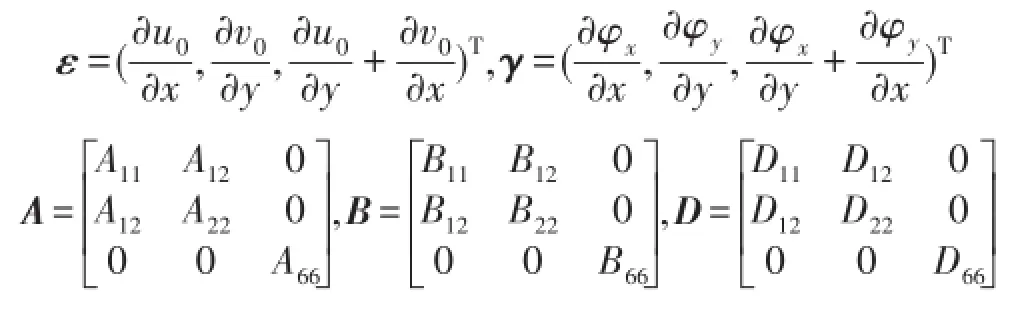
矩阵元素Aij，Bij是关于Qij及厚度方向坐标z的积分，表达式分别为

由于梯度材料平板的材料参数沿板厚方向呈梯度变化，沿厚度方向的剪切变形不能忽略。采用1阶剪切变形假设分析功能梯度材料平板的动力学问题时，由于广义胡克定律和横向剪切刚度为有限值，该假设下横向剪应力沿厚度方向均匀分布，这与平板上下表面剪应力为零的边界条件相矛盾，为了解决这个矛盾，需要对剪切系数进行修正［18］。这里对文献［19］中的剪力分布假设进行扩展，假设梯度材料平板截面厚度方向上的应力分布与均匀材料梁的剪应力分布类似，即假设沿厚度h方向的平板截面的剪应力有式（8）中的抛物线型的分布形式

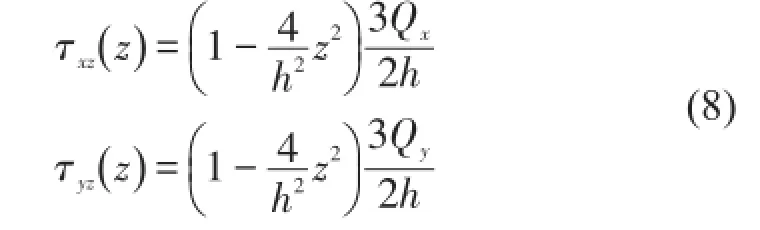
其中Qx和Qy分别为平板垂直于x和y单位长度截面上的剪力的合力。由于功能梯度平板材料厚度方向上的梯度变化，实际剪应力一般不再呈抛物线型式分布，但工程上采用该抛物线分布假设分析梯度平板得到的结果有足够精度。根据剪切余能的定义，单位面积功能梯度板的剪切余应变能为

将式（8）代入式（9），得到应变能的表达式

假设C44、C55为修正后的剪切刚度，用C44、C55表示功能梯度平板的剪切余应变能密度为

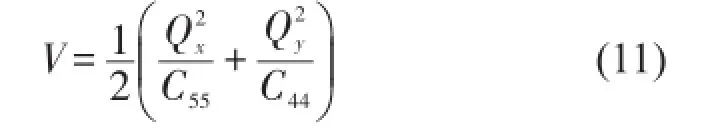
按照剪切余应变能密度相等得到

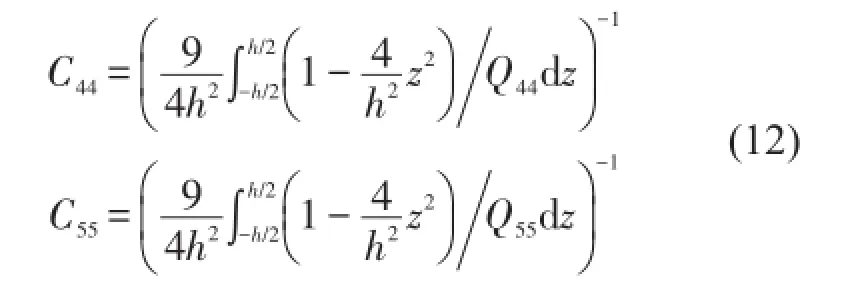
修正前单位长度截面剪力表达式为

修正后的截面剪力的表达式为

由剪切修正系数的定义，得到剪切修正系数为

由式（15）可知，功能梯度材料平板的剪切修正系数是关于假设的剪应力分布函数以及功能梯度平板厚度方向的材料剪切模量的分布函数共同作用的表达式，在已知材料剪切模量分布的情况下，通过式（15）得到功能梯度平板修正后的剪切刚度。

根据虚位移原理，类比层合板的振动平衡方程［16］，得到功能梯度平板的动力学方程为

对于四边简支功能梯度板，平衡方程可采用双三角级数方法求解［18］，假设功能梯度平板的位移满足式（18）中的双三角级数表达式

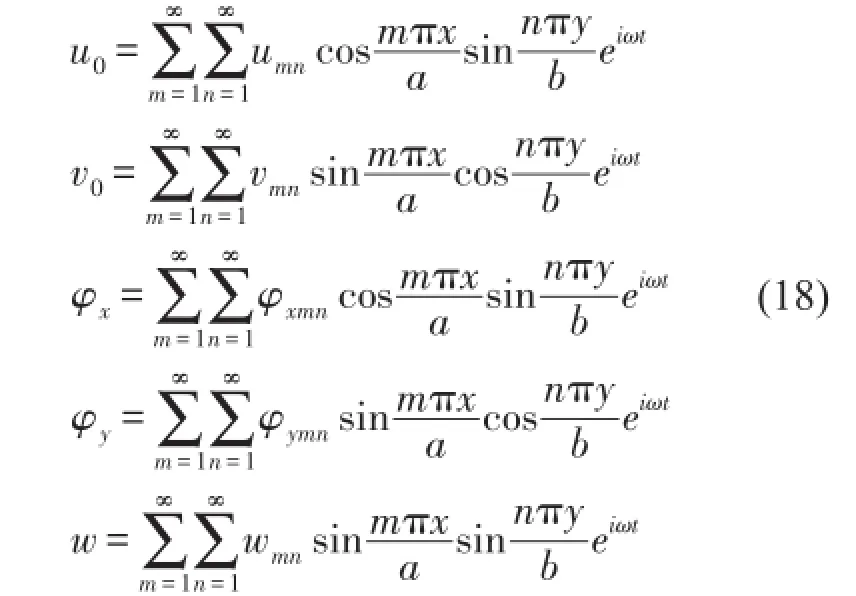
其中umn、νmn、φxmn、φymn和wmn为广义位移幅值，式中的m和n分别为平板振动时在x方向及y方向的半波数。同样，将横向载荷展开成

截取位移函数表达式（18）前N项，代入平衡方程（16）中，并在平衡方程等式两边分别乘上对应的三角函数表达式，利用三角函数正交性解耦，得到关于广义位移幅值的线性方程组

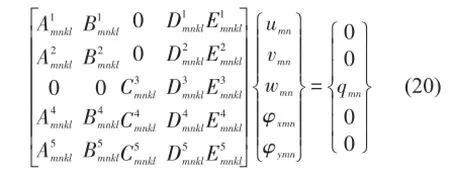
其中m，n，k，l=1，2…N，等式左边是关于广义位移为未知变量的线性组合，等式右边为横向载荷广义力。求解得到功能梯度平板各个广义位移幅值，得到平板在横向力作用下的响应。

对于功能梯度平板的固有频率，令qmn=0，由任意阶振型（m，n）下广义位移幅值不全为零，由式（21）系数矩阵的行列式为零，可得对应振型下的功能梯度板固有频率值。

其中系数矩阵中的各元素即为平衡方程式（16）中对应振型广义位移幅值的系数。

2　数值分析

2.1方法验证

首先将本文方法的结果同文献［20］各向同性功能梯度材料平板的固有频率进行对比，如表1所示（无量纲化及p见文献［20］）。本文方法结果同文献结果差别较小，表明本方法能够较准确退化分析各向同性功能梯度材料的固有振动。

对于正交各向异性功能梯度板，考察图1所示的纤维和基体沿平板厚度方向按照一定梯度变化的比例混合而成的简支平板，板长a=1.2 m，板宽b= 0.8 m，厚0.02 m。在平板厚度方向材料参数与纤维和基体的比例存在如式（22）的关系［19］。

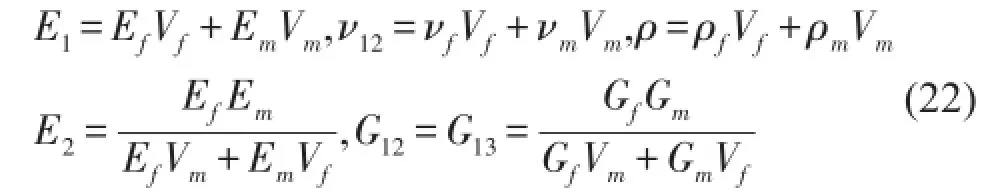
其中E1为梯度板纵向杨氏模量，E2为横向杨氏模量，ν12为主泊松比，G12为剪切模量。假设G23=G12，Gf和Gm分别为纤维和基体的剪切模量，纤维和基体均为各向同性材料，取纤维杨氏模量Ef=72 000 Mpa，基体杨氏模量Em=6 900 Mpa，纤维泊松比νf=0.22，基体的泊松比νm=0.4，纤维的密度ρf=2 500 kg/m3，基体的密度ρm=1 200 kg/m3，且剪切模量满足式（22）中的关系。

假设基体材料体积分数Vm沿厚度方向呈梯度变化，且存在式（24）中的P、S、C三种型式的体积分数分布函数

S分布：

三种分布型式的表达式（24）中，V1、V2分别是功能梯度平板中基体体积分数Vm的最小值和最大值。特别地，对于P、C两种分布，V1、V2分别为功能梯度平板下表面和上表面处的基体体积分数。式（27）中的指数γ选取不同的值，基体体积分数Vm的曲线也会呈现不同的变化趋势，称γ为梯度指数。图2是V1=0.25，V2=0.75时，P、S、C三种分布型式功能梯度板厚度方向Vm随γ变化曲线。

如图2（a），P型分布下功能梯度平板厚度方向上基体材料的组分呈现幂律变化，梯度指数较大或较小时，基体体积分数会在平板一侧表面出现较大梯度的变化。S型分布情况下，基体体积分数曲线关于平板中面呈类似“S”反对称分布，C型分布情况基体材料体积分数关于平板中面对称。

分别计算P分布形式下不同γ值下梯度平板的固有频率，并将固有频率同有限元方法结果进行对比。鉴于目前尚没有功能梯度材料有限元分析的商用软件，采用层合平板来近似等效功能梯度平板，即在有限元建模中，将梯度平板沿厚度方向上离散分成多层，每一层视为均匀材料，各相邻层之间实现材料参数阶梯变化，来近似模拟材料参数沿厚度方向上的连续的梯度变化。文中分层数为20时有限元结果已收敛，故有限元模型均采用20层等效。通过有限元方法同本文方法的对比验证本文方法的正确性。表2是本文方法与有限元方法计算功能梯度板不同振型对应的固有频率结果对比。

表1　不同厚宽比及p值下Al/ZrO2功能梯度方板基频对比

为验证梯度平板动响应分析正确性，计算梯度平板在受到点力作用下的频响。激励力作用于距离平板长边和短边各1/4处，如图1，方向垂直于板平面，大小为1 N。图3（a）和图3（b）分别是本文方法与有限元方法计算P分布下激励点速度频响和平板均方振速的对比曲线。

模态分析和谐响应分析结果表明1阶剪切方法与有限元方法吻合得较好，本文方法适用于梯度平板的动力学分析。

2.2功能梯度平板固有振动分析

对2.1中的模型，当V1=0.25，V2=0.75时P、S、C梯度型式平板的基频随γ变化如图4。

由图4可知，P、C分布梯度平板的基频随着梯度指数γ的增加而增大。这是由于γ越大，富含纤维的材料沿厚度方向的分布范围越大。纤维的杨氏模量比基体的杨氏模量相比要大很多，两者按照比例混合后，纤维的体积分数主要决定了梯度平板的刚度。纤维丰度高的材料沿厚度方向的分布范围越大，平板的刚度也就越大，相应振型的固有频率也就越高。对于S分布梯度板，随着梯度指数变化，关于中面对称的位置纤维体积分数总是呈现相反的变化，板的质量及刚度变化较小，因此γ对其固有振动特性影响不大。

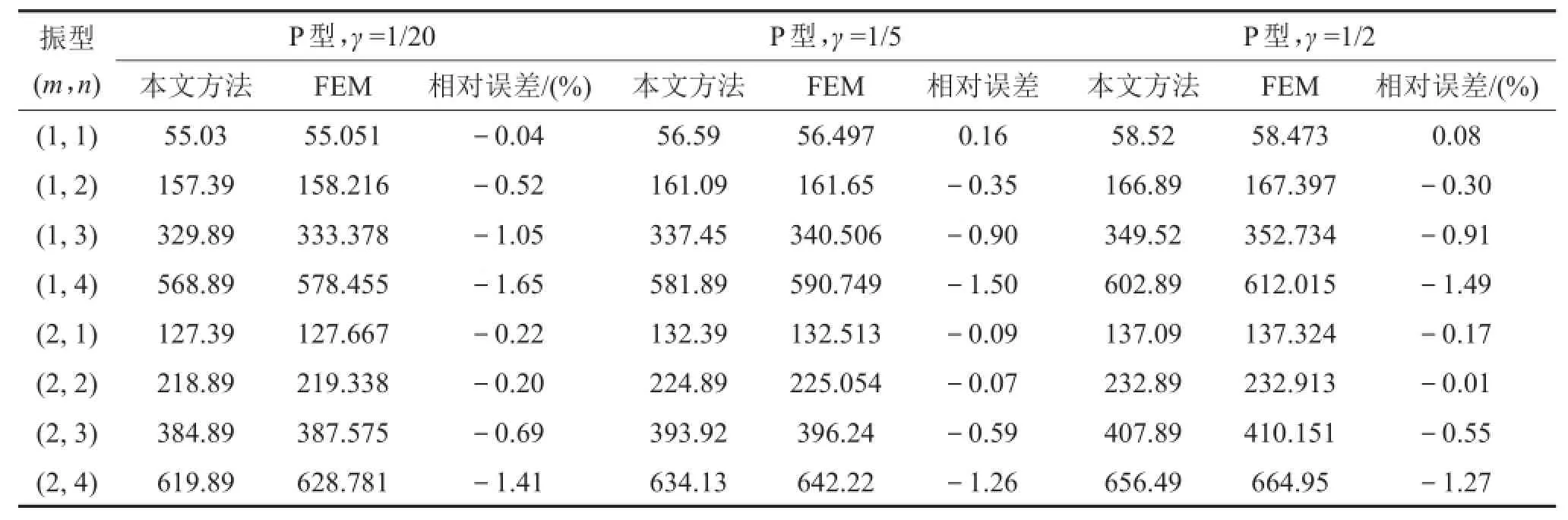
表2　功能梯度板各阶振型固有频率同有限元结果对比

图2　不同梯度指数γ下基体体积分数的分布曲线

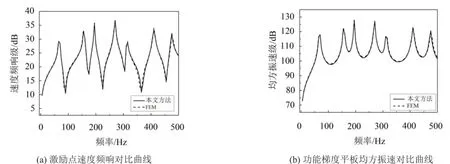
图3　本文方法与有限元结果对比

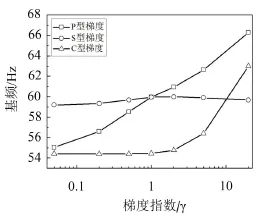
图4　功能梯度板基频随梯度指数变化曲线

图5（a）—图5（c）所示的是V1和V2取不同组合时P、S、C梯度型式平板基频随γ的变化曲线。

由图5（a）可知，P分布功能梯度平板的基频总是随着梯度指数的增加而增大，且（V2-V1）的差值越大，这种增加的趋势越明显。由图5（b）可知，对于S型分布功能梯度平板，基频随着梯度指数的增加先增大，后减小。由图5（c）可知，对于C型分布梯度平板，（V2-V1）对基频的影响同P分布具有类似的规律。P、S分布中，（V2-V1）决定了平板上下两个表面基体材料体积分数的差异，这表明功能梯度材料平板两侧材料差异越小，梯度指数对基频的影响越小。C分布中，（V2-V1）决定了功能梯度材料板厚度中心位置与上下表面的基体材料体积的差异，这种差异越小，γ对基频的影响越小。

2.3功能梯度平板受迫振动分析

对2.1中的模型，分析平板在点力作用下的均方振速，图6（a）—图6（c）是不同γ值下平板均方振速。

由图6（a）可知，P型分布梯度平板的均方振速峰值频率随着γ值的增加而增大，这与平板固有频率随γ的变化规律一致。此外，大部分频率下均方振速随着γ值的增大而减小，这与平板中纤维体积分数增加，刚度有所增加有关。由图6（b）可知，S分布梯度板的均方振速变化随γ变化并不明显，这是由于平板的材料参数总是关于平板的中面呈现相反规律的变化，对平板的振动特性影响起到了相互削减的作用。由图6（c）可知，当γ=1与γ=1/5时梯度平板的均方振速差异较小，若P继续增加，当γ=5时，平板的均方振速峰值频率增大，且大部分频率下均方振速水平有所下降。这是由于γ＜1时，材料参数随γ的变化并不明显，均方振速随γ变化不大。γ从1到5，厚度方向上纤维的比例显著增加，使得均方振速水平有所降低。

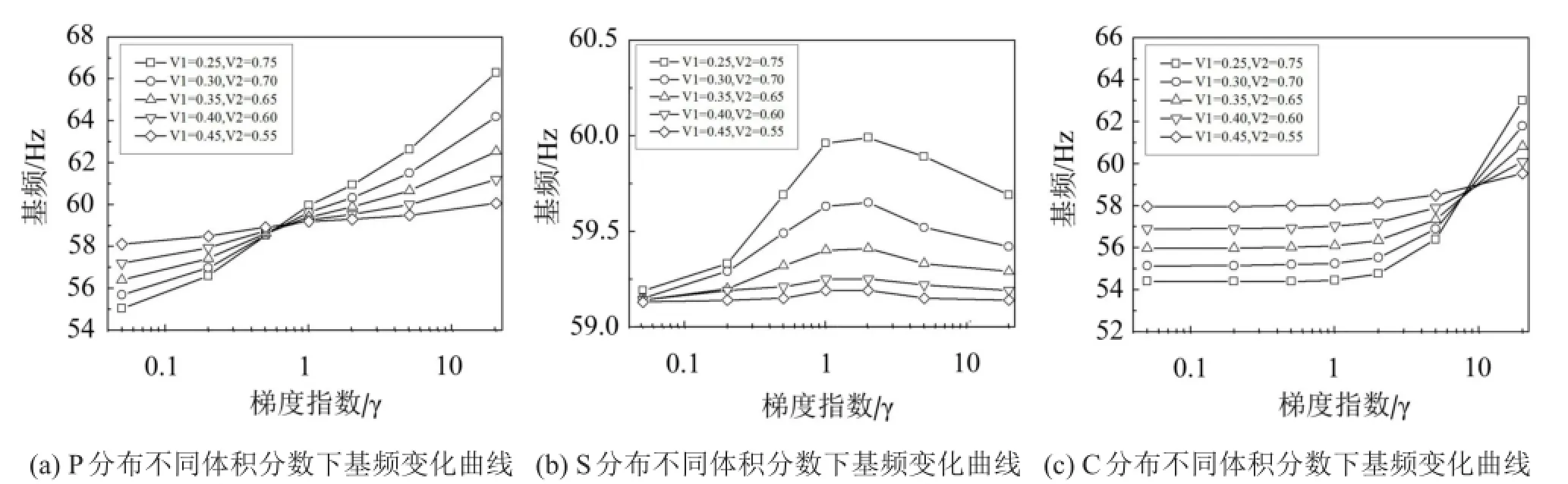
图5　平板基频随体积分数变化曲线

图6　功能梯度板均方振速随梯度指数变化曲线

3　结语

基于1阶剪切理论得到简支正交各向异性梯度平板的自由振动及受横向载荷激励下的谐响应分析方法，通过对特定体积梯度混合得到的正交各向异性梯度复合材料平板的振动特性的数值分析，可以得到以下结论：

（1）采用1阶剪切方法分析正交各向异性功能梯度平板的振动特性，通过与有限元方法的对比，表明本文方法具有较高的精度，利用该方法能够较准确地分析功能梯度材料平板的固有振动和受迫振动问题；

（2）功能梯度材料平板的固有振动特性受到组分材料体积分数变化区间、梯度型式、梯度指数等因素的综合影响。平板中纤维的体积分数的变化区间越大，梯度型式及梯度指数对其振动特性影响作用越显著。当纤维材料的体积分数变化区间一定时，类似S型反对称分布型式的平板受到梯度指数的影响较小，而幂律（P-）及对称分布型式（C-）功能梯度平板的振动特性受梯度指数的影响较大；

（3）功能梯度材料平板的受迫振动特性受到组分体积分数、梯度型式以及梯度指数的影响，影响规律同固有振动特性规律一致，表现为平板厚度上纤维分布范围越大，平板刚度变大，均方振速有减小的趋势。

［1］胡昊灏，商德江.复合层合矩形板水下声辐射解析计算［J］.噪声与振动控制，2014，01：205-208+217.

［2］赵飞，吴锦武，赵龙胜.采用分层理论计算层合板的固有频率和振型［J］.噪声与振动控制，2014，02：34-40.

［3］ CHI S H，CHUNG Y L.Mechanical behavior of functionally graded material plates under transverse load-Part I:Analysis［J］.International Journal of Solids and Structures，2006，43（13）:3657-3674.

［4］ CHI S H，CHUNG Y L.Mechanical behavior of functionally graded material plates under transverse loadpart II:numerical results［J］.International Journal of Solids and Structures，2006，43（13）:3675-3691.

［5］曹志远.不同边界条件功能梯度矩形板固有频率解的一般表达式［J］.复合材料学报，2005，22（5）：172-177.

［6］ LOY C T，LAM K Y，REDDY J N.Vibration of functionally graded cylindrical shells［J］.International Journal of Mechanical Sciences，1999，41（3）:309-324.

［7］NGUYEN T K，SAB K，BONNET G.First-order shear deformation plate models for functionally graded materials［J］.Composite Structures，2008，83（1）:25-36.

［8］REDDY J N.Analysis of functionally graded plates［J］. InternationalJournalforNumericalMethodsin Engineering，2000，47（1-3）:663-684.

［9］AKBARZADEH A H，ZAD S K H，ESLAMI M R，et al. Mechanical behaviour of functionally graded plates under staticanddynamicloading［C］.Proceedingsofthe Institution of Mechanical Engineers，Part C:Journal of Mechanical Engineering Science，2011，225（2）:326-333.

［10］FERREIRA A J M，BATRA R C，ROQUE C M C，et al. Natural frequencies of functionally graded plates by a meshless method［J］.Composite Structures，2006，75（8）: 593-600.

［11］QIAN L F，BATRA R C，CHEN L M.Static and dynamic deformations of thick functionally graded elastic plates by using higher-order shear and normal deformable plate theory and meshless local Petrov-Galerkin method［J］. Composites Part B Engineering，2004，35:685-697.

［12］李华东，朱锡，梅志远，等.正交各向异性功能梯度夹层板的自由振动分析［J］.哈尔滨工程大学学报，2014，（3）.

［13］马力，吴林志.各向异性功能梯度材料中裂纹对弹性波的散射［C］.中国力学学会学术大会 2005论文摘要集（下），2005.

［14］RAMIREZ F，HEYLIGER P R，PAN E.Static analysis of functionally graded elastic anisotropic plates using a discretelayerapproach［J］.CompositesPartB Engineering，2006，37（1）:10-20.

［15］BATRA R C，JIN J.Natural frequencies of a functionally graded anisotropic rectangular plate［J］.Journal of Sound &Vibration，2005，282（1-2）:509-516.

［16］ZHANG W，YANG J，HAO Y.Chaotic vibrations of an orthotropic FGM rectangular plate based on third-order shear deformation theory［J］.Nonlinear Dynamics，2010，59（4）:619-660.

［17］陈伟球，叶贵如.横观各向同性功能梯度材料矩形板的自由振动［J］.振动工程学报，2001，14（3）：263-267.

［18］Reddy J N.Mechanics of laminated composite plates and shells:theory and analysis［M］.CRC press，2004.

［19］王震鸣，刘国玺，吕明身.各向异性多层扁壳的大挠度方程［J］.应用数学和力学，1982，3（1）：49-65.

［20］FERREIRA A J M，BATRA R C，ROQUE C M C，et al. Natural frequencies of functionally graded plates by a meshless method［J］.Composite Structures，2006，75（8）: 593-600.

VibrationAnalysis of Orthotropic Functionally Graded Plates

XUKun，CHEN Mei-xia，XIEKun

（School of NavalArchitecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China）

Based on the first order shear deformation theory（FSDT），free and forced vibrations of orthotropic functionally graded material（FGM）plates with simply supported boundary conditions are analyzed.Utilizing the principle of shear strain energy and assuming that the shear stress distribution has the parabola form across the plate thickness，the shear correction coefficient of the orthotropic FGM plate is obtained.The dynamic equations of the plate are deduced by the principle of virtual displacement and solved by the Navier’s double Fourier series method.The present method is verified by finite element solutions.On this basis，the free and forced vibration characteristics of the plates with three different functional gradient types indicated by P-，S-and C-FGM respectively，are obtained and analyzed.These different functional gradients across the thickness of the plate are realized by different fibre-to-matrix volume ratios.The results show that the effects of gradient type and gradient exponent on FGM plates’vibration characteristics are more obvious when the volume fraction of the fibre varies in a larger range.The gradient exponent has little effect when the volume fraction of the fibre is antisymmetrically distributed（indicated by S-FGM）across the plate thickness.

vibration and wave；functionally graded material；first order shear deformation theory（FSDT）；shear correction coefficient

O327

ADOI编码：10.3969/j.issn.1006-1335.2016.04.003

1006-1355（2016）04-0014-07

2016-01-02

国家自然科学基金资助项目（51179071）

徐坤（1989-），男，湖北省随州市人，硕士生，主要研究方向为振动与噪声控制。

陈美霞，女，硕士生导师。E-mail:chenmx26@hust.edu.cn