ASAC系统中少测点条件下的近场声压误差传感策略
苏常伟,朱海潮,毛荣富,苏俊博
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033)
振动理论与数值解法
ASAC系统中少测点条件下的近场声压误差传感策略
苏常伟1,2,朱海潮1,2,毛荣富1,2,苏俊博1,2
(1.海军工程大学 振动与噪声研究所,武汉 430033;2.船舶振动噪声重点实验室,武汉 430033)
根据有源控制策略设计简洁、有效的误差传感非常关键。针对基于声压声辐射模态的有源控制策略,具体设计与之对应的少测点条件下近场声压误差传感策略。首先,通过分析声压声辐射模态的空间滤波特性,证明基于声压声辐射模态的有源控制策略可行;然后,利用近场测量面上有限个测点的声压分布,通过求解模态展开所构成的欠定方程组的最小模最小二乘解,获取前K阶声压声辐射模态伴随系数的近似值,从而形成与基于声压声辐射模态的有源控制策略相对应的近场声压误差传感策略;最后,以置于无限大障板上的钢质简支薄板为例,进行数值仿真分析。结果表明设计的误差传感策略可行,所获得的前K阶声压声辐射模态伴随系数具有较高的精度。
声学;误差传感;近场声压;声压声辐射模态;有源结构声控制;少测点
近年来,为了有效控制振动结构低频辐射噪声,有源结构声控制(Active structural acoustic control,ASAC)技术受到了人们广泛关注。在ASAC系统中,根据有源控制策略设计简洁、有效的误差传感非常关键。所谓误差传感策略,是指在控制系统中获取误差信号的方法和手段。良好的误差传感策略既可采集到对辐射声功率起主要作用的信息,有效实施有源控制策略,又可避免控制器处理过多输入信息而导致运算能力下降[1]。传统的ASAC系统采用位于远场的声学传感器检测声学量(如场点声压)作为误差信号,构成系统的目标函数,这在实际应用中受到一些限制,不仅难以获得全局控制效果,而且会由于结构作动器和传感器之间存在“时延”而导致控制效果不佳。
Borgiotti等学者在90年代初期提出声辐射模态的概念,并指出声辐射模态的重要特性:每阶声辐射模态单独辐射声功率[2]。由此,一种基于声辐射模态的有源控制策略应运而生,即只要控制有限的几阶主导辐射模态的声功率,就能有效地控制结构的低频辐射噪声,这使得有源结构声控制的实现大为简便。根据声功率表达式中参量形式不同,声辐射模态可分为振速声辐射模态、声压声辐射模态、源强(源强密度)声辐射模态和力声辐射模态等。目前,国内外学者普遍选用结构表面振速声辐射模态进行该有源控制策略的研究,其对应的误差传感策略关键在于采集到对声功率起主要贡献的几阶主导振速声辐射模态信息。已知梁、板等简单结构在中、低频时的主导辐射模态即为其前几阶声辐射模态。TANAKA等使用聚偏氟乙烯(Polyvinylidene fluoride,PVDF)压电传感器测量简支板的振速声辐射模态[3]。吴锦武、李双等则对利用PVDF压电薄膜测量平板结构前几阶振速声辐射模态伴随系数进行了深入研究[4-5]。然而,虽然通过设计PVDF压电薄膜形状可以测量声辐射模态伴随系数,但要同时获得前几阶声辐射模态伴随系数所需要的PVDF薄膜个数非常多,阶次越高薄膜形状越复杂,且PVDF传感器的设计受到振动结构边界条件的限制,这会在实际应用中带来不便。吴锦武、姜哲等提出可在振动结构上测量有限个点的振动速度分布,通过求解欠定方程组得到前几阶振速声辐射模态伴随系数近似值,这种直接测量结构表面振速的方法在实验中较为常用[6]。然而,对于一些对安装传感器比较敏感的振动结构,该方法便不再适用,比如:
(1)非常薄的振动结构(比如薄板、薄壳等),它们对外界附加质量非常敏感,测点阵列的安装不可避免地会改变其振速场,从而导致有源控制策略无法有效实施;
(2)在实际应用中,在一些结构表面布置传感器阵列存在极大困难,同时布置位置也会受到各种条件的限制。
陈克安等为了解决有源声学结构中误差信息的传感问题,推导了基于近场声压的辐射声功率计算公式,指出利用近场声压作为误差信息可以实现结构声辐射的有源控制[7]。这就为安装传感器阵列比较敏感的振动结构提供了一个可行的误差传感途径。然而,对于如何利用近场声压数据具体设计可以获得全局控制效果、易于工程实现且适用于敏感结构的误差传感策略,文献[7]并没有开展具体研究及验证。本文从声压声辐射模态出发,具体设计了一种少测点条件下的近场声压误差传感策略,并对其有效性和可行性进行数值仿真验证,后续研究中还将开展测点布置优化研究以实现更少测点、更高精度。
1 基于声压声辐射模态的有源控制策略
目前,国内外学者对振速声辐射模态进行了全面且深入的研究,而对声压声辐射模态的研究还比较少。本文首先讨论声压声辐射模态的空间滤波特性,论证基于声压声辐射模态的有源控制策略是否可行。
和振速声辐射模态的求解方法类似,文献[8]给出了声压声辐射模态的基本算法,这里不再赘述。振动结构表面的声压可以表示为各阶声压声辐射模态叠加的形式

其中P为结构离散后由表面声压组成的N维列向量;Φ为N×N维矩阵,其列向量φi为结构的声压声辐射模态,模态之间相互正交;ci=φiTP为第i阶声压声辐射模态伴随系数,c为由ci组成的N维列向量;N为离散单元数目。
振动结构的辐射声功率可写为

其中λi(i=1,2,…N)为每阶声压声辐射模态对应的特征值,从物理意义上讲,λi与各阶模态的声辐射效率成正比。
接下来建立声压声辐射模态频域和空间波数域的联系,用于分析声压声辐射模态的空间滤波特性。以一置于无限障板上的正方形简支平板为例,取边长L=0.5 m。将平板离散为25×25个等面积单元,图1为平板在频率为380 Hz时的前6阶声压声辐射模态,图2给出了图1中平板的前六阶声压声辐射模态对应的波数域谱。由图2可见,此频率下传播波成分主要集中在前几阶模态中。分析低频其它频率,可得到相同结论。因此,在低频时平板的声压声辐射模态具有明显的空间滤波特性,即前几阶声压声辐射模态辐射的声功率占结构总声功率的绝大部分。由此可得,控制前几阶声压声辐射模态即可有效控制结构的远场声辐射,即基于声压声辐射模态的有源控制策略是可行的。
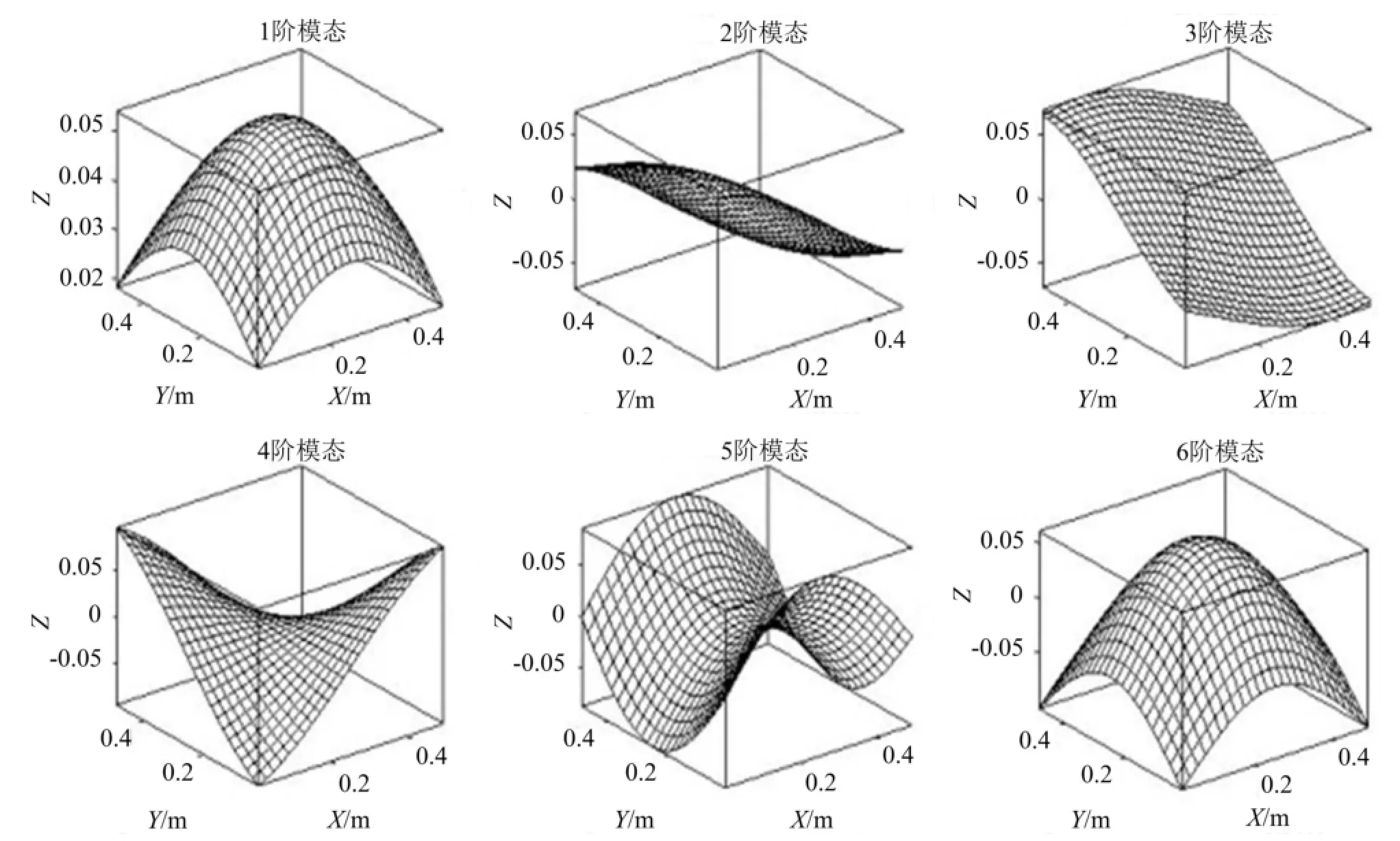
图1 平板前6阶声压声辐射模态
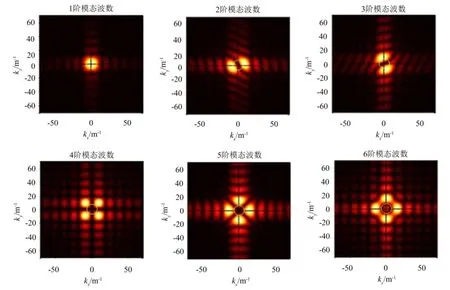
图2 平板前6阶声压声辐射模态对应波数域谱
2 误差传感策略
根据式(2)可知,基于声压声辐射模态的有源控制策略就是要通过控制使前K阶声压声辐射模态辐射的声功率最小化,即ci→0,i=1,2,…,K。那么,与之相对应的误差传感策略应能够提供前几阶声压声辐射模态的伴随系数信息。分析式(1),可以发现利用结构表面声压分布求解模态伴随系数需首先解决两个问题:(1)实际应用中只能测量近场声压;(2)实际应用中很难获得结构表面所有的声压分布。文献[9]对问题(1)进行了研究,并得到结论:只要测量面与源面间距远小于声波波长,则与源面等面积的测量面声压可以近似作为有源控制的误差变量。基于此,针对问题(2)具体设计一种少测点条件下基于声压声辐射模态的近场声压误差传感方法,来获取前几阶声压声辐射模态伴随系数的近似值。
由声压声辐射模态的空间滤波特性可知,式(1)的右端具有良好的收敛性。为简化计算,可采用模态截断的形式来表示(考虑频率相关项ω),

其中M为模态截断阶数,M<<N;S为测量面面积,与源面面积相等。为了获得前K阶声压声辐射模态的伴随系数ci(i=1,2,…,K,K<M ),我们在近场测量面上选取N1个测点xl,l=1,2,…,N1,在每一个测量点xl测量近场声压,记为Pl(xl,ω )。声压向量中有N1个元素是已知的,将式(3)中包含这些元素的方程都抽取出来重新组成一组方程组,用矩阵和向量形式表示为

式中P'为N1个测点的声压值Pl(xl,ω)组成的向量;φi'为声压声辐射模态向量φi中对应N1个测点所在单元的元素组成的向量;Φ'为M个向量φi'组成的矩阵,需要注意的是,这里不同向量φi'之间不再正交。
为实现少测点的目标,同时也为了保证误差传感的实时性,一般取N1<M。这时,方程组(4)为欠定方程组,将存在无数组解,常规方法无法求得准确解,采用最小模最小二乘法求解方程组(4)的最佳逼近解,也称最小模最小二乘解

3 误差传感策略对控制效果的影响
上一节中给出了基于声压声辐射模态的近场声压误差传感策略,利用近场测量面少数点的声压分布即可得到前K阶声压声辐射模态伴随系数的近似值。下面以声功率降低量作为评价控制效果的指标,分析上述误差传感策略对控制效果的影响,从而验证其可行性。
当模态截断阶数为M时,振动结构辐射声功率可由式(2)改写为
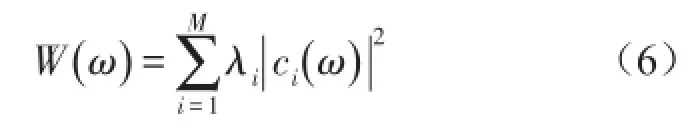
基于声压声辐射模态的有源控制策略就是要通过控制使前几阶声压声辐射模态伴随系数变为零,即ci→0,i=1,2,3,4…。那么,控制后结构的声功率为
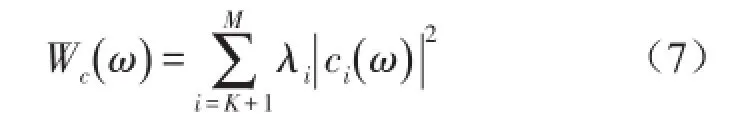
声功率降低量为

然而,当利用近似值cˆi来代替ci时,控制目标变为使cˆi→0,i=1,2,…,K,其控制后的声功率为
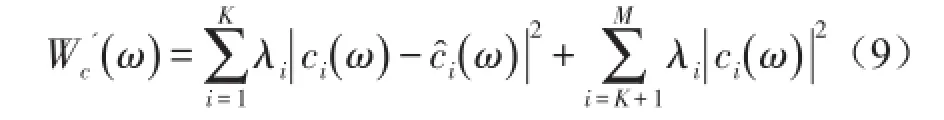
这时,声功率降低量为
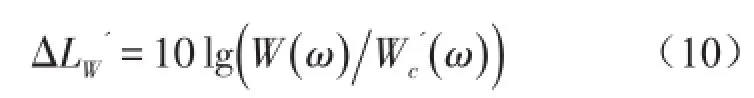
比较ΔLW和ΔLW',若两者一致,就可以判定上述基于声压声辐射模态的近场声压误差传感方法是可行的,可以作为基于声压声辐射模态的ASAC系统中的误差传感策略。
4 数值仿真分析
以置于无限大障板上的钢质简支薄板为数值研究对象。以平板左下角顶点为坐标原点,建立正交坐标系。平板尺寸为L×B×h=0.5 m×0.5 m×0.008 m,弹性模量E=2×1011Pa,泊松比υ=0.28,材料密度 ρs=7 800 kg/m3,空气中声速 c0=343m/s。在平板上位置(0.125 m,0.125 m)处施加幅值为10 N的初始简谐力Fp激励平板产生声场,频率 f取100 Hz~800 Hz。
下面通过数值仿真验证上述误差传感策略的有效性。将平板均匀离散为25×25个小面积单元,取测量面距离平板0.1 m,分别在测量面上均匀对称地取3×3和5×5个测点,其位置分布如图3所示。
利用上述误差传感策略,取模态截断阶数M=50,求解前K=4阶声压声辐射模态伴随系数的近似值。根据式(1)得到前4阶伴随系数的理论值,将近似值与之进行比较,并进行无量纲化处理,结果如图4、图5所示。

图3 测量面上测点位置分布
从图4、图5中可以看出,由式(5)得到的前4阶声压声辐射模态伴随系数的近似值与由式(1)得到的前4阶伴随系数的理论值大致吻合,尤其是第1、2、4阶几乎相等。增加测点数目,近似值与理论值更加接近。因此,利用该误差传感策略得到的声压声辐射模态伴随系数的近似值可以较好的替代理论值作为有源控制策略对应的误差信号,也即文中提出的少测点条件下的近场声压误差传感策略是有效的。

图4 测点数N1=3×3时前4阶模态伴随系数对比
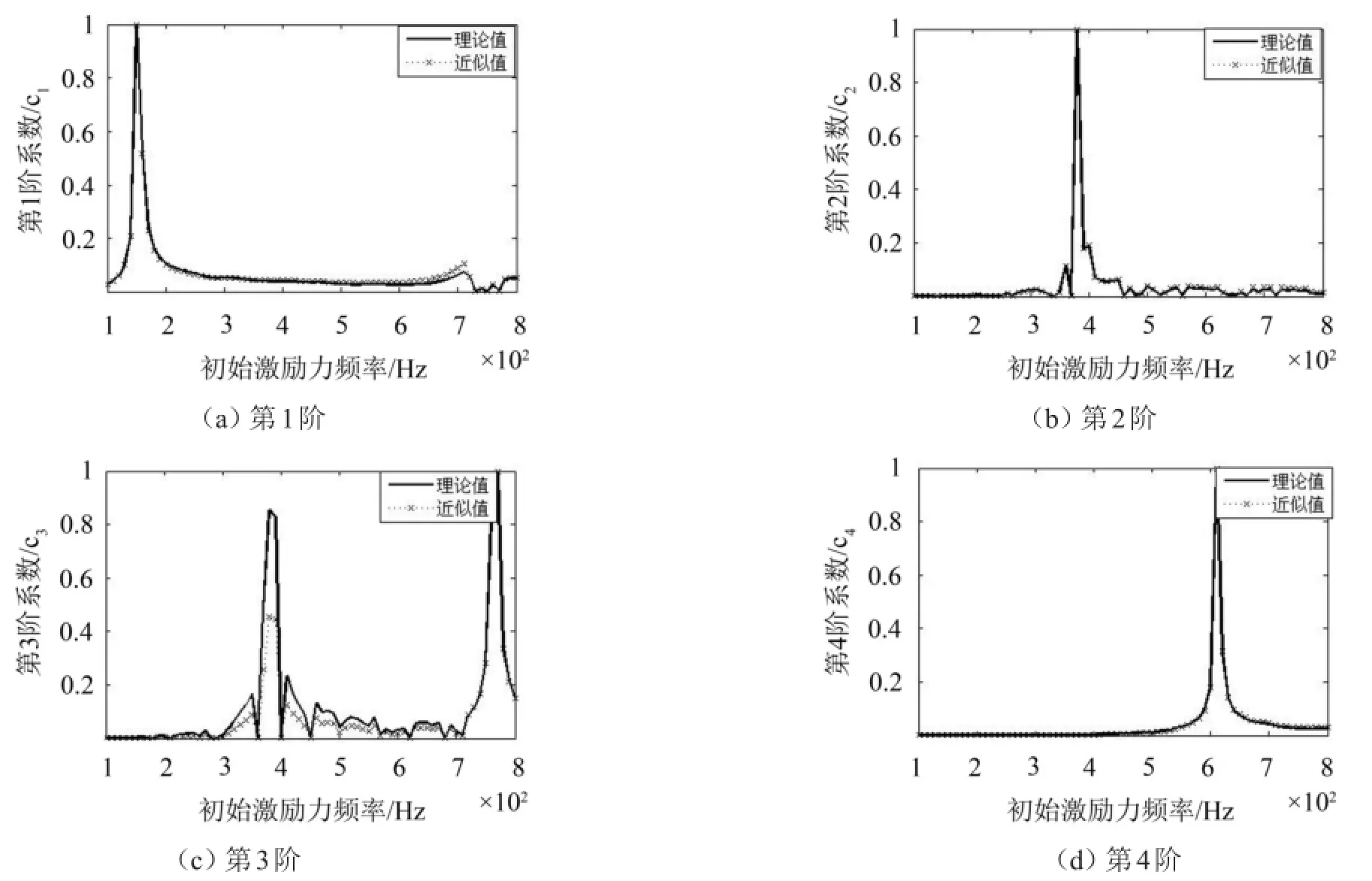
图5 测点数N1=5×5时前4阶模态伴随系数对比
另外,图中第1、2、4阶伴随系数分别在150 Hz、380 Hz、600 Hz处出现峰值,又经计算可知,150 Hz、380 Hz、600 Hz分别为平板(1,1)阶、(1,2)阶、(2,2)阶振动模态频率,分析可以发现,平板以(1,1)阶振动模态振动时,其对应的主导辐射模态是第1阶;平板以(1,2)阶振动模态振动时,其对应的主导辐射模态是第2阶;平板以(2,2)阶振动模态振动时,其对应的主导辐射模态是第4阶。这一结论和李双在文献[10]中提出的结构振动模态和声辐射模态的对应关系相符。
同时,验证将上述误差传感策略用于基于声压声辐射模态的有源结构声控制时的可行性。基于式(5)设计的近场声压误差传感策略对有源控制效果的影响,可通过对比由式(8)和式(10)得到的声功率降低量来衡量,如图6所示,实线表示根据式(8)得到的声功率降低量,即理论值;虚线表示根据式(10)得到的声功率降低量,即近似值。从图6中可知,当测点数N1=3×3时,基于式(5)设计的误差传感策略可以得到较好的控制效果,除300 Hz~570 Hz频段内存在偏差外,其它频率处与理想的控制效果基本一致;增加测点数至N1=5×5时,近似值与理论值吻合更好。这也就证明了利用式(5)得到前K阶声压声辐射模态伴随系数近似值的方法,作为基于声压声辐射模态的ASAC系统中的误差传感策略是可行的。

图6 测点数N1分别为3×3、5×5时声功率降低量比较
5 结语
针对基于声压声辐射模态的有源控制策略,具体设计一种少测点条件下的近场声压误差传感策略,即中、低频时,利用近场测量面上少数点的声压分布,通过式(5)求解前几阶声压声辐射模态伴随系数的近似值,将其作为误差传感信号实现有源控制,并以置于无限大障板上的钢质简支薄板为对象,进行了数值仿真分析。结果表明,利用上述误差传感策略获得的前K阶声压声辐射模态伴随系数具有较高的精度,且将其用于基于声压声辐射模态的有源结构声控制是可行的。
文中设计的少测点条件下近场声压误差传感策略既不受振动结构边界条件的限制,也弥补了结构表面误差传感方法在对安装传感器比较敏感的振动结构上无法有效实施的缺陷。该策略只需要测量近场少数点的声压分布,简洁,有效,易于工程实现。相比于远场声压传感,它能够实现全局控制效果,同时也使得ASAC系统简单、轻便,符合向集成式系统发展的趋势。
[1]吴锦武,姜哲.基于声辐射模态有源控制的误差传感器设计方法[J].机械工程学报,2008,44(3):189-194.
[2]聂永发.声辐射模态理论及其应用研究[D].武汉:海军工程大学,2014.
[3]TANAKA N,SNYDER S D,HANSEN C H.Distributed parametermodalfilteringusingsmartsensors[J]. Transactions of ASME Journal of Vibration and Acoustic,1996,ll8:630-640.
[4]吴锦武,姜哲.通过PVDF传感器测量振动板结构的声辐射模态伴随系数[J].振动与冲击,2005,24(4):59-61.
[5]李双,陈克安.PVDF声辐射模态传感器设计中的关键问题研究[J].西北工业大学学报,2007,25(2):295-300.
[6]吴锦武,姜哲.基于有限点振速分布设计误差传感策略[J].振动与冲击,2007,26(1):87-90.
[7]CHEN KE-AN,YIN XUE-FEI.Active control of radiated soundusingnearfieldpressuresensing[J].Chinese Journal ofAcoustics,2004,23(3):193-203.
[8] BERKHOFF A P.Sensor scheme design for active structural acoustic control[J].J.Acoust.Soc.Am.,2000,108(3):1037-1046.
[9]陈克安.自适应声学结构声压误差传感策略[J].振动工程学报,2004,17(3):301-305.
[10]LI SHUANG,CHEN KE-AN.The relationship between acoustic modes and structural modes and its applications[J].Chinese Journal ofAcoustics,2007,26(2):158-167.
Near Field Pressure Error Sensing Strategy under Less Measurement Point Condition forASAC Systems
SU Chang-wei1,2,ZHU Hai-chao1,2,MAO Rong-fu1,2,SU Jun-bo1,2
(1.Institute of Noise and Vibration,Naval University of Engineering,Wuhan 430033,China;2.National Key Laboratory on Ship Vibration and Noise,Wuhan 430033,China)
It is very important to design a simple and effective error sensing system on the basis of active control strategy.In this paper,aiming at the active control strategy based on pressure acoustic radiation modes,an equivalent nearfield pressure error sensing strategy under less measurement point condition is designed in detail.First of all,by analyzing the spatial wave-filtering characteristics of the pressure acoustic radiation modes,the feasibility of the active control strategy based on the pressure acoustic radiation modes is proved.Then,by measuring the pressure distributions at a few measurement points in the near-field measurement surface and solving the underdetermined equations made of modal superposition,the approximate adjoint coefficients of the first K order radiation modes can be obtained.Thus,a near-field pressure error sensing method corresponding to the active control strategy based on the pressure acoustic radiation modes is developed.Finally,a simply supported steel plate in an infinitely large baffle is simulated as an example.The results show that the error sensing strategy proposed is feasible and the approximate adjoint coefficients of the first K order radiation modes are more precise.
acoustics;error sensing;near-field pressure;pressure acoustic radiation mode;active structural acoustic control;less measurement point
TB535
ADOI编码:10.3969/j.issn.1006-1335.2016.04.001
1006-1355(2016)04-0001-06
2015-09-25
国家自然科学基金资助项目(51305452)
苏常伟(1990-),男,山东省滕州市人,博士生,主要研究方向为振动与噪声控制。E-mail:scwtz@163.com
朱海潮,男,博士生导师。E-mail:haiczhu@163.com

