应变模态分析及其与位移模态的关系研究

陈　晗，宋汉文

（同济大学 航空航天与力学学院，上海 200092）



应变模态分析及其与位移模态的关系研究

陈晗，宋汉文

（同济大学 航空航天与力学学院，上海 200092）

振动实验分析中，动态应变信息与位移信息具有互补性，位移响应大的地方应变响应一般较小，反之亦然。基于动态应变测量的应变模态分析理论及参数辨识与基于位移（或速度、加速度）测量的位移模态分析理论同源，但二者之间的理论关系及其相互修正方法缺乏深入有效的研究。以等截面直梁为对象，首先导出激励力-动态应变响应的频率响应函数表达式，讨论应变模态参数的辨识方法。在此基础上，进一步构建属于同一特征值的应变振型与位移振型之间的变换关系，并详细分析应变-位移变换矩阵的特性。仿真算例表明所建立变换关系的合理性与正确性。

振动与波；应变模态分析；频响函数；模态参数辨识

上世纪90年代初，李德葆等从原理和方法上系统地总结了实验应变模态分析，给出了推导公式、应变传递函数矩阵及测量方法和模态参数测量方法，并且只用应变测量得到了位移模态［1］。接着，李德葆等通过应变模态分析建立了振动应变响应预测的模态模型，使结构的动应力响应计算更为准确［2，3］。之后，人们大量运用应变模态理论做损伤识别和故障诊断，但对应变模态理论的进一步研究几乎没有。国外，Ewins等则着眼于先进的应变测量技术［4-7］。还有一些文献虽然探讨了应变模态和位移模态的关系，但并未详细讨论应变和位移的变换关系矩阵，也未探究应变模态数据应用于位移振型细化和修正的方法［8-10］。本文在前人的基础上，重新构建了应变模态理论，建立了应变位移的变换关系并详细分析了应变位移变换矩阵的特性，并提及了模态振型细化的过程。

1　基于应变的模态分析理论的构建

我国的模态分析技术发轫于20世纪60年代，80年代开始应变模态的研究，现在在理论和实践方面均取得一定进展。

李德葆等在文献［11］中认为应变模态和位移模态相互对应，是同一个平衡状态的两种不同表现形式，给出了几种应变响应模态模型的推导方法。基于位移的振动方程为

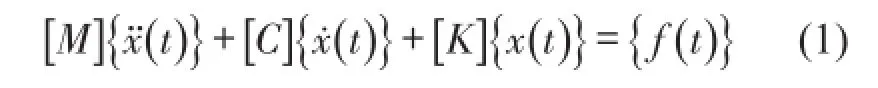
其中｛f（ t）｝是外激励，无论是简谐激励、脉冲激励还是随机激励，都可直接施加并可测。

因为模态理论是一个在线性范围内适用的理论，所以文中假设应变和位移有如下线性变换关系

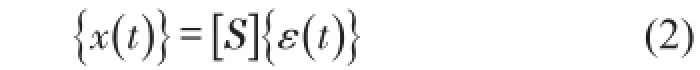
将式（2）代入式（1），左乘［S］T，并整理得

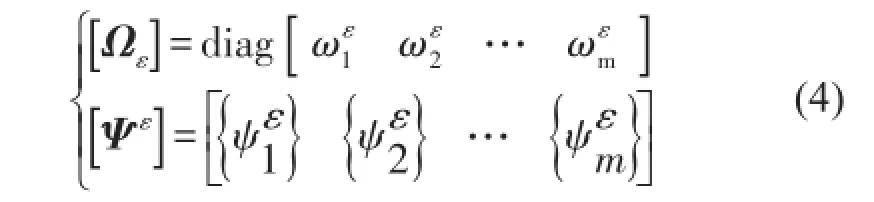
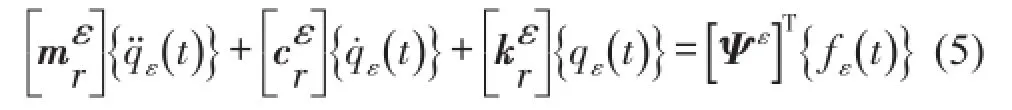
令

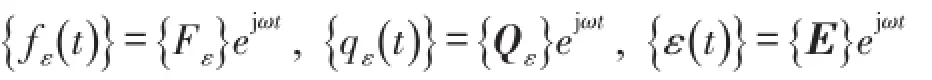
可得

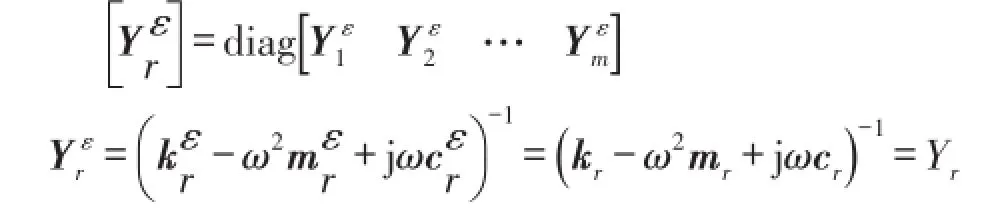
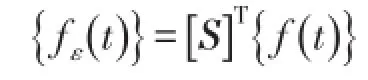
由位移模态理论易知

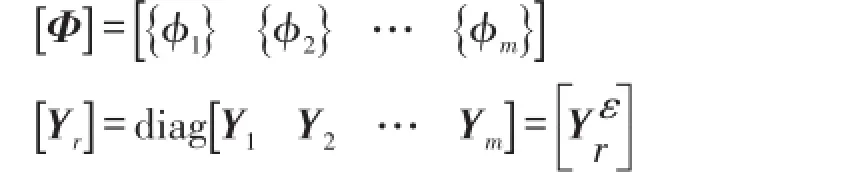
得出能用SIMO方式分析并可测的应变频响函数矩阵（SFRF）为

这个应变频响函数矩阵［Hε］不对称，若只在j点激励测i点响应，则应变频响函数为

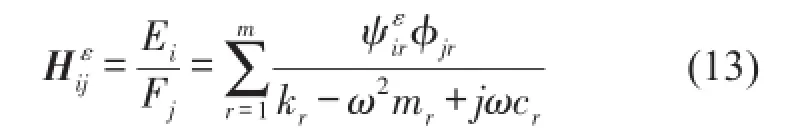
则［Hε］的第j列为

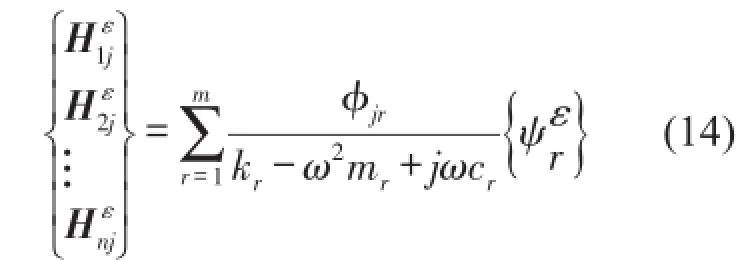
［Hε］的第i行为

测第i点激遍所有点即可得到这一行。这样就可以得到位移模态振型｛ϕr｝。像分析位移模态一样对这些应变频响函数曲线进行模态分析便能得到相应的模态参数（固有频率、阻尼比等）。

但是在实际测量中，激遍所有点比较麻烦，所以采用加速度传感器和应变片对位布置的测量方法，这样只需激励1点测遍所有点就可以同时得到位移模态和应变模态。因此，由文献［11］整理可得进行应变模态试验分析的较优方法是：

（1）在一个选好的t点激振，结构其余点无激励力输入，而在结构的各点用加速度传感器测得加速度响应，得到加速度频响矩阵［H］的一列，然后用成熟的位移模态参数识别方法得到 kr、mr、cr及｛ϕr｝；

（2）在t点激振后可用与加速度传感器对位布置的应变片同时测得结构各点的应变响应，得到［Hε］的一列的n条应变频响函数曲线（ω）（i=1，2，...，n）；

（3）考虑为实模态情况，采用下式作为曲线拟合的依据

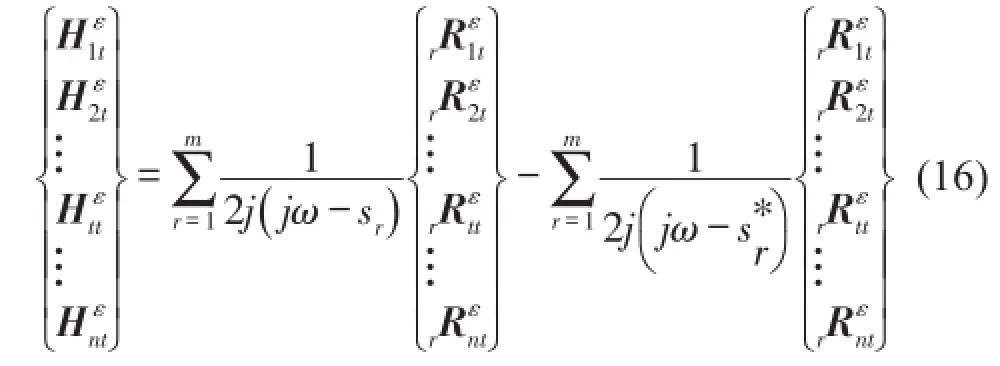
mr、νr和ϕtr已由位移模态分析中得到。

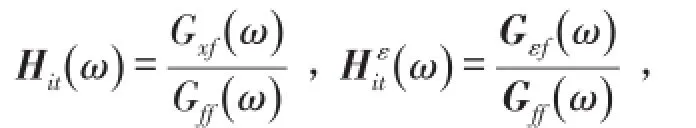
2　应变和位移关系的建立

从上述应变模态理论和应变模态试验分析可知：建立具体的n测点应变数据和n测点位移数据之间的关系是理论成立的关键。

已知需要建立的关系式为：［Φ］=［S］［Ψε］，［S］矩阵为满秩常矩阵，维数为n×n，因此有n×n个未知量，n为测点数；［Ψε］和［Φ］矩阵可以通过上节的应变模态试验分析方法求得，维数为n×m，m为模态阶数。在工程实际中，模态分析一般是多测点、少模态，即布置成百上千的测点去分析结构振动的前几阶或十几阶模态。这是因为

（1）高阶模态对结构响应的贡献很小，可以忽略；

（2）如果测点布置不合理，在某阶模态之后就会出现模态分析的定性错误，再也不能得出正确的模态振型，布置再多的测点也没用。在对一个未知结构做模态测试时，并不能提前知道如何最合理地布置测点，一般等间距布置或根据工程经验，这就导致布置n个测点并不能得出正确的n阶模态振型。

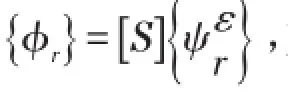
但实际结构往往比较复杂（复杂的连接方式、组成材料的复杂、局部自由度等），有限元建模不够准确，以致应变和位移的关系难以准确建立，导致具体应用时具有局限性。所以，先讨论较简单的梁结构模型，见图1。

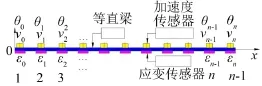
图1　等直梁模型示意图

设如上等截面直梁只做横向弯曲振动，并沿梁长方向建立坐标系，布置n+1个测点，根据文献［7］则有

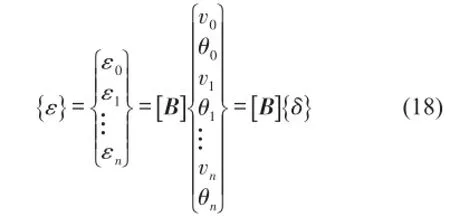
为测点位移列向量。式（18）可进一步写为

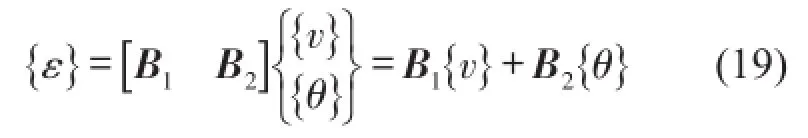
其中

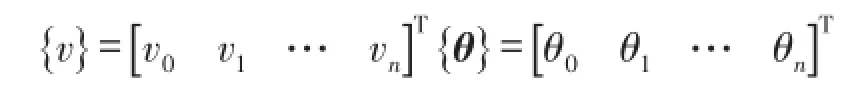
B1和B2为［B］的分块矩阵

在模态坐标下则有

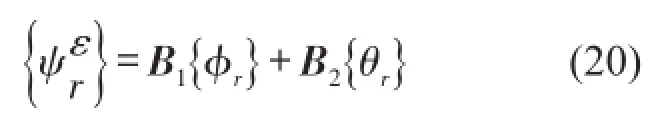
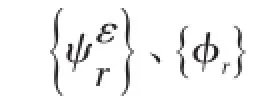
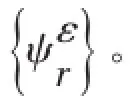
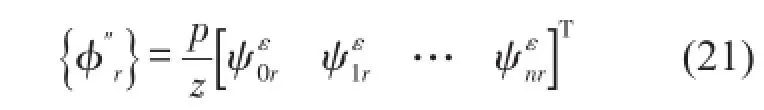
对客户而言，这个行业没有最好的月嫂，也没有最贵的月嫂，只有合适的月嫂。并且，标准不能取代服务，标准的机械化可能还会影响服务效果。母婴服务就是要形成人性化的服务，母婴服务的核心竞争力就是人性化，要逐渐地让母婴服务变为价值性、稀缺性、不可替代性、难以模仿的服务。那在母婴服务中如何体现核心竞争力呢？这就要求我们的母婴护理师具备以下四个要素：职业忠诚度、职业适应力、沟通能力和法律素养，要让母婴服务变成有感情的服务。

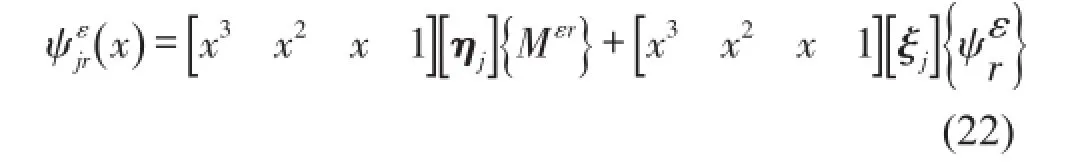
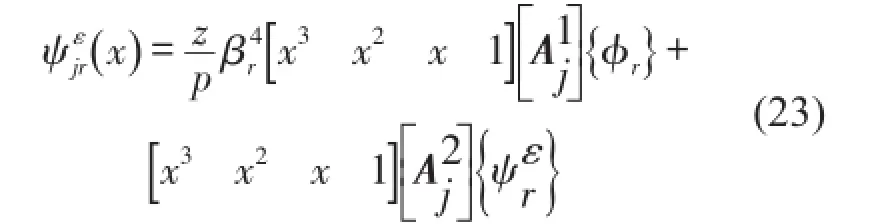
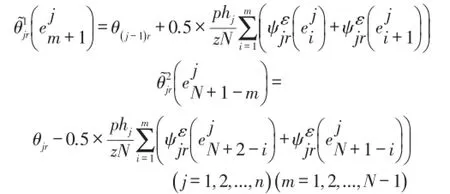
转角的计算值取

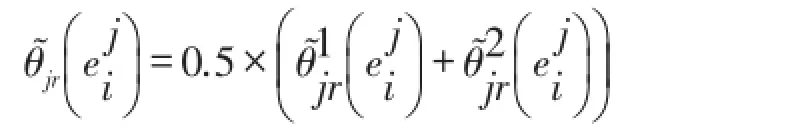
在非测点处认为

在测点处认为

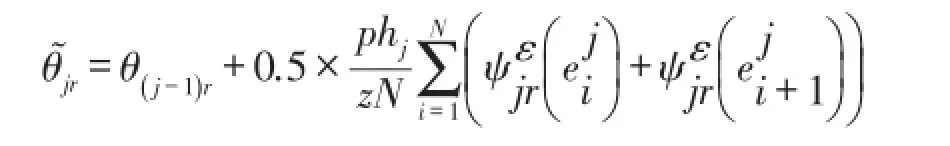
则有下列矩阵表达式

数值积分第二次可得

由式（26）进一步推得

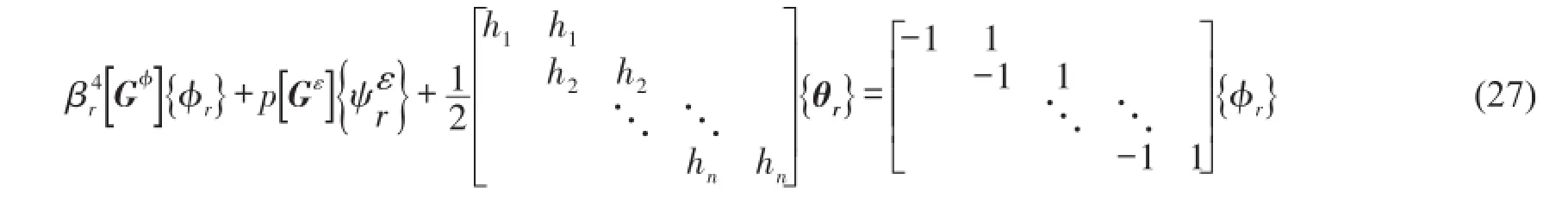
以悬臂梁为例，有约束ϕ0r=0，ψεnr=0，θ0r=0（其它约束情况以此类推），则可得

进一步记为

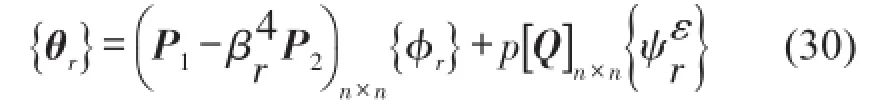
这就得出了位移、转角和应变模态振型之间的关系。［P1］、［P2］和［Q］都只与测点坐标值有关，为常矩阵。易知，如果位移、转角和应变模态振型之间是相互对应的，即满足下面关系

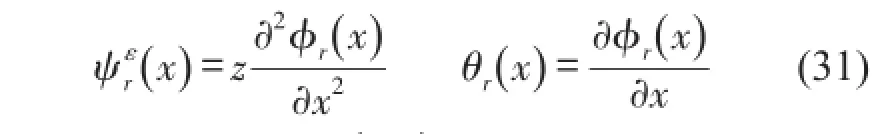
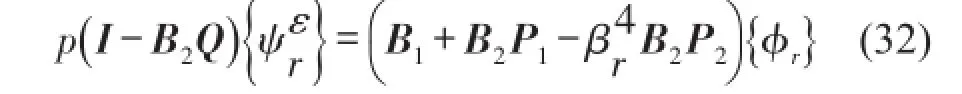
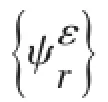
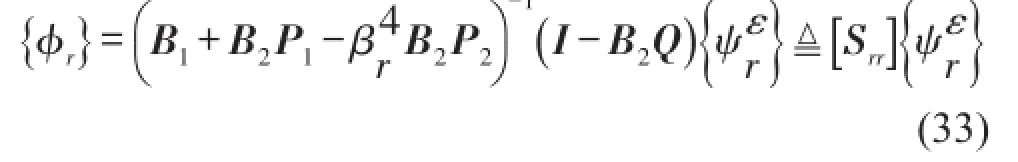
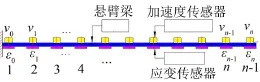
图2　悬臂梁模型示意图

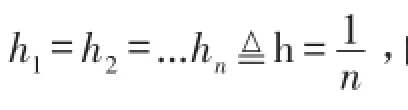
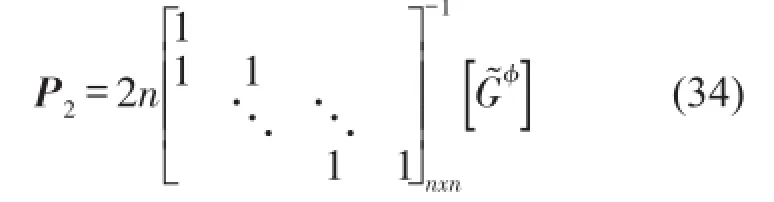
记U-1=L，则

推出：

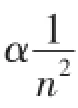
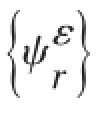
3　算例和仿真

3.1关系矩阵［Sπ］的准确性

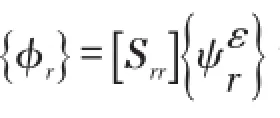
表1　计算位移振型和理论位移振型误差值

图3　前4阶计算位移振型和理论位移振型

（1）［Sπ］间的偏差

易知模态阶数相差越大，［Sπ］间的偏差也越大，故前10阶［Sπ］间的最大偏差［S10，10］与 ［ S11］的差σ=norm（［S10，10］-［S11］）随测点数n的变化关系见图4。

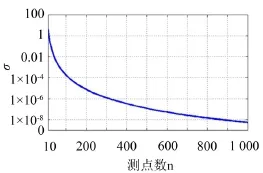
图4　偏差σ变化趋势图

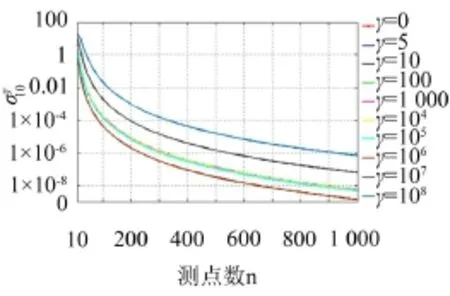
图6　偏差变化趋势图

4　结语

［1］李德葆，诸葛鸿程，王波.实验应变模态分析原理和方法［J］.清华大学学报（自然科学版），1990（2）：105-112.

［2］李德葆.结构动力分析的应变模态法［J］.机械强度，1990（3）：56-61.

［3］李德葆，张元润，罗京.动态应变/应力场分析的模态法［J］.振动与冲击，1992，12（4）：15-22.

［4］MILENA MARTARELLI，DAVID J EWINS.Continuous scanning laser Doppler vibrometry and speckle noise occurrence［J］.MechanicalSystemsandSignal Processing，2006，（20）:2277-2289.

［5］MAIO D DI，EWINS D J.Continuous Scan，a method for performing modal testing using meaningful measurement parameters；PartI［J］.Mechanical Systems and Signal Processing，2011（25）:3027-3042.

［6］GIULIANI P，MAIO D DI，SCHWINGSHACKL C W，et al.Six degrees of freedom measurement with continuous scanninglaserdopplervibrometer［J］.Mechanical Systems and Signal Processing，2013（38）:367-383.

［7］ANTHONY B STANBRIDGE，MILENA MARTARELLI，DAVID J EWINS.Measuring strain response mode shapes with a continuous-scan LDV［EB/OL］.http://proceedings. spiedigitallibrary.org/on 02/23/2014 Terms of Use:http:// spiedl.org/terms.

［8］YAM L Y，LEUNG T P，LI D B，et al.Theoretical and experimental study of modal strain analysis［J］.Journal of Sound and Vibration，1996，191（2）:251-260.

［9］魏少东，何小斌.自由梁的位移、应变和声模态分析［A］.现代振动与噪声技术（9卷）［C］.2011：296-299.

［10］KRANJC T，SLAVIC J，MBOLTE ZAR.A comparison of strain and classic experimental modal analysis［J］.Journal ofVibrationandControl，2014，DOI:10.1177/ 1077546314533137.

［11］李德葆，陆秋海.实验模态分析及其应用［M］.北京：科学出版社，2001.

［12］F´ABIO LUIS MARQUES DOS SANTOS，BART PEETERS，HERMAN VAN DER AUWERAER，et al. Strain-based experimental modal analysis:use of mode curvature and strain-to-displacement relations［EB/OL］. 2015-3-10.http://www.researchgate.net/publication/ 278963104.

Analysis of Strain Modals and the Relationship between the Strain Modals and Displacement Modals

CHENHan，SONG Han-wen

（School ofAerospace Engineering andApplied Mechanics，Tongji University，Shanghai 200092，China）

In the vibration test analysis，there is a mutual complementarity between dynamic strain data and dynamic displacement data，i.e.strong displacement response usually corresponds to weak strain response and vice versa.Strain modal analysis theory and parameter identification based on the measurement of dynamic strain are considered to be homologous with displacement modal analysis theory based on the measurement of displacement（or velocity，or acceleration），but the relationship and mutual modification of them are lack of further study.In this paper，taking a cantilever beam model as an example，the expression of the dynamic strain frequency response function to the exciting force is derived and the strain modal parameter identification method is discussed.On this basis，the transformation relation between the displacement modal and the strain modal with the same eigenvalue is established，and the characteristics of straindisplacement transformation matrix are deeply analyzed.The numerical simulation and example show the rationality and correctness of the transformation relation.

vibration and wave；strain modal analysis；frequency response function；modal parameter identification

O32

ADOI编码：10.3969/j.issn.1006-1335.2016.04.002

1006-1355（2016）04-0007-07

2016-01-29

国家自然科学基金资助项目（11272235）

陈晗（1991-），男，湖南省人，硕士生，主要研究方向为模态分析。

宋汉文，男，教授，博士生导师。E-mail:hwsong@tongji.edu.cn