地球旋转效应对X-型内孤立波间波-波相互作用的影响❋
泮龙翔,袁春鑫
(中国海洋大学数学科学学院,山东 青岛 266100)
海洋内波是最大振幅出现在密度稳定层化的海洋内部的一种波动,频率在惯性频率和浮性频率之间,其恢复力在较高频率时主要是重力与浮力的合力(称为约化重力),在接近惯性频率的较低频率时主要是地转科氏力,故内波也称为内重力波或内惯性-重力波[1]。一个振幅高达百米量级的内波通常仅仅能在海表面引起厘米量级的海表起伏,所以内波通常不易被常规观测手段发现。内孤立波是内波中较为重要的一类,通常以强非线性为特征,在过去的几十年里得到了广泛的关注和研究[2]。
大量的研究表明,内孤立波在几个惯性周期内长距离传播时,长时间施加的地球自转的影响变得十分重要,是研究内孤立波不可忽略的一部分。最初的理论研究之一是基于水平方向一维的扩展Korteweg-de Vries(KdV)方程,即含旋转项的KdV方程,也被称为Ostrovsky方程[3],来研究旋转对内孤立波的影响。旋转效应会施加一个全局的频散作用,打破内孤立波的非线性和频散的平衡,将内孤立波分解为非线性较弱的惯性重力波,最终形成一个非线性波包,这意味着Ostrovsky方程不支持稳定的KdV孤立波解[4-5]。Grimshaw[5]通过理论分析和数值计算,Grimshaw等[6]通过实验室实验,Grimshaw等[7]通过SAR图像进一步证实了该波包的产生,而且一些理论方程的结果也验证了该波包的存在,例如,Helfrich等[8]使用的完全非线性、弱非静力近似的界面波MCC方程,Grimshaw等[9]构造的高阶非线性薛定谔方程,以及Yuan等[10]使用的强迫Ostrovsky方程。有趣的是,当一个波包追赶上另一个波包时,既可以相互穿过,也可以合并形成一个更长的波包[8]。既然Ostrovsky方程会破坏稳定的KdV孤立波解,那么Ostrovsky方程是否存在稳定的解呢?Gilman等[11]通过一个近似的渐近过程,构造了Ostrovsky方程的近似渐近解,即一个孤立波在一个弱背景长波上绝热运行,当使用变系数Ostrovsky方程时,就可以研究地球旋转和可变地形的联合效应对内孤立波的影响,其结果会导致内孤立波发生相当剧烈的变形,例如,在浅化地形和地球旋转的共同影响下,内孤立波会在通常因水深变浅产生的尾波包后面额外生成一个非线性波包[12]。
地球旋转对水平二维内孤立波影响的研究则较稀少,这其中Kadomtsev-Petviashvili(KP)方程正是描述三维空间中内孤立波的典型模型,它最初是由Kadomtsev和Petviashvili[13]推导得到,然后由Grimshaw[14]进一步将其推广使其适用于内孤立波的研究,它通常被认为是KdV方程的一个二维情况的推广,该方程使人们可以更全面多角度地去研究内孤立波,例如,蔡树群[15]使用带地转效应项、高阶非线性项、摩擦项和保证波动能量能通量守恒项的扩展KP方程研究了地转对有无真实底地形、不同振幅入射波、两个不同源地入射波在传播过程中的影响,发现由于横向扩散效应,导致波场的演化更加复杂;Yuan等[16]通过KP方程研究了二维变化地形对内孤立波传播的影响,通过方程的渐近解解释了横向的变化是如何影响内孤立波形变的。
由于海洋复杂的岸线形状和海底地形,使得不同位置产生的沿不同方向传播的内孤立波很容易以一定的倾角相互碰撞,进而发生斜向的波-波相互作用。同时,当内孤立波遇到陡峭海底地形时会发生明显的折射,有时单个内孤立波还会被切断成两个内孤立波,这样就会使得内孤立波间发生波-波相互作用的可能性大大增加。而且,这些复杂多变的斜向波-波相互作用会根据振幅和夹角的不同演变为多种波形,即使不考虑浅化地形对内孤立波振幅的放大效应,在平坦的形下理论上相互作用区域振幅最大可以达到原来的四倍[17],进而产生强剪切流,对海洋油气开采平台、输油管道、水下潜艇等设施产生严重威胁,并且引起的温跃层的起伏也会对水下通讯和军事活动产生显著影响[18]。因此,研究海洋内孤立波的斜向波-波相互作用,不仅能够加深我们对内孤立波动力学的研究,对海洋资源的开发利用和国防建设也具有重要的意义。
内孤立波间斜向波-波相互作用的研究工作最早是理论研究。Miles[17,19]最先使用KdV方程对孤立波的斜向波-波相互作用进行了研究,并发现了在相互作用区可能会出现的马赫峰。后来,Kodama[20]、Yeh等[21]将Miles理论修改并扩展其适用性到较小但有限的入射角。随着实验、观测技术和计算机的发展,Maxworthy[22]基于实验室实验,Wang等[23]基于实测的海洋数据,Xue等[24-25]基于卫星图像研究了波-波相互作用。而关于波-波相互作用的数值模拟,大多集中在KP方程上,例如,Tsuji等[26]使用带三次非线性项的扩展KP方程进行了相关研究。还有一些针对波-波相互作用多发海域的研究,例如,Chen等[27]研究了中国南海内孤立波的斜向波-波相互作用,并解释了长波峰线内孤立波在长距离传播后不会衰减的现象。Shimizu等[28]利用高分辨率三维MITgcm模型和扩展Miles理论,研究了安达曼海类孤立波间的斜向相互作用,其中还研究了马赫峰的发展及低纬度地区地球旋转的影响,这里马赫峰是波-波相互作用的一个重要结果,本文也将讨论地球旋转对其产生的影响。当斜向波-波相互作用发生时,振幅和夹角之间的关系非常重要,尤其是变化地形的加入,会使演化变得更加多样和复杂。Yuan等[29]在浅化地形下对此进行了深入研究,该研究考虑的初始波形是V-型的,据其分类,在无旋转无底地形情况下,不同振幅夹角的初始V-型波将演化为6种情形,其中有两对虽然数学表达不同,但是可以通过一个简单坐标变换后,发现是物理上等同的,故本质上只有4种情形:第1种在相互作用区出现了相移,并会演化成所谓的X-型波;第2种在相互作用区出现一个马赫峰,即X-型波中心将由点变为线段状;第3种是共振相互作用,会产生第3个分支,构成了所谓的Y-型波;而第4种结构复杂少有研究。最近海洋中常见的另外一种X-型内孤立波间的波-波相互作用也得到了研究[30]。X-型波则会演化为4种情形,除去对称的1种情形,本质上只有3种情形:第1种在相互作用区同样出现了相移;第2种在相互作用区出现了一个等腰梯形结构,梯形较短的底边便是马赫峰;第3种在相互作用区出现了更为明显的相移。在卫星图像上经常可以很容易地找到这些形状的波-波相互作用引起的相应形状的海表面起伏[25,27],这只是我们通过卫星能够观测到的一部分,可知这些形状的波-波相互作用在真实海洋中是经常发生的。
注意到上述研究中鲜有考虑地球旋转的影响,Shimizu等[28]虽然考虑了旋转的影响,但主要是以安达曼海的MITgcm数值模拟结果为主,用KP方程对数值模拟结果进行了解释,提供了很多新颖的观点。不同于Shimizu等[28]的“案例研究”,本文更像是动力学机制探讨。首先我们的实验基于Yuan等[30]用KP方程的解析解发现的呈X-型的两个初始内孤立波的除奇异点外的全部4种演变情形,并将较强的地球旋转和无旋转情形进行了对比实验,然后考虑了不同强度的地球旋转的影响,即在不同纬度,这也不同于Shimizu等[28]考虑的低纬度安达曼海。
综上所述,虽然内孤立波间的斜向波-波相互作用以及地球旋转对单个内孤立波的影响已经得到了一定程度的关注,但地球旋转对内孤立波间的斜向波-波相互作用的影响仍然不清楚,因此本文使用带旋转项的KP方程,将X-型波作为初始条件,进一步研究地球旋转对其的影响。并简要描述了KP方程、初始X-型波的表达式,以及求解KP方程的边界条件和数值方法。从已经观测得到的波-波相互作用形态中,选择了其中出现频率较高的3种进行研究,并得出演化结果。最后进行总结和讨论。
1 方程
1.1 KP方程
在旋转流体中,考虑到不同的背景环境,描述波振幅A(x,y,t)的KP方程[14]可以表示为:
(1)
式中x,y,t是水平空间和时间变量,且下标表示对对应变量进行求导运算。线性相速度c(x,y)、线性放大系数Q(x,y)、非线性系数α(x,y)、色散系数β(x,y),γ(x,y)和旋转系数υ(x,y)都可以从垂直方向z的模态方程中确定:
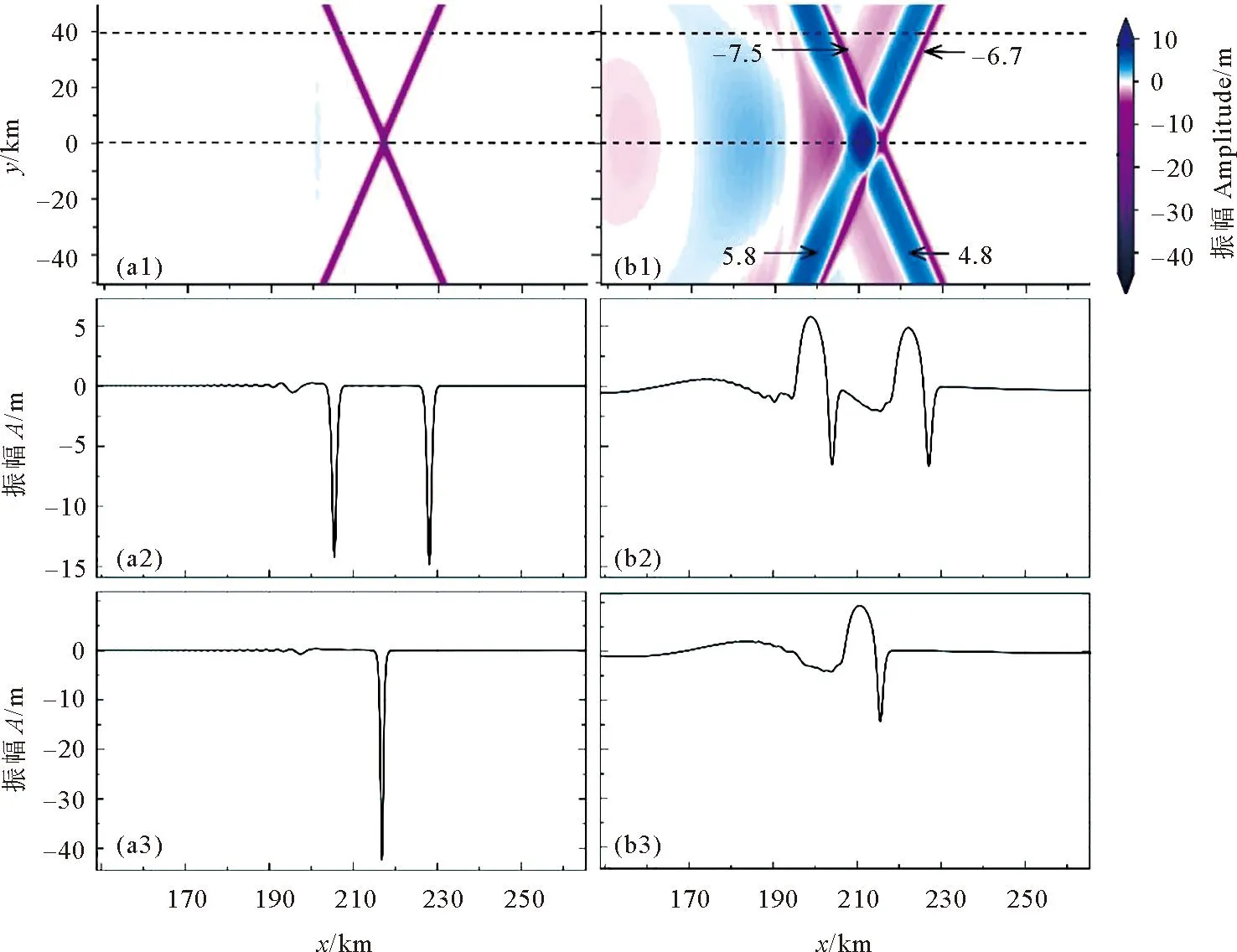
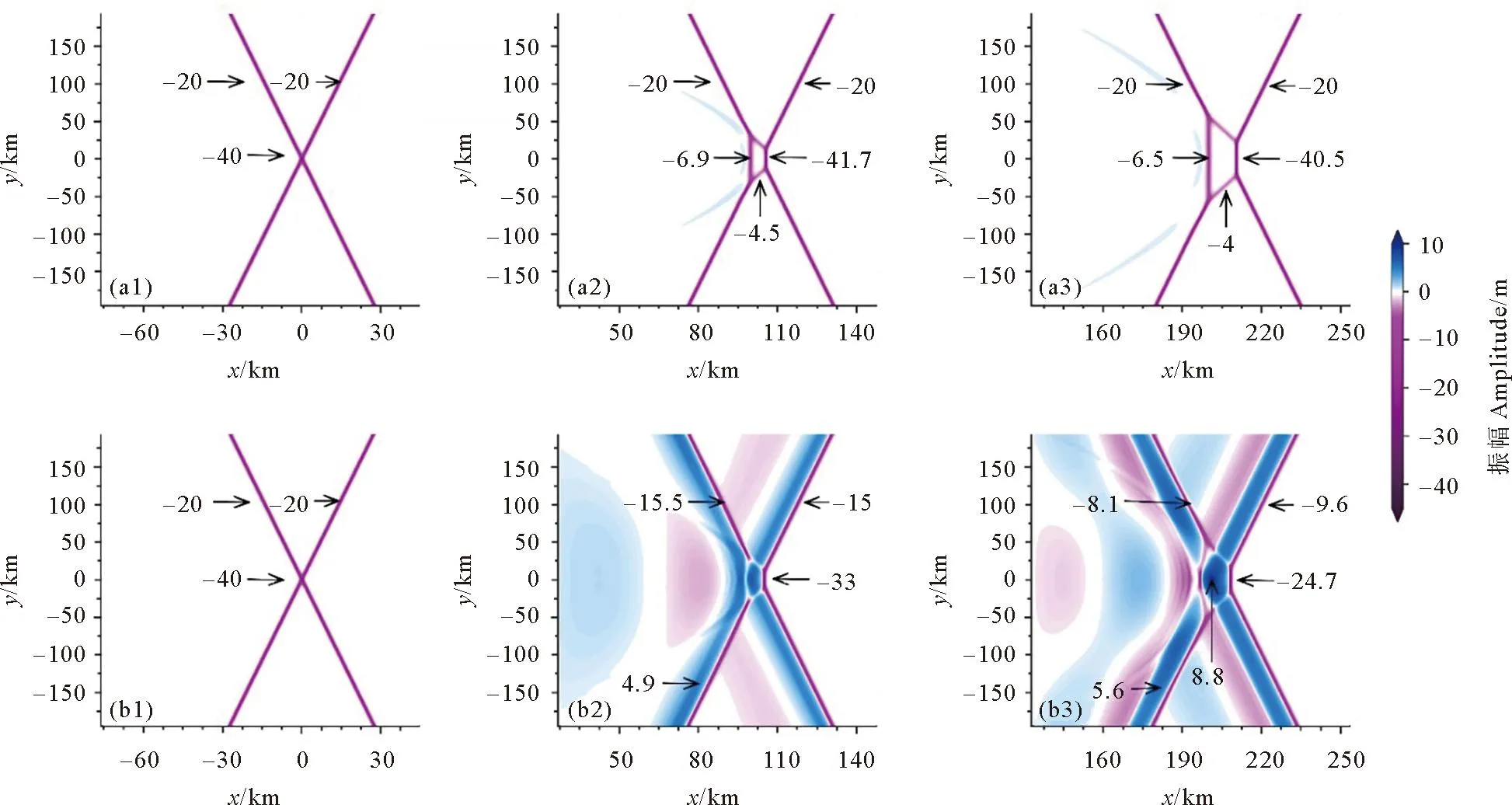
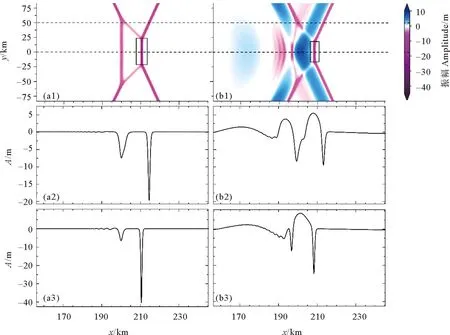
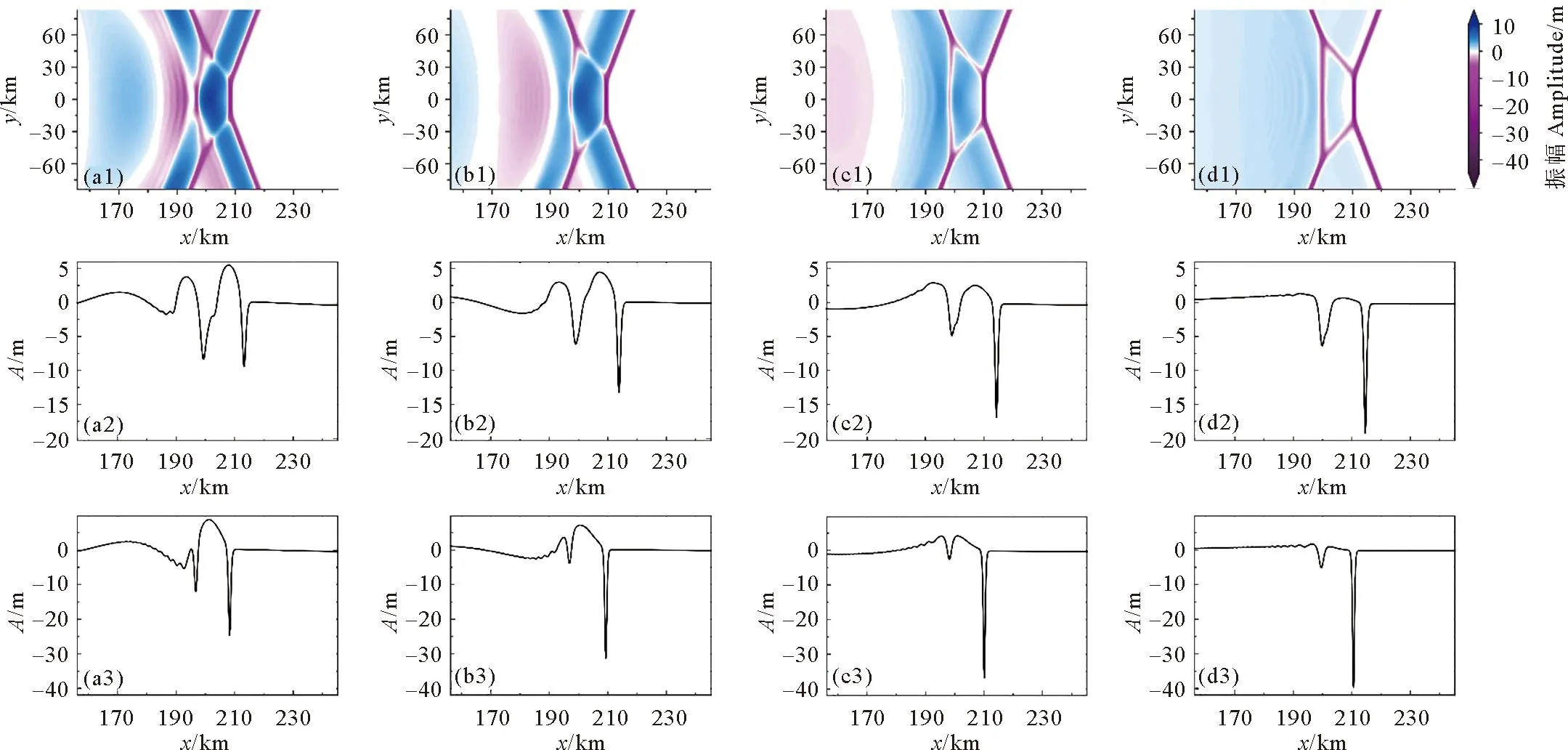
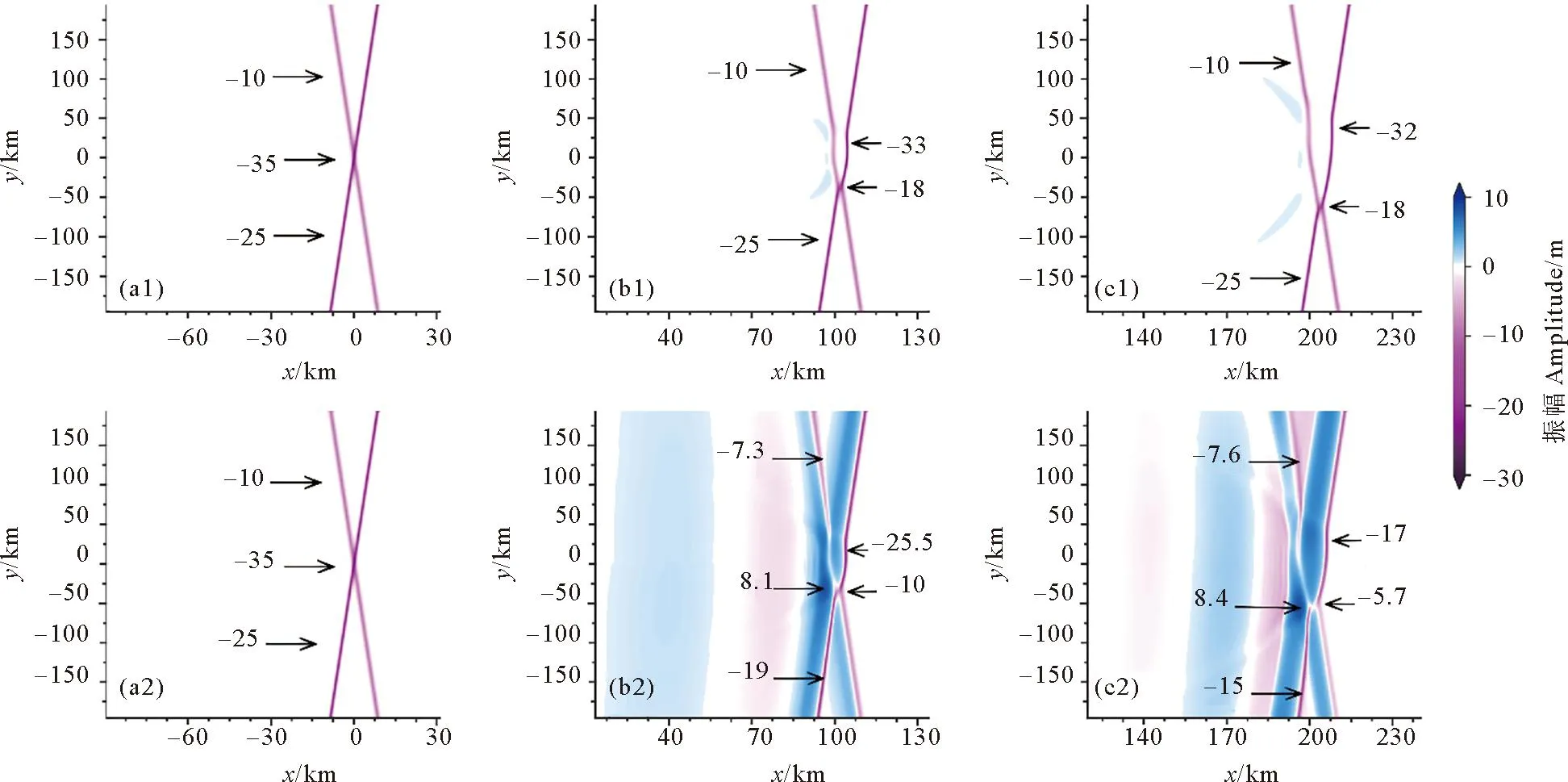
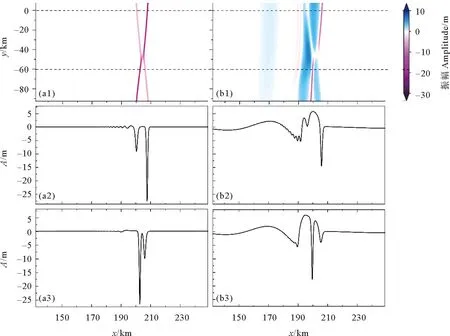
{ρ0(c-u0)2φz}z+ρ0N2φ=0,-h (2) φ=0,z=0,-h。 (3) 式中:h(x,y)是水深;ρ0(x,y,z)为背景密度分层;u0(x,y,z)为背景剪切流,密度分层通常是由浮频率N来表征的,定义为ρ0N2=-g∂zρ0。该模态方程确定了无限多个具有相应相速度cn的模态φn,n=1,2,3…,在这些模态中,我们关注模态-1(n=1)的内孤立波。方程系数的表达式可以查看文献[29,31]。 在本文中我们的分层在水平方向上是均匀的,即ρ0=ρ0(z),并且剪切情况不存在u0≡0,这使得γ=c,υ=f2/2c,其中f=2ΩsinΨ,是科氏力频率,在传统近似下,只考虑地转科氏力向量的垂向分量,其中Ω=2π/24h≈7.3×10-5s-1,是地转角速度,Ψ是纬度。使用以下变换以便数值模拟: (4) 式中x0是x方向的初始位置。然后得到了渐近等价的形式,更多细节见Yuan等[16], [Uζ+μUUX+UXXX]X+σUyy=κU, (5) (6) 式中:λ(y,T)=β/c3;μ即是方程(5)中的非线性系数;σ是色散系数;κ是旋转系数。 方程(5)中的κ代表了地球旋转效应的影响程度大小,理论上当考虑地球旋转效应时,稳定的孤立波解是不存在的。本文中我们是探索地球旋转效应对内孤立波间波-波相互作用的影响,因此构造初始的内孤立波解时,需要先忽略地球的旋转效应,即设置κ=0,而且该种设置也较为符合物理实际,因为在实际海洋中,地球旋转效应较为微弱,只有当内孤立波长时间传播时,地球旋转效应累积起来,才能对内孤立波施加较为明显的影响,目前的很多研究,例如Grimshaw等[7],Yuan等[10],Grimshaw等[12],也都采用了该种方式设置初始波形。接下来我们考虑恒定地形和水平均匀背景的情况,从而使KP方程(5)中的μ=μ0,σ=σ0是常数,即: [Uζ+μ0UUX+UXXX]X+σ0Uyy=0。 (7) 它可以进一步转化为规范形式: [4Λs+6ΛΛξ+Λξξξ]ξ+3ΛYY=0, (8) ζ=Rs,X=Lξ,y=MY,U=PΛ。 (9) 式中:R=L3/4;L2=M2=3/σ0;P=2σ0/μ0。Yuan等[29]详细描述了由多孤子解理论构造初始斜向相互作用波的过程,此处我们简要叙述要用的初始条件公式: (10) 式中:Λ0为振幅;C为相速度;波峰线有一个斜率tanψ,其中角度ψ是从Y轴逆时针测量所得,这个解描述了一个斜的孤立波。由两个斜内孤立波组成的X-型波被用作KP方程(5)的初始条件: (11) 式中U1和U2分别为两分支的振幅。 根据Yuan等[30]的分类,在无旋转无底地形情况下,不同振幅夹角的初始X-型波将演化为4种情形,而在Yuan等[29]的分类中,初始V-型波将演化为6种情形。如引言中所述,我们选择其中结构简单且在真实海洋中更常被发现记录、具有重要的研究价值的前3种情形展开进一步研究。其他情形要么与我们研究的情形对称,要么结构复杂在真实海洋中很少出现且易被复杂海洋环境影响,这里暂时不予考虑。 由于初始波填充整个横向域,本文使用窗口方法[32],将U转换为一个函数η,它在内部等于U,但在y=±Ly的边界附近迅速衰减为零,这本质上是U的分解: U=η+(1-W)U。 (12) 可见η=WU,W(y)是窗口函数,定义为 (13) 式中:n=95;a=1.02nln10。假设在y=±Ly的边界外,解可以用U0的形式来描述,即初始条件(11),但随相应的相位速度C(10)移动。 在计算中,我们使y方向的横向长度足够大,以避免数值误差,从而中心相互作用区域在计算时间内不受边值的影响,也保证了相互作用后的波没有机会重新进入该域来污染计算。然后通过转换 U=η+(1-W)U0, (14) 并代入(5)可得 [ηζ+μηηX+ηXXX]X+σηyy-κη= (15) 因为我们假设U0满足边界层中κ=0的KP方程(5),所以G1中除了最后含κ的项外均为零,而G2项是有效的。 由(15)将方程改写为如下形式: [ηζ+μηηX+ηXXX]X+σηyy-κη=R。 (16) 式中:R=G2+κ(1-W)U0;μ(y,ζ),σ(y,ζ),κ(y,ζ)定义在式(6)中。用X方向上的伪谱法求解了方程(16)。 为了避免刚性问题,使用积分因子法修改(16),以允许使用相对较大的时间步长 (17) 由X方向上的傅里叶变换 (18) 式(18)变为 (19) 在傅里叶空间中可以描述为 (20) 式中:F是傅里叶变换算子。我们用四阶中心有限差分法近似∂2y项。为了满足质量守恒定律,需对初始条件强加一个类似于Yuan等[29]中的基座。在时域中,使用了四阶龙格-库塔迭代,时间步长约为1.2 s。我们将KP理论方程进行数学离散,然后使用MATLAB软件自行编写程序,并进行计算。最后,结果在物理空间(x,y,t)中进行说明,从映射空间(X,y,ζ)通过变换(4)而来。 我们考虑的研究区域水平方向大小为x×y=[0:300]×[-400:400] km,对应的网格点数取为1 800×1 200,故而分辨率为1/6 km×2/3 km,垂向深度恒定为500 m。本文的实验沿用Yuan等[29]使用的3组初始V-型波振幅和夹角的具体数值,它们对应Yuan等[29]的分类中的前3种情形,但我们使用X-型波作为初始条件,这是因为在一种情形中调整振幅和夹角所得到的结果并无明显差异,其选取的数值本身就较为典型,能很好代表该情形。继续使用相同的振幅和夹角可以控制单一变量(初始波型),使以后的研究更易于进行对比,得到的结果更有价值。比如,对比两种不同初始波的实验1,我们发现,两者在相互作用区无论是波型还是波幅基本上是一样的。接下来我们根据有无旋转做了3组对比实验,其中考虑的地转科氏力频率f=1×10-4s-1,此外,在实验2的基础上,我们还对比了不同大小的地转科氏力f=1×10-4s-1、7.5×10-5s-1、5×10-5s-1、2.5×10-5s-1(对应的纬度Ψ=43.2°N、30.9°N、20°N、9.9°N)对波-波相互作用的影响。具体的实验配置可见表1。 表1 实验的配置Table 1 The configurations of experiments 本文使用了Yuan等[29]中使用的原始数据,即WOA13数据集的中国南海的月平均夏季背景温度和盐度数据,来确定我们的密度曲线ρ0(见图1)。因为模态-1内孤立波更常见且重要,所以我们将对其展开研究。这里波-波相互作用发生时,模态之间任何可能的能量转移被我们忽略了。图1所示的KP方程对应的模态函数φ=1处的深度表明,最初的最大质点位移发生在深度h≈190 m处,我们的初始波是一个下沉波,并且在演化过程中不会发生极性转换,由初始条件公式(10、11),初始波的示意图见图2(a1)。 图1 从左到右依次为方程(2)和(3)中的温度、盐度、密度(ρ0)、浮力频率(N)和相应的模态-1函数(φ)的垂直分布Fig.1 From left to right is the vertical distribution of temperature,salinity,density ρ0,buoyancy frequency N,and the corresponding mode-1 function φ in equations (2) and (3) (振幅由右侧colorbar表示,图中的箭头及对应数字为所指位置的振幅,单位均为m。The amplitudes are represented by the right colorbar; The arrows and corresponding numbers in the figure represent the amplitude at the indicated position,Unit: m)图2 实验1中(a1—a3)分别为t=0、16.6、33.2 h波形的演化,(b1—b3)分别为与a1—a3相同时间但带有旋转的情况(f=1×10-4 s-1)Fig.2 (a1—a3) are the evolution of wave patterns at t=0,16.6,and 33.2 h respectively,(b1—b3) are for the case with rotation (f=1×10-4 s-1) at the same time as a1-a3 respectively in experiment 1 在实验1中,初始X-型波两个分支的振幅均为A1=A2=-15 m,角度为ψ0=16°。在h=500 m的恒定深度下,随着初始X-型波沿x轴传播,除了中心点的振幅逐渐增大外,波形没有任何变化,在前导波后是由于质量守恒定律而产生的极性相反的尾波列,由于其振幅过小,在图2(a2、a3)中并不明显,但从图3(a2、a3)的剖面图中可以明显地看出。 图3 图(a1,b1)分别为f=0和f=1×10-4s-1情况下时间t= 33.2 h的振幅填色图;图(a2,a3)分别为f=0情况下沿着如(a1)图中所示虚线y=40 km和y=0 km的截面图; 图(b2,b3)分别为f=1×10-4s-1情况下沿着如(a1)图中所示虚线y=40 km和y=0 km的截面图Fig.3 Panels (a1,b1) exhibit the wave amplitudes at time t= 33.2 h under the respective rotational parameters f=0 and f=1×10-4s-1,panels (a2,a3) are the wave amplitude along the respective lines y=40 km和y=0 km as shown in panel (a1) for the case with f=0 and panels (b2,b3) are similar as panels (a2,a3),but for the case with f=1×10-4s-1 当考虑地球旋转的影响时,一个最显著的变化是初始X-型波的振幅在旋转项的色散作用下逐渐衰减,同时紧随下凹X-型波产生一个极性相反的上凸X-型波(见图2(b2、b3)),两个极性相反的X-型波交叉使重合处的振幅为0,见图3(b1)下凹X-型波左上和左下分支在y=0附近的白色部分,这两个分支显然被截断了,这导致了完整的下凹X-型波被破坏。在上凸X-型波后是一个振幅明显减小并逐渐趋于0的类惯性重力波尾波列(见图2(b3))。相互作用的中点的振幅由于波-波相互作用,本应快速变大到-44.1 m,但同时由于旋转效应而缓慢衰减,最终表现为由前者主导的先变大转为由后者主导的再变小,直到图中所示的-14.8 m(若是继续传播,还会减小,最终逐渐趋于零)。上凸X-型波振幅的最大值也在相互作用的中点处,为9.4 m(见图2(b3))。 由图3(b1)中X-型波左右两侧标记的振幅数值可以看出,无论是上凸部分还是下凹部分,以中心交点为界,后侧振幅(5.8 m、-7.5 m)都比对应的前侧振幅(4.8 m、-6.7 m)大,这是因为,如果忽略上凸和下凹X-型波交叉造成波幅抵消的影响,后侧波是中心大振幅部分的连续衰减,而前侧波不是,图3(b2)也能看出这种后侧振幅比前侧大的差异。而在无旋转情况下,前导波的后面由于质量守恒产生的极性相反的尾波列,由于相比于旋转引起的上下震荡的尾波太小而被吞没在上下起伏之中,虽然被破坏,但在沿y轴的剖面中依然可以辨别出(见图3(b2))在x=190 km或图3(b3)在x=195 km附近的不平滑小震荡。 接下来,初始波两个分支的振幅和夹角分别被设置为A1=A2=-20 m,ψ0=8°。与实验1情形相同的是演化出了极性相反的小尾波列,但是明显且本质的区别是在初始波交点中间产生了一个等腰梯形结构,见图4(a2、a3),对于该结构的详细分析可见文献[30]。 图4 实验2中(a1—a3)分别为t=0、16.6、33.2 h波形的演化,(b1—b3)分别为与a1—a3相同时间但带有旋转的情况(f=1×10-4 s-1)Fig.4 ((a1)-(a3)) are the evolution of wave patterns at t=0,16.6,and 33.2 h respectively,((b1)—(b3)) are for the case with rotation (f=1×10-4 s-1) at the same time as a1-a3 respectively in experiment 2 当考虑旋转的影响时,一个显著的变化是旋转的加入影响了马赫峰(即梯形结构右侧较短的波峰线,见图5(a1、a2)中小方框圈中的位置)的变长变高。具体来说,马赫峰的产生是下凹X-型波右上分支和左上分支之间以及右下分支和左下分支之间共振的结果,而旋转影响下生成的紧随下凹X-型波并与其交叉的上凸X-型波破坏了其结构,导致共振作用受到影响,从而减缓了马赫峰沿y方向变长,即马赫峰还会变长,但相对于无旋转情况下要短,而且旋转也抑制了马赫峰的变高,马赫峰振幅的变化与实验1相互作用中心点振幅的变化相同,先变大后变小。此外,等腰梯形结构也被上凸X-型波所破坏,具体来说,梯形结构的两个腰直接被截断了,上凸X-型波中心类似五边形的凸起将原本的梯形结构左侧较长的波峰线挤压成了三段(见图5(b1)),不过最左侧与y轴平行的一段,其振幅由于受到旋转下凹性质的调制而变大,从图5(a2、b3)中两条曲线的次极小值可以明显看出。其他细微的变化类似于实验1。 图5 图(a1,b1)分别为f=0和f=1×10-4s-1情况下时间t= 33.2 h的振幅填色图;图(a2,a3)分别为f=0情况下沿着如(a1)图中所示虚线y=50 km和y=0 km的截面图; 图(b2,b3)分别为f=1×10-4s-1情况下沿着如(a1)图中所示虚线y=50 km和y=0 km的截面图Fig.5 Panels (a1,b1) exhibit the wave amplitudes at time t= 33.2 h under the respective rotational parameters f=0 and f=1×10-4s-1,panels (a2,a3) are the wave amplitude along the respective lines y=50 km和y=0 km as shown in panel (a1) for the case with f=0 and panels (b2,b3) are similar as panels (a2—a3),but for the case with f=1×10-4s-1 此外,我们还对比了不同大小的地转科氏力f=1×10-4、7.5×10-5、5×10-5、2.5×10-5s-1对波-波相互作用的影响。我们利用奥斯特罗夫斯基数Os,即非线性系数与旋转系数的比值,来分析不同大小的地转科氏力对波演化的影响程度,根据Farmer等[33]的定义: (21) 式中:L为具有代表性的水平尺度,对上述不同的地转科压力f;Os依次为0.074、0.13、0.30、1.2,对于Os<1,地转效应占主导不可忽略,反之非线性项占主导,即f=2.5×10-5s-1时的地转效应较弱可忽略。 从图6中可以看出,当f逐渐变大时,在相同时刻,旋转对波的调制越明显,即对波幅的改变越大,表现为前导下凹X-型波振幅的减少量越大,和尾随的上凸X-型波振幅越大以及波尾的起伏越大。当f=2.5×10-5s-1很小时,旋转只是稍微抬起了前导X-型波的后部,与无旋转情况下差别很小。 (地转科氏力f从(a1)—(d1)分别为:10、7.5、5、2.5×10-5 s-1。The Coriolis forces f from (a1) to (d1) are 10,7.5,5,2.5×10-5 s-1 respectively.)图6 实验2中不同旋转参数的对比结果Fig.6 Comparison results of different rotation parameters in experiment 2 在这里,选择初始条件A1=-25 m,A2=-10 m和角度ψ0=3.67°。两个分支具有相同的倾斜角度,但初始振幅不同。在这种情况下,由图7及其中标记的振幅可以看出,交点沿y轴向下移动,而最大振幅却转移到了较大振幅分支上并向上移动,这也意味着交点不再是振幅最大的地方。从图8(a1)可以看出,X-型波交点左右两侧的V-型波有一个较为明显的错位,即交点处沿x轴变宽了,表现为较大振幅分支的右上部分和左下部分在交点处被截断了一样,这意味着此处振幅如同峡谷般小于两侧被截断部分的振幅。 图7 实验3中,(a1—a3)分别为t=0、16.6、33.2 h波形的演化;(b1—b3)分别为与(a1—a3)相同时间但带有旋转的情况(f=1×10-4 s-1)Fig.7 (a1—a3) are the evolution of wave patterns at t=0,16.6,and 33.2 h respectively,(b1—b3) are for the case with rotation (f=1×10-4 s-1) at the same time as (a1—a3) respectively in experiment 3 图8 图(a1,b1)分别为f=0和f=1×10-4s-1情况下时间t= 33.2 h的振幅填色图;图(a2,a3)分别为f=0情况下沿着如(a1)图中所示虚线y=0 km和y=-60 km的截面图; 图(b2,b3)分别为f=1×10-4s-1情况下沿着如(a1)图中所示虚线y=0 km和y=-60 km的截面图Fig.8 Panels (a1,b1) exhibit the wave amplitudes at time t= 33.2 h under the respective rotational parameters f=0 and f=1×10-4s-1,panels (a2,a3) are the wave amplitude along the respective lines y=0 km和y=-60 km as shown in panel (a1) for the case with f=0 and panels (b2,b3) are similar as panels (a2,a3),but for the case with f=1×10-4s-1 此外,由图7(a2、a3)可以看出,交点上方的波峰线出现了明显的弯曲,这是因为两个初始波分支振幅不同,交点沿y轴向下移动,而最大振幅却转移到了较大振幅分支上并向上移动,这导致振幅沿斜向的分支变化巨大,同时,由于质量守恒定律,导致X方向产生复杂的调制,进一步为了响应X方向的变化,y方向也产生复杂的调制,因为波的作用通量必须守恒。因此在图7(a2、a3)中,交点上方的波峰线出现了明显的弯曲,Yuan等[29]实验中产生的马赫峰也有一个非常特殊的弯曲结构,可参看其中的分析。 当考虑到旋转的影响时,产生的变化类似于实验1。上凸X-型波最大振幅与前导下凹X-型波的交点在同一y截面上,不过,由于下凹波最大振幅的上移,下凹波最大振幅与上凸波最大振幅不在同一y截面上(见图7(b2、b3))。整体来看,由旋转产生的上凸X-型波对初始的下凹X-型波造成了十分严重的破坏,也使得波形变得十分复杂。从图7(b3)可知,初始下凹X-型波左上侧分支直接被截断了,无旋转情况下交点处产生的错位则被向两侧挤压进一步变大,并且该处的振幅也被影响而变成了零(上凸X-型波右上和右下分支中间白色部分)。 旋转还会通过影响X-型波的振幅来影响交点的下移,由于旋转使初始的下凹X-型波产生了严重的变形,我们以X-型波交点右侧V-型波的振幅来说明,旋转效应使前导下凹X-型的两个分支之间振幅差变小,从图8标记的两条虚线我们可以得到相应分支的振幅。由图8(a2、a3)中两条曲线右侧第一个波峰可得振幅差为的17 m,同理在图8(b2、b3)中为11 m,根据文献[29],交点位移与振幅差成正比,可知交点下移距离减小,在图8(a1)中明显可以看出下分支比上分支短,而(a2)中则相反,这也意味着交点延y轴的位移在(a2)中较小。 当斜向波-波相互作用发生时,振幅和夹角之间不同的关系会使相互作用波演化为多种复杂的情形[29-30]。在已有的无旋转情形下波-波相互作用的基础上,我们进一步考虑了地球旋转的影响,使用带旋转项的KP方程来研究旋转效应对X-型内孤立波间波-波相互作用带来的影响。较强的旋转效应带来的一个显著影响是削弱前导波振幅,同时紧随前导波生成一个极性相反、大体仍呈X-型的尾波,后面跟着一个振幅明显减小并逐渐趋于零的类惯性重力波尾。旋转效应带来的另一个显著影响是其对马赫峰的长度和强度的影响,其他人的研究也证实了这一点,例如,Shimizu等[28]利用MTIgcm模式研究了安达曼海中的马赫峰的发展和低纬度旋转的影响,表明低纬度(≈9°N)条件下,地球自转对内孤立波的传播影响很小,但确实减缓了马赫峰的生长,与我们的结果一致。究其原因,就是旋转影响下生成的紧随下凹X-型波并与其交叉的上凸X-型波将其截断,破坏了前导X-型波的完整性,从而影响了共振相互作用下马赫峰的发展。此外,旋转还会影响波-波相互作用中心点处的位置,而且在无旋转情况下,前导波的后面由于质量守恒产生的极性相反的上凸尾波列,由于相比于旋转引起的上下震荡的尾波太小而被吞没在上下起伏之中,虽然被破坏,但依然可以辨别出。同时,我们还对比了不同大小科氏力频率f带来的影响,当科氏力频率f逐渐变大时,在相同时刻,旋转对波的调制越明显,对波幅的改变越大,表现为前导下凹X-型波振幅的减少量越大,和尾随的上凸X-型波振幅越大以及尾波的起伏越大。当旋转较弱时,带来的影响只是稍微抬起了前导X-型波的后部,与无旋转情况下差别很小。 本文的X-型波-波相互作用是发生在平坦海底地形之上的,然而事实上,海底地形是复杂多变的,尤其是在陆坡陆架、海底峡谷和山脊等位置,如果将变化地形这一要素也考虑进来,波-波相互作用也会变得更加复杂。同时,研究结果表明,背景剪切流对于内孤立波的演化过程有很重要地影响(例如Zhang等[35]和Min等[36]),本文中也没有对这一要素进行考虑。除此之外,该研究忽略了波-波相互作用过程中可能产生的模态转换现象,尤其是不同模态的内孤立波间的波-波相互作用是一个值得探索的科学问题,我们已经注意到了Stastna等[34]开展的相关研究。这些因素对内孤立波间波-波相互作用的影响是值得进一步研究的。1.2 初始条件
1.3 边界条件
G1(X,y,ζ)+G2(X,y,ζ),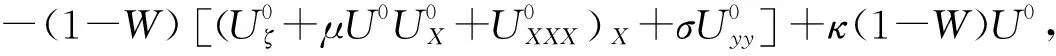
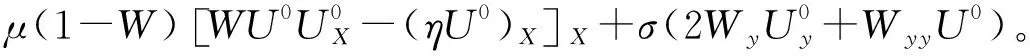
1.4 数值方法
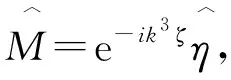
2 X-型波-波相互作用
2.1 模型设置


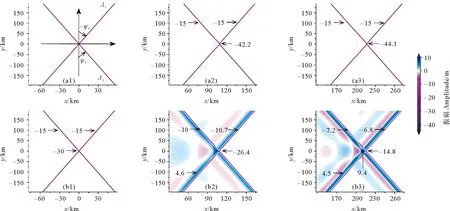
2.2 实验1
2.3 实验2
2.4 实验3
3 总结和讨论

