基于CFD方法的FPSO的波浪荷载和运动响应研究❋

左伊人,周 琦,杨风艳,张 敏❋❋

(1. 中国海洋大学工程学院,山东省海洋工程重点实验室,山东 青岛 266100;2. 浙江华东建设工程有限公司,浙江 杭州 310014; 3. 海洋石油工程(青岛)有限公司,山东 青岛 266520)

浮式生产储油船(Floating production storage and offloading,FPSO)是目前海上油气田开发生产的主流设施之一。随着海洋工程向深水推进,工程所处的海洋环境条件愈加恶劣,体现在波浪出现强烈的非线性,而波浪对其船体结构施加的荷载和造成的运动响应是工程上需要重点关注的问题。为保证FPSO在服役时的安全性和工作效率,对于其波浪荷载的计算以及运动响应的预报必须要求准确。

对于FPSO所受的波浪荷载,早期多是使用势流理论进行计算,Newman[1]提出的远场法以及Pinkster等[2]提出的近场法均得到广泛的应用,但是势流理论较难考虑流体黏性效应和强非线性效应,不能很好地反映实际工程面临的真实问题。Inoue等[3]使用近场法和远场法计算了液化天然气浮式生产储油船 (Liquefied natural gas FPSO,LNG-FPSO)系统的漂移力,同模型试验对比发现,不考虑黏性会导致漂移力的预测误差。国内的学者王科等[4]指出计算FPSO的纵摇和横摇需要考虑黏性阻尼。随着计算机技术和数值方法的快速发展,计算流体力学(Computational fluid dynamics,CFD)方法以其考虑流体黏性和非线性影响的优势开始受到广泛关注。外国学者Huijsmans[5]首次使用CFD方法计算了深水规则波作用下FPSO的二阶波浪力的传递函数。Rosetti等[6]预测了不同波陡的规则波作用下二维FPSO的波浪力,发现CFD方法可以很好地捕捉到力的最大值。Hu等[7]使用CFD求解器计算了极端波作用下FPSO的力和运动,且通过同势流结果和实验数据的对比发现,纵摇的黏性效应明显。王和静等[8]使用CFD方法计算了FPSO的平均漂移力和运动响应,发现较之势流,CFD方法会高估平均漂移力。李奇等[9]应用CFD求解器naoe-FOAM-SJTU对单点系泊的FPSO水动力性能进行数值模拟,验证了其准确性,体现出CFD进行强非线性现象仿真的优势。但是,强非线性波浪力的作用机理目前还不明晰,未提出有效的强非线性波浪荷载的预报模型[10]。

本文应用CFD软件STAR-CCM+[11]建立三维数值波浪水池,使用Richardson外推法分析了计算收敛性和数值不确定度。在数值水池中模拟了规则波作用下FPSO的垂荡与纵摇,计算迎浪波浪力,分析流场瞬时自由液面和涡量场。通过同势流结果对比,探究了黏性效应对波浪力和运动响应的影响,探究了非线性波浪力的作用机理。本文的数值模拟使用实尺度FPSO,避免船体尺度效应,充分考虑了波浪与FPSO相互作用过程中的黏性效应,对计算及修正浮体受到的二阶波浪力和运动响应具有一定的理论指导意义。

1 数值分析方法

本文以雷诺平均方程(RANS equation)为控制方程求解瞬态的黏性绕流场,采用有限体积法(Finite volume method,FVM)离散控制方程。选择欧拉多相流创建水和空气两相流体,流域为不可压缩流体,采用流体体积法(Volume of fluid,VOF)捕捉自由液面,用SSTk-ω湍流模型封闭方程,使用压力耦合方程组的半隐式方法(Semi-implicit method for pressure linked equations,SIMPLE)耦合求解速度和压力,并考虑重力的影响。对于浮体的运动,采用重叠网格技术和动态流体固体相互作用模型DFBI来模拟。

连续方程:

(1)

RANS方程:

(2)

本文采用SSTk-ω湍流模型包含的k方程和ω方程分别为

(3)

(4)

式中:k为湍动能;ω为耗散率;Γk和Γω是有效扩散项;Gk和Gω是生成项;Yk和Yω是湍动耗散项;Dω是交叉扩散项;Sk和Sω是自定义源项。

自由液面用VOF法处理,体积占比aq满足方程:

(5)

2 数值模拟

2.1 船型几何参数

本研究采用的船型为FPSO[8],采用实船尺寸以避免船舶尺度效应。计算模型参数见表1。后文中的船长均指垂线间长Lpp。

表1 计算模型参数Table 1 Parameters of the FPSO

2.2 计算域设置

本文根据文献[12]的建议对计算域进行设置:整个计算域长度约为船长的9.8倍,宽度约为船长的6.4倍;速度入口距离船首为船长的3.2倍,压力出口距离船尾为船长的6.6倍,且整个计算域包含2倍波长的消波区域;整个场域的上部为空气,下部为水,船下部边界距船体为船长的2倍。FPSO在数值水池中的设置如图1所示,因船体对称,使用FPSO一半船体进行计算。原点为O,横向(y轴)位置在中线面上,纵向(x轴)位置在船中,竖向(z轴)位置在距船舶基线18.44 m处。

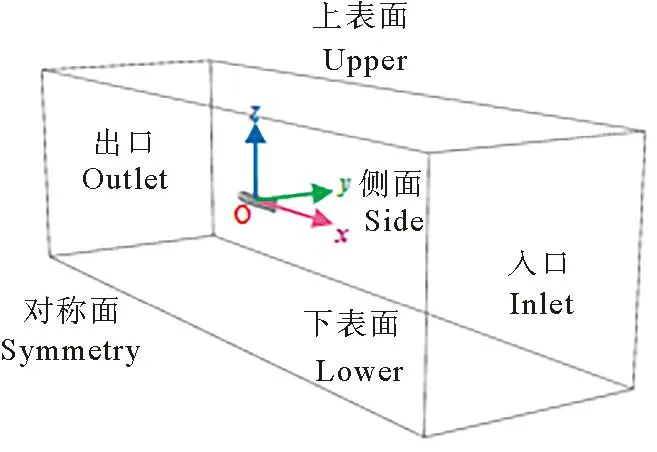
图1 数值水池示意图Fig.1 Sketch of the numerical tank

2.3 造波和消波

采用边界造波法原理,直接通过雷诺平均纳维-斯托克斯(Reynolds-averaged Navier-Stokes equations,RANS)求解器分别控制速度入口和压力出口参数来模拟造波。入口边界、侧面边界设置为速度入口,出口边界设置为压力出口,3个边界均设置强制消波[13],在消波区域强制让波浪保持入射的状态。船体表面为不可滑移固壁条件,近壁面采用壁面函数法处理。计算域顶部和底部均设置为速度入口,以更好地模拟波浪前进,减轻波浪衰减。整个流场造波效果见图2,波面高程的原点在-11.45 m。

图2 空场造波的自由液面高程图Fig. 2 Free surface elevation of wave generation

2.4 时间步长及网格尺寸收敛性验证

使用重叠网格,根据一个波高范围内划分10～20个网格,一个波长范围内划分80～120个网格的原则,网格划分如图3所示。

图3 网格划分的示意图Fig.3 Sketch of the mesh

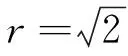
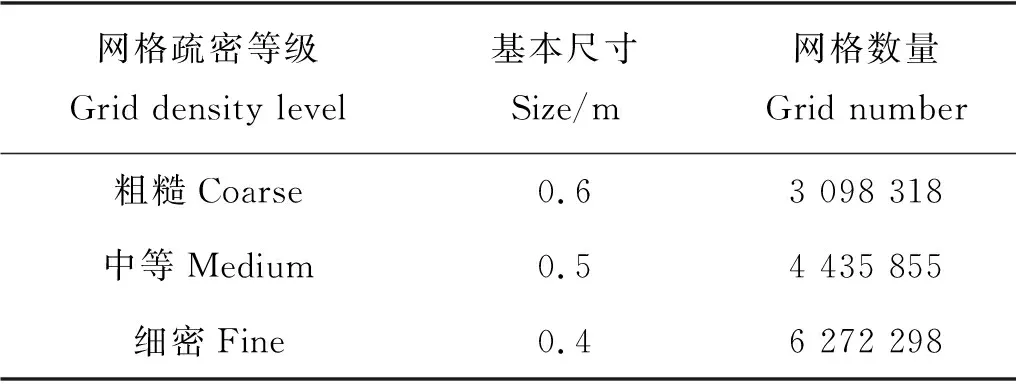
表2 网格尺寸方案Table 2 Test case of grid size

根据文献[12]的建议,设置3种时间步长,如表3所示。

首先通过空场造波验证数值波浪的可行性。3套网格下的造波结果与理论值的对比如图4所示。由图4可知,3套网格的数值结果同理论值匹配较好。

图4 不同网格尺寸条件下的造波与理论值对比Fig.4 Comparison of the numerical and theoretical free surface elevation

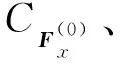
(6)

(7)

(8)

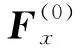
基于Richardson外推法[14-15],可以定义收敛率R、精度P、外推值Sext、相对误差估计值ea、相对误差外推值eext和网格收敛指数(Grid convergence index,GCI)I,以对时间步长和网格尺寸进行收敛性研究,并分析数值不确定度:

(9)

(10)

(11)

(12)

(13)

(14)

式中:s1、s2、s3分别为在细密网格(或最小时间步长)、中等网格(或中等时间步长)和粗糙网格(或最大时间步长)计算得到的数值结果(运动响应、力);Sext,32表示基于s3、s2的外推值;ea,32表示基于s3、s2的相对误差估计值;eext,32表示基于s3、s2的相对误差外推值。

根据收敛率R的大小,可以分成4种收敛情况:单调收敛(01);振荡发散(R<-1)。其中,单调收敛情况使用网格收敛指数表征不确定度,振荡收敛情况使用数值最大值和最小值的差值的一半来表征不确定度。表4和5分别给出了时间步长收敛性和网格收敛性的基于s2的收敛性验证结果。

表4 时间步长收敛性Table 4 Time-step convergence

根据表4可以发现,采用0.02 s的时间步长已经满足收敛。采用最小时间步长0.015 s得到的计算结果数值不确定度很低,垂荡的不确定度小于5%,纵摇和迎浪平均波浪力系数的不确定度更是小于1%。根据表5可以看出使用粗糙网格已经满足收敛。使用中等网格的垂荡和迎浪平均波浪力系数的不确定度均小于1%,且纵摇不确定度远小于1%,说明网格收敛性很好。在满足时间步长收敛和网格收敛的精度条件下,为了保证计算的物理时间效率,后续选择0.015 s作为时间步长。

表5 网格收敛性Table 5 Grid convergence

2.5 数值模型验证

使用本文的数值水池,选择和文献[8]同样的波浪条件进行计算,时历曲线对比的结果如图5所示。结果吻合良好,证明本文的数值模型具有可行性。

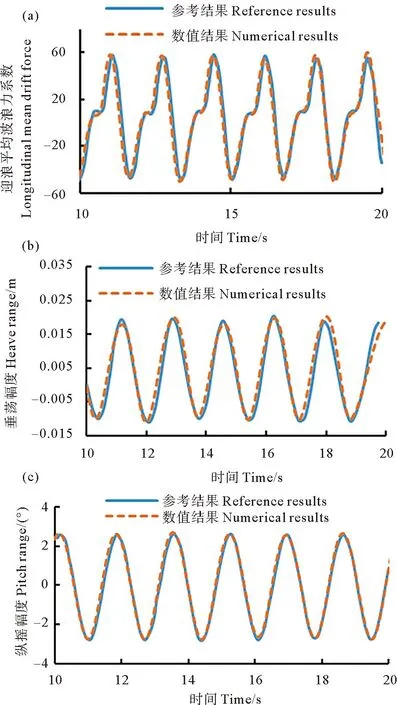
图5 数值计算结果与参考结果的对比图Fig.5 Comparison between numerical results and reference results

2.6 计算工况

为更加真实地模拟波浪,计算中使用斯托克斯五阶波 (Stokes fifth order wave)和0°浪向角(迎浪方向)。根据文献[16]中的实际海域环境条件,分别选择5组同一周期不同波高的工况和5组不同周期同一波高的工况(见表6)。由于不考虑系泊,计算过程仅开放纵摇和垂荡两个自由度。

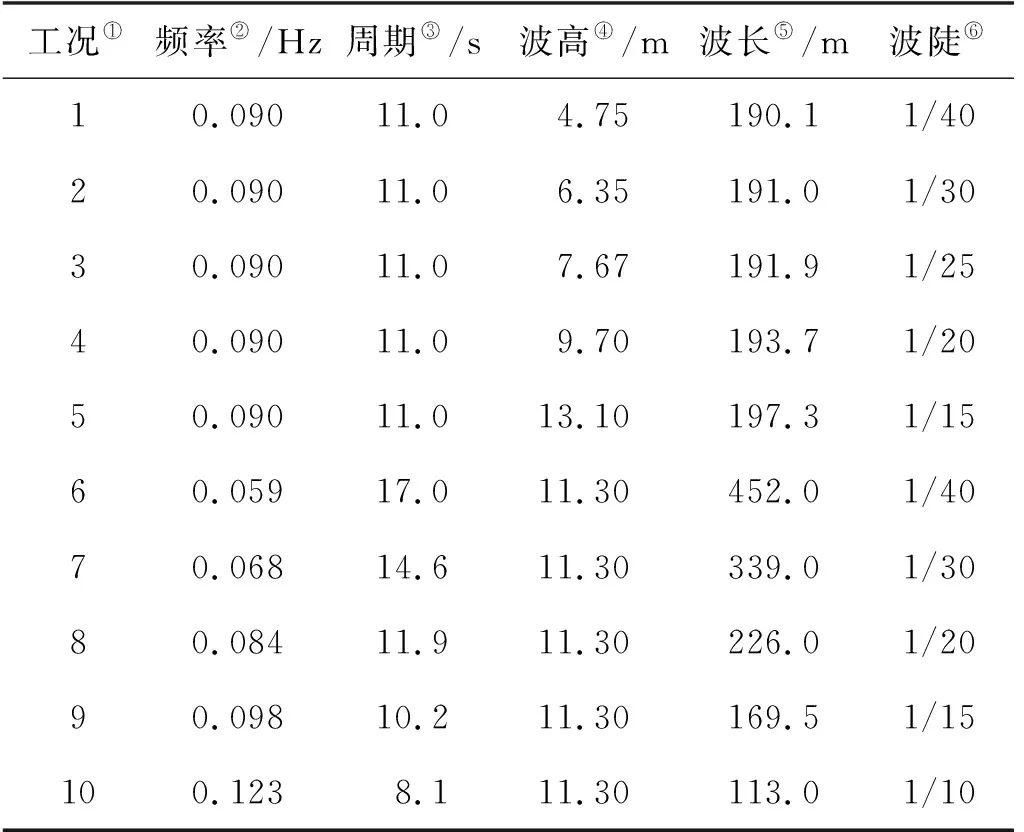
表6 计算工况Table 6 Calculation conditions

3 计算结果及分析

计算所有工况的垂荡响应、纵摇响应和迎浪波浪力。选取FPSO运动较为稳定的10个周期。

3.1 波浪荷载

图6展示了在一个波浪周期内不同波高和不同波长工况下的迎浪波浪力时历曲线。由图6(a)可知,一个波浪周期内,每种波高的工况下均存在2个极大值和2个极小值,且2个极大值的幅值较为接近,2个极小值的幅值也很接近。由图6(b)可知,在一个波浪周期内,仅在波长不大于船长的工况下可明显看到波浪力存在第二个极值。

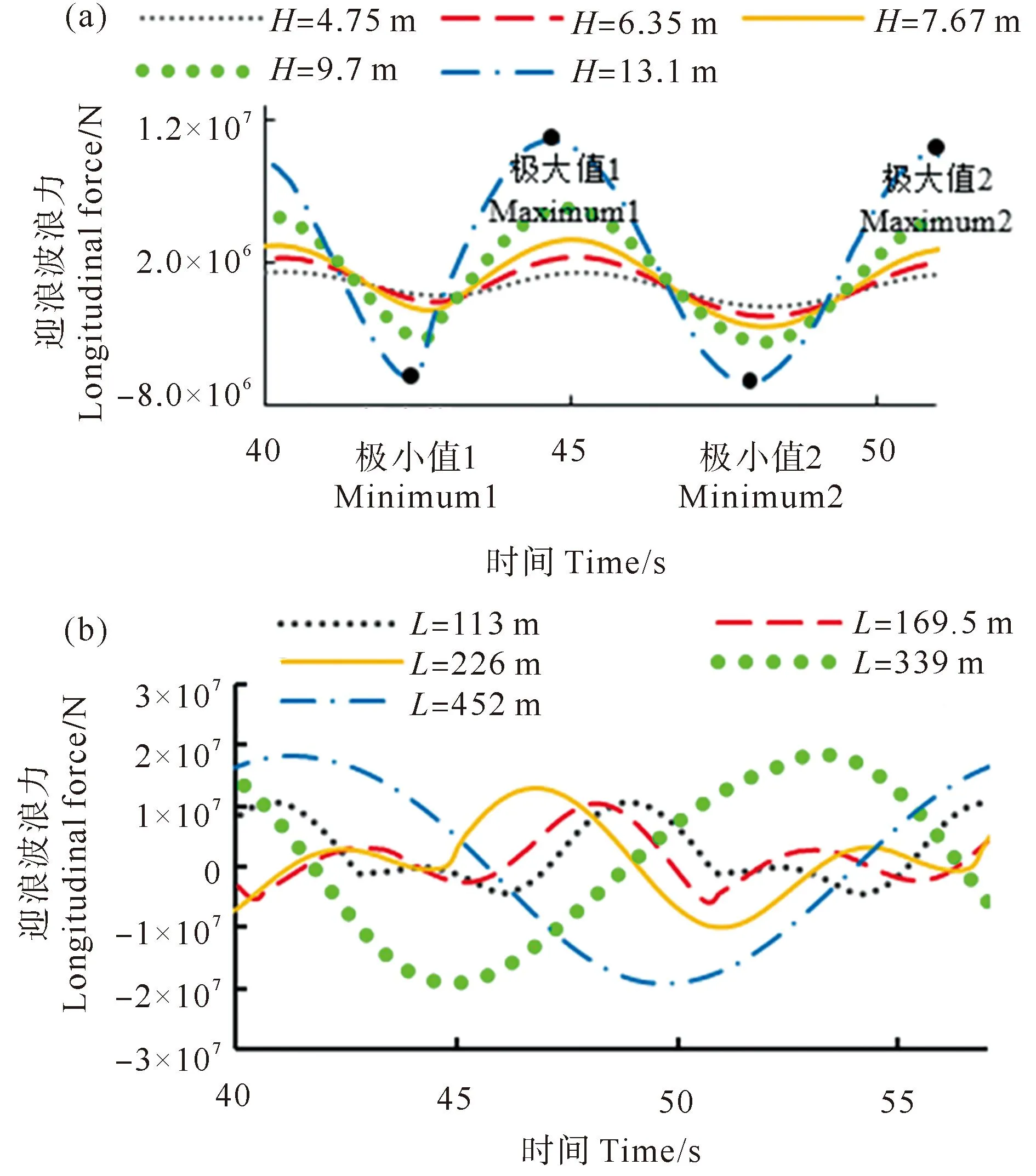
图6 一个周期内迎浪波浪力的时历曲线Fig.6 Time history of longitudinal wave forces in one wave period

对所有工况的迎浪波浪力时历曲线做频谱分析。由图7(a)可知,在不同波高的工况下,0.18 Hz(二倍波频)附近对应的力(二倍波频力)均非常大,0 Hz(0倍波频)附近对应的力(平均波浪力)也较为明显,同一波浪频率对应的力数值接近。0.27 Hz(三倍波频)附近、0.36 Hz(四倍波频)附近、0.45 Hz(五倍波频)附近均有明显数值,说明迎浪波浪力的非线性强烈。由图7(b)可知,波长大于船长的2个工况下的二倍波频对应的力非常小,其他3个工况下的二倍波频对应的力均为波频对应的力的一半以上。综合图6和7分析得知,波浪力时历曲线中,一个周期内存在2个极大值和2个极小值,且均同二倍波频有关,二倍波频对应的力越大,第二个极大值和第二个极小值越明显。

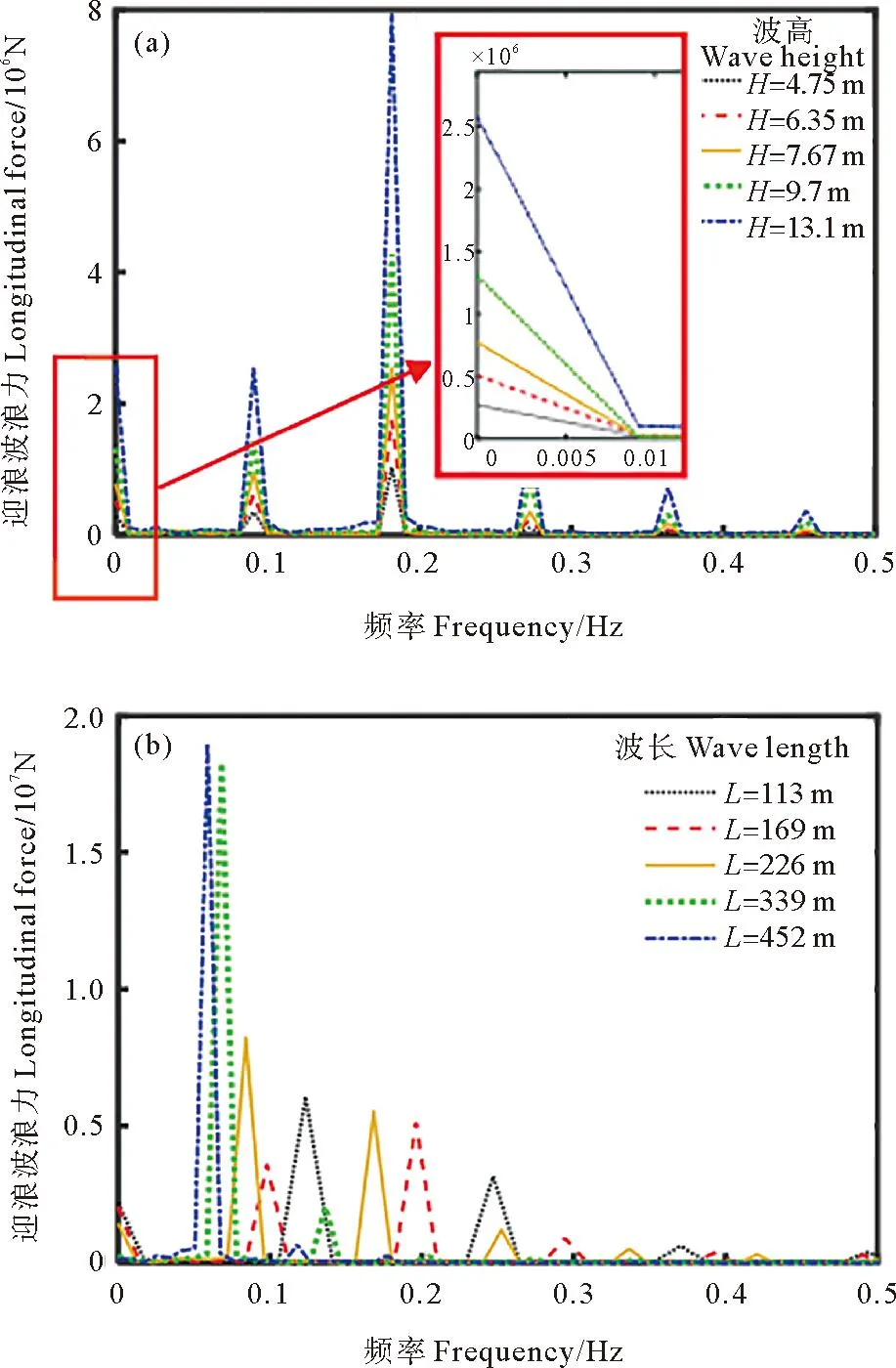
图7 迎浪波浪力的频谱图Fig.7 Frequency spectrum of the longitudinal wave forces

图8和9分别展示了平均波浪力和二倍波频力随波浪参数的变化趋势,其中的势流结果由AQWA(Advanced quantitative wave analysis)软件[17]计算得到。从图8可以看出平均波浪力和二倍波频力随波高增大呈指数增大。随着波高增大,迎浪平均波浪力的CFD仿真结果同其势流结果的误差逐渐增大,而倍波频力的CFD仿真结果同其势流结果的差异不明显。说明波高增大时,黏性效应对平均波浪力的影响明显。从图 9 可以看出,随着波长L变化,波浪力变化较为复杂。随波长增大,迎浪平均波浪力而减小,当波长L< 169.5 m 时变化速率较慢,且此时平均波浪力的 CFD结果同其势流结果有误差较大。随波长增大,二倍波频力先增大再减小;当波长接近船长时,二倍波频力达到极大值;当波长L<169.5 m 时,二倍波频力的 CFD 结果也同其势流结果有较大误差。说明当波长较短(L< 169.5 m)时,黏性效应对二阶波浪力存在明显影响。

图8 二阶波浪力随波高的变化图Fig.8 Variation of second-order wave forces with wave height

图9 二阶波浪力随波长的变化图Fig.9 Variation of second-order wave forces with wave length

3.2 FPSO的运动响应

图10展示了波高变化的工况里一个波浪周期内FPSO的垂荡和纵摇的时历曲线,时历曲线均呈现余弦函数的特征,且波高越大,运动幅值越大。

图10 波高不同工况中一个波浪周期内垂荡(a)和纵摇(b)的时历曲线Fig.10 Time history of heave (a) and pitch (b) in one time period of different wave height

图11为响应幅值算子(Response amplitude operator,RAO)随波高的变化图,其中,势流结果不随波高变化。图12为RAO随波长的变化图,RAO变化复杂,短波时的变化速率较快,长波时的变化速率较慢。可以看出垂荡的CFD结果与其势流结果吻合良好。而在波高较大的情况下,纵摇的CFD结果同其势流结果存在差异。

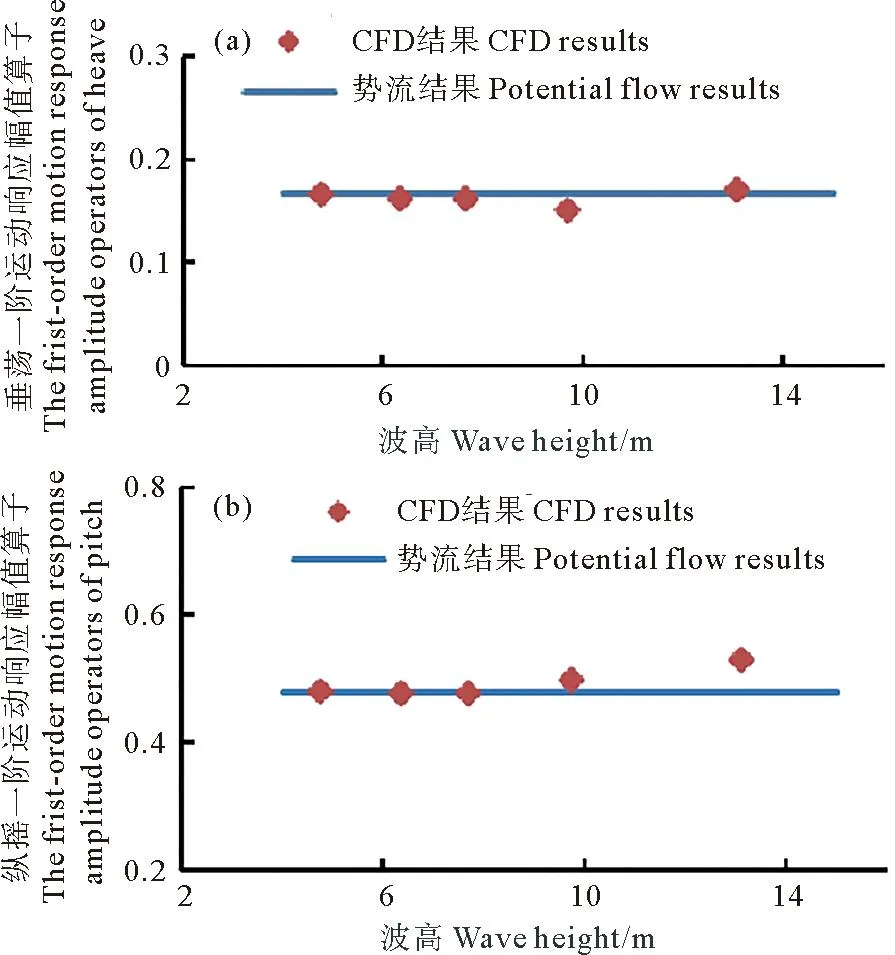
图11 RAO随波高的变化图Fig.11 Variation of RAO with wave height

图12 RAO随波长的变化图Fig.12 Variation of RAO with wave length

为定量分析黏性对纵摇的影响,本文中比较了纵摇的CFD结果和势流结果的相对误差(见表7)。小波陡情况下,CFD结果同势流结果的相对误差小于5%。当波陡H·L-1>1/15时,相对误差达到了10%以上。说明波陡较大(H·L-1>1/20)时,黏性效应对于纵摇的影响明显。

表7 纵摇运动的CFD结果和势流结果的相对误差Table 7 Relative error of pitch motion between CFD results and potential flow results %

3.3 瞬时时刻流场分析

图13以工况5为例,展示了一个周期内FPSO在流场中的运动以及自由液面的演变和压力分布的时刻图。图13中选取的时刻分别对应受力曲线极值点的时刻,目的在于直观地观察波浪入射和FPSO的运动,进而分析二者的相互影响对FPSO受力的影响。

图13 工况5的自由液面和压力分布时刻图Fig.13 Snap shots of wave pattern and pressure of condition 5

t=152.4 s时,FPSO刚运动过平衡位置,船身下沉并尾倾,此时波峰位于船首和船尾,船身压力分布均匀。船尾柱下沉过程有明显的压力集中。t=155.4 s时,FPSO的垂荡达到最大幅值,船尾柱下沉并且船首倾,此时船首遭遇波谷,使得波谷的峰值更小。波峰位于船身前中段,压力集中在此区域。t=158.4 s时,波峰即将传播到船首,使压力集中于船首并导致其下沉,而船中后段正处于波峰的位置,此区域压力数值较大。t=161.4 s时,波峰传播到船首,船身同时上浮,使得船首压力数值非常大,而船中和船尾部的压力均较小,进而使船体首、尾间的压力差非常大。

本文使用的FPSO船首为直立U形结构,而船尾为倾斜方形结构且有尾柱,二者结构的差异对流场的扰动完全不同。图13能看出船首前端的波峰和波谷都有明显增大,而船尾的流场扰动不如船首明显。图14展示了同一时刻船首、尾处的垂向截面的涡量与流线图,箭头为流线的方向。t=150 s时,FPSO正在首倾,船首处的流体流动方向不同于船尾的流体流动方向,船尾柱近壁面能看到涡量,且流线复杂。

图14 同一时刻船首、尾垂向截面的涡量场和流线图Fig.14 The vorticity and streamlines of vertical section of the bow and stern at the same time

同一时刻不同波陡条件下的水下某水平截面的涡量场(底色)和流线(黑色线条)如图15所示。随着波陡增大,船首附近的流线同FPSO近壁面的涡量场也存在差异。

综合分析,本文作者认为CFD方法可以良好地捕捉到流场的特征。FPSO在波浪中不断运动,湿表面积和船体压力不断变化,从而导致自由液面的复杂扰动,影响了受力的非线性。在大波陡情况下,船首波浪叠加现象明显,自由液面复杂,船首流场同船尾流场有明显差异,导致黏性效应对波浪力和纵摇运动的影响显著。

4 结论

(1)考虑黏性的CFD方法较之势流理论会高估平均波浪力。波高越大或者波长越短,黏性效应越强,从会导致CFD结果和势流结果的差值差异化增大。

(2)规则波作用下FPSO受力呈现非线性的原因:入射波与FPSO运动相互影响导致自由液面的复杂变化;FPSO运动时湿表面积和压力分布不断变化。

(3)由于船首结构不同于船尾结构,导致流场扰动出现明显差异,当波陡达到1/15,CFD结果与势流结果的误差达到10%。说明在非线性较强的情况下,黏性效应对纵摇运动影响明显。