核心素养视域下的初中数学大单元教学研究

【摘要】文章以人教版初中数学教材方程的相关知识为例，针对如何建立大单元系统、设定教学目标、开展梯度性教学活动等问题，分析核心素养视域下的方程大单元教学策略，以期帮助一线教师开展教学实践。

【关键词】核心素养；初中数学；大单元教学

【基金项目】本文系明溪县基础教育科学研究2023年立项课题“核心素养下初中数学大单元教学目标具体化教学点研究”（课题编号：mxjykt-2308）的研究成果。

作者简介：张火生（1973—），男，福建省三明市明溪县城关中学。

大单元教学是相对课时教学、单元教学提出的一种教学模式。大单元教学之大，体现在内容与结构方面，即整合同一主题或概念下的多个知识点，加强课时或单元间的逻辑联系开展结构化教学。

一、建立大单元系统

目前，初中数学教材虽然具有一定的逻辑性，但是没有全面体现知识内容的密切联系，故而对学生系统地学习和掌握知识技能造成一定的限制。以人教版教材为例，其在编排具体内容时，一般按照内容难度，将初中数学知识技能分散在七至九年级，导致同一主题或概念下的知识技能脱节。教师若始终按照教材逻辑进行教学，先分散讲解知识技能，到总复习阶段再指导学生进行整体复习，难免造成学生学习的碎片化，不利于学生整体掌握数学知识和发展数学学科核心素养。

在大单元教学中，教师应打破教材的编排限制，全面分析教学内容，整合具有密切联系的知识技能，建立大单元系统［1］。教师首先可提炼初中数学知识的概念或主题；其次在概念或主题的引领下，全面分析六册教材；最后跨教材与单元，整合知识技能。

比如，方程属于初中数学数与代数的领域，它既是一个重要的数学概念，也是一个独立的知识技能主题。教师应在初中阶段，通过一元一次方程、二元一次方程组、分式方程、一元二次方程的教学，促进学生对方程知识技能的掌握，使学生领会方程思想。教师还应分析每册教材中有关方程的具体教学内容，整合关键知识技能，建立大单元系统。

人教版数学七年级上册第三章的教学内容为一元一次方程，主要包括一元一次方程及其相关概念、解法、实际问题等，始终渗透数学建模与化归思想。人教版数学七年级下册第八章的教学内容为二元一次方程组。在本质上，二元一次方程组是两个含有不同未知数的一元一次方程的组合。人教版数学八年级上册第十五章包括分式方程的内容，其以分式方程的基本解法为重点。解答分式方程，可将其化为一元一次方程。人教版数学九年级上册第二十一章的教学内容为一元二次方程，围绕含有一个未知数，但未知数项的最高次数为2的方程展开。解答这样的方程，需要将其转化为一元一次方程。由此可见，一元一次方程是整个初中方程知识技能的基础。二元一次方程、分式方程、一元二次方程，都与一元一次方程密切相关，是一元一次方程的升级。教师可结合以上分析，建立方程大单元系统，完善大单元教学设计。

二、设定教学目标

建立大单元系统后，核心素养视域下的初中数学大单元教学可循序渐进地开展。教学目标是顺利开展教学的前提之一。核心素养视域下的教学，应以核心素养为导向，设定教学目标，提出具体的学生发展要求。教师应分析有关方程知识的核心素养，使教学目标详细、清晰、有层次。方程大单元的教学目标如下。

直观想象目标：根据直观情境领会方程概念，通过想象学会判断等量关系，确定不同方程的相同点和不同点。

数学抽象目标：在具体情境中提取方程信息，确定等量关系，列出正确形式的方程。

逻辑推理目标：经历类比分析、分类讨论等逻辑过程，发现并总结不同方程的求解方法，感受方程思想、转化思想、归一思想等。

数学运算目标：在求解方程期间，提高数学运算的准确性。

数据分析目标：结合方程问题对应的具体数据，加强数据分析，总结数据规律，提高数据分析意识和相关能力。

数学建模目标：构建解决各种方程问题的数学模型，同时运用该模型解决不同的实际问题。

目标明确地指示学生应在方程大单元中的学习内容与预期成果，有利于教师指导接下来的教学活动，也有利于学生自觉设计指向核心素养的大单元学习计划。

三、开展梯度性教学活动

初中数学课程以逻辑性与抽象性为主要特点。在大单元教学模式下，有机整合同一概念或主题下的知识内容，可能会增强教学内容的逻辑性与抽象性，加大学生的学习难度。为使学生顺利达成核心素养的发展目标，教师需要采取梯度性指导策略，以循序渐進、由浅入深为基本原则，适应学生螺旋上升的发展规律。

（一）趣味性教学活动

大单元教学具有挑战性，教师与其向学生直接灌输知识技能，不如使其以学习为乐［2］。为此，教师应以趣味性教学活动为抓手，根据方程大单元特征，巧妙应用情境与游戏。比如在方程大单元的一元二次方程教学阶段，教师可联系一元一次方程的内容设计情境与游戏，并将其在教学导入环节加以应用。

1.情境教学

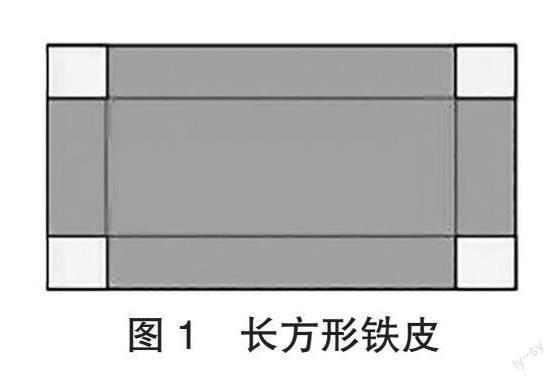
初中数学一元一次方程、二元一次方程组等内容具有情境性，要求学生在真实问题中抽象出方程概念。教师可立足方程的用途，为学生创设真实的问题情境。比如，教师创设“制作无盖铁盒”情境：如图1所示，有一块长100厘米、宽50厘米的长方形铁皮，在铁皮的四角各切一个正方形，然后将四周多余的部分折起来，就能制作一个无盖铁盒。如何使这个铁盒的底面积为3600平方厘米？

2.游戏教学

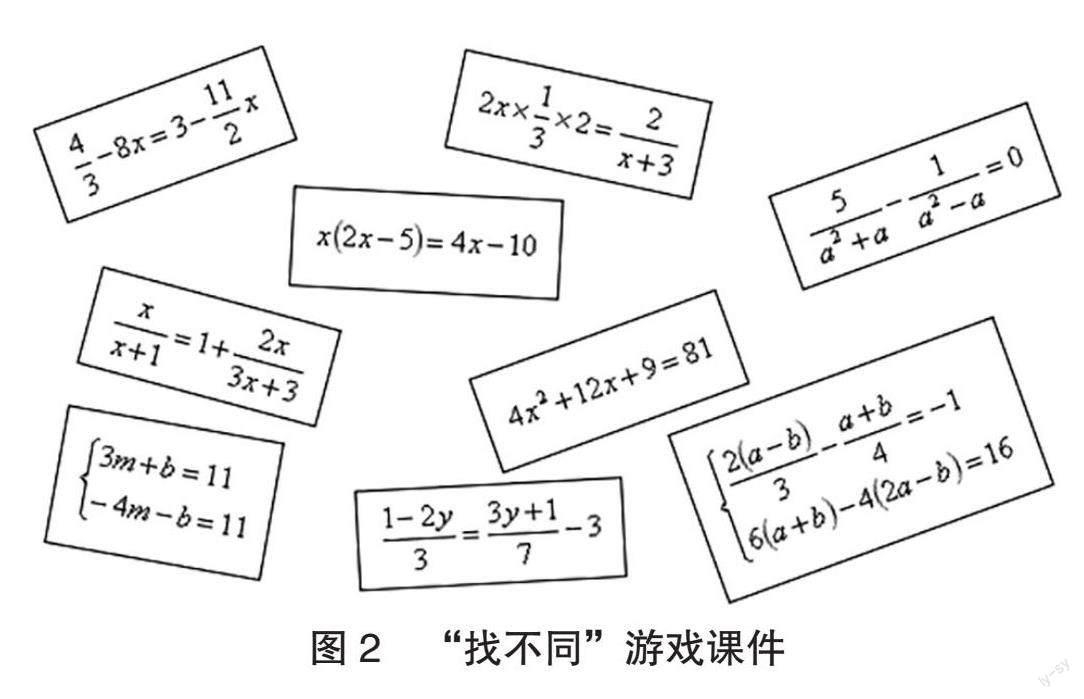
教师可结合方程大单元知识技能的内在联系，设计“找不同”游戏。游戏设计思路如下：教师整理一元一次方程、二元一次方程组、分式方程、一元二次方程的典型算式，打乱其呈现顺序，使学生迁移已有知识“找不同”，归类已学知识技能，从中发现一元二次方程的特殊性，提出概念、性质、求解方法等猜想。比如，教师整合教材的方程教学资源，出示游戏课件（如图2所示）。

课件包括一元一次方程、二元一次方程组、分式方程、一元二次方程等，但无呈现规律可循。教师向学生提出游戏要求，说明游戏规则，鼓励学生观察、对比、筛选课件的信息，这样既能活跃课堂，又能促进学生主动学习方程的知识内容。教师还可为学生计时，以此营造紧张的游戏氛围，增强学生思维的活跃性。

（二）思维点拨

问题是教师点拨学生思维常用的工具。教师应点拨学生的思维，使其在更深层次上思考方程问题，并且得到正确的结果。一方面，教师应重视“师问”的重要价值；另一方面，教师要充分认识“生问”的必要性，使学生发挥质疑的作用。

1.教师提出启发性问题

教师利用“师问”点拨学生，应以启发性问题为主。启发性问题可激活学生的内在学习动机，强调学生经历充分的思维活动。启发性问题在初中数学大单元教学中的应用，对学生的结构化学习起着重要的促进作用。教师可根据学生学情与大单元教学目标，设计差异化的启发性问题，从而有针对性地点拨学生的思维［3］。

比如，在上述“制作无盖铁盒”情境中，教师可以提出以下启发性问题。（1）结合题意分析，情境中的未知数和等量关系分别是什么？（2）根据之前的学习经验回答，用含有未知数的等式表示等量关系的算式属于什么？（3）你之前学习的方程知识技能能否解决情境问题？如果不能，你有更好的解决办法吗？

问题由浅入深，启发学生将从情境中抽象出的方程知识与之前学过的内容建立联系。通过环环相扣的问题引领，学生发现，一元一次方程、二元一次方程组、分式方程均无法解决此情境问题，必须探究新的方程形式，即一元二次方程。学生在此基础上尝试设未知数列方程，自主经历一元二次方程的探究过程，有利于促进直观想象、数学抽象等素养的发展。

2.学生提出质疑

教师可鼓励学生质疑，以质疑为抓手，点拨学生的数学思维。比如，在上述“制作无盖铁盒”情境中，学生迁移方程大单元的其他知识技能，基本能够设“切掉的正方形边长”为未知数 x，列出方程（100 -2 x）（50-2 x） =3600。但是，将方程化简为5000 -300 x + 4 x2=3600后，许多学生开始犯难。“这个方程看上去很特殊，怎样求出这种方程的未知数？”“分式方程是之前学过的特殊方程，它可以转化为一元一次方程，然后求解。这个方程也能这样做吗？”此时，教师可点拨学生：“也许一元一次方程真的可以用来解决眼前的问题，何不试一下呢？试着将5000 -300 x + 4 x2=3600化简吧，看看它能否变成一元一次方程的相关形式。”在教师的点拨下，学生可尝试在一元一次方程与一元二次方程之间建立联系，发展逻辑推理与数学运算素养。

（三）实践探究

通过教师的点拨和适当的补充讲解，学生基本能够掌握解一元二次方程的方法，如直接开方法、公式法、因式分解法等。此时，为进一步助力学生开展大单元学习，教师应为学生搭建实践探究平台，鼓励学生全面应用知识技能。教师可立足生活设计问题，提出综合性、开放性等实践探究任务，鼓励学生“做中学”，内化知识技能［4］。比如，教师可提出如下综合实践问题。

为促进当地旅游经济的发展，A市提出一系列旅游优惠政策。该政策提出以来，当地接待游客的人数逐月增加。据不完全统计，八月份游客为4万人，十月份游客为5.76万人。求八月份到十月份之间，该市游客人数的月增长率。已知该市仅有两个景点，但有三种购票方式：第一，单独购买景点一门票，每张100元；第二，单独购买景点二门票，每张80元；第三，购买景点一与景点二的套票，每张160元。大数据预测十一月份该地游客人数约7万人，其中约2万人选择第一种购票方式，3万人选择第二种购票方式，2万人选择第三种购票方式。当单票价格不变时，套票价格每下降1元，将有600名原计划采用第一种购票方式的游客和400名原计划采用第二种购票方式的游客改为购买套票。假设十一月份当地两个景区总收入为Q万元，套票下调P元，写出Q与P的表达式。若当地预期十一月旅游收入为798万元，则套票价格应下调多少元？

上述综合实践问题考查学生对一元二次方程的理解，更考查学生对方程思想的迁移应用。学生可先自主对问题进行分析，再合作探究问题，发展逻辑推理、数学运算、数据分析等核心素养。

（四）思维导图

思维导图的可视化功能有助于学生整体梳理大单元知识技能，建构系统化知识体系。教师应在学生完成实践探究任务后，借助思维导图指導学生整体回顾，总结归纳知识技能［5］。

教师可根据大单元概念或主题设计思维导图主题词，鼓励学生自主绘制思维导图，填写重要信息，同时进行分享交流。教师可先为学生示范思维导图的绘制方法，再引导学生整理一元一次方程、二元一次方程组、分式方程、一元二次方程等知识技能，促使学生梳理知识脉络，增强数学技能，丰富数学建模经验。

结语

在核心素养视域下，教师应加强初中数学大单元教学的相关研究，发挥大单元教学的作用，促进学生数学学科核心素养的发展。

【参考文献】

［1］王婷婷.核心素养视域下的初中数学大单元教学［J］.天津教育，2022（28）：72-74.

［2］王志华.初中数学“单元—课时”教学实践与思考［J］.数学教学通讯，2022（5）：44-45.

［3］邢成云，陈元云.课程整合视域下培养学生数学核心素养的大单元教学：以方程大单元为例［J］.中小学课堂教学研究，2021（12）：19-23，27.

［4］屠卓娅.大单元教学：实现数学教学设计与学科素养的有效对接［J］.求知导刊，2021（37）：56-57.

［5］郑旗.初中数学方程大单元教学的研究［J］.学苑教育，2021（18）：59-60.