数学教师专业成长的四个层面——以教材函数习题为例

何建东, 俞菊妃

(1.绍兴市越州中学,浙江 绍兴 312075;2.绍兴文理学院数理学院,浙江 绍兴 312000;3.绍兴市元培中学,浙江 绍兴 312000)

数学教师不仅要在教学中加强对解题方法和数学思想的落实,而且要在教学过程中重视教学理论与教育德育的渗透[1].在发展解题能力、融合数学思想、组织有效教学、贯彻数学育人这4个递进式层面,数学教师既可以达到“固本”“探源”两个教学目标,更能够使自身实践与理论得到双重专业成长.

章建跃在人教A版《普通高中教科书·数学》(以下统称“高中《数学》”)扉页“寄语”中指出,仔细阅读教科书,用心揣摩每句话,弄懂每道例题,在探究、质疑、反思中逐渐领悟数学概念及其蕴含的数学思想和方法[2].《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)也明确指出,数学课程要体现现代数学的本质,充分认识数学教育的育人功能,数学教学应以发展学生数学学科核心素养为导向,创设合适的教学情境,启发学生思考,引导学生感悟数学的科学价值、应用价值、文化价值和审美价值[3-4].

以高中《数学》(必修第一册)“函数的概念与性质”单元教学为例,我们首先要明晰“函数是贯穿高中数学的一条主线,因其抽象程度高而成为许多学生的学习难点”;其次要明白“用好、弄透教材的每道例题和习题,才能帮助学生准确把握函数的概念及其思想方法”;然后要明确“理解《课标》要求,落实教材内容,发挥课堂功能,引导学生通过例题和习题去感受数学文化、解决数学问题、形成数学思想”[5].

1 解题有“法”——半亩方塘一鉴开

问题是数学的心脏．好的数学问题不仅可以触发学生的数学思考,而且可以成就一段教学“佳话”．尤其是教材中的例题和习题,都是专家精挑细选的,凝聚着编写团队的智慧与心血．数学教师要用好、弄透每道例题和习题,引导学生分析解决,做到解题有“法”．

例1证明:

1)若f(x)=ax+b,则

2)若g(x)=x2+ax+b,则

(人教A版高中《数学》(必修第一册)第101页综合运用第8题)

分析这是笔者经常用作例子的教材习题．通过对该题的解答,既可以复习初中已学的一次函数和二次函数的图象与性质,又可以让学生熟悉巩固高中新学的函数符号f(x)的含义．教师还可以引导学生既着眼于“代数”的角度,通过“解析式”的演算严格推理论证,又借助“图象”的角度,通过“函数特性”直观简洁感知．

证明(代数角度)

1)因为等式左边为

等式右边为

所以

2)因为等式左边为

等式右边为

感知(图象角度)如图1、图2所示.

图1 图2

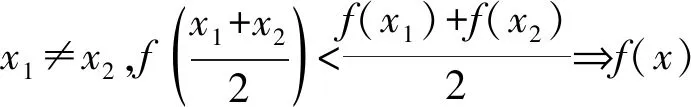
基于以上问题的解决与说明,笔者一般会通过适当地变化与引用,让学生思考解决如下类似的问题.

( )

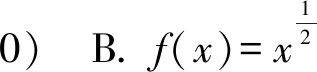
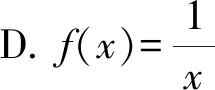
答案为BC.

2 数学求“理”——天光云影共徘徊

数学是系统的学科．无论是数学问题还是数学方法,都不是孤立存在的．数学教师除了要引导学生解决问题,也要适时适切地引领学生梳理蕴藏在问题中的数学思想,将研究的重点内容系统整合成规律化的模块,以“问题链”“结论堆”的形式呈现,养成数学求“理”的习惯．

以上述教材习题为引子,教师可以做两方面“理”的探求.

一是系统地归纳整理教材中涉及函数单调性、奇偶性、最值等图象与性质的系列例题和习题,对“函数的图象与性质”进行拓展研究,引领学生逐层得出如下系列“结论堆”.

1)f(0)=0⟹f(x)过原点.

2)f(-x)=f(x)⟹f(x)为偶函数;f(-x)=-f(x)⟹f(x)为奇函数.

3)任意x∈D,f(x)≤M,存在x0∈D,f(x0)=M⟹M为f(x)的最大值;任意x∈D,f(x)≥M,存在x0∈D,f(x0)=M⟹M为f(x)的最小值.

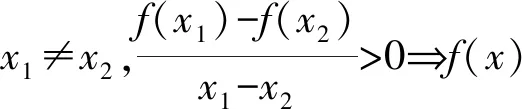
5)f(x+1)=f(x)⟹f(x)的周期为1.

6)f(1+x)=f(1-x)⟺f(x)=f(2-x)⟹f(x)的图象关于直线x=1对称;f(1+x)=-f(1-x)⟺f(x)=-f(2-x)⟹f(x)的图象关于点(1,0)对称.

7)f(x)+f(-x)=2⟹f(x)的图象关于点(0,1)对称;f(a+x)+f(a-x)=2b⟹f(x)的图象关于点(a,b)对称.

8)f(x+y)=f(x)+f(y)⟹f(x)的一个代表函数为f(x)=kx(其中k≠0);f(xy)=f(x)·f(y)⟹f(x)的一个代表函数为f(x)=xα(其中α为常数).

10)|f(x)|的图象可看作f(x)的图象保留x轴上方部分,同时将x轴下方部分图象沿x轴翻折到x轴的上方;f(|x|)的图象可看作f(x)的图象保留y轴右侧部分,擦去y轴左侧部分,同时画出y轴右侧部分图象关于y轴的对称图象;f(x-1)+2的图象可看作f(x)的图象向右平移1个单位,向上平移2个单位得到．

二是将数学的观点站得更高些,利用教师学过的高等数学知识,揭示教材例题和习题背后的数学知识,如本文例1的“源头”是高等数学中的“琴生不等式”.

琴生不等式设函数f(x)的定义域为I,任意x1,x2∈I,其中x1≠x2,λ∈(0,1),总有

f(λx1+(1-λ)x2)≤λf(x1)+(1-λ)f(x2),

则称f(x)是区间I上的凸函数(《数学分析》中也称“下凹函数”);反之,如果总有

f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),

则称f(x)是区间I上的凹函数(《数学分析》中也称“上凸函数”).

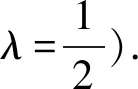
3 教学悟“道”——问渠那得清如许

教学是范式的行为．数学教学往往有“范式”可循,数学教师要组织学生悟得学习中的门道——研究程序．以“函数”为例,何为函数?为何要研究?怎么研究?中学数学就是在不断研究解决各模块内容的这3个问题,从而贯彻《课标》,使用教材开展课堂教学,实现教学悟“道”.

为了给不同数学内容的教学提供借鉴,笔者以“函数的图象与性质”为例梳理得出教学的一般研究范式.

1)我们已经储备了函数学习的哪些基础知识?(初中阶段学过的函数知识:正比例函数、一次函数、反比例函数与二次函数等.)

2)搜集、了解函数的形成与发展史.(函数产生的社会背景、函数概念发展的历史过程、函数符号的故事、数学家与函数等.)

3)举例说明数学问题中的函数背景素材.(融合在数学教材大量例题和习题中的数学历史文化、社会科技文化、现实生活文化中的背景材料.)

4)研究函数图象与性质的一般化路径.(从函数定义域入手,经由函数的奇偶性、单调性、对称性、周期性、特殊点线,借助图象,最后到函数的最值与值域.)

(人教A版高中《数学》(必修第一册)第79页例3)

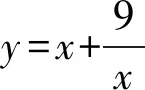
(人教A版高中《数学》(必修第一册)第86页综合运用第8题)

(人教A版高中《数学》(必修第一册)第92页探究与发现)

(人教A版高中《数学》(必修第一册)第101页拓广探索第12题)

2)对函数解析式中的实数a,b,你认为需要分哪些情况进行讨论研究?这些情况之间有何内在的联系?

3)这种类型的函数的研究过程中,与基本不等式存在怎样的关联?如何解释说明函数单调区间的分界点?

通过这个学习、联系、研究与转化的过程,学生可以提升自己对数学的研习能力,教师的数学教学也更上了一个台阶,突出了教学的本质与关键．

4 教育立“德”——为有源头活水来

立德是教育的根本．教育要回答并解决“为谁培养人?培养什么人?怎么培养人?”的问题.处于基础教育与高等教育关键过渡的中学,更要坚定不移、不折不扣地“立德树人”.数学教师要充分领会、深入理解并贯彻落实《课标》的“德育”全要素,落实教育立“德”．

新教材一个显著的特点就是整合了大量内容丰富、形式多样的数学文化背景材料,广泛渗透在教材的例题、习题和阅读材料中．数学教师在理解利用教材例题、习题的过程中,除了要充分揭示数学的内在本质属性,还要善于发掘并阐述蕴含在数学各方面的“德育素材”,包括教材每章的引言、每节的例题习题、每单元的阅读材料、每阶段的探索与发现等．教师不仅要引导学生解决数学问题,以发展和提升数学素养,更要引领学生探寻数学问题的来源与发展,以感悟数学的“文化自信”,让数学教学始终“德育”其中．

笔者通过“函数的概念”的3个引例进行数学“德育”(以下引例中的图和表略).

引例1某“复兴号”高速列车加速到350km/h后保持匀速运行半小时．这段时间内,列车行进的路程s(单位:km)与运行时间t(单位:h)的关系可以表示为s=350t．

(人教A版高中《数学》(必修第一册)第60页问题1)

引例2如何根据某市某日的空气质量指数(Air Quality Index,简称AQI)变化图确定这一天内任一时刻t的空气质量指数(AQI)的值I?你认为这里的I是t的函数吗?

(人教A版高中《数学》(必修第一册)第60页问题3)

(人教A版高中《数学》(必修第一册)第60页问题4)

分析上述3个引例中,引例1以我国自主设计的高速动车为科技文化背景,彰显“中国速度”“中国智造”,而且可以让坐过或者没坐过“复兴号”动车的学生感知和了解“350”是个什么概念.当我们坐着自己国家设计制造的高速动车驰骋在祖国绿水青山之间,是何等的自豪与爽快!引例2以与人们日常生活息息相关的空气质量为社会文化背景,着眼当前国际国内特别关注的人类环境保护话题,与我国下一个百年大计中的“碳达峰”“碳中和”目标相契合,反映了我国不仅要建设一个强大的社会主义国家,更要建设一个在国际社会中负责任的“大国形象”．引例3将事关我国城镇居民生活质量的恩格尔系数作为社会文化背景,寓意“人民至上”的发展理念,反映了我国社会文明建设的主要目标是实现全面小康,满足全体人民对更加美好生活的向往,可见教材的例题和习题的“小题目大作为”．

数学的教与学,如科学研究,亦如文化表达,既需要有“横看成岭侧成峰,远近高低各不同”那样,善于从不同的角度、不同的层次去分析探究,以品味其中所蕴含的味道,更应该秉持“素心正如此,开径望三益”的精神,回归数学最本质、最朴素的东西,方能以不变应万变,以其宗驭其形[6-7].