项目学习中发展数学“三会”
——以“变装的易拉罐”为例
景昱波, 戴秀梅
(1.杭州市观成武林中学,浙江 杭州 310000;2.杭州市拱墅区教育研究院,浙江 杭州 310000)
《义务教育数学课程标准(2022年版)》提出,在数学学习过程中,学生不仅需要获得“四基”,提升“四能”,还需要培养“三会”的核心素养[1].核心素养的培养需要教师更新教学方式,而数学项目学习正是重要的载体.其以真实问题解决为导向,整合数学与其他学科的知识和方法,让学生从数学的角度观察与分析、思考与表达、解决与阐释现实生活现象,体会数学的价值,发展应用和创新意识.数学项目学习的特征可概括为:情境的真实性、问题的挑战性、过程的完整性、成果的创新性、学科的融合性[2].但如何设计和实施核心素养导向下的数学项目学习,对一线教师来说仍存在困难.
本文基于对核心素养导向下的数学项目学习的理解,开展案例实践,并给出相应的教学思考,意在为一线教师的项目学习教学提供借鉴.
1 项目前期分析
1.1 项目内容
生活中有两种不同的易拉罐,二者容量一样,价格不同,学生自然会提出驱动性问题“为什么价格不同”.学生通过小组交流,自主提出两个研究思路:1)价格不同可能和包装用料相关;2)价格不同可能和外观设计相关.在问题的分析与解决过程中,促使学生将现实生活与数学建立联系,通过建立数学模型来解决问题.本项目融合数学、物理、美术等学科,以跨学科的形式进行学习,打破学科界限,学生在项目学习过程中,完善知识结构,提升综合应用能力,从而发展核心素养.基于以上分析,本项目的教学重点是:建立现实问题与数学的联系,利用数学建模解决问题.
1.2 学情分析
本项目实施对象是九年级学生.在知识能力上,学生已经学习过圆、黄金比以及函数等相关知识,具备相应的基础知识.在探究能力上,学生具备合作学习的活动经验.但学生在数据测量时不够严谨;在模型推导过程中容易出错,以及对如何建立模型和研究函数模型存在疑问.基于以上分析,本项目的教学难点是:数学模型的建立与利用模型分析问题.
1.3 学习目标
1)通过比较不同易拉罐的价格和外观,从数学角度分析和思考,培养学生数学分析的能力;
2)通过建立数学模型和制定假设解决问题,培养学生解决问题的能力;
3)通过不断优化模型,对模型的准确性进行评估,培养学生的实践意识和反思能力;
4)通过设计易拉罐的外观,激发学生的创造力和创新思维.
1.4 教学活动结构设计
项目学习对初中生来说是新鲜的,学生会怀有很大的热情,对此教师需要围绕驱动性问题和学习目标制定教学活动.在教学活动中应鼓励学生以小组合作的形式,亲历发现、提出、分析、解决问题的过程.
本项目的教学结构如图1所示:

图1
2 项目实施过程
2.1 真实情境,问题驱动

图2
在超市购买饮料时,可选择如图2所示的摩登罐或普通罐,二者饮料容量都是330 ml,而摩登罐(图2(a))3元/罐,普通罐(图2(b))2.5元/罐.
问题1通过这个真实情境,你认为我们可以研究什么?
师生活动在了解了情境后,自然会提出驱动性问题“为什么价格不同”.
问题2请同学们先独立思考,再以小组讨论的方式想想导致二者价格不同的原因.
师生活动学生通过交流得到2个统一的研究思路(假设饮料成份相同):
1)价格不同可能和包装用料相关;
2)价格不同可能和外观设计相关.
教学说明学生基于真实情境,自主提出驱动性问题,这一过程是培养学生“如何从数学的角度发现和提出问题”的最佳路径.随后学生通过独立思考与合作交流,进一步提出该问题的研究思路,为后续“如何从数学的角度分析问题和解决问题”指明方向.
2.2 问题分析,提出假设
问题3先从思路“价格不同可能和包装用料相关”展开研究,你认为怎样用料会导致价格不同?
师生活动学生认为在容量相同的情况下,可能与用料的材质或多少相关.
教师可组织学生查阅相关资料,从资料中可知2种易拉罐的材质都是铝合金,于是确定价格不同可能和材料用量不同相关.
问题4如何获得2种易拉罐的铝合金材料用量?
师生活动师生共同探讨,制定方案.
方案1学生对易拉罐的高、直径、厚度进行测量,分别计算用料体积、质量和价格.
方案2学生通过称一称获得用料的质量,计算价格.
2.2.1 方案1的实施过程
追问1在测量的过程中会遇到什么困难?
学生提出以下困难:
1)易拉罐并非标准圆柱体,在罐身与上下底面连接处存在弧形,且上下底面的形状不同;
2)易拉罐底面直径的测量存在难度,需确保所测弦过圆心;
3)易拉罐的厚度不易测量,并且罐身与上下底面厚度不同.
结合实际情况提出模型假设:
1)假设2种易拉罐都是圆柱体;
2)假设易拉罐均由相同的铝合金材料制作;
3)假设易拉罐的上下底面都为圆形,且形状大小无差别;
4)假设易拉罐罐身的厚度相同,上下底面的厚度相同.
方案1中的符号说明如表1所示:

表1 方案1中的符号说明
教学说明学生通过查阅资料明确研究对象.师生共同探讨制定2种研究方案.进一步,学生思考方案1数据测量过程中的问题,从而提出合理假设,用符号表示,并为后续建立模型奠定基础.
问题5结合大家提出的测量过程中的困难,该如何测量高度、直径和厚度?
师生活动学生很容易获得高度,并通过小组合作获得了如下4种测量底面直径的思路:
思路1将罐底描在纸上,利用圆的轴对称性,对折即可.
思路2利用圆的周长公式C=πd,将纸绕罐身一圈测量周长,求直径.
思路3利用圆周角定理的推论(90°的圆周角所对的弦为直径)确定直径.
思路4利用三角板与直尺制作简易卡尺,测量直径.
最终通过查阅文献资料获得易拉罐的制作工艺和材料厚度.
方案1中的数据结果如表2所示:
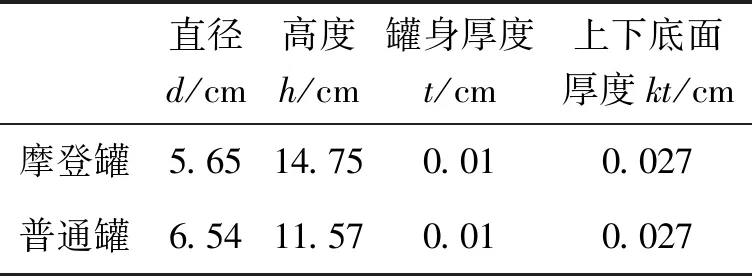
表2 方案1中的数据结果
模型建立由圆柱体的底面半径r、高h、罐身厚度t、上下底面厚度kt,计算用料体积
V=2πr2kt+2πrht;
(1)
由铝合金的密度ρ,计算制作用料质量
m=ρV;
(2)
最后结合铝合金的单价P,可得用料总价
W=Pm.
(3)
问题6在利用模型解决问题前,还需要什么数据?
师生活动学生查阅资料可得铝合金密度为2.7 g/cm3,单价为25元/kg.
学生将数据代入模型,结果如表3所示:
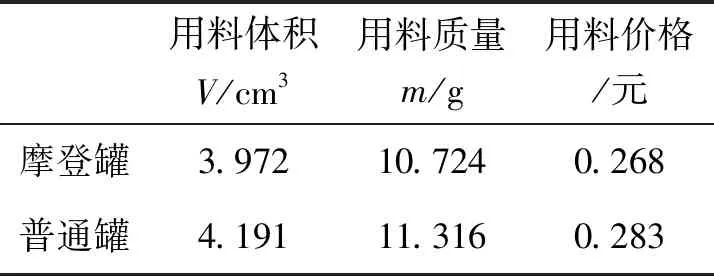
表3 代入模型后的结果
2.2.2 方案2的实施过程
学生通过称重,得到数据结果如表4所示:

表4 方案2的数据结果
结论1普通罐的铝合金用料价格反而比摩登罐的高,可知摩登罐比普通罐定价高和用料无关.
教学说明本环节是对研究思路1的探究.学生通过查阅资料或是小组讨论获得数据,通过数学模型得到摩登罐比普通罐定价高和用料无关的结论.教师在教学过程中需通过有效问题进行引导,并给学生思考与交流的时间,学生定将还教师无限的可能.
2.3 优化模型,解决问题
问题7再从“价格不同与外形设计理念相关”展开研究,摩登罐的设计特殊在哪里?
师生活动学生通过独立思考与小组交流,获得如下2种想法:
想法1摩登罐的长、宽比例更加协调,符合大众的审美.
想法2由于摩登罐的用料比普通罐少,说明在材料的利用率上更高.
问题8结合所测数据,思考摩登罐的长、宽比例为何更加协调,其背后是否蕴含数学知识?
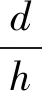
问题9能否利用数学知识说明摩登罐的设计材料利用率更高?
师生活动利用所测数据,计算发现摩登罐的实际容量L1=370 ml,而普通罐的实际容量L2=389 ml.因此,摩登罐的空间利用率高于普通罐.
追问2当摩登罐的实际容量固定时,易拉罐的高度h与底面半径r是否具有函数关系?
追问3能否将模型(1)转化成V关于r的函数模型?利用函数模型说明摩登罐的设计更有优势.
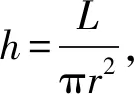
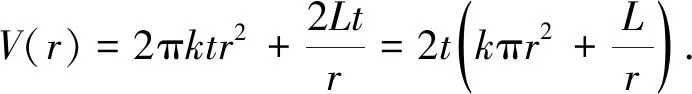
(4)
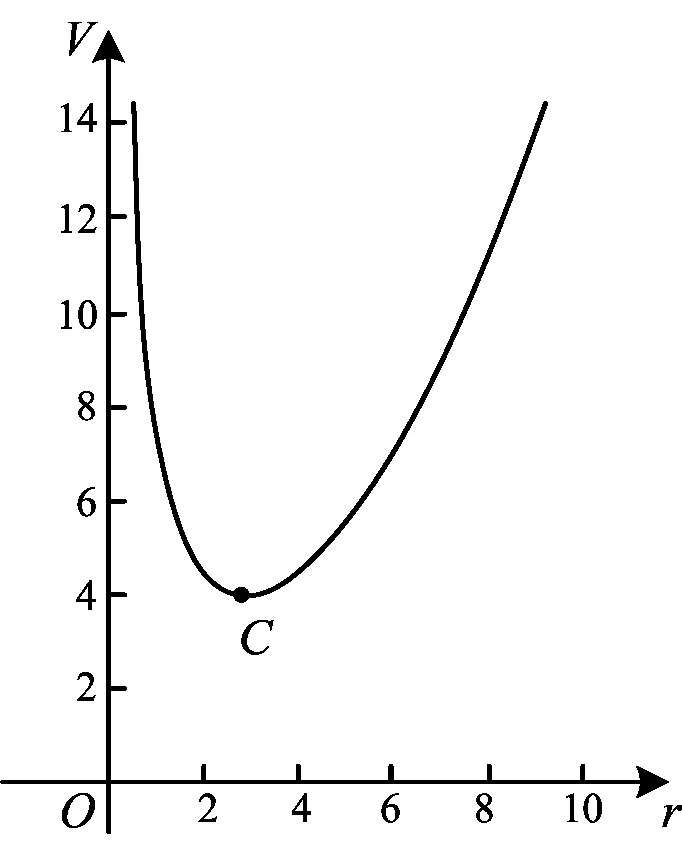
图3
将摩登罐的数据带入函数模型,学生利用GeoGebra软件绘制函数图象(如图3),并找到相应的极值点C的横坐标为r=2.794,可知其近似等于摩登罐的半径2.825,因此摩登罐的设计是在以实际容量为370 ml基础上的最优设计.
教师可适当普及高中知识,利用导函数得到极值点的横坐标.对原函数求导可得

利用摩登罐的数据验证:摩登罐在实际容量为370 ml且k=2.7时,最优解为r=2.794,h=15.08,这与实际r=2.825,h=14.75接近,因此摩登罐的设计符合最优尺寸设计.
结论2摩登罐不仅设计理念与黄金比相关,且在用料上少于普通罐,材料利用率和空间利用率更高.利用函数模型也可求得摩登罐的设计接近最优尺寸设计,设计理念更加环保.因此,师生一致认为摩登罐定价高,是因为隐藏其中的设计价值.
教学说明本环节是对研究思路2的探究.学生思考交流得到2种想法,通过分析测量数据发现设计理念与黄金比相关;再从材料利用率着手,将已有模型转化成函数模型,运用软件绘制函数图象,研究函数性质,符合函数学习的一般思路,真正做到学以致用;随后教师立足高观点,利用函数模型分析最优设计,并验证摩登罐接近最优设计.在教学过程中教师需引导学生解释数学结论的现实意义,从而解决驱动问题.
2.4 交流展示,迁移应用
为了进一步巩固项目学习中获得的经验与方法,将成果进行课后延伸,教师需要布置与项目学习相关的子任务给学生课后研究学习.本项目教师给出了2个子任务“黄金比在生活中的应用”与“能否设计一款300 ml液体容量的易拉罐使得材料最省”,这2个子任务的完成有助于提升学生综合素养和数学建模的能力,发展创新意识与应用意识.
子任务1的交流展示学生自主完成“黄金比在生活中的运用”作业,并组织班级内交流展示.发现黄金比主要涉及以下内容:
1)人体结构.人体结构中有许多比例关系接近0.618,如人有20颗乳牙、32颗恒牙,其比例接近黄金比;人的正常体温37℃,而人在24℃的环境下新陈代谢和生理机能都处于最佳状态,其比例也接近黄金比.
2)自然现象.有些植茎上,2张相邻叶柄的夹角是137°28′,圆周是360°,360°-137.5°=222.5°,而137.5∶222.5≈0.618,研究发现,这种角度对植物通风和采光效果最佳.
3)艺术创作.西方艺术家非常注重把和谐的比例关系融入艺术作品中.例如,名画《蒙娜丽莎的微笑》《维特鲁威人》.又如,著名的雕塑《维纳斯》《大卫》.
4)建筑设计.帕特农圣庙的外部建筑结构完全按照黄金矩形设计,给人庄严肃穆的感觉和美的享受.埃及金字塔、上海东方明珠塔、埃菲尔铁塔等都符合黄金比例.
5)工业设计.以logo设计为例,许多品牌的标志均利用黄金圆环进行设计,如苹果手机、麦当劳等.
子任务2的迁移应用学生在研究子项目2“能否设计一款300 ml液体容量的易拉罐使得材料最省”时自主提出了以下3个问题:
1)为什么易拉罐的设计都是圆柱形的,而非立方体形状?
2)为什么易拉罐的实际容量要高于液体容量?
3)如果采用更先进的制作材料和工艺,会不会用料更省?
评注采取小组合作的形式展开交流:对于问题1),从数学角度可知,平面中等面积情况下,圆的周长最小,于是在等体积的柱体情况下,横截面为圆形用料最少;从物理角度可知,易拉罐多数装碳酸饮料,当受到外力时,圆形的表面受力均匀,不易变形,方便运输.
对于问题2),碳酸饮料在运输过程中,摇晃会产生膨胀,为其预留一定的气体空间较为合理,这也是为何易拉罐实际容量要大于液体容量的原因.
学生选择不同容量的易拉罐,通过数据计算或测量(见表5),得到至少预留液体容量的10%比较合理.

表5 不同容量的易拉罐的相关数据
因此,模型优化为
对于问题3),学生通过查询文献资料,获知现在国际上最先进的制作工艺的铝材厚度为0.254mm.
将数据代入优化后模型可得
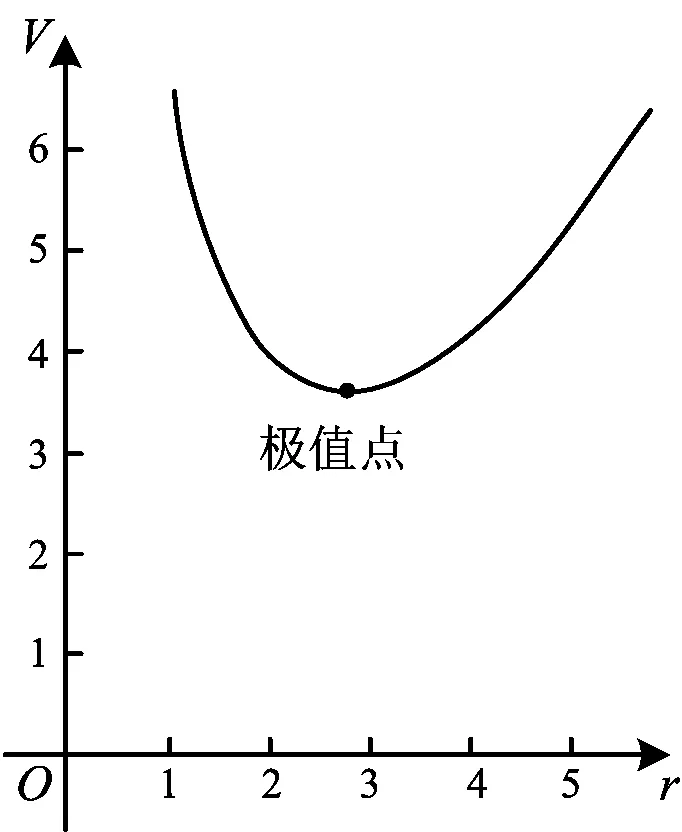
图4
利用GeoGebra软件绘制函数图象(如图4),获得极值点的横坐标r≈2.74.
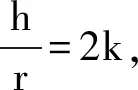
教学说明学生课后进一步研究学习,逐渐产生富有创造性的想法,并形成独创性的项目成果.不仅有对于黄金比在生活中的运用的研究报告,还有对于模型的迁移运用,这些创造性成果不仅促进了学生对项目的深度理解,还丰富了项目学习的评价方式.
3 若干反思
研究表明数学项目学习对于学生数学知识的学习以及非智力层面均有积极意义,但对于课堂教学以及教师自身都提出了一定的挑战,从而引发了相关思考.
3.1 关于项目学习与传统课堂教学关系的思考
数学项目学习是以真实情境为背景、以项目任务来推动学习,数学知识的学习贯穿其中,即前者是“明线”,后者是“暗线”.研究表明,它为学生的思考与探究提供了学习环境,“做中学”更能凸显数学与生活的联系,从而加深知识的理解,发展核心素养.但是数学知识之间是具有内在联系的,而非项目学习中相对零散的数学知识.从核心素养角度来看,模型观念、数据观念、应用意识、创新意识的确在项目学习中能够得到较好的发展,但是抽象能力、运算能力、几何直观、推理能力这类高层次学科素养难以适应这种活泼的教学形式,日常授课更需要传统的课堂教学.因此,项目学习不是对传统课堂教学的一种颠覆,而是一种很好的补充.
3.2 关于项目学习中教师自身的思考
项目学习对教师提出了更高的要求,在传统课堂中教师更多的是知识的传授者,而在项目学习中教师还是项目的设计者和学生研究的促进者、合作者.由于数学项目学习往往是以跨学科的形式呈现,因此需要教师具有更多的知识储备与更高的科研能力.项目学习的设计先要挑选真实情境下合适的主题,并以核心素养为导向设计教学目标,再基于学情设计具有一定开放性、指向不同水平层次的驱动性问题,结合驱动问题与教学目标设计师生协作的教学活动,最后还需要设计“全程式”的评价体系.面对如此巨大的挑战,教师要提升学习能力与合作意识,一方面,积极参加各类数学项目学习的培训,充分利用各种资源,提升理论基础与实践经验;另一方面,加强学科间教师交流,集团队的力量开发高质量的项目学习课程,从而真正通过项目学习发展核心素养.

