在“微专题教学”中追求整体,力求深入
——对一道高考题的教学设计与思考
董昊雷
(宁波市镇海中学,浙江 宁波 315200)
数列是一种特殊的函数,却又有别于常规函数,它能培养学生的数学抽象、数学运算、逻辑推理等核心素养.数列放缩问题是高考中的热点问题之一,也是教学中的难点问题之一.在解决此类问题的过程中,学生往往会遇到“不知道往哪个方向变形,怎么变形,变形完后又该如何处理”等问题.在教学实施的过程中,教师不能进行低层次的记忆加训练的模式,而是要让学生有一个整体的认知,要让学生清楚问题背后的本质.
微专题教学往往具有“因微而准、因微而整、因微而深”的特点.教师在问题设计的过程中要对学生的认知有一个准确的把握,让教学变得更精准;在提炼模型的过程中要对问题有一个整体的认识,让思维变得更完整;在挖掘本质的过程中要对问题有一个深刻的认识,让学习变得更深入.
本文摒弃了“典例—练习—变式”的教学模式,尝试了一种“解一题,懂一法,会一类,通一片”的新微专题教学模式,即通过对一个问题的不断研究,提炼出问题解决的一种方法,从而形成解决一类问题的基本模型,在进一步挖掘此类问题本质的过程中,形成解题教学的一般路径.笔者用思维导图的形式归纳了研究问题的基本思路(如图1).

图1
上述研究问题的路径就是按照“从哪里来—为什么—怎么做—是什么—到哪里去”的思路展开的.“从哪里来”指的是要有一双发现问题的眼睛,能在具体的问题和情境中找到研究的对象,即发现问题和提出问题;“为什么”指的是为什么要这么操作,即提炼解题背后的逻辑;“怎么做”指的是从背后的逻辑归纳出解决问题的基本模型,即抽象和概括模型;“是什么”指的是对基本模型进行更深入的挖掘使其有更一般的应用,即挖掘问题的本质;“到哪里去”指的是这样的问题还能在哪里应用,即模型的应用和提升.
根据以上分析,本文以2021年浙江省数学高考试题第10题为例来研究一类“类等差数列”的放缩问题.
1 教学过程
1.1 从哪里来:发现和提出问题

( )


(2021年浙江省数学高考试题第10题)
参考答案给出了如下解法:

an>0.
由
可得数列{an}单调递减,则
0 (1) 从而 (2) 故 不等式的左、右两边开平方,并整理可得 (3) 根据累加法,可得 (4) 当且仅当n=1时取等号.从而 于是 (5) 根据累乘法,可得 (6) 当且仅当n=1时取等号.因此 即 故选A. 问题1你能独立解决此问题吗? 追问1如果不能,请你结合答案说说哪些步骤是你无法理解的?你认为最关键的一步是什么? 师生活动教师让学生尝试独立解决问题,在解题的过程中寻找自己遇到的难点.接着让学生细读答案并与自己的解题过程相比较,然后整理出自我认知上的难点,此时教师需要将学生的问题进行整理和分类.如上所示,将每一个步骤标记为(1)~(6),学生可能遇到如下的难点:第(2)步为什么要取倒数变形?第(4)步与第(6)步的累加、累乘是怎么想到的?为什么要将第(4)步所得结果代入第(5)步?此时教师通过提问“你认为最关键的一步是什么”将学生的视角聚焦在本节课的核心问题上来,即第(2)步取倒数变形. 设计意图首先,研究的问题要具有“可行性、针对性”,即既要符合学生的最近发展区,又要有一定的研究价值.2021年的这道高考题就是一个很好的素材,它不仅符合以上特点,还能激发学生研究的兴趣.其次,问题1不仅能让学生快速入题,还能让学生在阅读答案的过程中主动地去发现问题,与此同时学生的思维障碍又能作为教师开展教学的出发点.为了帮助学生突破这些难点,教师需要提炼出如下的研究问题的框架:“为什么、是什么、怎么做”,即参考答案为什么会这么操作?这道题目的本质是什么?这类问题该怎么做? 问题2第(2)步为什么要取倒数变形,第(3)步中的式子具有什么特征? 追问2在我们之前的学习中有遇到过类似的数列吗? 追问3你能解释将第(4)步的结果代入第(5)步的原因吗? 设计意图笔者设计问题2的目的不仅是让学生得到“类等差数列”模型,还要让他们理解如何抽象出这个模型.追问2的目的是想让学生将未知的问题与已知的内容产生联系,让知识更有联系性,方法更有系统性,思想更有整体性.追问3是对问题2的再认识,目的是将对问题2的理解应用到追问3的解释中去,对思维进行补充,对认知进行深化.“类等差数列”除了让学生能抽象地看问题外,还能帮助学生对这些步骤有一个更完整的认知,为后续得到解题模型做铺垫.这样的类比与学习能让学生体会知识的应用与迁移,发展学生的数学抽象、逻辑推理等核心素养. 问题3能否归纳出解题的一般步骤? 图2 即 累加可得 求和可得 设计意图问题3的目的不单是要让学生知道如何解这道高考题,更是要让学生形成一般化的解题步骤和模型化的思维.具体来看,每一步的过程都是在运用“类等差数列”“类等比数列”的模型,而每一次操作的目的是让dn或qn的范围变小,从而限制an的范围.此题用模型化的观点看问题是突破难点的关键.当学生知道其背后的逻辑和模型化的操作后,就不会觉得这是优秀学生才能解出的问题.用思维导图将步骤显性化的目的是让学生将研究的思路用于其他问题并能进行有逻辑地表达和交流. 例1中对递推关系的变形有很多: 那么为何要选择第1)种呢?高等数学中的斯托尔茨定理(以下定理1和定理2)可以解释这个原因. (其中L可为有限数,+∞,-∞,但不可为∞). (其中L可为有限数,+∞,-∞,但不可为∞). 斯托尔茨定理可以用于数列阶的估计.回到例1,将递推关系变形为 从而 解得 即 设计意图在教学中,我们发现递推关系的变形有很多种,因此,如何选择就显得至关重要.代数的变形并不是凭经验和记忆,而是有它的理论依据.问题4的目的是希望通过进一步的研究对题目有一个更深入的认识,同时也可以让学有余力的学生通过挖掘问题的本质得到更高阶的知识——斯托尔茨定理.这个定理告诉我们该选择哪一种变形方式,该朝着哪个方向变形.同时,该定理从较高的层次帮学生厘清了放缩的逻辑,构建了整体性的认知.另外,学生能将该问题的研究类比到其他问题的研究中去,当遇到具有挑战性的问题时尝试挖掘问题的本质,用更高的观点看问题. (2015年浙江省数学高考理科试题第20题) 问题5学了本节课的内容后,你能估计例2中的数列{an}与哪个数列同阶吗? 即 设计意图问题5的目的是让学生通过运用所学知识对本节课的理解有一个巩固和提升.对比例1与例2,可以发现其中的解题方法和研究思路是一致的.因此,这两道高考题不仅有助于学生整理思路,还能帮助学生拓展思维.通过这两道高考题,学生可以发现“类等差数列”的形式虽然有很多,但本质都是用斯托尔茨定理找出其中隐含的“类等差数列”,通过放缩限制an的范围.同时这两道高考题都能作为较好的载体帮助学生体会其中隐含的思想方法.另外,在解题的过程中,学生不仅能梳理整节课的思路,将解题步骤进行巩固和优化,还能在分析问题、研究问题、解决问题的过程中发展数学核心素养. 微专题教学应具有“因微而准、因微而整、因微而深”的特点. 1)因微而准.微专题教学要能精准定位教学目标,应该让学生从“学会”走向“会学”.因此,教师对学情的把握要到位,对例题的选择要精准.在教学中,教师要做到“可行性、针对性”.“可行性”指的是问题的选择要符合学生的最近发展区;“针对性”指的是教学的开展要围绕学习的难点和痛点进行.至于例题的选择并不是越多越好,关键是要将问题研究清楚,让学生有所收获. 2)因微而整.教师对“问题的发现、问题的剖析、模型的获得”要有一个清晰的脉络,问题的引导要做到环环相扣,教学环节的设计要做到层层深入.在教学中,既要做到“小整体”也要做到“大整体”.“小整体”指的是能对解题的步骤进行概括形成一般方法;“大整体”指的是能通过一道题的学习获得解决一类问题的方法,形成研究问题的一般路径. 3)因微而深.这里的“深”首先指的是对核心问题的研究要深入,即不仅能挖掘问题的本质,还能将问题进行合理的应用和推广;其次指的是在探索问题的过程中得到解决问题的方法,形成研究问题的思想. 作为教师,要让学生在类比方法和推广思路的过程中获得分析问题、研究问题、解决问题的能力,提高实践与应用的能力,发展数学核心素养,真正达到“解一题,懂一法,会一类,通一片”的目的.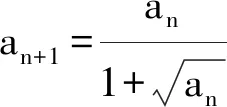

1.2 为什么:剖析背后的原因
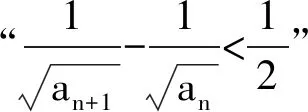
1.3 怎么做:探寻解题的模型


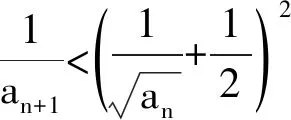

1.4 是什么:挖掘问题的本质
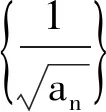



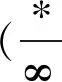


1.5 到哪里去:提升问题的认识
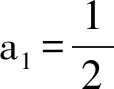


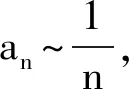

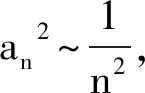
2 教学反思

