一题一课:指向学生思维生长

戴承惠

(舟山市第一初级中学,浙江 舟山 316000)

1 问题提出

在日常数学教学中,部分教师侧重于知识技能的教学,在教学内容上“选题不够灵活,缺乏层次感”,在教学方式上“一讲到底”,忽略学生在学习中的主体地位,造成学生学习负担过重,忽视学生在学习中的数学思考和思维方式的形成,导致学生的学习缺乏迁移能力,知识难以结构化,缺少系统思维;大部分学生对于知识只是被动地接受,没有经过思维的加工,陷入“一学就会,一用就错,一放就忘”的困境,思维模式单一固化,缺乏提出猜想与质疑的动力,很难主动提出问题.

因此,笔者提出“一题一课”教学设计框架(如图1).从知识层面看,立足章节、体系的整体认知;从学习方法层面看,更多体现学生的自主性,让学生学会学习、学会思考,促进学习策略与学习方法的获取.

图1

2 “一题一课”的教学价值

2.1 低起点,发展思维的灵活性

以“一题”为抓手,教师从一个初始问题出发,把握好学生知识生成的最近发展区,找准思维生长的起点,选好生长路径,从不同角度、不同方面帮助学生不断生长新的数学知识、方法、经验,激发学生思维的灵活性.

2.2 重提问,发展思维的创造性

问题是思维的起点.教师应创设开放问题,构建问题场域,激活学生的数学思维,引导学生在学习中提出不同的观点;要及时对学生如何提问、从哪些角度提问进行指导,让学生敢提问、会提问;及时梳理学生的问题,提炼核心问题,指向学生思维生长的刺激点,让学生在分享问题、解决问题的过程中自然架起一座思维的桥.

2.3 高立意,发展思维的深刻性

教师要整体把握教学内容,帮助学生构建数学知识体系的横向、纵向联系,找准思维生长的发散点,促进学习的迁移,让学生在一开始学习时就能“见木见林”,使知识呈现出生命态,唤醒并点燃学生学习的目的性和主动性,激活学习的内驱力,学生的思维才有深度,对知识的理解也会更加深刻.

3 “一题一课”的教学策略

3.1 逆向寻源,加快思维的速度

基于教材例、习题,借助归纳、类比、迁移等思维方式,实现基础知识、基本技能、基本方法、基本思想上的关联,形成一条思维链,运用问题链引发学生系统思考,达到“学一题,会一类,通一片”的效果,培养学生养成学习品质、锻炼创新思维和逆向思维的能力.

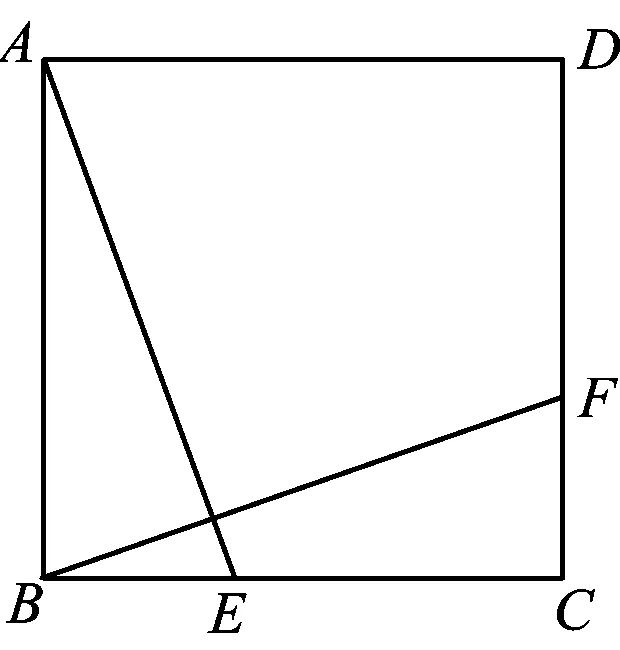
图2

案例1浙教版《义务教育教科书·数学》(八年级下册)第5.3节“正方形”(第2课时)作业题A组第4题.

问题1如图2,在正方形ABCD中,E,F分别是BC,CD上的点,AE⊥BF.求证:AE=BF.

变式1如图3,在正方形ABCD中,若HF=ME,试问:ME⊥HF是否成立?

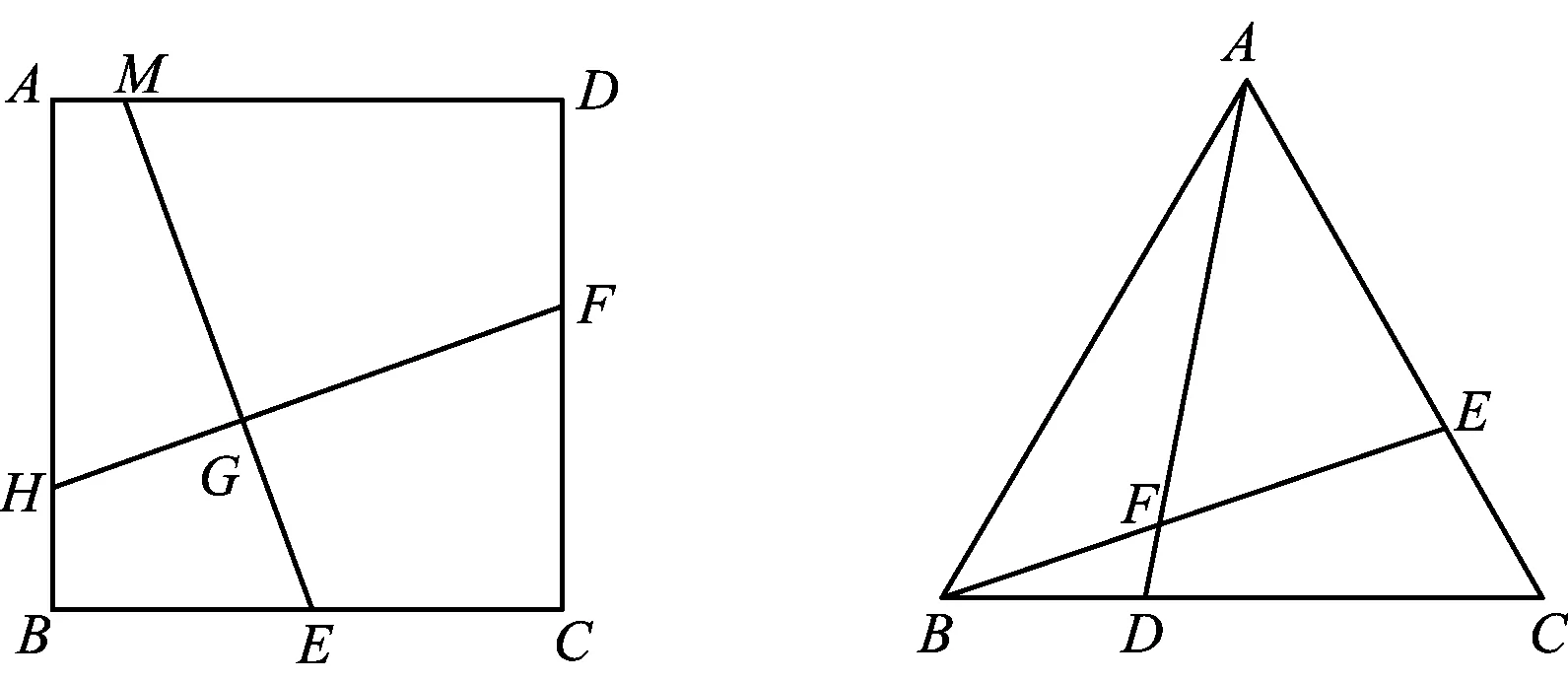
图3 图4

迁移如图4,在正△ABC中,D,E分别是BC,AC上的点,且∠AFB=120°.那么AD和BE相等吗?请你尝试模仿编一道题目.

教学解读精选“一题”,生长新知识,指向数学的本质,让逆向思维在“问题链”中绽放光彩.如图5,ME,EN关于EY轴对称,则EM=EN=HF;由静到动对EN进行平移(如图6),使EN=ZW,由浅入深,这样的ZW有无数条.数学问题解决的本质是迁移,把正方形中的基本结论、基本思路和基本方法,迁移到正三角形中[1],逐步培养学生自主探究和类比的能力与意识,通过“学结构”学会“用结构”生长“新结构”,促进了知识的再创造,以知识迁移加快思维速度.

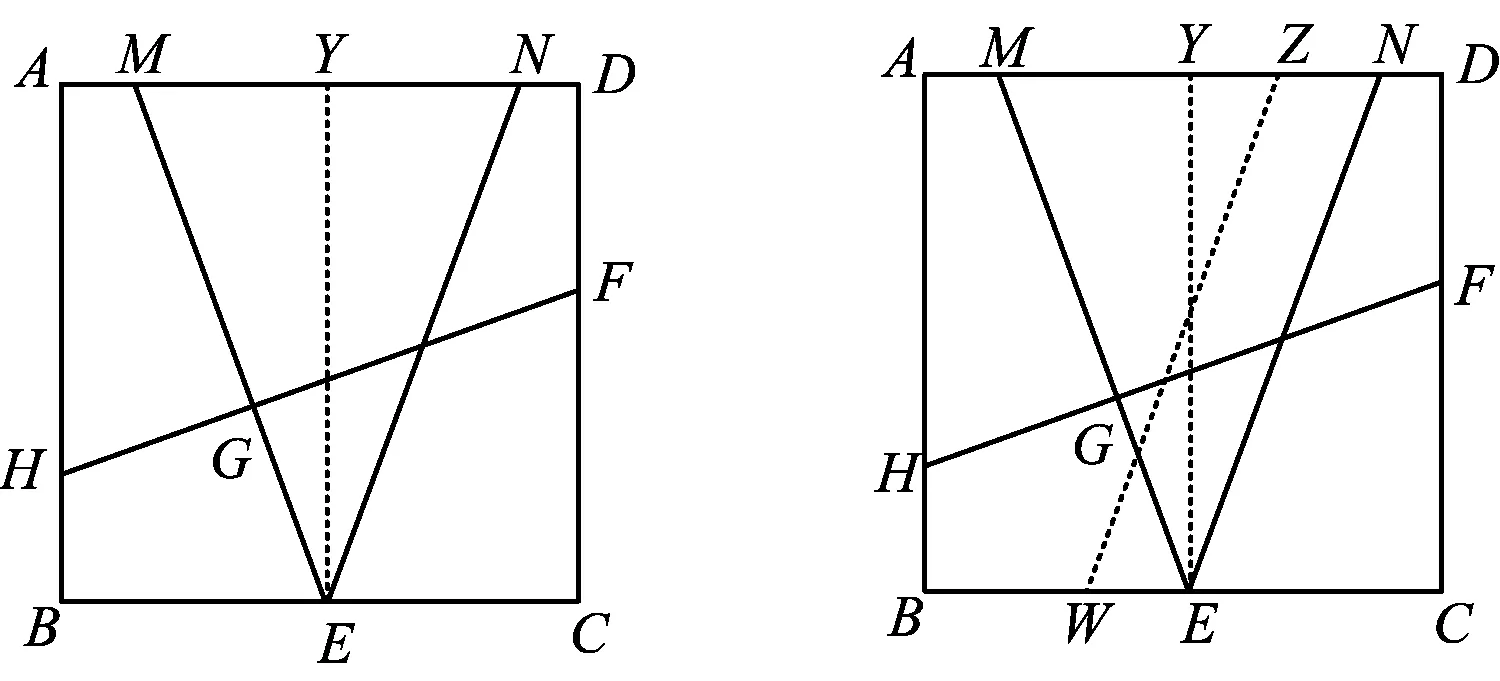
图5 图6

3.2 图形“加减”,挖掘思维的深度

在数学教学中,选取典型习题,一题(图)贯之,对题目的条件进行添加、减少、类比及图形变化实现多维度变式,衍生问题,层层推进,把核心的知识技能、思想方法等融入其中,挖掘出更多、更有价值的数学问题,最终达到“举一反三”的教学目的.

案例2“一道经典中考题”的专题复习课.

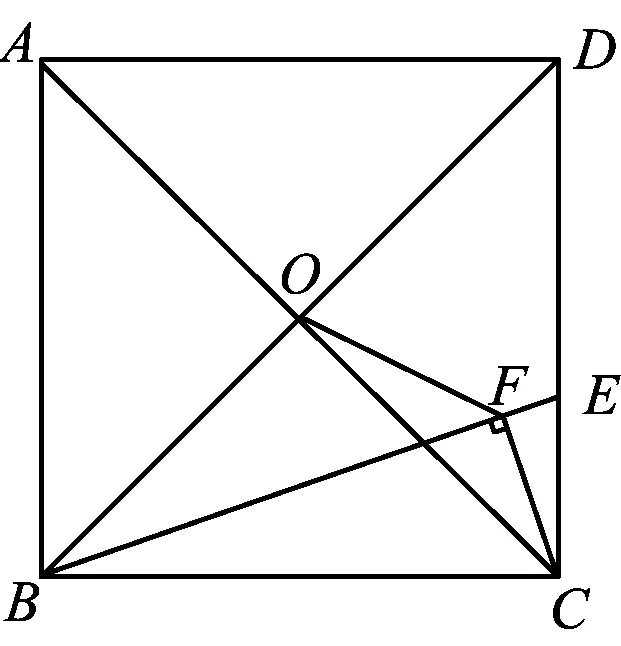
图7

问题2如图7,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在CD上,且DE=2CE,过点C作CF⊥BE,垂足为点F,联结OF,则OF的长为______.

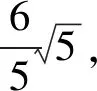
评注以正方形为背景,求OF的长度,引导学生深度剖析图形结构,鼓励学生独立思考,一题多解,解法优化,形成自然简洁的解题策略,着力考查学生的几何直观、推理能力、运算能力、应用意识等数学核心素养,为日常教学起到了良好的导向作用.

变式2(运动视角)如图8,正方形ABCD的边长为6,点O是对角线AC,BD的交点,点E在DC的延长线上,且DE=3CE,过点C作CF⊥BE,垂足为点F,联结OF,则OF的长为______.

图8 图9

变式3(结构视角)如图9,在菱形ABCD中,BD=2AC,E为边CD上一点,CF⊥BE于点F,猜想并证明OF,CF,BF的数量关系.

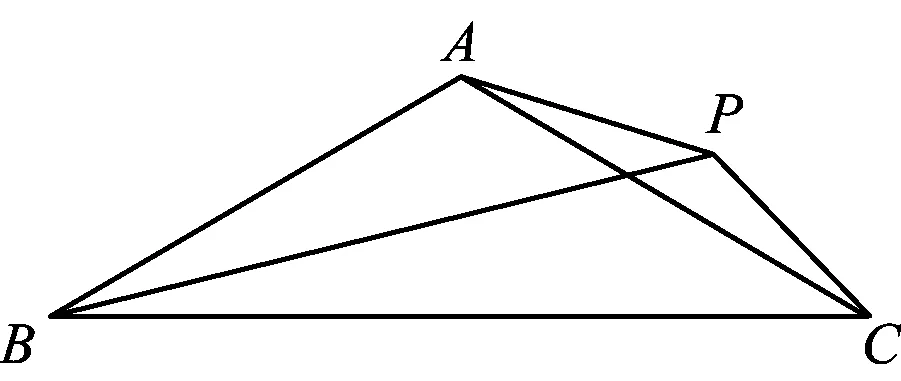
图10

变式4(有“型”无“形”)如图10,在△ABC中,AB=AC,点P是三角形右外一点,且∠APB=∠ACB,若∠BAC=120°,猜想并证明PA,PB,PC的数量关系．

教学解读问题2注重感悟方法,变式2和变式3分别从运动和结构视角帮助学生内化方法.用心体会“一题”的价值,设计具有挑战性、延伸性的问题,追求“一题多能”,勇敢大胆地摒弃“题海战术”,注重解题后的反思,加深学生对通性、通法的认识,避免碎片化解题,造成“只见树木不见森林”的学习误区.对同一题目条件进行剖析,从不同视角分析探索,内化解题方法,追求解法自然,基于图形结构类比生长,从有“型”到无“形”,实现“一题”生长“多题”,“多题”归一成“一课”,不断促进学生思维向更深更远的地方生长.

3.3 整体设计,提升思维的力度

在单元复习课上,要把复习内容置于整体知识体系中,以开放性的问题统领知识主线的建构,用核心问题引领学生思考,促进学生对知识体系的融会贯通,帮助学生将知识结构化、系统化,让认知思维走向高阶.

案例3浙教版《义务教育教科书·数学》(七年级下册)第5章“分式”复习课的设计思考.

活动1给出诸如5,x,x+2,x-2,x2-4,x2-2x等代数式,写出尽可能多的分式,并把结果化成最简分式.

活动2在写出的分式中选择2～3个进行运算,并计算结果.

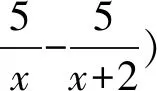
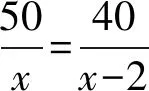
教学解读活动1从开放问题引入,复习分式的基本概念、基本性质,为分式的运算提供素材.活动2引导学生自主建构分式基本运算,着重复习异分母分式相加减、分式乘除法的基本步骤以及运算顺序,进一步梳理与内化学生的认知结构.活动3和活动4通过已经列好的分式、分式方程,引导学生用逆向思维构建真实的情境,可以深化学生对所学知识的理解,引导学生在“说数学”中表达自己的思考,逐步增强学生的数学应用意识,积淀个性化的经验,促进学生数学核心素养的形成.整个过程,4个环节,环环相扣,始终凸显学生的学习和思考,学生通过解决问题形成了整章知识的框架体系,促进数学知识结构不断优化,在丰富数学应用意识的同时加强思维力度.

3.4 一题多变,拓宽思维的广度

从一个问题出发,隐去问题的结论,引导学生对问题的结论进行多角度、多层次地探究,摆脱固定模式的变式.由于思维的差异性,学生自主探究会更具层次性;学生自发、自主地提出问题时,更能建立认知结构的“承重墙”,沟通不同内容之间的内在联系,打通“隔断墙”,形成“一览众山小”的感觉,把握数学本质.

案例4浙教版《义务教育教科书·数学》(七年级下册)因式分解复习.

问题3请在下面的括号内添上一个整式,并对补全后的整式进行因式分解,你有几种方法?请说说你的做法?

9a2-( )=______.

教学解读巧设“一题”,贴近学生的认知水平,在开放性问题中打开学生思维,在交流探讨中完善知识结构.问题3看似只涉及一个平方差公式,实际上内容丰富、综合性强、方法灵活多样[2],考查了基础知识提取公因式、公式法(平方差公式、完全平方公式).在此过程中,教师对学生及时进行学法指导,激发一部分学生的探索欲望,打开思路,从关注知识到关注思想方法,从一题多解到多题归一;提炼数学思想,着力挖掘“简约”背后的“深刻”.同时,教师引导学生完成对因式分解的知识和方法的整合,让学生的学习有思维含量,逐步走向理性的深刻分析,将学生以往的数学经验和积累变为思维生长的养分,从而发展学生思维的广度.

4 结束语

以“一题”为载体组织教学,厘清问题蕴含的生长功能,不断添枝加叶,使得题尽其能,聚拢于各年级教材中的相关基础知识,增进关联,凝聚成一个有机的整体系统,重构知识体系;坚持“以生为本”,并自主探索求新,激发了学生思考和学习的积极性;引导学生提出“精准”问题,共同解决问题,在思维的碰撞中促进知识之间的融合、修正、再生、发展并形成新知.长此以往,这样的数学教学过程,学生的学习主动性就会增强,发现问题和提出问题的意识得到激活,思维能力才能真正得到提升.