运动视角寻关联 定形变换显路径——从一道几何题的解法谈起

郭源源, 缪 娟

(1.南京市雨花台区教师发展中心,江苏 南京 210022;2.南京市竹山中学,江苏 南京 210000)

数学教师的专业基本功不仅包括教学设计能力、课堂教学能力,还应包括较强的解题能力和命题研究能力．一道好的几何试题,往往具有图形优美、结构清晰、贴合思维、解法多样、可变式可拓展等特点,它既是学生感知条件联想、引发深度思考、提升思维能力的好题目,也是教师进行习题研究、探寻主题拓展、提升专业素养的好素材．下面笔者以江苏省南京市雨花台区中考复习中的一道几何题为例,对其结构、解法和拓展进行探究,供同行研究参考．

1 试题呈现

图1

例1如图1,在等边△ABC中,D是BC上一点,将线段DB绕点D顺时针旋转120°得到DE,联结BE,CE,F是CE的中点,联结AF,DF,求证:∠AFD=90°．

2 结构分析

在探寻解题思路之前,应先充分地审题,即弄清主要问题,厘清问题的条件和结论,分析图形的的构造过程,把握图形的特征,明晰题目的结构．

2.1 分析条件

此题的条件部分可分为3组:1)等边△ABC;2)在△DBE中,DB=DE,∠EDB=120°;3)F是CE的中点．

2.2 分析图形

从构图角度分析,点D在边BC上运动,点D一旦确定,旋转后的点E就确定,中点F也随之确定,即∠AFD构成．进一步分析∠AFD为定角,与点D在边BC上的位置无关,而与旋转120°及中点F有着重要的关系,可以将图形“特殊化”思考,即当点D与点B重合时,不难发现F位于BC的中点处,由等边三角形“三线合一”得∠AFD=90°．因此,例1的内部结构必与边BC上的高有着千丝万缕的关系,这也是后续形成解题思路的关键．

2.3 分析结论

由几何直观可猜想结论为∠AFD=90°．因为单一的“直角”能发挥的作用是有限的,所以需要给它找个“家”,即△AFD,分析着眼点从关注直角∠AFD转移到关注Rt△AFD．结合上述“特殊化”的分析,可进一步猜想△AFD为含30°角的直角三角形,形状和“点D与点B重合时的△AFD”相同,从而得到更精准的结论:△AFD绕点A运动且形状保持不变,即进行“定点+定形”的变换．这样看待图形变化的眼光就有了,图形前后“保形”运动的来龙去脉就清楚了,解题思路也随之诞生．

3 解法探究

经上述结论分析,此题的视角从证明“∠AFD=90°”优化为证“△AFD为含30°角的‘定形’直角三角形”．在等边三角形的背景下,这种形状的直角三角形有很多个,而选择其中不同的三角形作为源头,即可产生不同的路径变化,造就不同的“旋转双相似”[1],从而产生不同的路径解法．

思路1以A为定点,绕点A旋转寻图形关联.

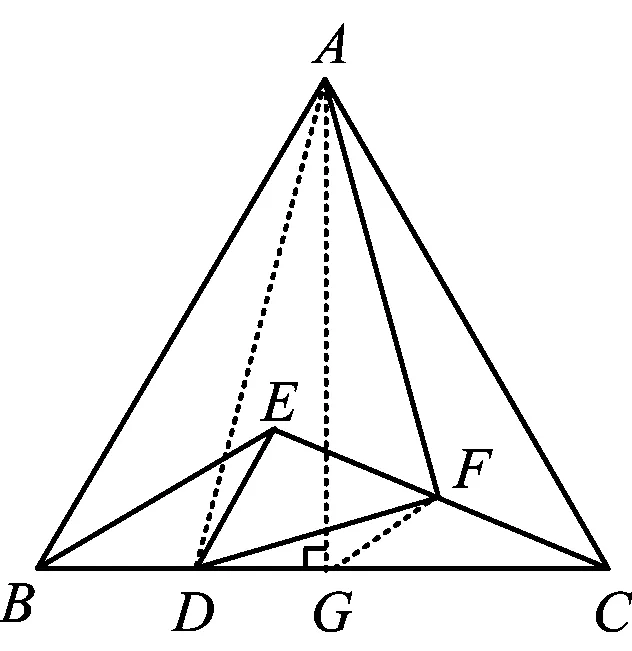
图2

证法1(视为由△AGB旋转相似而来)如图2,过点A作AG⊥BC于点G,联结GF,AD．要证△AFD∽△AGB,根据“旋转双相似”模型,只需证△AFG∽△ADB即可．易知G为BC的中点,由FG为△EBC的中位线,得

FG

从而

∠FGC=∠EBD=30°,

可得

∠AGF=∠ABD=60°．

因为

且

所以

因此

△AFG∽△ADB.

进一步可证△AFD∽△AGB,得

∠AFD=∠AGB=90°．

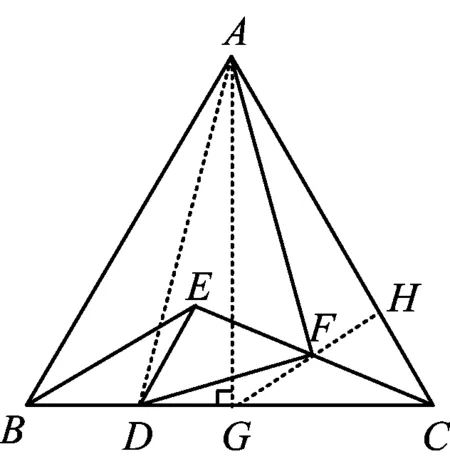
图3

同证法1,可得

从而

因为∠AHF=∠AGD=90°,所以

△AHF∽△AGD,

即可证得∠AFD=90°．

思路2以D为定点,绕点D旋转寻图形关联.

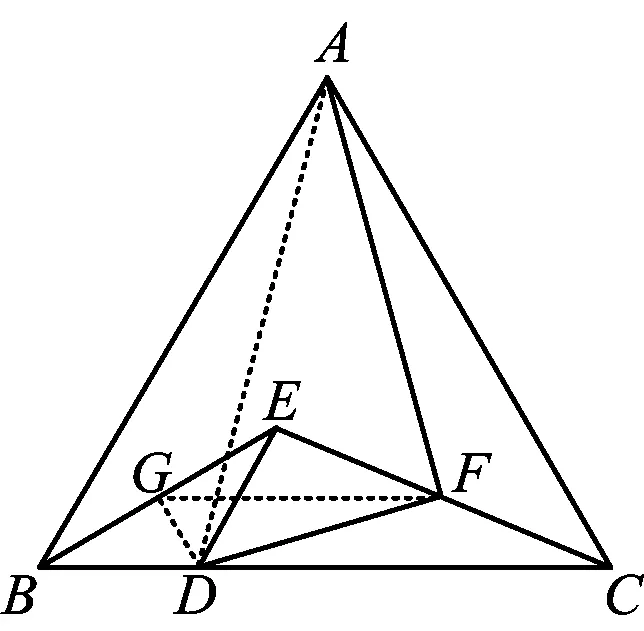
图4

证法3(视为由△BGD旋转相似而来)如图4,取BE的中点G,联结DG,GF,AD．易知DG⊥BE,DG平分∠BDE.同理分析,要证△BGD∽△AFD,只需证△GDF∽△BDA即可．由FG为△EBC的中位线可知

FG

得

∠DGF=∠BDG=60°,

即

∠DGF=∠DBA．

因为

且

所以

从而

△GDF∽△BDA,

即可证得∠AFD=90°．

思路3以F为定点,绕点F旋转寻图形关联.

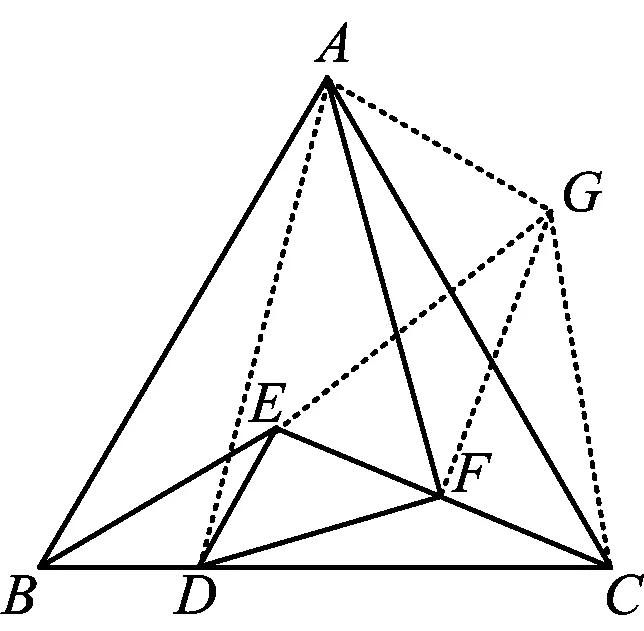
图5

证法4(视为由△GFE旋转相似而来)如图5,以EC为边构造等边△GEC,联结GF,AG,AD．易知GF⊥CE,GF平分∠EGC.同理分析,要证△GFE∽△AFD,只需证△FED∽△FGA即可．由△CBA和△CEG都是等边三角形,可证

△CGA≌△CEB,

从而

AG=BE, ∠AGC=∠BEC.

由∠CGF=∠BED=30°,可得

∠AGF=∠DEF．

因为

且

所以

因此

△FED∽△FGA,

即可证得∠AFD=90°．

评注上述3种思路都是聚焦△AFD,想方设法从已有的图形结构中寻找含30°角的直角三角形与△AFD“配对”,形成“定点+定形”的变换．从而借助运动的眼光,关联这两个形状相同的三角形,映显出图形变化的路径,再通过路径之间量的关系证得相似,即从“聚焦形”到“关联形”,再到“量化形”,这也是“旋转双相似”模型常用的分析策略[2]．

思路4倍长中线,补全图形寻整体关联.

图6

证法5(倍长DF,关联△ABC)如图6,延长DF到点G,使得DF=FG,联结AD,AG,CG．要证△AFD是含30°角的直角三角形,只需证△ADG是等边三角形,再关联等边△ABC,只需证△AGC≌△ADB即可．由EF=CF,DF=FG,易证

CG∥ED,CG=ED,

可得

CG=BD, ∠GCD=∠EDB=120°,

即

∠ACG=∠ABD=60°．

因为AB=AC,所以

△AGC≌△ADB,

即可证得∠AFD=90°．

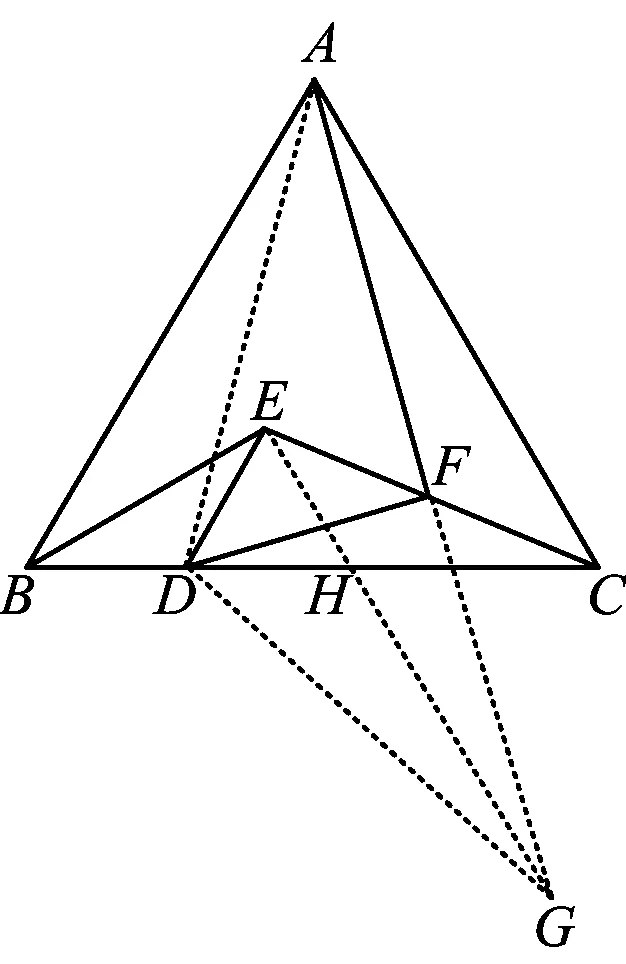
图7

证法6(倍长AF,关联△DBE)如图7,延长AF到点G,使得FG=AF,联结AD,DG,EG．要证△AFD是含30°角的直角三角形,只需证△ADG是含120°角的等腰三角形,再关联△DBE,只需证△DEG≌△DBA即可．由EF=CF,AF=FG,易证

EG∥AC,EG=AC,

可得

EG=AB, ∠EHD=∠ACB=60°．

又由∠EDB=120°,得

∠DEG=60°,

即

∠DEG=∠ABD．

因为DE=DB,所以

△DEG≌△DBA,

即可证得∠AFD=90°．

评注上述思路不再拘泥于△AFD,而是着眼于整体构造．基于中点,通过倍长中线构造能与△ABC或△DBE直接关联的三角形,即“共顶点的等腰三角形”,从而形成“手拉手”全等的思路方法．这是八年级全等章节中非常重要的基本模型,也是解题中对“中点”条件常用的处理策略．

思路5互相补形拼直角,构旋转相似模型.

图8

且∠AFD等于HE与CG的夹角,即∠AFD=90°．

评注△AFD,△DBE分别为等边三角形、含120°角的等腰三角形．这两种形状的三角形本身是关联的,它们恰好是含30°角的直角三角形斜边中线所分割的两个部分.因此,通过补“形”,让这两个部分的三角形达到形状相同的效果,直接形成“定点+定形”的旋转背景,从而看透AF与FD的数量和位置关系,这也是后续将问题“一般化”的拓展研究视角．

4 问题拓展

通过变换构造几何图形,其内在元素的数量和位置关系是非常多的,其变式问题也是无穷无尽的.一般而言,可借助“特殊化”“一般化”“可逆化”等方法将问题变式继续拓展研究．本文限于篇幅,笔者在这里只借助“一般化”,对问题进行拓展．

4.1 位置的一般化

从构图的角度来看,可认为点D的确定带来了后续整个图形的确定,因此可以对点D的位置进行“一般化”．

变式1(D为平面内任意一点)如图9,△ABC是等边三角形,D是平面内任意一点,将线段DB绕点D顺时针旋转120°得到DE,联结DE,BE,F是CE中点,联结AF,DF,求证:∠AFD=90°．

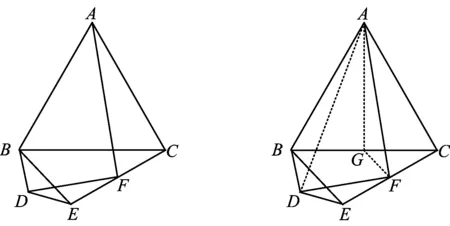
图9 图10

简证1(同证法1～4的思路)如图10,过点A作AG⊥BC于点G,联结GF,AD．要证△AFD∽△AGB,只需证△AFG∽△ADB即可．由FG是△BEC的中位线可知∠CGF=∠CBE,进一步可得

∠AGF=∠ABD．

同证法1得

因此

△AFG∽△ADB,

即可证得∠AFD=90°．

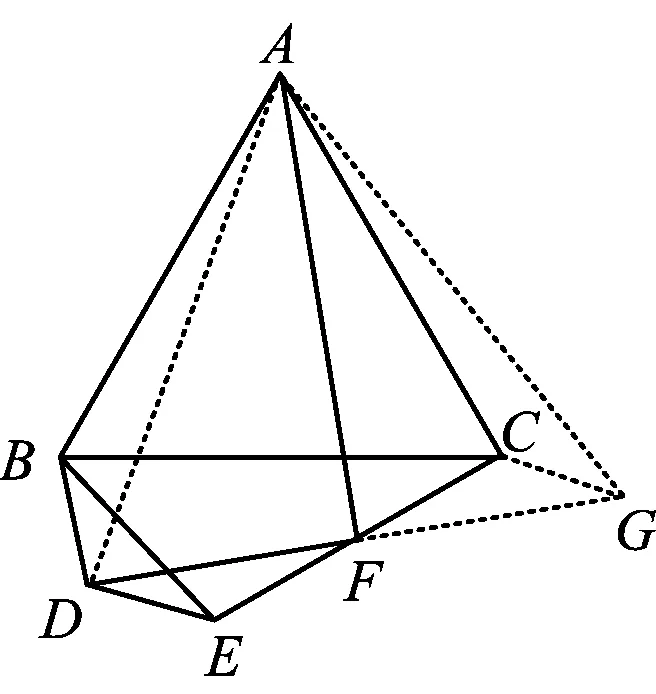
图11

简证2(同证法5～6的思路)如图11,延长DF到点G,使得DF=FG,联结AD,AG,CG．由EF=CF,DF=FG,易证

CG∥ED,CG=ED,

可得

CG=BD, ∠FCG=∠FED．

又由四边形BDEC的内角和为360°,知

∠DBC+∠DEC+∠BCE=240°,

即

∠DBC+∠BCG=240°,

从而

∠ACG=∠ABD.

因为AB=AC,所以

△AGC≌△ADB,

即可证得∠AFD=90°．

评注虽然点D的位置变了,但条件中所有涉及的关系都没有变,因此整个图形的关系结构仍然是存在的,例1中的所有证法思路仍然是成立的,其他证法同理可得．

4.2 数量的一般化

位置“一般化”后,继续思考数量能否“一般化”呢?例1中的等边三角形与含120°角的等腰三角形有着密切的关联．若变成顶角为α的等腰三角形与顶角为(180°-α)的等腰三角形,还会有这样的结论吗?

变式2(△ABC与△DBE为顶角互补的等腰三角形)如图9,在△ABC中,AB=AC,∠BAC=α,D是平面内任意一点,将线段DB绕点D顺时针旋转(180°-α)得到DE,联结DE,BE,F是CE中点,联结AF,DF,求证:∠AFD=90°．

图12

思路1该题仍然可以借助变式1的思路．如图12,过点A作AG⊥BC于点G,联结GF,AD．由∠BAC=α,∠BDE=180°-α,易证得

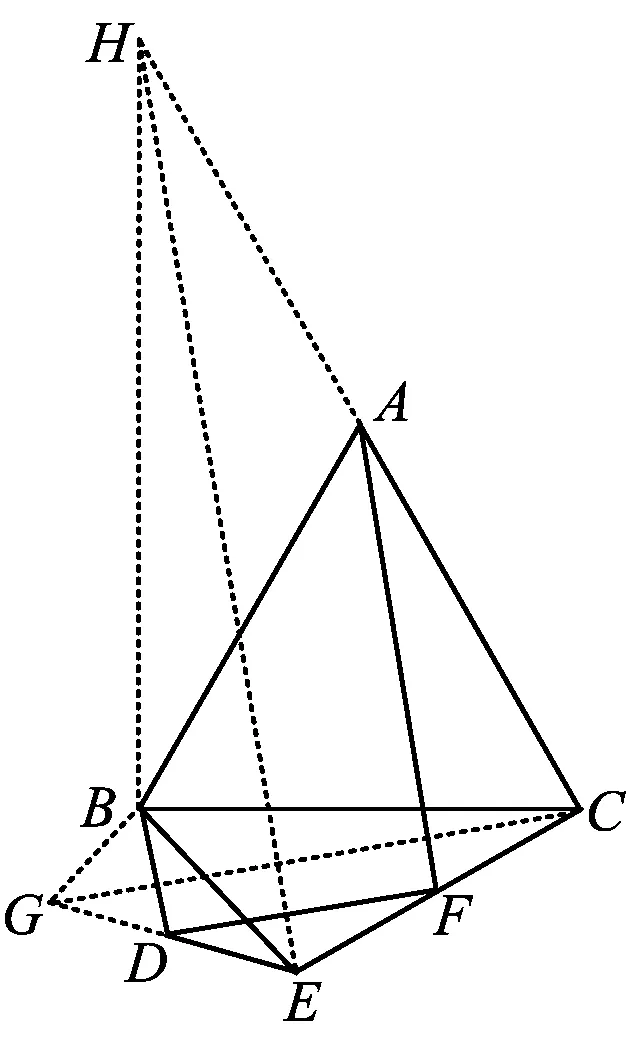
图13

△HBC∽△EBG,

进一步可证

△HBE∽△CBG．

后续与上述证法7的思路如出一辙,证明略．

评注虽然位置与数量关系都改变了,但整个图形的结构关系依然不变,原题中的所有解法思路仍然适用．通过拓展研究,得到了更“一般化”的结论:两个顶角互补的等腰三角形,若其中一对底角的顶点重合,则另一对底角顶点连线的中点与各顶角顶点连线形成的夹角为直角,可以简称为“脚踢脚”模型．它的各类解法是“旋转变换”中路径问题的另一种呈现,也是“中点”联想构图的典型方式,同时还是“手拉手”旋转相似的局部关联体现．因此,例1是研究几何图形、挖掘内部关系结构的经典素材．

5 写在最后

苏霍姆林斯基曾说过,教师所掌握的知识深度,应当比他课堂上讲的知识多百倍,以便在课堂上能灵活自如地玩转教学,能游刃有余地指导学生的思维发展．这说明了教师不断学习、不断研究的重要性．数学是思维的科学,思维又是隐性的,需要好的主题和素材作为思维的载体,引发学生思考的热情,而这种热情正是数学教学要追求的“一股劲”．因此,作为数学老师,平时更应该养成勤思考、善发现、爱钻研、能积累的品质.只有教师不断地去研究,才能让模型结构化、脉络化,也才能发现和提出更多新的问题．只有教师爱思考,学生才会爱思考,同时思考过程中思维的发展也正是数学的魅力所在[3]．例如,本文中的顶角互补的等腰模型,这是“手拉手”全等和旋转相似问题之后的又一次思考,图形内部蕴藏的关系更密切,可变式的方向也更多．若对变式2继续进行“一般化”探究,将△ABC和△DBE“两腰相等”的条件弱化成“两边对应成比例且夹角互补”,则∠AFD还会是直角吗?它的大小由哪些元素来决定?读者可继续思考研究．

“穷尽所有可能与变式”是研究同一类问题的常用方式.钻透每一种变式,从“定”与“变”的视角看问题,借助图形变换揭示问题内部的结构和体系,从而感悟问题内每个元素之间的联系．在这样的研究方式下,题目将从一题走向无限,从封闭走向开放,充满着灵气和生命力．因此,笔者认为,教师对问题的认知,不能仅拘泥于问题本身,还需要养成变式、穷尽、拓展的习惯,这样不仅有助于提高自身对问题的认识,还有助于提升自己的解题能力和命题水平,同时也有助于提升教师的深度教学和学生的深度学习．