关注几何通性 实现教法迁移 落实整体教学
——以“圆的基本性质”为例
邓莉莉
(杭州市临平区树兰实验学校,浙江 杭州 311100)
1 教学现象
笔者认为教材中几何内容的编排有待改进,一线教师应从横纵双向对相关内容进行必要调整,让教学内容更符合学生的认知规律,更有助于学生理解,从而实现“四基”,发展“四能”.借助“螺旋式”教学方式,实现教学内容结构化、知识系统化,拓展和加深教学内容,真正落实数学核心素养.点动成线、线动成面、面动成体,教师应引导学生从直观的角度观察现实生活中的数学问题,将静态问题变成动态问题,让数学动起来,感受数学的无穷魅力.笔者将初中阶段几何问题中的点线问题整理成如图1~4所示的4种类型,以实现几何的基础教学.

图2
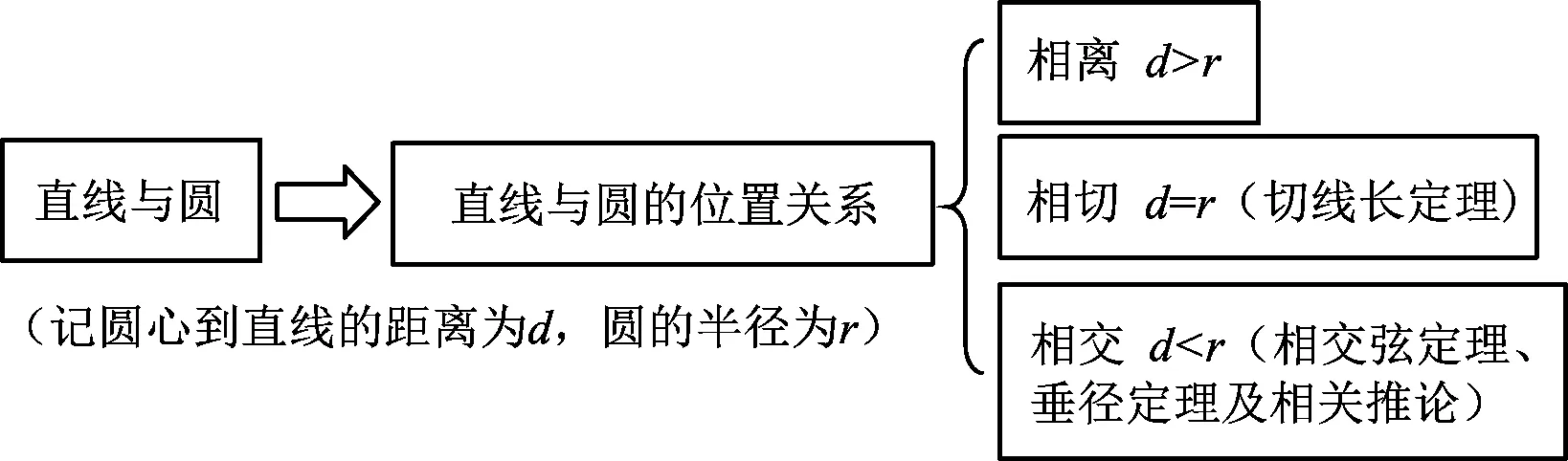
图3
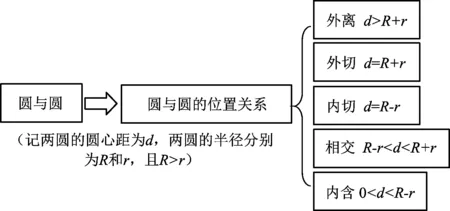
图4

图1
以下拟从寻求几何通性、实现教法迁移、最后落实单元整体教学的思路出发,以浙教版《义务教育教科书·数学》(九年级上册)第三章“圆的基本性质”为例谈谈单元整体教学的设计和实践.
2 教学相关内容的解读
点与线都是原始概念,教材中没有具体的定义.这正是几何教学的难点所在,也是几何教学的一个突破点.教师如何定义点与线,才能更好地诠释几何图形之间的关联,实现几何教学整体化、系统化?如何“开头”是一线教师应该思考的问题.点是最简单的形状,是几何图形最基本的组成部分,它在空间中只是作为一个零维对象.在初中阶段的平面几何中,点在平面中只有位置而没有大小.在最初的定义中,点是没有部分的东西;而在二维欧氏空间中,把一个点表示为一组有序数对,因此,在笛卡尔坐标系中,任意一点都能用一组有序数对表示,以确定其在平面上的准确位置.
在现阶段相关资料中,有关线的概念大致可分为以下3类:
观念1线是由无数个点集合成的图形.
这种解释很抽象,在实际教学中学生无法理解,特别是“点集合成”中的“集合”二字过于抽象.对初中生而言,这样的定义没有给出具体的图形,没有抽象出示意图,不符合学生学情和数学概念教学,有些脱离实际.
观念2线——无宽度有长度.
这种定义非常片面,只指出线在数学领域无粗细之分,与现实领域中的“线”有一定区别,但没有形成具体图形,没有形成几何直观,不利于线的概念教学.
观念3线是由一个点运动产生的图形.
笔者认为这样的定义能更好地诠释“点动成线”,结合初中阶段的平移、旋转变换来描绘点的运动过程,更加直观地阐述线的定义.一个点沿着某一个方向平移一定距离所形成的运动轨迹称为线段,如图5所示即为线段AB或线段BA,移动的距离为线段的长度.

图5
从运动的角度出发,能够更好地诠释圆的形成.点的方向、位置都不断发生变化,体现圆弧不仅有长度还有角度.圆的旋转不变性是圆特有的性质.因此,要从对称性、旋转不变性两个方面出发探究圆中弦、弧、圆心角与圆周角等要素之间的关联,这也是圆相关知识的重点与难点.
3 学情的剖析
基于小学阶段对圆及周长、面积公式的认识,结合几何知识的相关学习经验,笔者以类比的方式整体设计教学方案,让学生感知知识的整体性和系统性,把零散的知识集中化,发现其异同点,挖掘更深层次学习的突破口,进一步拓宽和加深课程内容,采用“螺旋式”教学的方式,更适应学生发展的需求.
4 教学目标
1)实物、多媒体动态展示点的运动轨迹,类比直线的概念,用数学的眼光直观感受并抽象出圆及其相关概念;
2)通过几何画板软件的演示和实物操作,猜想并证明垂径定理、圆心角定理、圆周角定理,从中经历知识的“发现”“再发现”“从一般到特殊”的探究过程[1];
3)在圆的基础知识的学习过程中,实现“四能”的发展,培养学生质疑问难的批判思维,学会用辩证唯物主义观点观察世界,形成实事求是的科学态度与理性精神,实现学生核心素养的发展.
5 教学过程的设计
5.1 圆及其相关概念
回顾小学阶段圆的相关知识,教师引导学生开展以下探究:
问题1用一根绳子或圆规画圆,说说在画圆的过程中应该注意哪些,结合直线的概念给圆下定义.
设计意图在实践操作中,让学生感知圆的形成过程.圆是由无数个点构成的一条封闭曲线,运动中点的位置和方向都在发生变化,为弧的引入埋下伏笔;点在变中仍有不变量,即任意时刻停下来,动点与圆心之间的距离不变;对圆规而言,无论何时停留,圆规两脚之间的距离始终不变.教师不断引导学生获取圆的概念及相关表示方法.
问题2回顾点与直线的位置关系,点与圆又有哪几种位置关系?
设计意图借助点与直线的位置关系,用类比思想让学生感知圆是线,是一条封闭曲线,并且把平面分成了3个部分.由点与圆心之间的距离与半径的大小关系,来确定点与圆的位置关系,让学生感知圆心的重要性.
问题3圆弧上任取两点所作线段称为弦.固定其中一个点,另一个点在圆上运动的过程中,弦长有何变化?
设计意图利用图形直观,抽象出圆中弧和弦的概念;类比三角形中对边与对角的关系,以实践活动的方式让学生深刻体会弧、弦之间的关系:一弧对一弦,一弦对二弧;再用从一般到特殊的方式,以特殊弦引入圆中弧,归纳说明“直径是圆中最长的弦”后,利用圆的轴对称性引入“半圆”,结合弧与半圆之间的对比,获取“等弧”“优弧”“劣弧”的概念.
问题41)以点O为圆心,可以画多少个圆?这些圆有什么共同特征?
2)以3 cm为半径画圆,这样的圆可以画多少个?这些圆又有什么共同特征?
设计意图以问题串的形式,对圆的不唯一性进行讨论,自然引入“同心圆”“等圆”的概念,让学生感知圆心和半径是确定圆的两个要素:圆心可以确定圆的位置,半径可以确定圆的大小.
问题5已知两点确定一条直线,而圆是曲线,且圆上任意两点无法确定一个圆,那需要几个点才能确定一个圆呢?
设计意图再次强调圆是曲线,而两点只能确定一条直线.让学生从平面中的点出发,类比直线的定义方式,给出确定圆的另一种方法:不在同一直线上的3个点确定一个圆.让学生实践操作并观察,在教师的引导下,利用类比的方式抽象出确定圆的另一种方式,经历发现和探究的过程,让学生对所学知识进行猜想、分析、论证、归纳,感受“四能”才是做数学研究的必备能力.
5.2 过圆心的直线垂直于弦——垂径定理
教师引导学生从圆中两条弦的位置关系出发,结合特殊弦,构建弦与弦所对弧之间的关联并进行探究.
问题6画出圆中两条弦的位置,小组进行讨论并画一画具体有哪些形式?
设计意图结合圆心的位置,让学生自主探究圆中两条弦的位置关系,从一般到特殊,给出各种位置关系:
当AB∥CD时,如图6和图7所示.

图6 图7
当AB与CD相交时,如图8~13所示.

图8 图9

图10 图11

图12 图13
问题7在相交的情况下,哪些图形中两条弦的位置关系比较特殊?哪个图形中的弦比较特殊?在特殊位置和特殊弦下,所截的弧之间又有怎样的数量关系?
设计意图在相交的特殊情况下,借助“一条特殊弦为直径”给出直径垂直弦,引导学生研究问题应该从一般到特殊,再从特殊到一般,以便获取更多相关知识.学生从直径与弦的位置关系、弦、弦所对弧这3个方面出发进行猜想,利用圆的轴对称性和旋转不变性,用“验证+证明”的方式得到垂径定理和弧中点的性质,最后结合命题的相关知识,呈现垂径定理逆定理并进行论证.
问题8在图6和图7中,两条平行弦截得的圆弧有怎样的数量关系?在图13中,两条垂直弦截得的圆弧之间又有怎么样的数量关系?请说明理由.

5.3 圆心角定理
除了上述的平行弦与垂直弦,教师让学生再次观察如图8~11所示的相交的一般情况,引导学生观察相交情况下交点与弧之间的关系,实现知识的外延和扩展,充分调动学生学习的积极性[3].
问题9再次观察图8~11,两弦交点与圆有哪些位置关系?
设计意图教师引导学生考虑当两弦(或者其延长线)相交时交点与圆的位置关系,给出“圆内角”“圆周角”“圆外角”的概念,再结合圆心的特殊性,进一步给出圆内角的特殊情况——圆心角,让学生的目光聚焦在图8,从而获取圆心角的概念,并结合“对顶角相等”对“图8中相等的圆心角所对的弧是否相等”进行猜想,利用圆的旋转不变性加以论证.
问题10相等的圆心角所对的弧相等吗?若相等,请给予证明;若不相等,请举例说明.

图14
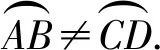
问题11线段有长度.弧也是线,弧的长度又该如何计算呢?
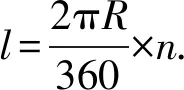
问题12线段有中点,那弧是否也有中点?如果有,请你找出弧的中点.
设计意图回顾尺规作图找线段中点的方法,结合圆心角定理可知作弧所对弦的垂直平分线与弧的交点即为弧的中点,更好地体现了弧与弧所对弦之间的关系,也进一步感悟数学的度量方式,感知“化曲为直”的思想,逐步形成空间观念和几何直观,也能结合图12给出“弓形”“弓高”“弦心距”等相关概念.
5.4 圆周角定理
结合学生所画的图形,教师引导学生借鉴圆心角及相关定理,给出圆周角的概念,重点突出圆周角与其所对弧、弧所对的圆心角、所对弦之间的数量关系,自然引出圆周角定理以及相关推论.
问题13根据图10,以类比的方式给出圆周角的概念,进一步观察圆心与其位置关系.
设计意图教师引导学生从圆心角出发,结合角的定义,类比得出圆周角的概念.再根据圆心与其位置关系,在学习单中画出3种情况(如图15~17),为之后学习圆周角定理做铺垫.

图15 图16 图17
问题14同弧(或等弧)所对的圆周角与圆心角之间有何数量关系?
设计意图用弧来构建“两角”之间的关联,引导学生用画图的方式去猜想二者之间的数量关系,即一条弧所对的圆周角是圆心角的一半.通过特殊弦(直径)将圆周角问题转化为圆心角问题.对图15、图16的论证比较简单,对图17的论证学生可能会遇到一定困难,教师适当引导学生用代数方法(即“设元”)找出角度之间的数量关系,从具体的“数”抽象到“式”,以便更好地寻找等量关系,顺势可得圆周角定理及相关推论、圆内接四边形及其性质等.

图18

设计意图借助三角形的内角、外角,再次阐述点与圆位置关系的另一种证明方法:当点与弧两端所成张角大于弧所对的圆周角时,点在圆内;当点与弧两端所成张角等于弧所对的圆周角时,点在圆上;当点与弧两端所成张角小于弧所对的圆周角时,点在圆外.从而进一步说明圆周角在圆的基本性质中的重要地位.
6 教学的思考
6.1 关注几何通性,构建单元整体教学
教学内容的设计应符合学生的认知规律,且有助于学生理解,实现“四基”,发展“四能”,以适合学生的发展为原则将教学内容进行结构化整理,使知识系统化,以螺旋式教学的方式,拓宽和加深教学内容,真正落实数学核心素养.把握单元教学目标,构建单元教学以便更符合学生对几何内容的理解.“圆的基本性质”是直线的拓展和衍生,可以借鉴直线的相关研究.本单元教学设计从直线出发,给出圆的基本性质,让学生突破“只见树木,不见森林”的学习困境,真实感受知识之间的联系,实现“数”与“形”之间的相互转化,并学会用数量关系来展现几何图形的基本性质,引导学生养成“见形思数”的数学习惯.无论是在教法还是在学法上都彰显了几何的通性,实现了几何教学的统一.
6.2 以问题串引领教学,以课堂资源优化教学
基于问题驱动教学,根据学生心理和教学内容,以问题串引领教学,将教学内容转化为一个个问题,通过学生回答,教师得到反馈,再提出新问题,引导学生将所学知识从基础出发进行发现、深入和外延,在加大知识广度的同时,也加深了知识的深度.这样的教学更有利于知识的系统化,适合单元教学.环环相扣的问题串,从一个问题出发引出一个知识点,再由其引出另一个问题,将圆的基本性质以串的形式呈现给学生.本单元知识点的引入始终围绕弦与弦的位置关系,利用学生所画的图形抽象出数学几何概念,并对图形性质进行研究,抓住单元知识之间的关联,重组教学内容,以问题串的教学思路引领学生思辨,“奇思妙想”给出图形,完美优化课堂资源,结合“见形思数”思路实现单元整体教学.本单元的整体设计,学习资源来源于学生的“课堂资源”,将其再服务于探究中,激励学生参与教学的积极性,有助于更好地落实“四基”,实现“四能”的发展[4].
6.3 优化思维结构,彰显学科育人
以知识为载体,关注学生的数学思维方法,实现数学学科的育人价值,着眼于学生的终身发展才是数学教学的本质.俗话说得好,人生的意义不在于长度而在于宽度.思维上的宽度和深度决定了学生的一生,而“问题串”教学很好地弥补了传统教学对课外知识的外延和课内知识挖掘的不足,能更好地彰显数学本质.本单元的设计以学生所画的图形为切入点,构建弦与弦的各种位置关系再进行研究,体会从问题解决中概括出一般结论,形成数学研究的方法与策略,感悟用数学的眼光观察世界的意义,提高学生学习数学的兴趣.
教学方法千千万万,适合学生的才是好方法.教师要学会重组教材内容、构建知识结构,在教学中把握知识的整体性,发展学生思维的系统性、思想的一致性,让学生感知研究方法的迁移类比.在研究过程中,采用从“整体到部分”再由“部分到整体”、从“特殊到普遍”再由“普遍到特殊”的方式,更加符合学生的认知.将圆的知识与直线类比学习,感知知识的统一、思维的统一,找到知识之间的关联,以实现教法的迁移,推进“教—学—评”一致性,让学生从“学会了”转化成“会学了”,真正实现思维的发展.

