中国古代数学融入小学数学课堂的路径初探——以HPM视角下“圆的面积”的教学为例

山东青岛西海岸新区星光岛小学（266427） 孙 伟

小学数学教育应当充分发挥中华优秀传统文化在学科育人方面的作用。中国古代数学是中华优秀传统文化的重要组成部分，如何将其融入数学课堂是一个值得探讨的问题。

一、中国古代数学融入小学数学课堂的路径

数学史与数学教育之间的关系研究，即“HPM”，是数学教育研究的一个领域，主要关注如何将数学史融入数学教学中，以发挥数学史的教育作用，提高学生的数学核心素养，实现数学教育的育人价值。这种理念与弘扬中华优秀传统文化的要求是一致的。因此，从HPM 视角实施小学数学教学能够展现中华优秀传统文化的独特教育价值。

HPM 的研究经历了从关注数学史与数学教育的关系，到关注如何将数学史融入数学课堂，再到关注如何培养学生的文化自信和民族自豪感的发展过程。在这个过程中，HPM 不断拓展其研究领域，创新其研究方法，它可以为本次实践探索提供思路和策略。本文以青岛版教材六年级上册“圆的面积”教学为例，从HPM 视角初步探索将中国古代数学融入数学课堂的路径。

（一）整理史料

史料是研究的基础，必须真实可靠。教师可以从可靠的文献资料中整理史料，比如发表的论文和出版的书籍等。HPM 认为个体知识的发生遵循人类知识的发生规律，因此教师可以按照知识发生的顺序整理史料。整理针对某一问题的史料时，应尽可能详细，要找各地区的史料，要关注每个时期这一问题的历史背景和文化环境，还要关注每个时期这一问题的研究方法，边整理、边对比、边归类。以下是笔者按照知识发生的顺序整理的“圆的面积”的史料。

1.无意识几何阶段

古代人类对太阳、月亮等的崇拜和好奇，促使他们抽象出日月的共同特点——圆。在夏朝，人们制造了带有两个圆形车轮的马车，制作了圆口圆底的彩陶罐，这些实践活动和文化遗迹表明，在无意识几何阶段，人们对圆形的认识是通过对自然界的观察和实践活动的抽象得出的。

2.经验几何阶段

《周髀算经》中有“周三径一”的说法。这个结论可能是人类经过大量的实践或者实验得出的近似结果。

古埃及的《莱因德纸草书》中也有铺谷粒求圆面积的方法。

古印度人采用直观的方式研究圆的面积，其中一种方法是将圆切成许多相等的小瓣，转化为一个近似长方形来求面积。

由此可见，在经验几何阶段，人们开始运用观察法、测量法和实验法来建立圆形和直线图形之间的联系。通过实际观察和实验，他们不断积累经验，逐渐总结了圆的周长和面积的计算方法，然而，这些方法的结果往往是近似的。

3.论证几何阶段

《九章算术》中提到的“半周半径相乘，得积步”是一个精确的圆面积计算公式。在刘徽之前，人们在求证这个圆的面积公式时，通常使用圆内接正十二边形来代替圆，然而，刘徽认为这种证明方法并不严谨，因为内接正多边形和圆形之间还存在弓形部分。他认为“割之弥细，所失弥少”。接着，他得出了“以一面乘半径，觚而裁之，每辄自倍，故以半周乘半径而为圆幂”的结论。

刘徽的贡献在于首次引入了极限和无穷小的概念，将其运用于数学证明中。这是思维方式的一次重大突破，代表了数学思维的质的飞跃。

阿基米德提出并证明了“圆的面积等于一条直角边为圆半径、另一条直角边为圆周长的直角三角形的面积”。开普勒提出分割法。

由此可见，在论证几何阶段，人类逐渐认识到，依靠经验得出的结论有时是正确的，有时是错误的。为了寻求更准确的计算方法，人们开始尝试提出公式并证明。论证过程中的共同点是构建一个与圆面积相等的直线图形。

通过整理史料，笔者发现圆的面积的探究过程是一个从实验研究到演绎推理研究的过程，是一个从近似计算到精确计算的过程，是一个从“以直代曲”到“无限逼近”的过程。其中的重要节点有：得不到准确面积时，就“以直代曲”求近似面积；改进直线图形，使其“逼近”圆形，推出圆的面积公式；用极限思维和无穷切割法证明公式。

综上所述，按知识发生的顺序整理史料，有助于教师整体把握知识的发展进程，找到知识发生的重要节点；边整理、边对比、边归类，有助于教师发现其中的规律和特点，从而更好地理解其数学本质；尽可能详细地整理史料，能为小学数学课堂教学提供更多生动有趣的素材和资源，培养学生的数学核心素养，激发学生的学习兴趣。

（二）筛选史料

汪晓勤教授认为，选择史料时，需要根据教学目标和学生实际情况进行筛选，以确保史料能够辅助教学，提升教学效果。因此，教师可以考虑将“割圆术”融入数学课堂。

首先，从教学目标来看，“割圆术”这一段史料蕴含了“以直代曲”和“无限逼近”的思想方法，这两种思想方法在数学学习和现实生活中都有着广泛的应用。通过学习“割圆术”，学生可以了解到如何用简单的直线图形来逼近曲线图形，这种思想方法的掌握对于学生未来的数学学习和实际应用都有很大的帮助。同时，“割圆术”也体现了中华民族的优秀传统文化，将其融入数学课堂可以增强学生的文化自信和民族自豪感。

其次，从学生实际情况来看，“割圆术”这一段史料符合学生的实际情况和学习需要。学生在之前的学习中已经积累了“出入相补”的知识，理解了“等积变形”的数学思想，这些知识点与“割圆术”所蕴含的思想方法密切相关。同时，学生在学习“圆的周长”这一课时中，也已经初步体会了“以直代曲”的思想方法，这也为进一步学习“割圆术”打下了基础。因此，将“割圆术”融入课堂教学可以帮助学生将之前所学的知识点进行联系和深化，解决学生在学习“圆的面积”时遇到的困难和问题。

总之，合理选择史料并将其融入数学课堂是提高教学质量和促进学生发展的关键要素，值得教师不断探索和实践。

（三）应用史料

现代学生与古代数学家在知识经验、思维方式及学习方法等方面存在差异。对此，教师将史料融入数学课堂时需要结合教材和当前学情。以下是具体融入过程。

首先，梳理知识发展的重要节点及其对应的史料、教材和学情（见表1）。

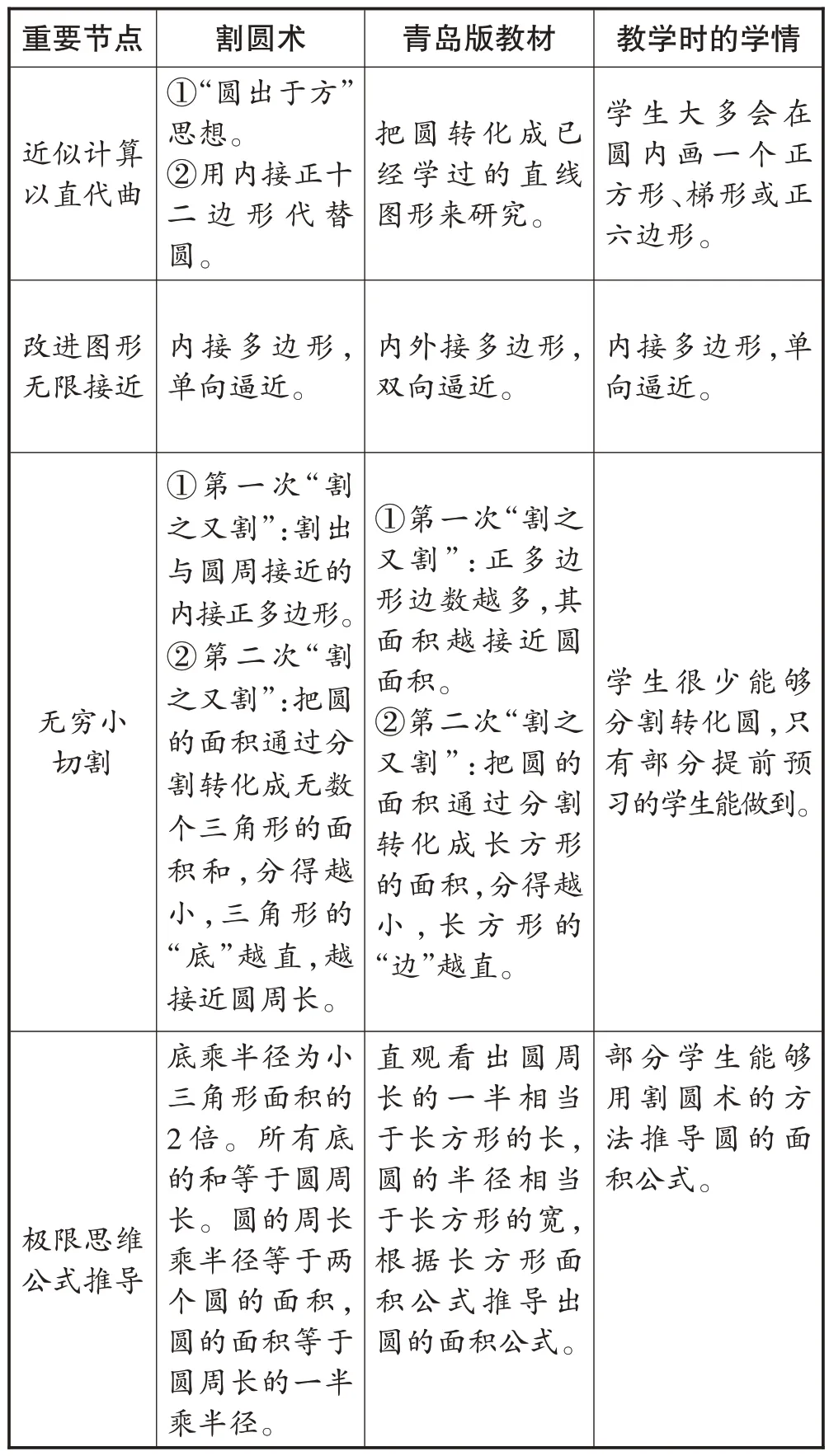
表1 知识梳理

然后，将史料与教材进行有效整合，并据此设计教学。通过上述梳理，发现史料和教材都突出了知识发展过程中的关键节点。根据学生的实际状况，笔者认为教材中的数学知识排列并未完全符合学生的心理认知顺序，这使得分割圆的必要性难以自然展现。引入“割圆术”却能够解决这一难题，可以采用“重构式”的方法将这一史料有机地融入数学课堂。图1 是“圆的面积”这一课时的教学设计思路。

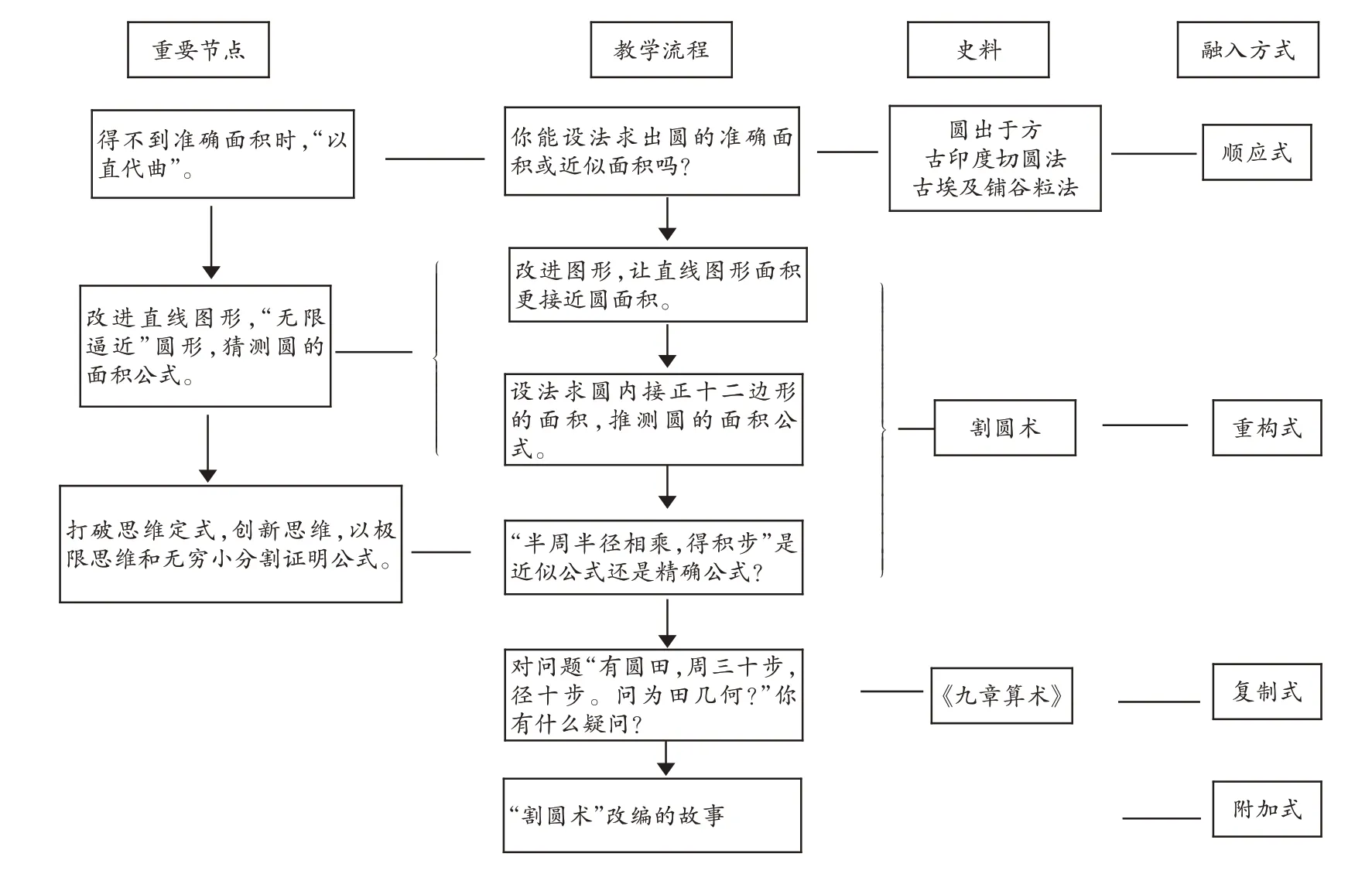
图1 “圆的面积”教学设计思路

二、评估路径的可行性和有效性

笔者利用课堂实践的评估结果检验这一路径的可行性和有效性。汪晓勤教授提出的数学史融入数学教学的六个价值理论为评估提供了理论框架。

（一）呈现知识之谐，展示方法之妙

将“圆出于方”的史料以顺应式的方式融入教学中，通过提出“你能设法求出圆的准确面积或近似面积吗？”这一问题，将“近似面积”这一概念引入课堂。这一表达方式符合学生的认知起点，能够有效地促使学生自主萌发将圆转化成直线图形的想法。

进一步以重构式的方式将“割圆术”这一史料融入教学中，引导学生不断改进直线图形，使其逐渐接近圆。在思考和探索的过程中，学生感受到“割圆”这一思想和方法的奇妙与智慧。

让学生求圆内接正十二边形的面积，引导学生自然而然地像切西瓜一样将圆形进行分割，使用三角形面积或者长方形面积来代替圆的面积，并对圆的面积公式提出猜想。

数学史的融入，让学生更好地理解圆的面积计算的发展历程和内在逻辑，提高他们的数学素养，同时解决了圆的面积公式的推导这一学习难点，学生能够体会到“以直代曲”“无穷小分割”等方法的美妙之处。

（二）营造探究之乐，提供能力之柱

笔者将《九章算术》中记载的计算方法“半周半径相乘，得积步”融入教学，并提出问题“是近似公式还是精确公式？”，促使学生开展了激烈的讨论。学生意识到，正多边形的边数越多，分割拼成的平行四边形的底越“直”，长度越接近半周长，拼成的平行四边形的高越接近半径。学生感受到了“把圆转化为其他图形”的奇妙之处。学生打破了原有思维的局限，接触了极限思维，成功突破了难点，验证了圆的面积公式。数学史的融入培养了学生的批判精神和创新精神。

（三）揭示文化之魅，彰显德育之效

在作业环节中，笔者将“割圆术”的史料改编为一个富有启发性的故事。通过阅读和思考这个故事，学生感受到数学家的质疑精神、探索精神和创新精神，感受到数学家具有耐心细致、勇于面对困难的优秀品质，感受到中国古代数学的魅力。这无形之中激发了学生的民族自豪感和文化自信。

综上所述，通过整理史料、筛选史料、应用史料的路径，可以把中国古代数学较好地融入课堂教学中。笔者期待未来能够进一步深入研究，为教育事业提供更多的启示和帮助，为教育领域带来更多的进步和突破。