探究解题策略 内化数学思想

摘 要:为把数学思想内化为解题的策略,文章以中考数学压轴题为例,强调了认真阅读题目在解题过程中的重要性,深入讨论了利用数学思想解决这类问题的基本策略,以便更好地应对一系列复杂问题的挑战,灵活应对中考数学压轴题.培养学生数学思维,提高学生运用所学知识解决实际问题的能力,从而提高数学学习的效果.
关键词:中考数学;压轴题;解题策略;数学思想
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2024)02-0071-03
收稿日期:2023-10-15
作者简介:王秋娟(1980.6-),女,福建省尤溪人,本科,中学一级教师,从事初中数学教学研究.
解题策略在中考数学中起着至关重要的作用,它不仅帮助学生有效解决具体的数学问题,更重要的是培养了学生的数学思维和逻辑推理能力[1-2].在全国各地中考数学试题中,最后一道题常常会是较难或综合性较强的问题,这就是通常所说的“压轴题”.这些题目不仅需要学生熟练掌握数学基本概念和基本技能,还需要学生灵活应用所学的知识,将数学思想内化为解题的基本策略,方能熟练应对中考数学压轴题,从而更加深入地理解数学的本质,提高学生应用所学知识解决问题的能力,进而提高数学学习成效.
1 认真审题,加深理解
随着新课程改革的不断深入,中考数学试题的形式发生了较大变化,尤其是中考数学压轴题的形式和内容都发生很大的变化.认真审题是理解问题本质的关键一步,审题的目的是全面理解题目中已知量与所求量之间的逻辑关系,确定下一步的解题思路,具体解题思路如图1所示.在理清解题思路的基础上,需结合问题特征选择合适的数学方法和思维策略解决问题,提高解题效率和准确性[3].
图1 解题思路模型图
1.1 认真阅读题目
认真反复阅读题目,并注意题目中的每个细节、要求和关键点,这有助于学生整体理解数学问题,避免因遗漏信息而导致的错误解答.在阅读过程中,要有意识地将“大”问题分解为“小”问题,这有助于帮助学生找到问题的关键点.
1.2 学会理解问题
在解决问题的过程中,要注意将数学问题分解为关键要素,包括已知条件、未知量和问题的核心要求.尝试着从不同的角度和不同思维方式理解问题.也可以尝试提出自己的问题,反问题目中的条件和要求,这有助于帮助学生深入思考问题,更全面地理解数学问题,并确定数学问题的解题方向.
1.3 弄清问题类型
在解决问题的过程中,要注意判断问题是属于哪一类数学问题,如代数、几何、概率等,这样可以为选择合适的解题方法提供线索.同时,有些题目可能包含一些隐含的信息或假设,会提供一些模式或规律,通过观察这些特征,可能可以推测出问题的解决思路,以扩展对问题的理解.
1.4 绘制图表或示意图
对于几何问题或涉及复杂关系的数学问题,绘制图表或示意图可以帮助学生更好地理解题目本质,并找到解题的线索和关键点.
1.5 确定解题方法
在解决问题的过程中,根据题目的特点和要求,选择合适的数学思想、公式或定理解决问题.这可能需要运用代数运算、几何图形的性质、概率与统计等数学基本技能.
2 探究解题策略,内化数学思想
中考数学压轴题一般为代数与几何的综合题.在这类综合题中,通常涉及较多的数学知识点,并且渗透多种数学思想方法.题目中往往涉及代数、几何、概率、统计等多个数学领域的相关知识[4].将多个数学知识点结合起来,学生要灵活运用不同的数学思想方法解决问题,如分类讨论、数形结合、推理推导等思想[5].这样不仅能够让学生复习掌握各个领域的知识,还能够锻炼他们将知识点进行融会贯通的能力.因此,要掌握中考数学压轴题的解题策略,这意味着学生需要在解题过程中综合运用多个数学知识点和数学思想解决问题,需具备扎实的数学基础知识和强大的理解能力.
2.1 试题呈现及分析
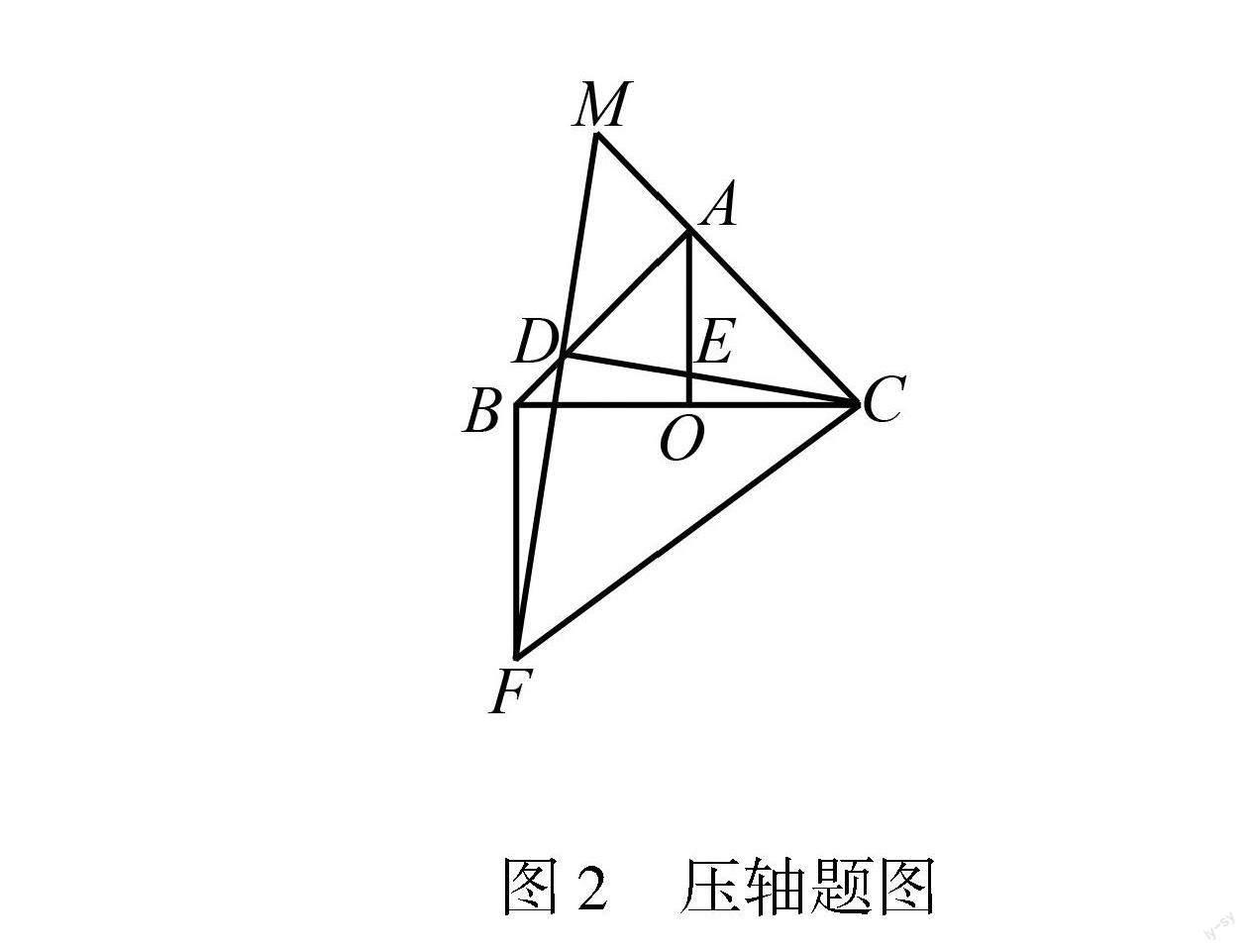
笔者以2023年福建省中考数学第25题为例,探究解决中考数学压轴题的基本策略.通过问题的解決,说明灵活运用数学思想,可将复杂的问题简单化,从而有效地解决中考数学压轴题.如图2,在△ABC中,∠BAC= 90°,AB =AC,D是AB边上不与A、B重合的一个定点.AO⊥BC于点O,交CD于点E.DF是由线段DC绕点D顺时针旋转90°得到的,FD,CA的延长线相交于点M.
图2 压轴题图
(1)求证:△ADE∽△FMC;
(2)求∠ABF的度数;
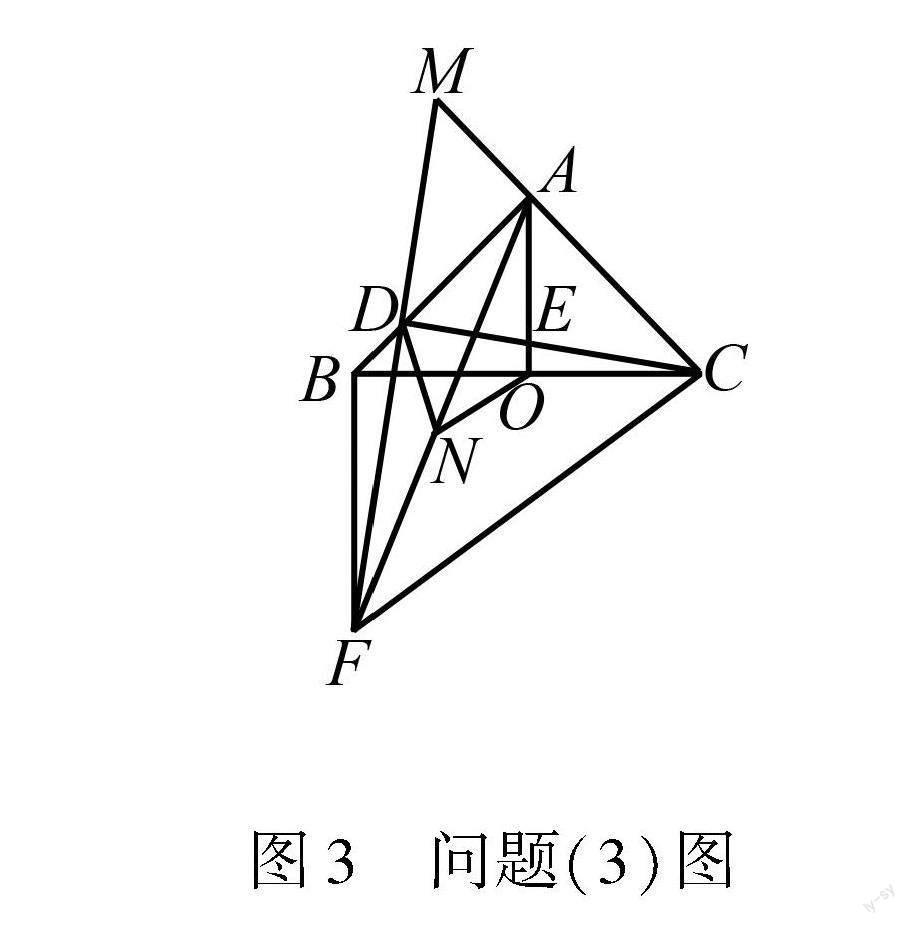
(3)若N是AF的中点,如图3,求证ND=NO.
图3 问题(3)图
分析 本题主要考查三角形内角和定理、平行线的判定与性质、全等三角形的判定与性质、相似三角形的判定与性质、等腰三角形及直角三角形的判定与性质等基础知识,考查推理能力、空间观念、几何直观、运算能力、创新意识等,考查化归与转化思想、数形结合思想、函数与方程思想等.对于问题(1),学生需根据已知条件,善于用相似三角形判定定理去证明;对于问题(2),要求学生求∠ABF的度数,那么需要学生能够找到相关联的相似三角形,然后根据边角关系,巧用转换思想进行解答;对于问题(3),学生需构造辅助线,根据平行线的性质找到对应角的关系,然后运用全等三角形的判定、等腰三角形、直角三角形性质等知识解决问题.因此,解答本题需要有较强的综合解题能力和灵活的数学思维.
2.2 善用相似三角形判定定理
对于问题(1),主要考查相似三角形的判定定理,即两角分别相等的两个三角形相似.
如图2,因为DF是由线段DC绕点D顺时针旋转90°得到的,所以∠FDC=90°,FD=CD,∠DFC=45°.因为AB=AC,AO⊥BC,所以∠BAC=2∠BAO.因为∠BAC=90°,所以∠BAO=∠ABC=45°,所以∠BAO=∠DFC.因为∠EDA+∠ADM=90°,∠M+∠ADM=90°,所以∠EDA=∠M,所以△ADE∽△FMC.
2.3 巧用关系转换思想
对于问题(2),题目主要考查相似三角形的性质,即相似三角形的对应角相等,对应边成比例.解决此问题需巧用转换思想,分别求出∠ABC和∠CBF的度数.具体求解过程如下:
设BC与DF的交点为I,如图4所示.因为∠DBI=∠CFI=45°,∠BID=∠FIC,所以△BID∽△FIC,所以BIFI=DICI,即BIDI=FICI.又因为∠BIF=∠DIC,所以△BIF∽△DIC,所以∠IBF=∠IDC.因为∠IDC=90°,所以∠IBF=90°.因为∠ABC=45°,所以∠ABF=∠ABC+∠IBF=135°.
2.4 妙用平面几何思维
对于问题(3),一是考查全等三角形判定定理,即两边及其夹角对应相等的三角形是全等三角形,两角及其夹边对应相等的三角形全等;二是考查等腰三角形性质,即等腰三角形的顶角的平分线、底边上的中线、底边上的高线互相重合;三是考查直角三角形性质,即直角三角形的两个锐角互余,直角三角形斜边上的中线等于斜边的一半.具体证明过程如下:
图5 问题(3)解答图
如图5,延长ON交BF于点T,连接DT,DO.因为∠FBI=∠BOA=90°,所以BF∥AO,所以∠FTN=∠AON.因为N是AF的中点,所以AN=NF.又因为∠TNF=∠ONA,所以△TNF≌△ONA,所以NT=NO,FT=AO.因为∠BAC=90°,AB=AC,AO⊥BC,所以AO=CO,所以FT=CO.由(2)知,△BIF∽△DIC,所以∠DFT=∠DCO.又因为DF=DC,所以△DFT≌△DCO,所以DT=DO,∠FDT=∠CDO,所以∠FDT+∠FDO=∠CDO+∠FDO,即∠ODT=∠CDF.因为∠CDF=90°,所以∠ODT=∠CDF=90°,所以ND=12TO=NO.
3 结束语
在中考试题中,压轴题承载着一定的选拔性功能,具有一定的难度,综合性较强.为了帮助学生更好地解决中考数学压轴题,在初中数学教学中,教师要引导学生掌握其解题策略.为此,学生需要先进行认真审题,深度理解题目中已知量与所求量之间的逻辑关系,只有这样,才能在千变万化的题目中灵活运用数学基础知识和基本技能解决问题.数学思想方法在解决中考数学压轴题时非常有效,在解决问题过程中,学生可结合已经学习过的数学概念、公式、定理等,灵活运用它们简化问题,分析问题的解决思路.因此,掌握解題策略和内化数学思想对于解决中考数学压轴题非常重要.通过合理应用这些策略,才能够更系统、有条理地解决问题,充分发挥学生的数学思维能力和解题技巧.
参考文献:[1]
丁素琴.关注解题过程 探究解题策略:以一道关于抛物线的中考压轴题为例[J].数学教学通讯,2022(2):70-71.
[2] 彭小珍.探究解题策略 提升数学思维[J].上海中学数学,2021(Z1):81-83,86.
[3] 许景初.立足基础,稳中求新,凸显素养:对一道数学中考压轴题的探索[J].中学数学研究,2021(20):44-47.
[4] 王元迪.数学思想在高中解题中的策略探析[J].中学数学,2020(23):38-39.
[5] 秦琴.感悟数学思想,探寻解题策略的多样化:以苏教版数学课本一道实际问题教学为例[J].数学大世界(中旬),2019(09):74,76.
[责任编辑:李 璟]

