中考二轮复习微专题探究

刘长松 陈超

摘  要：微专题的复习具有短小、精炼、实战性强等特点，文章以含参数的二次函数中对称轴、区间、函数值之间的关系为例，列举了四类基本问题：定轴定区间、定轴动区间、动轴定区间、动轴动区间.重点解决定轴动区间、动轴定区间、动轴动区间问题，复习巩固数形结合、分类讨论等思想方法，学会寻找关键界点，对照图形、分类讨论、动中取静，体会“数缺形时少直观，形少数时难入微”的数形结合思想方法，感受数学的运动美、对称美.

关键词：二次函数；对称轴；区间；函数值；分类讨论

中图分类号：G632    文献标识码：A    文章编号：1008-0333（2024）02-0020-03

收稿日期：2023-10-15

作者简介：刘长松（1982.9-），男，江苏省盐城人，本科，中学高级教师，从事初中数学教学研究.

基金项目：本文系江苏省苏州市教育科学“十四五”规划课题“深度学习视角下初中数学微专题设计的实践研究”的阶段性成果（项目编号：2021/C/02/019/03）

二次函数问题一直是中考的热点问题，其中函数的取值范围及最值问题一直是困扰学生的难点，此类问题的突破也是困扰一线教师的难点.这类问题往往穿插在综合题中，有很强的区分度和选拔功能，对学生的空间想象、数形结合能力要求比较高，如何依据条件合理分类讨论是关键.笔者以近5年江苏省乃至全国各地的中考试题为例，分析含参数的二次函数的区间、对称轴、函数值的关系问题，以期抛砖引玉，供读者参考.

1 问题背景

含参数的二次函数问题主要是指二次函数关系式中含有参数或者给定的区间中含有参数.这类问题形式多样，常见的题型有：求参数的值或范围、讨论二次函数的最值、解含参数的二次不等式、不等式的恒成立问题、一元二次方程的根的分布情况、二次函数的图像与直线的交点个数问题等，这类问题属于高中二次函数知识点在初中的渗透.近些年在江苏省内外的中考中时常出现，如南京2021年第26题、2020年第16题、2017年第26题；南通2021年第26题、2020年第25题、2019年第26题、2018年第26题；扬州2017年第8题；泰州2021年第25题、2018年第24题；北京2021年第26题、2020年第25题、2019年第26题、2018年第26题；大连2021年第26题、2020年第25题、2019年第26题、2018年第26题；杭州2021年第22题、2020年第22题、2019年第22题、2018年第22题，等等.

2 常见题型

2.1 定轴定区间问题

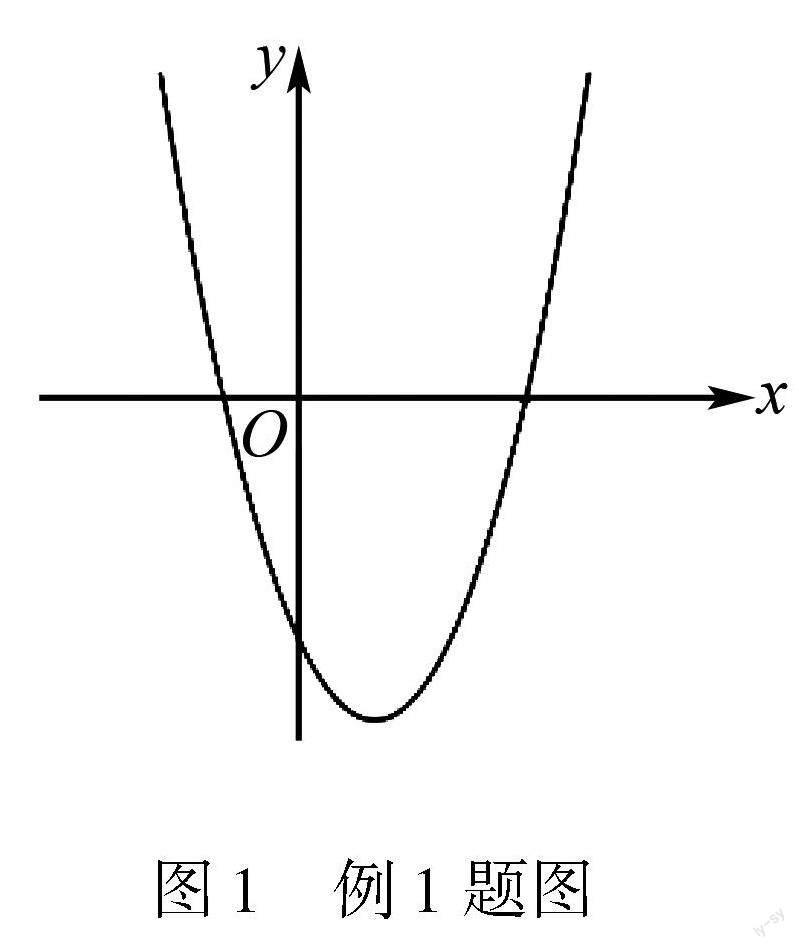
例1  如图1，已知二次函数y=x2-4x-5.

（1）当-1≤x≤0时，y的取值范围是   ；

（2）当3≤x≤4时，y的取值范围是  ；

（3）当0≤x≤3时，y的取值范围是  ；

（4）当-5≤y≤0时，x的取值范围是  ；

请说一说二次函数的对称轴和区间之间的关系［1］.

本题给定了二次函数的表达式，从两个不同角度设计问题，一是已知自变量x的取值范围求对应的函数值y的取值范围；二是已知函数值y的取值范围求对应的自变量x的取值范围.共设置了4个小问题，分别是x的取值范围都在对称轴的同侧（左侧或右侧），取值范围从对称轴左侧增加到对称轴右侧，包含顶点的这种情况.设计问题（1）（2）（3）的目的是为了引导学生在已知x的取值范围时，要分两种情況讨论，即在对称轴同侧和异侧，对于异侧的这种情况要找三个界点来确定函数值的取值范围.初步让学生感知对称轴确定时如何求函数值的取值范围.设计问题（4）的目的是感知函数值y的取值范围一定时，x会有两部分取值范围，进一步感受二次函数的对称美．

2.2 定轴动区间问题

例2  已知二次函数y=x2-4x-5.

（1）当m≤x≤m+1（m为常数）时，函数的最小值为1，则m=；

（2）若此二次函数在0≤x≤m（m为常数且m>0）的图像的最高点与最低点的纵坐标之差为h，写出h关于m的函数关系式［2］.

本题已给定二次函数的表达式，由二次函数的性质易知其对称轴为直线x=2，问题（1）中给定的x的取值范围是一个随着m的变化而变化的动区间，在这个动区间里，函数值最小值为1，如何引导学生思考怎样确定参数m的取值是关键．问题（2）中x的取值范围为0≤x≤m，而对称轴为直线x=2，所以函数图象经过一组对称点（0，-5），（4，-5）.参数m的取值需要分三种情况进行讨论，即0≤m≤2，2< m≤4，m＞4.

2.3 动轴定区间问题

例3利用二次函数的性质解答下列问题：

（1）已知二次函数y=x2-2mx-3（m为常数），当x＜1时，y随x的增大而减小，m的范围是  .

（2）二次函数y=x2-2mx+2m2（m为常数），当2≤x≤5时，y的最小值为1，m=  .

本题涉及的取值范围属于一个定区间，但是二次函数关系式中含有参数m，从而二次函数图象的对称轴是随着参数m的变化而变化的动轴.在问题（1）中，当x＜1时，y随x的增大而减小，由二次函数的性质易求得它的对称轴是直线x=m，而此抛物线开口向上，可以确定对称轴在直线x=1的右侧，进而可得参数m的取值范围；在问题（2）中，二次函数图象的对称轴是直线x=m，它是一条动直线，而给定的区间是2≤x≤5，它是一个定区间，因此可以分为三种情况进行分类讨论：①当m≤2，x=2时，y取得最小值1；②当2＜m＜5，x=m时，y取得最小值1；③当m≥5，x=5时，y取得最小值1．

2.4 动轴动区间问题

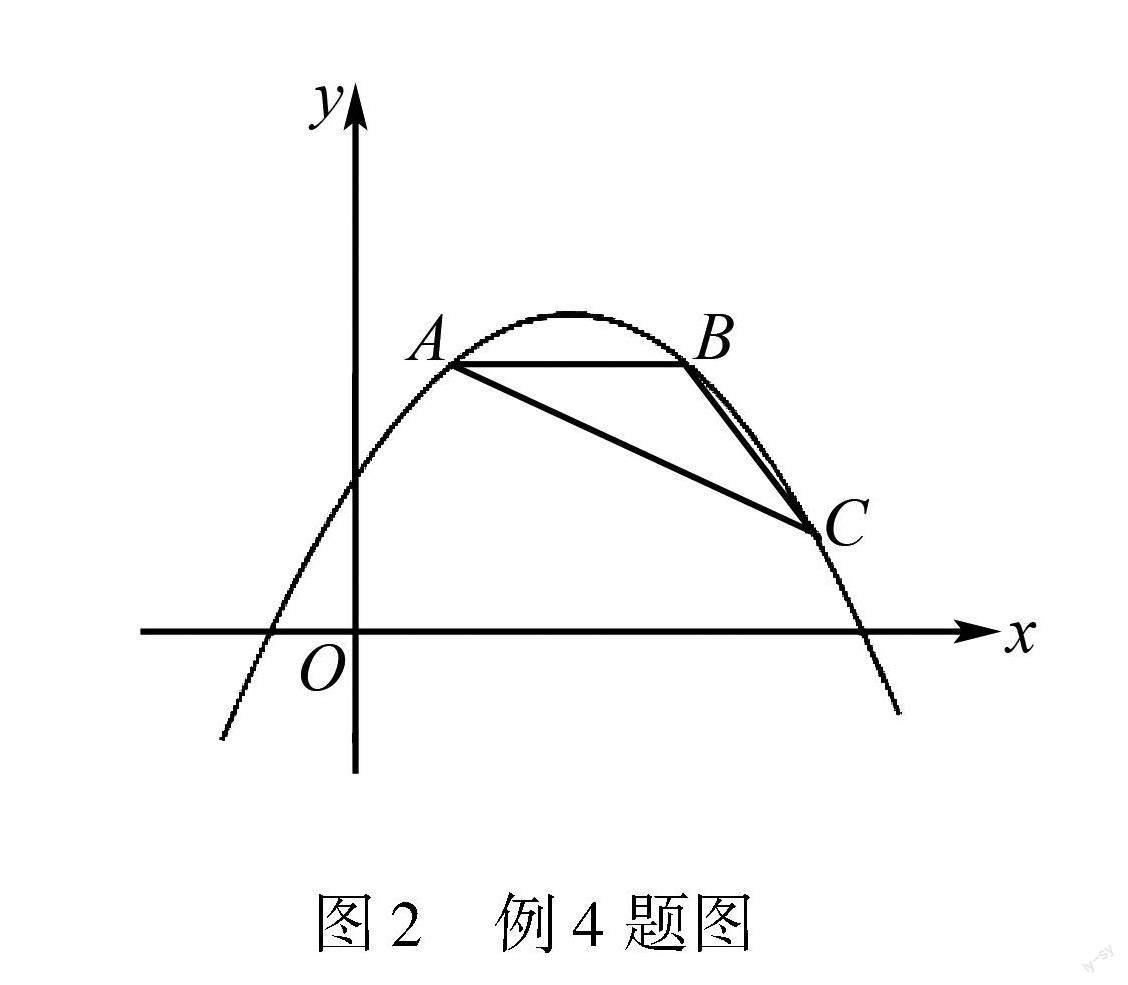
例4  如图2，点A，B，C都在抛物线y=ax2-2amx+am2+2m-5（-14

（1）抛物线的顶点坐标为   .（用含m的代数式表示）；

（2）△ABC的面积为  .（用含a的代数式表示）；

（3）若△ABC的面积为2，当2m-5≤x≤2m-2时，y的最大值为2，则m=   .

本题是二次函数综合题，主要考查二次函数图象上点的坐标特征、等腰直角三角形的性质、一元二次方程的解法及二次函数最值的求法，解决本题的关键是：①利用配方法将二次函数解析式变形为顶点式；②利用参数求出点C的坐标；③分别按m＜2，2≤m≤5及m＞5三种情况进行分类讨论．

2.5 二次函数图象与直线的交点个数问题

在含参数的二次函数问题中，二次函数图象与直线的交点个数问题也是近年中考的热点问题.

例5  已知二次函数y=ax2+bx+c的图象经过（-2，1），（2，-3）两点．

（1）求b的值；

（2）设点（m，0）是该函数的图象与x轴的一个公共点．当-1＜m＜3时，结合函数的图象，直接写出a的取值范围［4］．

本题主要考查二次函数的图象与性质，解决本题的关键在于理解二次项系数a对函数图象的影响，包括开口方向和开口大小，都要熟记于心，否则问题（2）很难正确解答；在问题（2）中，将（m，0）代入y=ax2+bx+c中，写出判别式的值，根据图象经过（-2，1），（2，-3）兩点，分-1＜m＜2和2＜m＜3两种情况讨论即可．

例6  已知二次函数y=x2-4x+3a+2（a为常数）．在同一平面直角坐标系中，若该二次函数的图象在x≤4的部分与一次函数y=2x-1的图象有两个交点，求a的取值范围．

本题是由南通市2019年中考题改编而来的，可根据二次函数的图象与一次函数y=2x-1的图象有两个交点，则方程x2-4x+3a+2=2x-1的判别式Δ＞0，易求得a＜2.将x＝4和代入y=2x-1，求得函数值y=7.将（4，7）代入y=x2-4x+3a+2，可得到关于a的一元一次方程，解方程即可求得a=53.根据题意求出a的取值即可.本题主要考查二次函数的图象和性质、一次函数的性质、一元二次方程的根的判别式、一元一次方程的解法等知识，其综合性较强，具有一定的难度．

3 结束语

中考二轮复习是一个非常关键的总结提升阶段.二轮复习不是单纯地做练习、讲练习，教师要深度把握中考的方向，研究中考命题规律，从学生的实际情况出发，提高复习的效率，总结出一些适合学生的学习方法.微专题就是一种很好的形式，精炼实用.这样的研究任重道远，需要一线教师系统地研究规律、总结方法，要善于对题型进行归类，善于引导学生进行分析、探索、归纳和总结，培养学生的思维能力，从而使学生逐步掌握自主的学习方法.

参考文献：［1］ 施海鹰.中考复习：二次函数的考点剖析［J］.科学大众（科学中考），2021（8）：21-23.

［2］ 于彬，单雪梅.一题，一类，一课：以“二次函数专题复习铅垂高模型”为例［J］.中学数学，2021（24）：34-35.

［3］ 程国云.含有参数的二次函数最值问题［J］.试题与研究（教学论坛），2016（26）：16-19.

［4］ 吕梅英.认清本质抓关键：浅析2012年中考二次函数考点［J］.中学数学，2012（24）：61-62.

［责任编辑：李  璟］