等腰三角形的存在性问题探究


摘 要:等腰三角形是初中数学中常见的一类特殊三角形,其与抛物线相结合的存在性问题是中考的热点问题,也是难点问题,具有一定的选拔功能.在初中数学教学中,可借助网络画板进行实验探究,让点动起来,让学生在形象且直观的现实情境中理清已知条件与所求结论之间的逻辑关系,然后引导学生利用所学知识给出问题的求解方法.
关键词:等腰三角形;抛物线;动点;存在性问题
中图分类号:G632 文献标识码:A 文章编号:1008-0333(2024)02-0011-03
收稿日期:2023-10-15
作者简介:郎春林(1982.2-),男,江苏省扬州人,本科,中学二级教师,从事初中数学教学研究.
存在性问题是指根据数学问题所给定的已知条件,探究是否存在符合要求的結论.存在性问题是探索型数学问题中一种非常典型的问题,其探索的方向是明确的,探索的结论有两种,即存在或不存在.与等腰三角形有关的存在性问题倍受命题者的青睐,等腰三角形与抛物线相结合的存在性问题在中考试题中经常出现,其具有一定的难度,“两圆一线定位置,边角相等分类列”是解决这类问题的基本思路与方法.本文以2017年贵州省安顺市中考的抛物线试题为例,呈现这类问题的求解思路,以期提高学生的解题能力.
1 问题呈现
(2017年贵州省安顺市中考数学第26题)如图1,直线y=-x+3与x轴、y轴分别交于B,C两点,经过B,C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
(1)求该抛物线的解析式.(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
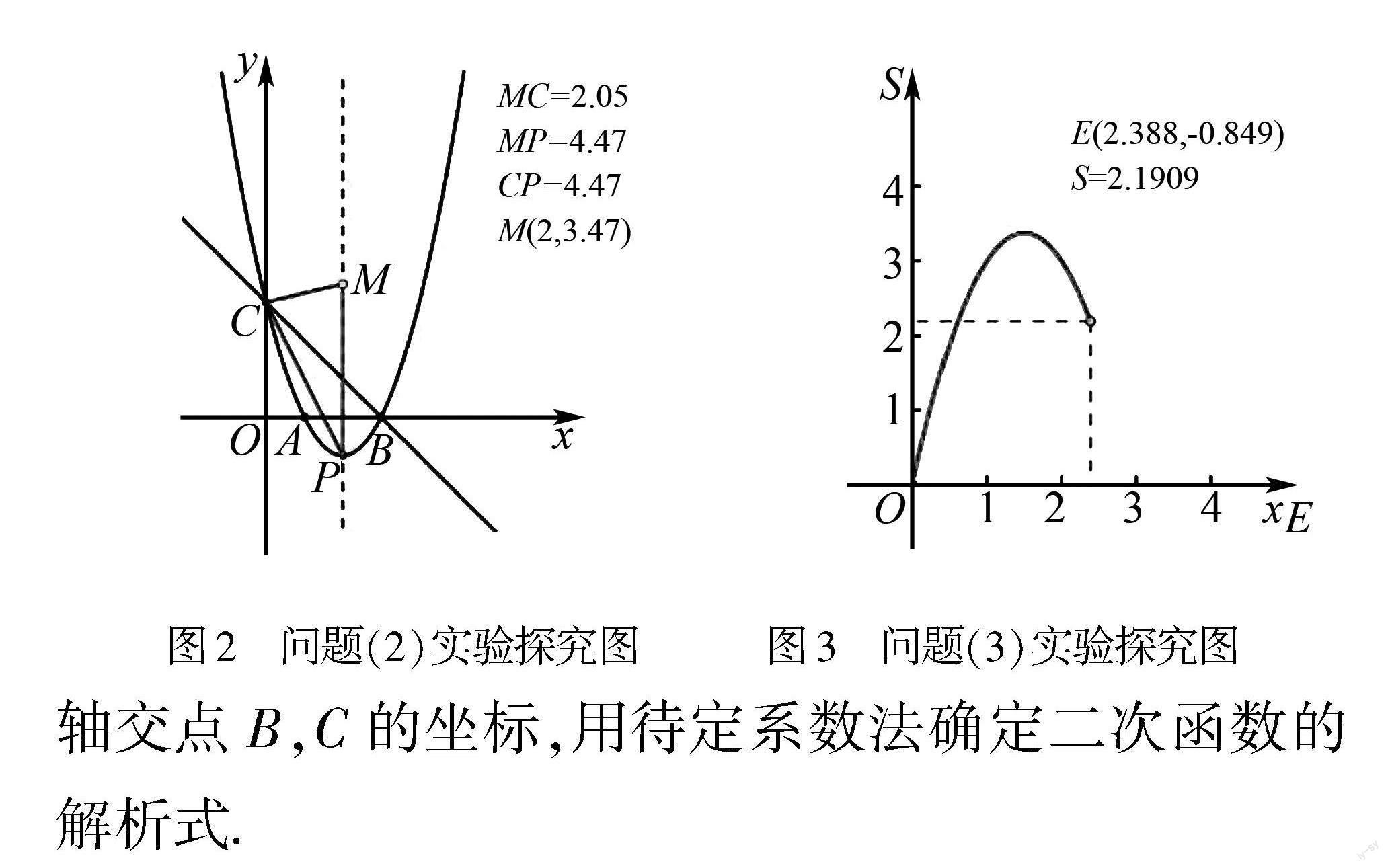
(3)当0 2 探究实验 对于问题(2),如图2所示,拖动点M,观察△PCM三边长度的变化,是否存在等腰三角形的情形? 有几种情况? 对于问题(3),如图3所示,拖动点E,观察△CBE的面积S和点E的横坐标xE变化关系的图象,猜测S是xE的什么函数. 3 思路分析 对于问题(1),求出直线y=-x+3与x轴、y轴交点B,C的坐标,用待定系数法确定二次函数的解析式. 对于问题(2),可用两种不同方法求解. 方法1(几何法):由题意知,PC长度确定,PM,CM长度是变化的,并未说明PC是腰或底,因此需分MC=MP,CM=CP,PM=PC三种情况讨论.动点M在对称轴直线x=2上. 用“两圆一线”法确定点M的位置,即作出线段PC的垂直平分线,或分别以点C,P为圆心,PC长为半径作圆,与抛物线对称轴交于点M1,M2,M3,M4,如图4所示,所以满足条件的点M只有4个,再结合条件求出点M的坐标. 方法2(代数法):设M(2,m),根据勾股定理,可利用含m的代数式表示出三角形三边的长,需分MC=MP,CM=CP,PM=PC三种情况列方程,可求得M点的坐标. 对于问题(3),过点E作x轴的垂线FE,交直线BC于点F,设点F(x,-x+3),Ex,x2-4x+3,用“宽高公式”表示出△CBE的面积,然后根据二次函数的性质即可求出面积的最大值. 4 解法探究 根据以上思路,可给出问题的具体求解过程. (1)解 因为直线y=-x+3与x轴、y轴分别交于点B,C,易知B(3,0),C(0,3).从而易求得该抛物线的解析式为y=x2-4x+3. (2)解法1 (几何法)存在点M.因为y=x2-4x+3=(x-2)2-1,所以该抛物线对称轴为直线x=2,顶点为P(2,-1). ①如图5,当MC=MP时,过PC中点D作直线l⊥PC于点D,交直线x=2于点M1,过点P作PE⊥y轴于点E,则PC=42+22=25,所以PD=5.因为M1P∥y轴,所以∠PCE=∠DPM1,所以 cos∠PCE=cos∠DPM1,即CEPC=PDPM1=425=5PM1,所以PM1=2.5,所以M12,1.5. ②如图6所示,当PM=PC时,易求得M2(2,25-1),M3(2,-25-1). ③如图7所示,当MC=PC时,过点C作CF⊥PM4于点F,过点P作PE⊥y轴于点E,所以四边形CEPF是矩形,则PF=CE=4,易求得M4(2,7). 综上可知,存在满足条件的点M,其坐标为2,1.5或(2,7)或(2,-1+25)或(2,-1-25). 解法2 (几何法)存在点M. ①如图8所示,作PC的垂直平分线交PC于点D,交抛物线的对称轴于点M1,则CM1=PM1,所以△PCM1是等腰三角形,所以点M1为所求.过点D作y轴的平行线,过点C作x轴的平行线,两直线相交于点E,过点M1作y轴的垂线交ED于点F. 因为P(2,-1),C(0,3),点D是PC的中点,所以D(1,1).因为抛物线的对称轴为直线x=2,所以CE=1,FM1=1,DE=2.易知△CED∽△DFM1.所以CEED=DFFM1,易知DF=0.5.从而可知M12,1.5. ②如图9所示,以P为圆心,PC长为半径作⊙P,交抛物线的对称轴于点M2,M3,连接CM2,CM3,则PC=PM2=PM3,所以△PCM2,△PCM3都是等腰三角形. 过点M2作y轴的垂线,垂足为E,延长CP交⊙P于点D,过点D作x轴的垂线交EM2的延长线于点F,连接M2D.易知△ECM2∽△FM2D,所以ECEM2=FM2FD.易知m-32=2m+5,所以m=-25-1或m=25-1,所以点M2(2,25-1),M3(2,-25-1). ③如图10所示,以C为圆心,PC长为半径作⊙C,交抛物线的对称轴于点M4,连接CM4,则PC=CM4.延长PC交⊙C于点D,连接DM4,则△PCM4是等腰三角形.易知M4(2,7). 综上可知,存在满足条件的点M,其坐标为2,1.5或(2,7)或(2,-1+25)或(2,-1-25). 解法 3(代数法): 因为y=x2-4x+3=(x-2)2-1,所以抛物线对称轴为直线x=2,顶点为P(2,-1).设M(2,m),又C(0,3),所以MC2=22+(m-3)2=m2-6m+13,MP2=(m+1)2,PC2=22+(-1-3)2=20,因為△CPM为等腰三角形,因此分三种情况讨论: ①当MC=MP时,则有m2-6m+13=(m+1)2,解得m=1.5,此时M2,1.5; ②当MC=PC时,有m2-6m+13=20,解得m=-1(与P点重合,舍去) 或m=7,此时M(2,7); ③当MP=PC时,则有(m+1)2=20,易得 M(2,-1+25)或(2,-1-25). 综上可知,存在满足条件的点M,其坐标为2,1.5或(2,7)或(2,-1+25)或(2,-1-25). (3)当0 5 结束语 对于等腰三角形与抛物线相结合的存在性问题,可以把解题方法总结为“两圆一线定位置,边角相等分类列”.这里的“两圆一线”法是已知等腰三角形一边长度确定(这边的端点至少有一个是定点),可以根据等腰三角形的性质作两个辅助圆,或已知边上的垂直平分线确定点的大致位置或解的个数,借助代数法求解,或利用定长线段所在直径所对的圆周角是直角构造“一线三等角”相似模型的求解方法. 通过探究这类问题的求解方法,能有效提高学生分析问题和解决问题的能力. 参考文献:[1] 郑利年,陈国玉.用角的关系,求动点的坐标[J].中学数学研究(华南师范大学版),2023(14):33-35. [责任编辑:李 璟]

