小学数学课堂提问的实践与思考
查秀琴
(怀宁县三桥镇中心学校 安徽安庆 246100)
提问,是教师组织教学的形式,也是教师实施教学的手段。小学数学是由一个个“小小”的问题串成的一门“大大”的学问。问有艺术、有技巧,“问”的优劣决定“效”的虚实。因此,课堂提问要注重实效。教师要立足“三问”来优化课堂提问,即问燃“激情”的火焰、问开“思维”的闸门、问亮“创新”的灯塔,从而切切实实地让学生的“学”乐起来、活起来、创起来。
一、何时问燃“激情”的火焰
激情是学习的启动器,是“乐学”之基。没有激情的学习,如同无盐的汤菜无味、无电的马达无力、无风的湖面泛不起涟漪。因此,教师应在问燃“激情”的火焰上动脑筋。
(一)问于学生“好玩”时
好玩是儿童的基本特征。数学课堂的“玩”,应该玩出门道、玩出花样。如二年级教材中“加减混合运算”的主题图显示:“地上有9只鸟,飞来6只,飞走4只。”这一静态的图,难以显示动态的飞。是先“飞来”还是先“飞走”,直接决定了列式的形式和计算的顺序。怎么办?问一问学生想不想“玩”。为了引导学生有目的地“玩”,教师先用屏幕显示“飞来”与“飞走”的情境,然后让学生表演。他们戴着头饰,听着配音:地上有9只鸟,飞来6只鸟,飞走4只鸟。学生听完后都会很快列出算式9+6-4。再让学生表演先“飞走”再“飞来”的情况,学生就会明白这种情况下应该先减后加,算式为9-4+6。这样变“图”为“演”,大大激发了学生探究的热情。
(二)问于学生“好动”时
好动是儿童的普遍特征。数学课堂的“动”,应该动出意义、动出水平。如教学一年级“9的分解和组成”时,如果采取教师讲学生听、教师摆学生看的方式,那知识是强加的,学生也会感到乏味。怎么办?问一问学生想不想“动”。这里的“动”不能随心所欲,而要满足两个条件:①既不重复又不遗漏;②减少操作的次数。在教师的带动下,学生“好动”的心理得到了满足,于是,他们充满热情地“动”起来:先将9根小棒一起放在左边,再依次从左边拿出1根、2根、3根、4根放到右边。学生一边叙述“9可以分成1和8,2和7,3和6,4和5”,一边联想“9可以分成8和1,7和2,6和3,5和4”。学生带着问题、动着脑筋在操作中叙述,在叙述中联想,在联想中发现,不仅动出了激情,而且动出了价值。
(三)问于学生“好奇”时
好奇是儿童的典型特征。数学课堂的“好奇”,不是追求刁钻的离奇,也不是追求古怪的离谱,而应该是刨根问底的一种欲望、打破砂锅问到底的一股劲头。如学习五年级“分数的再认识”时,可借故事诱发学生的好奇心:“在一个炎热的夏天,悟空和八戒分吃西瓜,悟空吃了一个西瓜四份中的一份,八戒吃了另一个西瓜四份中的一份。可是,八戒却抱怨自己吃得少,悟空吃得多。于是,他俩找师父来评理。同学们,你们知道唐僧是如何进行正确的评判的吗?”问题一抛出,学生的好奇之心瞬间被点燃,个个找理由,人人寻原因,争当唐僧来评判。
(四)问于学生“好胜”时
好胜是儿童的突出特征。数学课堂的“好胜”,不是好高骛远,也不是好大喜功,而应该是在压力面前争强、在困难面前要强。如教学“乘法分配律”,一开始就可以分组进行计算比赛,甲组计算136×4+64×4,乙组计算(136+64)×4。当乙组全部完成后,甲组大部分同学都没算出来。当教师宣布“乙组获胜”时,甲组的同学一个个噘着嘴:“不公平,乙组的题目简单些。”教师说:“不对呀,两组题中的数字相同,得数也相同!”“乙组题的计算步骤少一步。”甲组同学不服气地争辩,“乙组题可以口算得出答案。”甲组同学的“申诉”,已经触及乘法分配律的变化形式和运用价值。教师趁机引入“配套服装”“配套桌椅”的生活实例,让学生继续带着一颗好胜的心,为拼输赢而奋力探究。
二、何处问开“思维”的闸门
思维是数学的发动器,是“活学”之根。脱离思维的学习,犹如失线的风筝没有方向、断源的渠水失去活力、折翅的雄鹰无法飞翔。因此,教师应在问开“思维”的闸门上想办法。
(一)问于“观察”的联系处
观察,是发现的前提。观察之于数学学习,如同阳光、空气、水分之于植物一样。教师引导学生观察时,需要提供观察的源、选准观察的点、确定观察的序。如教学二年级“9的乘法口诀”,在呈现算式、提炼口诀后,让学生围绕“怎样才能记住口诀”进行观察,寻找算式与口诀之间的外部特征和内部联系。经过一番观察,有的发现积的十位上和个位上的数字相加的和都是9,如三九二十七,2+7=9;有的发现积的十位上的数总比口诀里第一个数少1,如五九四十五,4比5少1;有的发现从“一九得九”开始,下一句积的十位上数依次加1,个位上数依次减1,如一九得九、二九十八、三九二十七;有的发现几个九就比几十少几,如一九就比1个十少1,二九就比2个十少2……这些细心的发现,把9的乘法算式和口诀间的内在联系揭示得淋漓尽致。
(二)问于“比较”的疑难处
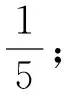
(三)问于“抽象”的转折处
抽象,是思维的方式。抽象要有现实的材料。小学数学中,许多概念是从现实原型中抽象出来的。教师引导学生抽象时,需要紧扣知识的本质,遵循认知的规律,把握抽象的时机。如二年级“认识角”,内容看似简单容易,实则高度抽象。教学时,师生需要共同参与找角、指角、折角、摸角、描角、创造角、比较角等多项活动,在活动中逐步抽象角的本质特征,且教师要及时提出恰当的问题引导学生思考,这样角的具体形象才会深深地烙印在学生的脑海中。如在学生折角后,让学生用折出来的角对着手心戳一戳,再摸一摸两边,问学生有什么感觉(尖尖的、平平的)。教师在黑板上描角时,提醒学生观察老师是从哪里开始描的、描了几次(从点开始描的、描了两次)。这样学生对角有一个尖尖的顶点和两条直直的边就有了深刻的印象。
(四)问于“概括”的关键处

三、何以问亮“创新”的灯塔
创新是发展的加速器,是“创学”之本。没有创新的学习,似断了横档的长梯,无法攀上无限风光的险峰;似丢失密码的门锁,无法打开未知领域的宝库;似船底漏水的小舟,无法通往精彩纷呈的彼岸。因此,教师应在问亮“创新”的灯塔上做文章。
(一)问于“具体—抽象”的实践中
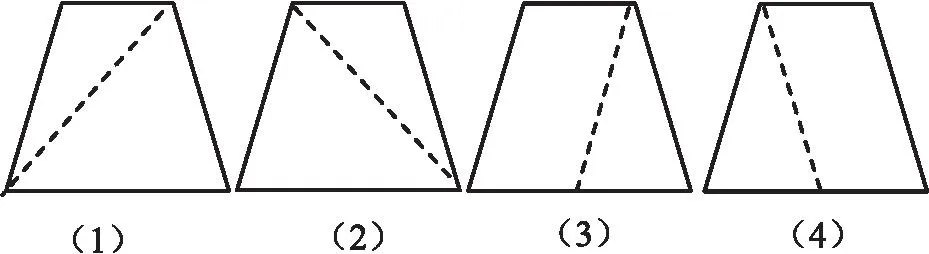
实践,是化具体为抽象的敲门砖。有效的实践需要大胆地试、自主地思。教学中,教师要以问题为导向,促使学生围绕求索的材料,在试中思、思中试,手脑并用,动思结合。如教学五年级“梯形的面积”,直接出示梯形(右图),开门见山地提问:“你能求出梯形的面积吗?”学生开始第一次“试”:分割梯形图形。
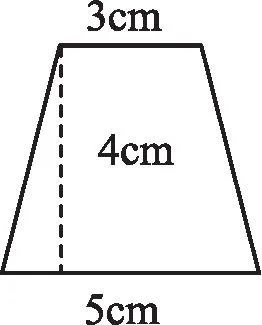
引导学生比较异同后,开始第二次“试”:计算梯形的面积。图(1)(2):3×4÷2+5×4÷2。图(3)(4):3×4+(5-3)×4÷2。学生凭借“试”,求出了面积,一个个脸上露出了笑容。教师趁热打铁:“能像长方形、正方形、平行四边形、三角形那样,直接计算面积吗?”基于此问,学生开始第三次“试”:操作推导公式。学生推导的方法五花八门,但结论殊途同归:S=(a+b)×h÷2。抽象出事物的本质后,回应课始追问:“分割计算与公式计算之间是否存在联系?”学生开始第四次“试”:寻找内在联系。图(1)(2)和图(3)(4)面积计算公式通过变形都可以转化为(3+5)×4÷2。学生通过四“试”,发现数学竟如此的神奇。
(二)问于“复杂—简单”的想象中
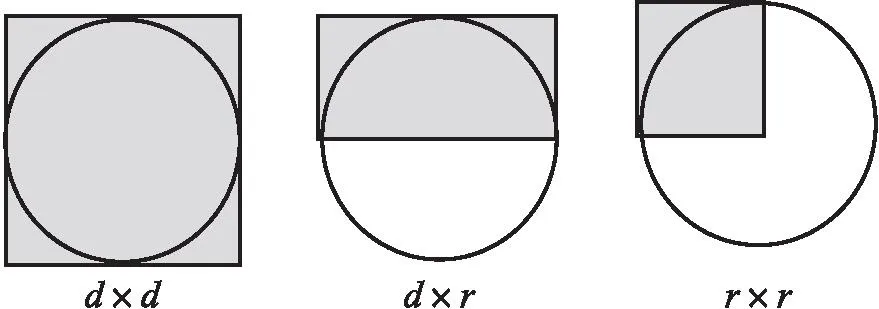
想象,是化复杂为简单的纽带。合理的想象需要大胆地猜想、科学地验证、合理地修正。教学中,教师要鼓励学生在“猜想—验证—修正”的循环中,透过复杂的表象去寻求简单的本质。如六年级“圆的面积”,它是小学几何初级知识难中之难,其原因有三:一是难以想到化曲为直,化圆为方;二是难以想象无穷无尽的极限表象;三是难以准确等分拼摆。因此,教师要耐心地围绕“猜想—验证—修正”来展开教学。①猜想:圆的面积计算公式可能是怎样的?学生受直线围成的图形的面积计算方法的干扰,往往会猜想c×c、c×d、c×r、d×d、d×r、r×r。②验证:依据猜想,画图验证,筛选出d×d、d×r和r×r。
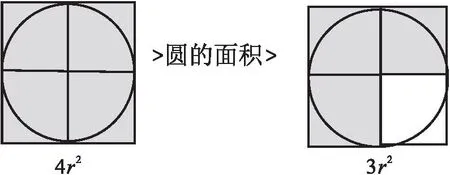
③修正:圆的面积在3r2与4r2之间。
④再猜想:3与4之间,有可能是π。因此,圆的面积可能是πr2。⑤再验证:学生操作学具,验证修正后的猜想。教师运用多媒体,展现“化曲为直,化圆为方”的过程。“哇!我们的猜想与科学的结论完全一致。”学生沉浸在成功的喜悦之中。
(三)问于“单一—多样”的发散中
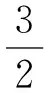
(四)问于“一般—特殊”的求异中