由一道中考压轴题联想到的“最值”求解策略

⦿ 江苏省苏州市苏州大学实验学校 李居先

“最值问题”是近年来中考数学的必考题型,也是压轴题中的必选之题.遇到此类问题,学生往往无从下手,掌握此类常见问题的解题策略会更容易找到问题突破口,便于解题.本文中将从巧用“配方法”“判别式”“公理”“函数”“平移”“模型” “旋转”“构造”“分割”等对一些特殊式子或线段(和或差)的最值问题进行剖析.

例如,2023年连云港市中考数学试题中的一道填空题:若W=5x2-4xy+y2-2y+8x+3(x,y为实数),求W的最小值.

分析此问题,显然常规解法不能完成解答,对于含有两个未知数的代数式最值问题,需要对代数式进行变形,将各个单项式之间的联系转化为完全平方式,再利用配方法把原式整理为“平方+常数”的形式,这样就可以确定此代数式的最值.故W=5x2-4xy+y2-2y+8x+3=(4x2-4xy+y2)-2y+x2+8x+3=(2x-y+1)2+(x+2)2-2.因为x,y均为实数,所以(2x-y+1)2≥0,(x+2)2≥0,故W≥-2,即W的最小值为-2.

当然,求解最值问题并不是只有简单的代数式的转化,还有更多的方法可以利用,下面就针对初中阶段“最值问题”的解法进行系统归纳,便于大家学习利用.

1 巧用“判别式”求代数式的最值

对于上述类型的代数式,可以利用其特点将代数式合理分配形成“完全平方式”再转化为“平方+常数”的形式求解,如上述解析过程.

研析：此类问题可以利用代数式与方程之间的内在联系,转化为方程,再利用判别式判断其最值问题.

解法如下:由题意,得5x2+(8-4y)x+y2-2y+3-W=0.因为x为实数,所以Δ=(8-4y)2-20(y2-2y+3-W)≥0,则5W≥(y+3)2-10≥-10,于是W≥-2.故W的最小值为-2.

2 巧用“公理”求线段最值

常见的最值问题往往体现在“两点之间线段最短”“垂线段最短”“三角形三边之间的关系”等方面,巧妙利用这些公理性质可破解最小值问题.

例1如图1,在矩形ABCD中,AB=5,BC=12,E为BC上一点,连接DE,将△CDE沿DE折叠,点C落在C′处,连接AC′,若F,G分别是AC′,AB的中点,求FG的最小值.

图1

研析：根据已知条件,如图2所示作辅助线,由勾股定理和折叠的性质可求得BD=13,CD=C′D=5.由三角形的三边关系,得C′B>BD-C′D.根据两点之间线段最短,则当点C′在DB上时,C′B的最小值为BD-C′D=8,由三角形的中位线定理求解.

图2

3 巧用“函数”求坐标系中动点间距离的最值

例2如图3,在平面直角坐标系中,二次函数y=-x2+2x-c的图象与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C.二次函数图象的对称轴与直线AC:y=x+3交于点D,若M是直线AC上方抛物线上的一个动点,求△MCD面积的最大值.

图3

研析：如图4,作MQ⊥AC于点Q,作ME⊥AB于点F,交AC于点E,先求出抛物线的对称轴,进而求得点C,D坐标及CD的长,从而得出过点M的直线y=x+m与抛物线相切时,△MCD的面积最大.根据x+m=-x2-2x+3的Δ=0求得m的值,进而求得点M的坐标,再求得CD上的高MQ的值,即可得出结果.

图4

4 巧用“平移”求相离线段和的最值

在遇到几何线段没有相互连接时,求其和的最值往往在问题的基础上利用平移作辅助线,让相离的线段连接在一起,然后再利用相关公理或者性质求解.

例3如图5,线段AC与BD相交于点E,连接AD,BC,若AC=3,BD=2,∠BEC=60°,求AD+BC的最小值.

图5

图6

5 巧用“模型”求线段和(差)的最值

求线段和(差)的最值的问题,常常用到“将军饮马”“隐圆”等模型,结合已知条件,将问题先转化为某种“模型”再来解得相关问题,化难为易.

例4如图7,正方形ABCD的边长是6,E是AD边上一动点,连接BE,过点A作AF⊥BE于点F,P是AD边上另一动点,求PC+PF的最小值.

图7

研析：如图8,取点C关于直线DA的对称点C′.以AB中点O为圆心,OA为半径画半圆.连接OC′交DA于点P,交半圆O于点F.

图8

6 巧用“旋转”求多条线段和的最值

此类问题实质上就是“费马点”问题,它是到三角形ABC三个顶点的距离之和最小的点P,即求PA+PB+PC的最小值.遇到此类形式的问题,我们通常考虑将某三角形旋转60°,将三条线段转化到同一条直线上,再利用两点之间的直线段最短进行判断,从而突破最值问题.

例5如图9,P是△ABC内的一点,连接PA,PB,PC,试求PA+PB+PC的最小值.

图9

研析：如图10,将△APC绕点A逆时针旋转60°到△AP′C′,则可以构造出等边三角形APP′,从而得到AP=PP′,CP=C′P′,于是将PA+PB+PC的值转化为PP′+PB+P′C′的值,则线段BC′的长即为所求的最小值.

7 巧用“构造”求“PA+k·PB”型线段的最值

此种类型问题是“PA+PB”最值问题的拓展,涉及的相关内容是“阿氏圆”问题,通常以动点P的运动轨迹来分类,一般分为两类,即点P在直线上运动和点P在圆上运动.

例6如图11,⊙O的半径为r,点A,B都在⊙O外,P为⊙O上一动点,已知r=k·OB,连接PA,PB,则当PA+k·PB的值最小时,点P的位置如何确定?

图11

研析：如图12,在线段OB上截取OC,使OC=k·r,则可证明△BPO∽△PCO,即k·PB=PC.故求PA+k·PB的最小值可以转化为求PA+PC的最小值.因为A,C为定点,P为动点,所以当点P,A,C共线时,PA+PC的值最小.

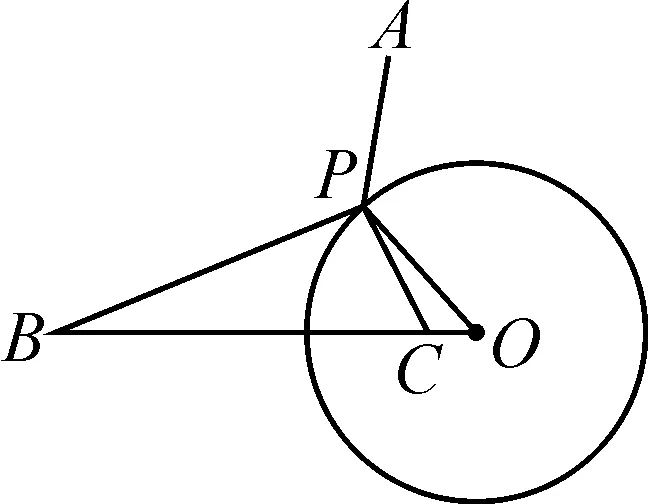
图12

综上所述,只有熟练把握不同形式的最值问题,搞清楚其中的关系,采用相对应的突破策略,才能化难为易.把握解决问题的策略,不仅仅是数学新课程标准的要求,更是课程改革在数学学科的一种能力体现.不断探索有效的解题方法与策略,开拓学生解题思维,有利于全面提升学生数学综合素养.