巧设问题,点燃思维活力

⦿ 江苏省苏州文昌实验中学校 谢裕恬

新课程改革的推进逐渐改变了课堂教学的模式、内容和方法,新的教学理念要求教师转变传统观念,成为课堂教学的引导者和组织者,落实学生的主体地位.教师在教学中要鼓励学生主动参与学习活动,在实践操作、合作探究、师生交流中获得知识和技能的提升.而课堂问题是联系师生思维活动的纽带,是点燃学生思维活力的钥匙.巧妙的问题设计能够加强师生之间的有效沟通交流,促进学生思维的发展,驱动学生有效完成自主探究活动,使教学活动有效开展.本文中从问题设计的角度,探析在教学中精心设计问题,促进学生发展的教学策略.

1 巧设问题,激发学习兴趣

兴趣是激发学生主动学习的动力,是点燃思维的火花.有效的问题能够驱动学生主动进行探索,激活学生的思维,趣味性的提问能够吸引学生的注意力,引导学生从不同的角度思考问题,从而不知不觉地进入自主学习状态,大大提高学习效率.

案例1有理数的乘方

师:同学们,我手中的这张纸厚度大约0.1 mm,现在将这张纸对折一次,请问厚度大约是多少?对折两次、三次呢?

生1:对折一次为0.2 mm,对折两次为0.4 mm,对折三次为0.8 mm.

师:假设将这张纸对折30次,它的厚度是多少呢?请同学们估算一下.

生猜测:1 000 mm?100 m?

师:看来大家很难估算,事实上早就有人做过实验,将一张纸对折30次之后,纸张的厚度将会超过10座珠穆朗玛峰叠起来的高度.

生:一张纸能有这么厚啊……怎么计算的呢?

师:大家仔细观察纸张折叠之后,计算高度的算式,是否有什么特点呢?

…………

本案例中教师没有直接将乘方公式教给学生,而是以情境的创设进行导入,激起学生的好奇心,以问题激发学生的学习兴趣,引导学生进行探究.富有趣味性的情境立刻吸引了学生的注意力,从而在轻松愉快的氛围中开始探索新知.

2 巧设问题,培养创新思维

新课程理念强调培养学生的核心素养,注重考查学生的数学能力、应用意识和创新意识,要求题型更加具有开放性和探索性.因此,教师在课堂教学中要创设探究性和开放性的问题,为学生创造更加广阔的探索空间,促使学生在自主探究中实现创新思维的发展,掌握思考和学习的方法.

案例2一次函数

一位农民售卖若干粮食时,为了方便出售,他准备了一些零钱,按照市场价出售了一部分粮食之后,又调整了价格将剩余的粮食全部出售了.他备用的零钱和出售粮食所得的钱与售出的粮食数量形成的函数关系如图1所示.根据图象,你能获得哪些信息?

图1

学生经过讨论,得到了相应的结论,并说明了理由.

生:根据一次函数的图象可知备用零钱为5元,卖了30 kg粮食,一共收入了15元,开始出售的价格为0.5元/kg,调价之后为0.4元/kg.

师:很好.如图2,如果不知道一共出售了45 kg粮食,只知道降价出售时,以0.4元/kg的价格将粮食全部出售,你能算出这位农民一共带了多少粮食吗?

图2

(经过上一问的引导式思考,学生根据函数图象能较轻松地解答,并讲解得出各项数据的理由.)

教师在课堂教学中不仅是知识的传播者,还要能够挖掘学生的潜能,发现学生的优点,使学生在学习过程中体会成就感,增强学习的信心.本案例中,教师在讲解一次函数问题时没有让学生直接就题解题,而是设计问题,让学生根据题目思考可以解决怎样的问题.教师以一道试题引导学生从不同的角度进行正向和逆向思维的思考,深度理解函数知识.同时,注重问题的开放性,没有设计具体的未知量,而是以连续的追问引导学生进行思考,挖掘潜能,激活思维.

3 巧设问题,提升学习能力

学习能力的提升是学生全面发展、终身学习的基础.学生的学习能力不仅体现在掌握的知识内容上,更体现在是否具备自主探索、自主思考的能力.教师在教学过程中要从学生的认知心理出发,设计符合学生心理特点和认知规律的问题,引导学生积极参与到学习活动中,并在讨论合作中深化学生的认识,启发学生探究知识本质,掌握规律,最终从被动学习转变为主动探究学习,实现学习能力的提升.

案例3解分式方程

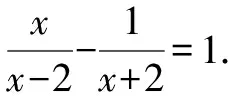
学生在解这道题的过程中进行了一系列的探讨,出现了如下多种解法.

解法1:原方程化为x(x+2)-(x-2)=x2-4.

解得x=-6.

经检验,x=-6是原方程的解.

解法2:原方程可化为

x2+2x-x+2=(x-2)(x+2),

x2+2x-x+2=x2+2x-2x-4,

x=-4-2-2.

解得x=-8.

经检验,x=-8是原方程的解.

解法3:原方程可化为

解得x=1.5.

经检验,x=1.5是原方程的解.

解法4:原方程可化为

x+1=x-2,0=-3.

所以,原方程无解.

解法5:原方程可化为

x+2=-4.

解得x=-2.

经检验,x=-2为增根,故原方程无解.

解法6:原方程可化为

x2+2x-x+2=x2-4.

解得x=-6.

所以x=-6是原方程的解.

教师将学生的不同解法一一展示,请学生分析哪种解法是错误的,并说出错误的理由.

生1:将x=-6代入原方程可使方程成立,因此解法1和解法6是正确的.

生2:解法2在合并同类项时出现了错误,多了“-2”,因此答案错误.

生3:解法3出现了通分错误.

生4:解法4在去分母时,没有在等式两边同乘一个不为零的整式,因此,答案也是错误的.

生5:解法5在通分时出现了计算错误.

师:同学们观察得非常仔细!在解方程的过程中会出现各种各样的错误,可能在约分时犯错,也可能在找最简公分母时出错,在去括号、移项等都可能出错.因此,根据以上的分析,解分式方程的步骤可归纳如下:

第一步,准确寻找最简公分母,在方程两边同乘最简公分母,从而将分式方程转化为整式方程.

第二步,要按照运算规则去括号,去括号时注意符号的正确性.

第三步,移项与合并同类项,注意符号的变化.

第四步,将分式方程转化为ax=b的形式.

第五步,将x的系数变为1,化成x=a的形式.

第六步,将方程的解代入原方程进行检验.

在教学过程中,教师还需要关注学生的反应,在学生遇到困惑和思路偏差时,及时予以引导,启发思维,激发智慧,让学生能够运用已有知识经验,发现和解决问题,在思考辨析中进行归纳总结,形成结构化的知识体系和解题方法,从而提升学习能力.本案例中,教师以辨析错误的方式,让学生转变角色,由学生自己分析错误并说明理由,使学生真正成为学习的主人.这样一来,不仅提升了他们辨析知识的能力,还增强了学习的信心.

综上所述,问题是知识的载体,有效的问题设计能够驱动学生进行主动探究和学习.教师要研究课标要求和学生情况,依托教学内容与学情设计问题,提高问题的质量.在课堂教学中巧妙设计问题,创设教学情境,能够帮助学生体验知识发展过程,强化对知识的理解,体会数学思想方法,拓展视野,提高学习效率,从而落实学生的主体地位,提高学习质量.