RV 减速器摆线轮齿廓修形对温度的影响

史瑞杰，郑鹏，张宏毅

（1.沈阳工业大学机械工程学院，辽宁沈阳 110870；2.沈阳航天三菱汽车发动机制造有限公司，辽宁沈阳 110179）

0 前言

随着工业自动化的不断发展，机器人技术已成为现代制造业的重要支柱。RV 减速器作为机器人关节的关键部件，其性能和可靠性对机器人的工作效率具有重要影响。然而，由于RV 减速器的高输入转速和降速比，热效应问题成为制约其性能的重要因素之一，因此对RV 减速器进行热分析具有重要的理论和工程实际意义。摆线齿轮是RV 减速器的核心部件之一，摆线齿轮的温度场分析对于提高RV 减速器的传动效率和可靠性具有重要意义。

在实际生产中，为了补偿摆线针轮传动的制造误差、便于拆卸和安装，同时改善润滑情况和增加传动效率，需要对摆线齿轮进行修形处理［1］。何卫东等［2］分析了摆线轮齿廓修形对回差的影响，并建立数学模型；孙章栋等［3］研究了摆线轮组合修形方式对摩擦润滑特性规律的影响；陈馨雯等［4］研究了摆线轮修形对接触受力和传动误差的影响；乔雪涛等［5］对摆线轮修形对传动精度的影响进行探讨。目前对于摆线轮修形问题的影响研究较为广泛，但摆线轮修形方式对温度影响的研究却鲜有提及。因此，本文作者通过理论计算与仿真分析，探究摆线轮修形对温度的影响规律，研究结果为摆线轮的温度场问题和修形设计提供一定的指导意义。

1 摆线轮瞬时摩擦热

RV 减速器是二级减速器，结构如图1 所示。摆线齿轮与针齿啮合过程中会产生接触压力和相对滑动，滑动过程中因摩擦产生的热量被摆线齿轮和针齿吸收形成相应的升温，有可能使传动机构发生热变形、产生热胶合进而降低传动精度。

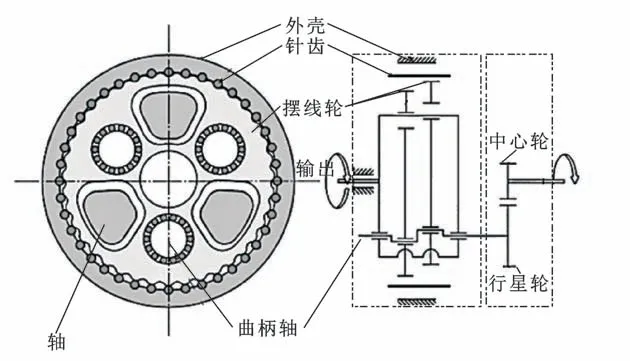
图1 RV-E 系列减速器结构Fig.1 Structure of RV-E series reducer

摆线齿轮与针齿啮合过程中产生的瞬时摩擦热量计算公式为

式中：σH为齿面的接触应力；vr为轮齿和针齿之间的相对滑动速度；f为轮齿和针齿间的摩擦因数［6］；γ为能量转换系数，一般取0.9～0.95 之间。

1.1 平均接触应力的计算

摆线齿轮与针齿的接触瞬间可以看作是两圆柱体间的接触，接触情况符合赫兹接触，且摆线齿轮和针齿的材料均为GCr15，因此可以使用简化后赫兹公式来计算最大接触应力，平均接触应力为其最大接触应力的π／4 倍［7］。计算公式如下：

式中：ρei为当量曲率半径；Fi为法向接触压力；b为齿宽；E为弹性模量，取2.06×105MPa。

1.1.1 当量曲率半径的计算

摆线齿轮曲率半径可由以下公式求得：

式中：φi为啮合相位角；K为短幅系数，按照下式计算：

针齿与摆线轮的啮合点的当量曲率半径为

1.1.2 法向接触压力的计算

（1）标准齿廓接触压力的计算

摆线齿轮传动中受力情况如图2 所示，齿轮在转矩的驱动下运动，有一半的轮齿参与啮合，每个啮合齿上的瞬时压力的作用方向均为瞬心［8］。

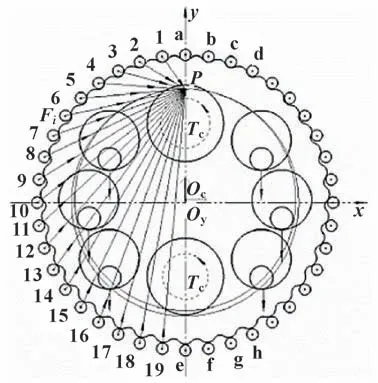
图2 摆线轮受力简图Fig.2 Stress diagram of cycloid wheel

齿廓受力计算公式如下：

式中：Tc为单片摆线轮输出转矩，因减速器为两片摆线轮，所以可以近似由Tc＝0.55T进行计算。

（2）修形齿廓接触压力的计算

本文作者以某型号RV-E 系列减速器为研究对象，其相关参数见表1。

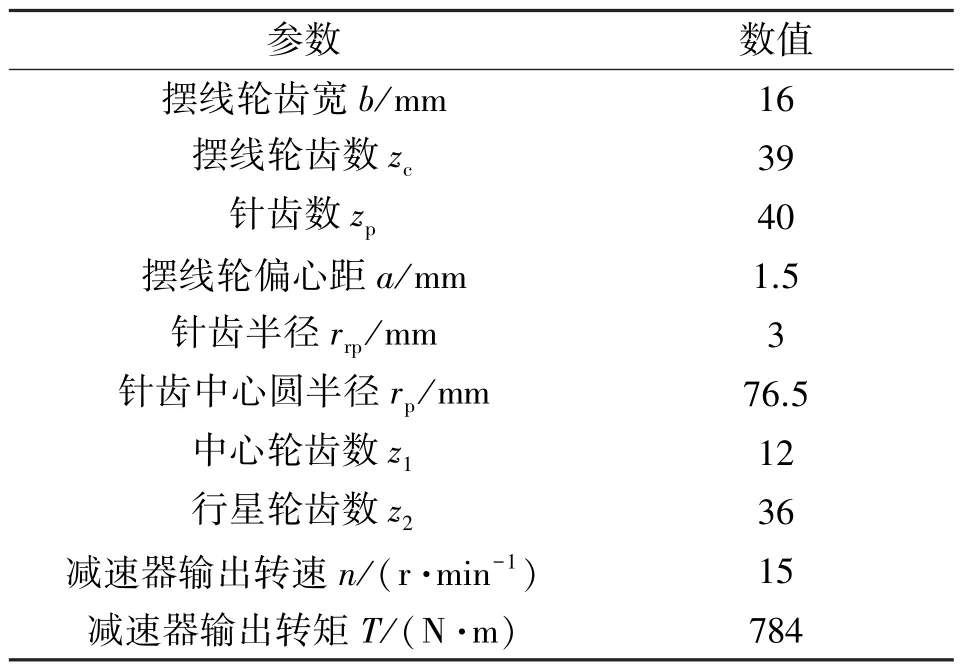
表1 减速器相关参数Tab.1 Relevant parameters of reducer

在实际工作中，摆线轮齿廓修形一般采用等距＋移距的组合修形方式。因负等距＋负移距无法生成合理啮合间隙，故修形多采用正等距＋负移距、负等距＋正移距、正等距＋正移距3 种组合修形方式［9］。给定相同的径向间隙Δ＝0.006 mm，按照文献［10］中的方法得到3 种修形方式的最佳修形量如表2 所示。

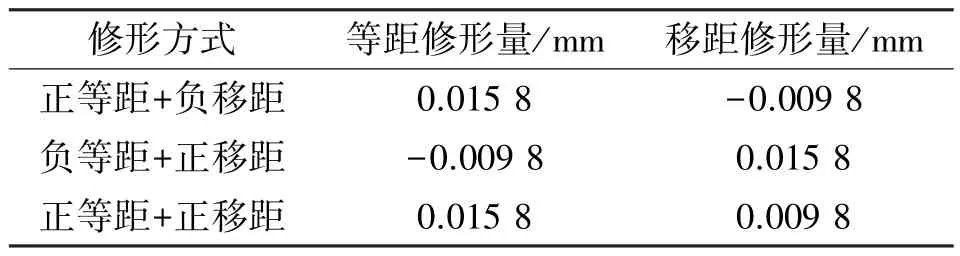
表2 最佳修形量Tab.2 Optimal modification amounts

修形齿廓与针齿啮合时，不再是无间隙的啮合，初始状态下只有一对轮齿啮合［11］，其余轮齿与针齿之间存在初始啮合间隙，计算方式如下：

式中：Δrrp为等距修形量；Δrp为移距修形量。

3 种组合修形方式的初始啮合间隙如图3 所示。

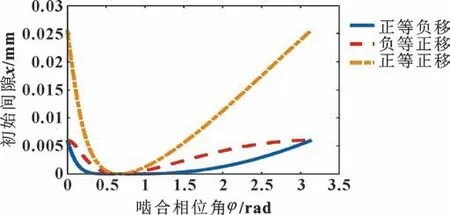
图3 初始啮合间隙Fig.3 Initial engagement clearances

修形齿廓传动中第i个齿的受力可以表示为

式中：δi为各啮合点的总变形量；δmax为受力最大的一对轮齿的变形量；Fmax为最大受力。各参数计算方式如下：

式中：fmax为受力最大齿与针齿销的弯曲变形量，变形量小可以忽略［12］；wmax为受力最大齿与针齿的接触变形量；m为第m齿开始啮合；n为第n齿结束啮合；μ为泊松比0.3；E为弹性模量2.06×105MPa；rc为摆线轮的节圆半径，rc＝azc。

当传递转矩时，轮齿与针齿之间的总变形量大于初始啮合间隙时，轮齿与针齿发生啮合［13］，否则不会啮合，这两条曲线产生两个交点对应两个啮合相位角，处于这两个啮合相位角之间的轮齿都处于啮合状态。

因为计算Fmax时需要δmax的数值，而计算δmax时又需要Fmax的数值，所以需要给出一个初始的Fmax的数值，由Fmax0开始迭代，计算公式如下：

综上所述，Fmax的迭代流程如图4 所示。

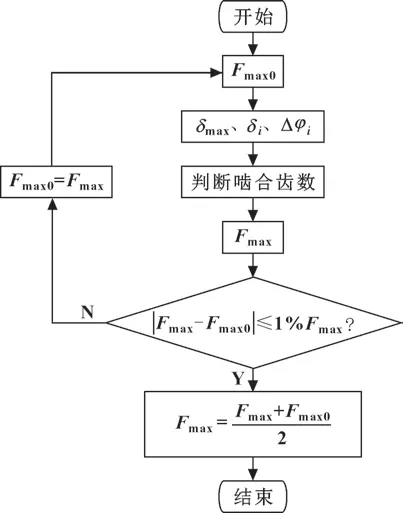
图4 迭代流程Fig.4 Iteration flow

整合以上数据并代入公式（2）中可以得到标准齿廓与修形齿廓所受的应力如图5 所示。随着啮合范围的减小，轮齿所受压力与应力增大，修形前后应力最大位置随啮合范围的减小而前移。

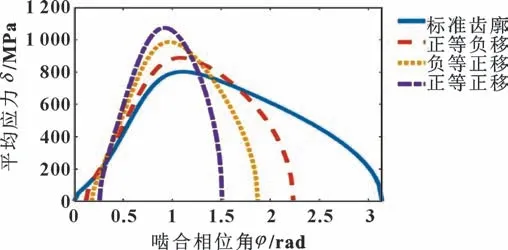
图5 应力对比Fig.5 Stress comparison

1.2 相对滑动速度的计算

此次分析针齿固定且无针套的相对滑动速度，计算公式［14］如下：

式中：ωH、nH分别为摆线针轮传动机构的输入轴的角速度和转速。

1.3 摩擦因数的计算

摩擦因数的数值与多种因素相关，可由下式计算不同啮合位置的摩擦因数：

式中：x为啮合处的粗糙度因子；η为润滑油动力黏度；Fti为啮合处的切向载荷；vn为切向速度；s1、s2为齿轮与针齿的表面粗糙度；d为摆线轮的分度圆直径。

整合以上数据并代入公式（1）中进行计算，得出摆线齿轮与针齿啮合过程中的瞬时摩擦热的计算结果如图6 所示，摆线轮修形前后瞬时摩擦热量的最大数值基本一致，但峰值的位置会随着啮合范围的减小而发生前移。

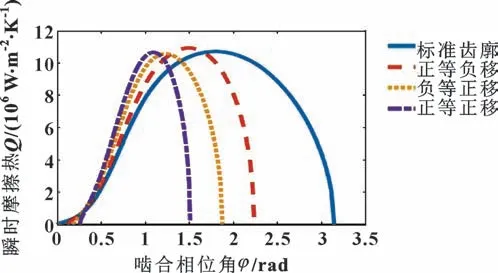
图6 瞬时热量对比Fig.6 Instantaneous heat comparison

2 啮合的周期性热量

摆线针轮传动机构工作过程中摩擦产生的热量分别传递给针齿和摆线齿轮，引入一个分配因子β进行热量分配。齿轮的瞬时摩擦热量可以表示为

摆线齿轮的轮齿与针齿的啮合是周期性的，所以热量在单个轮齿的产生也呈周期性变化，在计算摆线齿轮的稳态温度场时还需要把计算得出的瞬时摩擦热量平均分配到摆线齿轮轮齿的每一个啮合周期内。计算过程［7］如下：

式中：qi为不同啮合位置的热量；T为啮合周期；aH为接触面的半宽，由赫兹公式演化而来。

计算结果见图7，周期热量随着啮合范围的减小而增大，峰值位置仍处于同一啮合相位角上。

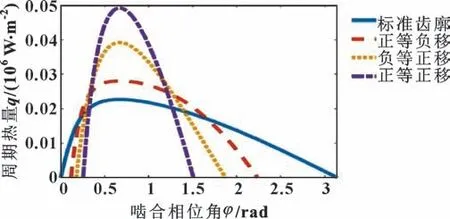
图7 周期热量对比Fig.7 Cycle heat comparison

3 齿轮表面对流换热

在摆线针轮传动机构工作过程中，产生的摩擦热量会传递给摆线齿轮和针齿，剩下的热量通过与润滑脂的对流散失。

齿轮齿面对流换热系数计算公式［15］：

齿轮端面对流换热系数计算公式：

式中：λ为导热率；ω为摆线轮自转角速度；ν为运动黏度；ρ为密度；c为比热容。

4 稳态温度场有限元分析

摆线齿轮在与针齿啮合的过程中产生摩擦热使得齿面齿轮温度上升，上升的温度传递给整个摆线齿轮和针齿，并通过对流散失一部分热量，最终整个齿轮的温度会趋于平衡达到一个稳定的状态，称为稳态温度。

在有限元分析软件中设置材料热传导系数为44 W／（m·℃），施加边界条件，设置环境温度为22 ℃并求解，计算得到的结果如图8 和图9 所示。

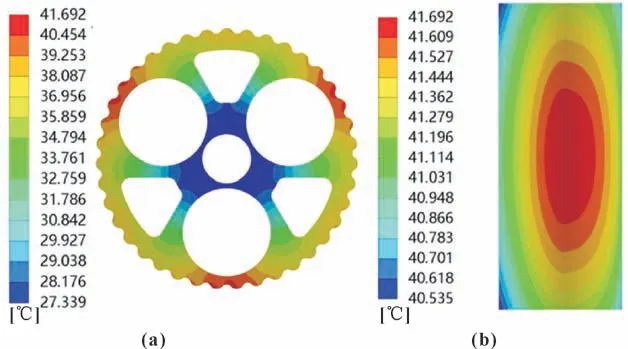
图8 标准齿廓整齿（a）及单齿（b）温度场Fig.8 Temperature fields of whole tooth（a）and single tooth（b）with standard tooth profile

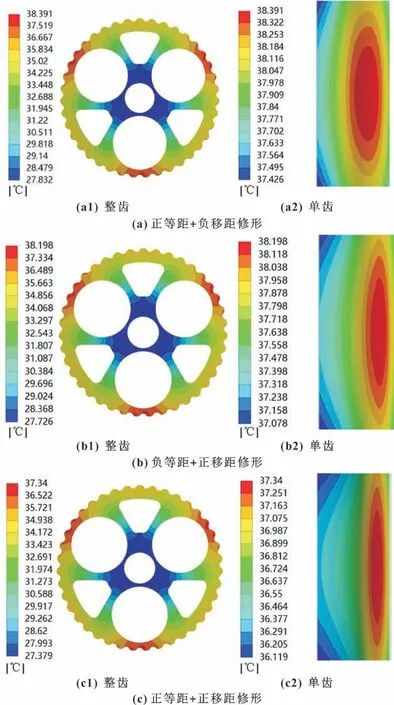
图9 修形齿廓整齿及单齿温度场Fig.9 Temperature fields of whole tooth and single tooth with modified tooth profile：（a）positive isometric＋negative displacement correction；（b）negative isometric＋positive displacement correction；（c）positive isometric＋positive displacement correction

从图9 可以看出：热量沿齿宽方向呈现对称分布，沿径向分布梯度变化较大，啮合区域温度明显高于非啮合区域。达到稳态以后齿轮的最高温度为41.7 ℃。

修形齿廓温度分布规律与标准齿廓大致相同，3种组合修形方式均可以使摆线轮稳态温度降低。降温效果由小到大分别为正等距＋负移距、负等距＋正移距、正等距＋正移距。由于修形后齿轮的啮合范围减小，在温度场的温度分布相较于标准齿廓更加集中，啮合处的温度梯度的密集程度随着啮合范围的减小而增加。

5 结束语

本文作者在假定针齿与针齿套不产生相对滑动的前提下，通过对摆线齿轮的标准齿廓以及组合修形后的齿廓分别计算并进行对比分析，结论如下：

（1）3 种组合修形方式产生的初始啮合间隙中，正等距＋正移距修形产生的啮合间隙远大于其余两种修形方式，润滑空间更大。

（2）齿轮修形前后啮合产生的瞬时摩擦热量最大值基本保持不变，峰值位置会发生变化；周期热量随啮合范围的减小而增大，且热量峰值集中于轮齿的相同啮合相位角上。

（3）摆线齿轮达到稳态温度后，温度沿齿宽方向呈对称分布。常用组合修形方式均可以减低齿轮温度，在相同径向间隙为0.006 mm 时，降温效果最佳的修形方式为正等距＋正移距修形。修形齿廓单齿温度的集中程度大于标准齿廓，且随啮合范围的减小而增大。