平面等距变换及其矩阵表示

胡永建 周 蓓

(北京师范大学数学科学学院 100875)

《普通高中数学课程标准(2017年版2020年修订)》将平面与空间等距变换列为普通高中数学选修课程A类课程“空间向量与代数”专题的教学内容. 通过该内容的学习，使学生了解平面与空间变换的定义，理解平面与空间等距变换，掌握常见平面与空间等距变换及其矩阵表示[1]．平面和空间等距变换对于高中数学教师来说，几乎都是全新的教学内容．本文首先介绍有关映射和变换的基本概念[2,3]，然后介绍平面等距变换的定义、性质和矩阵表示，最后通过例子介绍平面等距变换的矩阵表示的应用．希望本文的介绍对高中数学教师理解和讲授这部分内容有参考价值.

1 映射与变换

设σ为从集合X到Y的映射，如果存在从集合Y到X的映射τ，使得τσ=idX，στ=idY，则称σ为可逆映射．此时，τ称为σ的一个逆映射．事实上，如果σ是可逆映射，则它的逆映射是唯一的．我们将σ的逆映射记作σ-1.可以证明，σ为可逆映射当且仅当σ为双射．并且，如果σ，τ为可逆映射，则σ-1,τσ也是可逆映射.

集合X到自身的一个映射称为X的一个变换．所以，恒等映射也称为恒等变换. 设σ为集合X的一个变换，x∈X．如果σ(x)=x，则称x为σ的一个不动点．显然，X中的每一个元素都是恒等变换idX的不动点.

2 平面等距变换及其性质

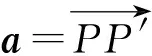
下面介绍平面等距变换的一些基本性质.

如果在性质1中限定t∈[0，1],那么线段AB在σ下的象为线段A′B′.因此，平面等距变换将线段变成与之等长的线段，进而将直线变成直线，将三角形和平行四边形分别变成与之全等的三角形和平行四边形．一般地，平面等距变换将每个平面图形变为大小和形状与之完全一样的图形.

性质2平面等距变换的乘积还是平面等距变换.

证明设σ，τ为平面等距变换．对平面内任意两点P,Q，令P′=τ(P)，Q′=τ(Q)，P″=σ(P′),Q″=σ(Q′),则P″=στ(P)，Q″=στ(Q)．由于σ，τ均为平面等距变换，故PQ=P′Q′，P′Q′=P″Q″，从而PQ=P″Q″．故στ是平面等距变换.

由性质2知，平面等距变换关于变换的乘积运算是封闭的.

性质3平面等距变换是可逆变换，且其逆变换也是平面等距变换.

上式表明，P′与P″重合，即P′为点P在σ之下的象．故σ又是满射．综上所述，σ是双射，从而是可逆变换，即σ-1存在．另外，对平面内任意两点S，T，令S′=σ-1(S)，T′=σ-1(T)，则S=σ(S′),T=σ(T′)．由于σ为等距变换，故ST=S′T′．因此，σ-1也是平面等距变换.

3 平面等距变换的矩阵表示

建立平面直角坐标系后，平面上的点P(x，y)与R2中的向量a=(x，y)T一一对应．于是，我们可以用R2表示平面，用列向量a=(x，y)T表示平面上的点P(x，y)．此时，每个平面变换均可唯一地表示成R2的变换的形式．并且，如果a，b∈R2分别表示平面上的点P,Q，则线段PQ的长恰好等于向量a-b的长度，即

这样一来，我们可以用代数方法研究平面等距变换.

首先，我们给出平面等距变换的一个分解．

引理1如果φ为平面等距变换，那么φ=τσ，其中τ是以v=φ(0)为平移向量的平移变换，σ是以0为不动点的平面等距变换．

证明设τ是以v=φ(0)为平移向量的平移变换，则τ为可逆变换．令σ=τ-1φ，则σ也是平面等距变换，且满足φ=τσ.由于τ(0)=v，故σ(0)=τ-1φ(0)=τ-1(v)=0．所以，σ是以0为不动点的平面等距变换.

引理1表明，每一个平面等距变换总可以分解为一个平移变换和一个以0为不动点的平面等距变换的乘积．下面，我们研究引理1中平面等距变换σ的性质.

引理2如果σ是以0为不动点的平面等距变换，那么σ保持向量的内积不变，即：对任意a，b∈R2，σ(a)·σ(b)=a·b.

证明由于σ为平面等距变换，故对任意a，b∈R2，都有|σ(a)-σ(b)|=|a-b|．选取b=0，可得|σ(a)|=|a|．于是，

|σ(a)-σ(b)|=|a-b|

⟹(σ(a)-σ(b))·(σ(a)-σ(b))

=(a-b)·(a-b)

⟹|σ(a)|2+|σ(b)|2—2σ(a)·σ(b)

=|a|2+|b|2-2a·b

⟹σ(a)·σ(b)=a·b.

故结论成立．

设σ为R2的一个变换．如果σ满足

(1)对任意a，b∈R2，

σ(a+b)=σ(a)+σ(b)；

(2)对任意k∈R，a∈R2，σ(ka)=kσ(a)，

则称σ为R2的一个线性变换．

引理3如果σ是以0为不动点的平面等距变换，那么σ是线性变换．

证明由引理2知，对任意a，b∈R2，

|σ(a+b)-σ(a)-σ(b)|2

=(σ(a+b)-σ(a)-σ(b))·(σ(a+b)

-σ(a)-σ(b))

=(a+b)·(a+b)-2(a+b)·a-2(a+b)·b+2a·b+a·a+b·b

=-(a+b)·(a+b)+2a·b+a·a

+b·b

=0.

故σ(a+b)=σ(a)+σ(b)．

另一方面，对任意k∈R，a∈R2，

|σ(ka)-kσ(a)|

=(σ(ka)-kσ(a))·(σ(ka)-kσ(a))

=(ka)·(ka)-2k(ka)·a+k2a·a=0．

故σ(ka)=kσ(a)．综上所述，σ是一个线性变换.

接下来，我们推导平面等距变换的矩阵表示.

ψ(a)=τσ(a)=σ(a)+v=xσ(e1)+yσ(e2)+v．

如果记ψ(a)=(x′，y′)T，则上式可以写成矩阵乘积的形式：

(1)

或者

(2)

反过来，设平面变换ψ由(1)或(2)给出．容易检验，对任意a，b∈R2，|ψ(a)-ψ(b)|=|a-b|．故ψ为平面等距变换.

因此，建立平面直角坐标系后，每一个平面等距变换均可唯一地表示成(1)或(2)的形式．我们称(1)和(2)为平面等距变换的矩阵表示．其中(1)式表示的平面等距变换ψ称为第Ⅰ型平面等距变换，(2)式表示的等距变换ψ称为第Ⅱ型平面等距变换．如果某个第Ⅰ型平面等距变换ψ有不动点P(x0，y0)，那么(1)式可改写为

(3)

此时，ψ为绕点P(x0，y0)逆时针旋转角θ的旋转变换．类似地，如果某个第Ⅱ型平面等距变换ψ有不动点P(x0，y0)，那么(2)式可改写为

此时，ψ为关于过点P(x0，y0)的直线sinθ(x-x0)-(1+cosθ)(y-y0)=0的反射变换．

特别地，当平移向量v=(0，0)T时，由(1)表示的第Ⅰ型平面等距变换ψ为绕原点逆时针旋转角θ的旋转变换；由(2)表示的第Ⅱ型平面等距变换ψ为关于过原点的直线xsinθ-y(1+cosθ)=0的反射变换．

4 应用举例

应用平面等距变换的矩阵表示，我们可以证明有关平面等距变换的一些有趣性质.

例1证明：第Ⅰ型平面等距变换为平移变换或旋转变换，第Ⅱ型平面等距变换为直线反射变换或平移变换与直线反射变换的乘积.

证明设ψ为第Ⅰ型平面等距变换，(1)为ψ的矩阵表示．当θ=2kπ(k∈Z)时，(1)式变为

(4)

此时，ψ为平移变换．当θ≠2kπ(k∈Z)时，二元一次方程组

有唯一解(x0，y0)T．容易检验，P(x0，y0)为ψ的不动点．此时，ψ为绕点P(x0，y0)逆时针旋转角θ的旋转变换.

再设ψ为第Ⅱ型平面等距变换，(2)为ψ的矩阵表示．当ψ有不动点P(x0，y0)时，由上一节最后的分析知，ψ为关于直线sinθ(x-x0)-(1+cosθ)(y-y0)=0的反射变换．当ψ没有不动点时，ψ是以v=(s，t)T为平移向量的平移变换与关于直线xsinθ-y(1+cosθ)=0的反射变换的乘积.

从例1的结果可以看出，每个平面等距变换要么是平移变换、旋转变换、直线反射变换之一，要么是平移变换与直线反射变换的乘积．所以，我们称平移变换、旋转变换、直线反射变换是三种基本的平面等距变换.

例2证明：每个平移变换和旋转变换总可表示为两个直线反射变换的乘积.

其中θ=2φ-π．容易检验，σ，τ均有不动点且στ的矩阵表示为(4)．因此，σ，τ为直线反射变换且ψ=στ.

再设ψ是绕点P(x0，y0)逆时针旋转角θ的旋转变换．则ψ的矩阵表示具有(3)的形式. 选取平面等距变换σ，τ，其矩阵表示分别为

则σ，τ分别为以P(x0，y0)为不动点的直线反射变换．容易检验，στ的矩阵表示恰好与ψ的矩阵表示相同．故ψ=στ．这表明，旋转变换ψ可以表示为两个直线反射变换的乘积．

从例1和例2可以看出，每个平面等距变换总可以表示为不超过3个直线反射变换的乘积．

例3设σ，τ分别为关于直线l1，l2的反射变换．证明：如果l1，l2平行，则στ为平移变换；如果l1，l2相交，则στ为绕交点的旋转变换.

证明当l1，l2平行时，建立平面直角坐标系，使得l1，l2的方程分别为y=a与y=0，则σ，τ的矩阵表示分别为

则στ的矩阵表示为(x′，y′)T=(x，y)T+(0，2a)T．故στ为以v=(0，2a)T为平移向量的平移变换.

当l1，l2相交时，以交点为原点，并以l2为横轴建立平面直角坐标系，那么σ，τ的矩阵表示分别具有下面的形式：

其中θ≠2kπ(k∈Z)．容易检验，στ的矩阵表示为

故στ为绕原点逆时针旋转角θ的旋转变换.

此外，利用平面等距变换的矩阵表示，我们也可以证明平面等距变换是可逆变换，以及有公共不动点的平面旋转变换与直线反射变换的乘积为直线反射变换.