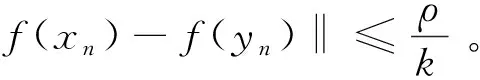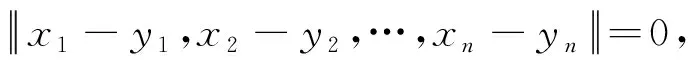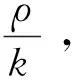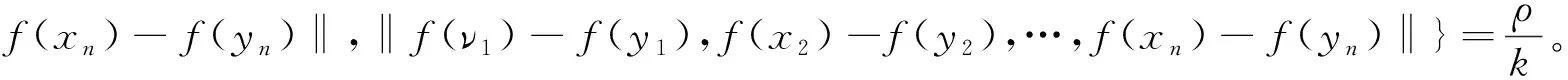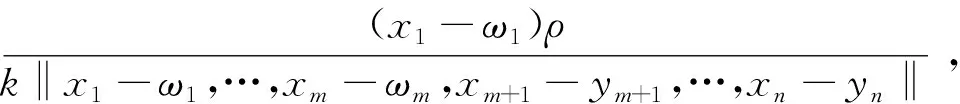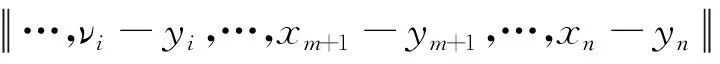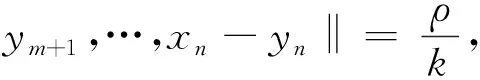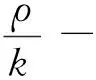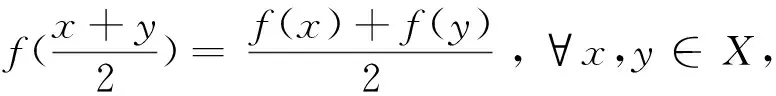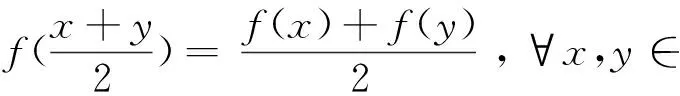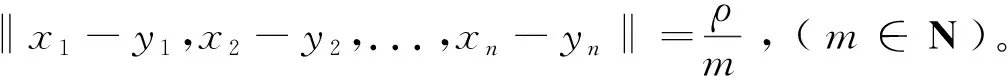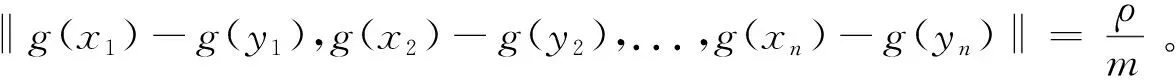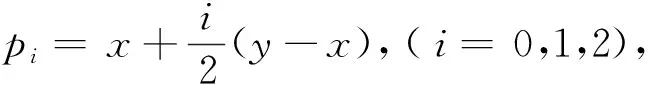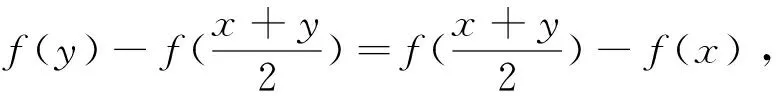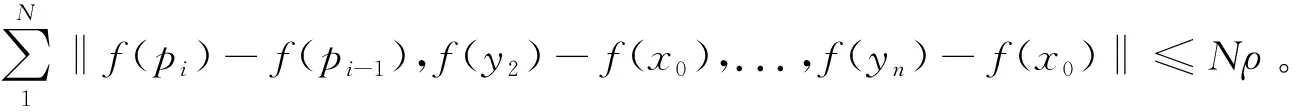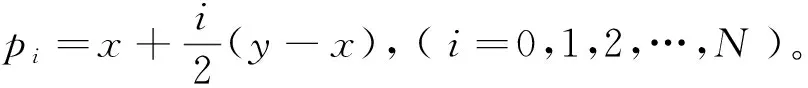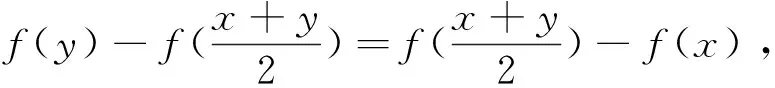n-赋范空间上的等距延拓问题

马玉梅

(大连民族大学 理学院， 辽宁 大连 116650)

等距理论在泛函分析以及数学的其它分支和物理学研究中具有重要意义，如万有定理(可分Banach 空间等距嵌入到C[0，1]的闭线性子空间)，W.T. Gowers 和 B. Maurey 给出无条件基可以等距嵌入到不同于l1和c0的Banach 空间。Grzegorz Lewicki证明Orlicz 空间可以等距嵌入到Lp-spaces等等[1]。几何学上基于流形的等距刻画了黎曼对称空间，黎曼对称空间的分析学为Hillel Furstenberg赢得2006年Wolf 奖[2]。

1 引言和术语

设X和Y是度量空间，称映射f:X→Y为等距映射，如果对任意x,y∈X有dX(x,y)=dY(f(x),f(y))。这里dX(·,·),dY(·,·)分别表示X与Y空间的度量。

1932年赋范空间:Mazur 和 Ulam给出：“满”等距算子必为仿射算子[3]。“非满”等距延拓为线性或仿射问题一直是80多年以来研究的热点。1987年J. Baker 得到严格凸空间的等距单映射必为仿射的[3]。

1970年Aleksandrov[4]提出：度量空间中保持单位距离的映射是否为等距映射。

针对这个问题的研究主要在两类空间展开。

(1)赋范空间。W. Benz 推广了Aleksandrov 问题， 给出了保持两个常数距离的映射为等距的条件[5]:

定理1 设X与Y为两个实线性赋范空间，Y是严格凸的。如果映射f:X→Y满足

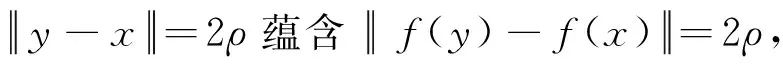
(2) n-赋范空间。2004年起，H. Chu， C. Park， T.M. Rassias，高金梅、任卫云、靖阳平等将Aleksandrov 问题推广到2-赋范和n-赋范空间[6-22]； C. Park 和 T.M. Rassias 给出了n-距离下满足n-DOPP，n-Lipschitz 以及保持m-colinear (m=2，n)等条件的映射是n-等距的。H. Gunawan 和 M. Mashadi 给出了范数降维理论，为进一步解决n-赋范空间中维数限定问题提供了重要依据。基于此理论马玉梅于2013年分别得到了n-赋范空间中保持单位距离且保持n-共线与2-线性保序的映射为弱n-等距的；n-赋范严格凸空间中强保持单位距离并且保持任意正整数的映射是n-等距的。

2014年马玉梅给出[18]:

定理2 设X，Y 是两实n-赋范线性空间，且dimX≥n，f:X→Y满足w-n-DOPP，那么以下8个命题等价:

(1) f 保持w-n-0-距离 (w-n-0-distance， n-colinear);

(2) f 是w-n-Lipschitz;

(3) f 保持2-共线(2-colinear);

(4) f 是仿射的(affine);

(5) f 是n-等距的(n-isometry);

(6) f 是n-Lipschitz;

(7) f 保持n-0-距离(n-0-distance);

(8) f 是弱-n-等距的(w-n-isometry)。

本文将赋范空间中的Benz定理推广到n-赋范空间。

2 n-赋范空间中的相关概念

定义1[6]设X 是实线性空间，dimX≥n，函数‖·,…,·‖:Xn→R满足:

(1)‖x1,…,xn‖=0,当且仅当x1,…,xn是线性相关的；

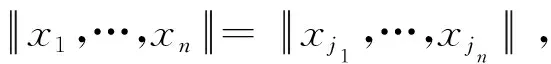
(3) ‖αx1,…,xn‖=|α|‖x1,…,xn‖；

(4) ‖x+y,x2,…,xn‖≤‖x,x2,…,xn‖+‖y,x2,…,xn‖。

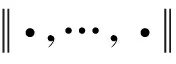
注释[6]:设X与Y是实n-赋范空间. 那么对所有x1,…,xi,…,xj,…,xn∈X。

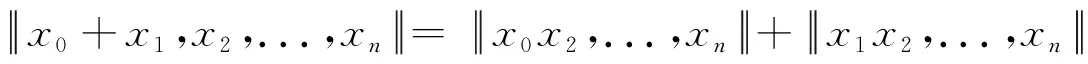
定义3[8]映射f:X→Y称为w-n-等距，如果：对任意x0,x1,…,xn∈X,

‖f(x1)-f(x0),…,f(xn)-f(x0)‖=‖x1-x0,…,xn-x0‖。

映射f:X→Y称为w-n-DOPP，如果：对任意x0,x1,…,xn∈X，

‖x1-x0,…,xn-x0‖=1 蕴含‖f(x1)-f(x0),…,f(xn)-f(x0)‖=1。

映射f:X→Y称为w-n-Lipschitz，如果：对任意x0,x1,…,xn∈X，

‖f(x1)-f(x0),…,f(xn)-f(x0)‖≤‖x1-x0,…,xn-x0‖。

映射f:X→Y称为n-等距，如果: 对任意x1,…,xn,y1,…,yn∈X，

‖f(x1)-f(y1),…,f(xn)-f(yn)‖=‖x1-y1,…,xn-yn‖。

映射f:X→Y称为n-ρ-距离， 如果：对任意x1,…,xn,y1,…,yn∈X，

‖x1-y1,…,xn-yn‖=ρ蕴含 ‖f(x1)-f(y1),…,f(xn)-f(yn)‖=ρ。

映射f:X→Y称为n-Lipschitz 如果: 对任意x1,…,xn,y1,…,yn∈X，

‖f(x1)-f(y1),…,f(xn)-f(yn)‖≤‖x1-y1,…,xn-yn‖。

映射f:X→Y称为保持2-共线的， 如果对于任何x,y,z∈X， 存在t∈R，满足z-x=t(y-x) 那么就存在s∈R，使得f(z)-f(x)=s(f(y)-f(x))。 点集x0,x1,…,xn∈X称为n-共线的，如果对每个i，{xj-xi:0≤j≠i≤n} 是线性相关的。映射f:X→Y称为保持n-共线的， 如果x0,x1,…,xn是n-共线的，则f(x0),f(x1),…,f(xn) 是n-共线的，n-共线的。

注释：映射f:X→Y保持n-共线意味f保持w-0-距离(‖x1-x0,…,xn-x0‖=0，蕴含‖f(x1)-f(x0),…,f(xn)-f(x0)‖=0)。

3 n-范空间中的Benz定理

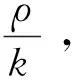
证明任取x1,…,xn,y1,…,yn∈X满足‖x1-y1,…,xn-yn‖=0，也即:x1-y1,…,xn-yn是线性相关的。 假设 {xm+1-ym+1,…,xn-yn} 是{x1-y1,…,xn-yn}的最大线性无关组(m

max{‖(ν1-x1)+(x1-y1),x2-y2,…,xn-yn‖,‖x1-y1,x2-y2,…,xn-yn‖}=

‖(ν1-x1)+(x1-y1),x2-y2,…,xn-yn||≤‖ν1-x1,x2-y2,…,xn-yn‖。我们得到：

xi-νi=ωi-xi，νi-yi=(xi-ωi)+(xi-yi)，i∈{2,3,…,m}。 由于xi-yi,xm+1-ym+1,…,xn-yn是线性相关的，我们有‖…,xi-yi,…,xm+1-ym+1,…,xn-yn‖=0,‖…,xi-ωi,…,xm+1-ym+1,…,xn-yn‖≤

max{‖…,(xi-ωi)+(xi-yi),…,xm+1-ym+1,…,xn-yn‖,‖…,xi-yi,…,xm+1-ym+1,…,xn-yn‖}≤

max{‖…,xi-ωi,…,xm+1-ym+1,…,xn-yn‖,‖…,xi-yi,…,xm+1-ym+1,…,xn-yn‖},

‖ν1-y1,…,xm+1-ym+1,…,xn-yn‖=‖ν1-x1,…,xm+1-ym+1,…,xn-yn‖。

由于f保持ρ/(k)距离 (k∈)， 那么‖f(x1)-f(y1),f(x2)-f(y2),f(x3)-f(y3),…,f(xn)-f(yn)‖≤

max{‖f(x1)-f(ν1),f(x2)-f(ν2),…,f(xm-1)-f(νm-1),f(xm)-f(νm),f(xm+1)-f(ym+1),…,f(xn)-f(yn)‖,‖f(x1)-f(ν1),f(x2)-f(ν2),…,

由k是任意正整数，有

‖f(x1)-f(y1),f(x2)-f(y2),…,f(xn)-f(yn)‖=0,这蕴含f保持0-距离。

用引理1和定理2显然可得：

根据推论1，f是仿射n-等距。

推论2 如果X与Y为实n-赋范空间满足dimX≥n，Y是n-严格凸的。如果f:X→Y，保持ρ和2ρ(ρ>0)， 那么f是仿射n-等距。

定理3 设X与Y为两个实线性n-赋范空间，Y是n-严格凸的. 如果映射f:X→Y满足

(1)‖y1-x1,...,yn-xn‖=ρ蕴含‖f(y1)-f(x1),...,f(yn)-f(xn)‖≤ρ;

(2) ‖y1-x1,...,yn-xn‖=2ρ蕴含‖f(y1)-f(x1),...,f(yn)-f(xn)‖≥2ρ,对任何x1,...,xn,y1,...,yn∈X和ρ>0 以及某个整数N成立。那么f是一个仿射n-等距。

证明(a)首先我们证明f保持w-ρ-距离，令:‖y1-x0…,yn-x0‖=ρ，以及pi=x0+i(y1-x0),i=0,1,2，那么p1=y1,p0=x0,pi-x0=i(y1-x0),pi-pi-1=y1-x0=p1-x0, 和‖pi-pi-1,y2-x0,...,yn-x0‖=‖y1-x0,...,yn-x0‖=ρ。

由条件 (1)，得到‖f(pi)-f(pi-1),f(y2)-f(x0),...,f(yn)-f(x0)‖≤ρ。

(c) 第三证明f保持w-n-2ρ-距离。根据 (a) 与(b)假定N≥3。令:

根据 (a) 和 (b)有 ‖f(pi)-f(pi-1),f(y2)-f(x),...,f(yn)-f(x)‖≤ρ,

Nρ=‖f(pN)-f(x),f(y2)-f(x),...,f(yn)-f(x)‖≤

‖f(p2)-f(p0),f(y2)-f(x),...,f(yn)-f(x)‖=‖f(p2)-f(p1),f(y2)-f(x),...,f(yn)-f(x)‖+‖f(p1)-f(p0),f(y2)-f(x),...,f(yn)-f(x)‖=2ρ。这样，

‖f(y)-f(x),f(y2)-f(x),...,f(yn)-f(x)‖=2ρ。

(d)最后根据Y是n-严格凸的，那么存在t满足f(p2)-f(p1)=t(f(p1)-f(p0))。

根据引理2，得知f是一个仿射n-等距。