改进双幂次指数趋近律的滑模控制设计

张紫方，史涛

（1.华北理工大学电气工程学院，河北唐山 063210；2.天津理工大学电气工程与自动化学院，天津 300382）

0 前言

滑模变结构控制（Sliding Mode Control，SMC）近来被广泛应用于非线性系统。SMC 控制策略主旨在于系统“结构” 虽不固定，但依然可按照滑动模态设定的轨迹使得系统到达平衡点［1-2］，且不受参数和外界干扰，这也是保证SMC 具有完全鲁棒性的根本依据。SMC 因其简单易操作、响应速度快、鲁棒性强从而被广泛应用到机器人编队、航天器飞行器等复杂的非线性系统中去。

传统的滑模控制由于控制开关不可避免的空间滞后环节，趋近平衡点时间过长使控制器延迟引发强烈抖振问题［3-4］，严重影响系统稳定性。以上问题如不解决会引起未建模系统部分消耗能量从而引起系统失稳并震荡。为解决上述抖振带来的消极影响，国内外专家创造提出趋近律的概念。现今控制器的设计基础旨在于趋近律设计。中国科学院院士高为炳［5］率先提出趋近律概念并解释分类，包含一般、等速、指数和幂次趋近律［6］，介绍趋近律旨在改变控制器内部参数从而降低抖振频率，并简单归纳了以上趋近律使用及类别，但有很大的局限性。众多学者开始致力于改变趋近律阶次，并分析各种趋近律的优势对其进行结合进而彻底消除抖振现象所带来的影响。

综上，各界学者为解决如上问题展开深入研究。LIU 等［7］在传统指数趋近律基础上创新引入幂次项设计并提出了新型指数趋近律，对比原指数趋近律成功提升了系统收敛至原点的速度。PAN 等［8］将部分滑模积分算法思想引入双幂次趋近律设计中，创新了原双幂次趋近律，加快了控制器的响应速度；但缺陷在于该算法以等速趋近律为基础，使控制器在响应速度快的同时产生频率较快的低频抖振。YU 等［9］创新引入了比例项的设计在单幂次指数趋近律中，不足点在于未充分考虑系统在扰动情况下的稳定性。廖瑛等人［10］提出一种fal 函数的双幂次函数组合趋近律，在区间［0，δ］内提升了收敛速度，并且因为构造函数为连续函数从而消除了抖振产生的影响；但构造函数缺点在于前后两端差异性过大从而影响趋近律，不具备自适应能力。张瑶等人［11］在廖瑛的研究基础上为了提高趋近律自适应能力，在组合函数中引入变幂次项，虽解决问题但系统仍然存在抖振。张国山、李现磊［12］基于改进函数构造提出一种新型的幂次趋近律，创新点在于引入tan 函数并实时调节参数跟踪系统动态特性。FALLAHA 等［13］提出一种非线性指数趋近律应用于控制器中，旨在调节系统动态特性和稳态性能，结果显示控制器良好地跟踪系统的动态性能指标，同时提升了系统的稳态特性。林洁琼等［14］为解决抖振频率大问题设计双幂次指数趋近律，结果显示系统仍存在低频抖振现象，从高频转至低频直至低频平稳，且实验对比对象单一，只参考对比了单幂次指数趋近律。杨新岩等［15］采用分段函数设计了趋近律，提出一种分段滑模幂次趋近律，在不同分段状态上设计不同参数，实验结果显示收敛速度很快并且在滑模平面上没有抖振现象产生；但不足之处在于需要调节的参数过多，而且要求控制器的精度和计算能力很高，但实际状况中很难达到要求。

基于上述研究，针对文献［14］中趋近律仍存在抖振问题，且系统快速性仿真收敛对比对象单一，对其进行改进。改进后双幂次指数趋近律，其变指数项通过改变参数和最大最小值区间，可以对系统的收敛速度、趋近时间、抖振现象调节分两阶段进行。即以为临界值，当时，系统沿滑模面平滑进入，抖振影响可忽略不计；当时，系统的动态响应显著提高，收敛速度缩短，综合提升了系统全局的收敛速度。最后考虑系统受干扰情况下稳态误差限，控制输出仍保持良好的稳态特性。通过MATLAB 仿真对比多种趋近律，验证改进后的双幂次指数趋近律在有限时间内收敛速度更快且品质更好，并且在受到系统外界扰动下仍可保持良好特性。

1 改进双幂次指数趋近律设计

1.1 相关工作基础

现阶段滑模趋近律概念作为消除或抑制抖振现象的方法之一并广泛应用，其中基础双幂次趋近律为

指数趋近律为

式中：＝-ks是指数趋近律，其解为s＝s（0）e-kt。

文献［14］中提出的双幂次指数趋近律为

其中：0＜α＜1，β＞1，k＞0。

1.2 改进双幂次指数趋近律

结合（1）（2）（3），提出一种改进的双幂次指数趋近律：

2 改进的双幂次指数趋近律特性分析

2.1 滑动模态可达性分析及证明

定理1：对于改进双幂次指数趋近律（4）（5），系统状态s可以快速运动趋近至平衡点s＝0。证明：由公式（4）可知

当且仅当s＝0 时，有＝0。

根据系统连续性，滑模趋近律存在定理及可达性定义可知，若满足≤0，则设计的趋近律满足滑动模态可达性条件，所证即所求，得文中所设计的双幂次指数趋近律式（4）可收敛至平衡点s＝0。

2.2 系统收敛时间分析及证明

定理2：对于改进双幂次指数趋近律式（4），假设s的初始状态为s0，则与之对应的状态s和均可在有限时间内到达滑模面且收敛至0，收敛时间小于（t1＋t2＋t3）。其中t1、t2、t3表达式如下：

证明：假设1＜λ＜s0，将全局过程分成3 个阶段进行。

第一阶段：系统从s0到st1，此时趋近律式（4）可写成：

求解上述方程，因未知项参数过多，可将方程分两步求解。首先对1sλ＝k3s这部分进行求解，其过程如下：

假设存在中间变量y＝s1-λ，公式（11）可写成：

求解一阶微分线性方程，令y＝u（t）exp（-∫（1-λ）k3dt），u＝u（t）表示t是连 续函数，代入公 式（12）得：

对式（13）两边进行积分：

C为常数，求解过程如下：

化简可得：

令时间t＝0，可解得常数C

联立公式（16）（17）即可求得系统从s0运动到st1所需时间t1为

同理可得第二阶段，系统由s（t1）运动至s（t2）的时间t2和第三阶段，系统由s（t2）运动至s（t3）的时间t3。

所以系统由s（t1）＝1 运动至s（t2）＝β所需时间小于t2，系统由s（t2）＝β运动至s（t3）＝0 所需时间小于t3。此时可得出结论系统所需收敛总时间小于（t1＋t2＋t3）。

2.3 系统稳态误差分析

考虑到提出的改进双幂次指数趋近律会受到不确定性扰动影响，系统变为

系统期望误差小于δ，δ为非常小的正数。

定理3：对于任意的ki ＞0（i＝1，2，3），β＞1，存在正数k1＞0，0＜α＜1，且0＜D＜k1＜D／δ1，0＜δ≤logδ1（D／k1）（0＜δ1≤δ）时，系统式（21）可在有限时间内收敛于δ。

证明：选择Lyapunov 函数：

求导得：

表达式（23）可替换为

定理4：假设系统状态（x），f∈Rn，且x∈D⊂Rn，D为平衡点附近的区域，设此时存在连续函数V并满足正定，且除平衡点外均负定；同时存在一个领域M⊂D和一个实数μ＞0，0 ＜η＜1，使得＋μVη≤0，那么（x）就能在有限时间收敛到平衡点。

根据定理4 可知，系统状态可以收敛至，代入公式（23），计算得：

通过计算，定理4 得证。

3 实验仿真及分析

3.1 仿真模型和控制器设计

首先建立控制器结构和仿真模型，控制器结构拟采用双闭环结构控制，该控制器控制下的机器人流程如图1 所示。

图1 双闭环控制的轮式机器人控制流程Fig.1 Control flow of wheeled robot with double closed loop control

仿真模型采用轮式机器人，轮式机器人运动模型为

式中：θ表示机器人运动的偏转角；x、y表示机器人实际位姿；v、ω分别表示机器人实际线速度和角速度。

理想情况下系统轨迹跟踪误差如下：

式中：［xe，ye，θe］T表示轮式机器人实际偏差量；［xq，yq，θq］T表示机器人期望偏差量。

对式（28）求导结合趋近律式（4）（5）

其中：ωq、vq分别表示轮式机器人期望角速度、线速度。由此设计合适的滑模面，为了使机器人轨迹跟踪误差xe、ye、θe均可在有限时间内收敛至零点，设计的滑模面为

其中：ωq≠0 且为常数。

上式满足改进的双幂次指数趋近律：

公式（29）—（31）联立获得控制器表达式为

3.2 改进前后双幂次指数趋近律对比

通过MATLAB 进行仿真实验，对文献［14］提出的双幂次指数趋近律在控制器中抖振现象进行复现，如图2 所示。

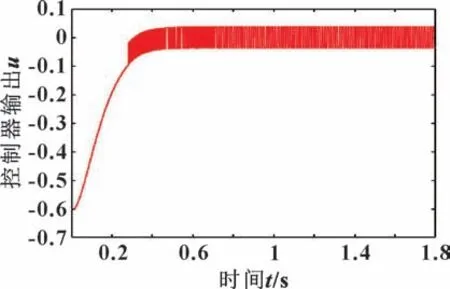
图2 文献［14］基于双幂次指数趋近律控制器输出曲线Fig.2 Output curve based on a double power exponential convergence law controller in literature［14］

由图2 可知：文献［14］采用的双幂次指数趋近律，在控制器作用下系统运动到滑模面时，产生了强烈的高频抖振，之后由于趋近律的作用减缓抖振，使得系统保持均匀的低频抖振运动，即减缓了抖振但没有消除抖振对系统带来的影响。

由图3 可知：本文作者提出改进后的双幂次指数趋近律，在控制器作用下系统运动至滑模面时间延长了0.2 s 左右，随后出现了极轻微的低频抖振，影响可忽略不计，最后在改进后趋近律作用下明显消除了抖振。由此验证了改进后的双幂次指数趋近律最大限度地消除了系统抖振，在理想时间内跟踪控制器输出轨迹，良好地提升了系统的动态特性。

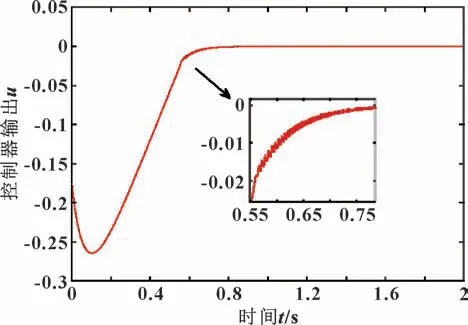
图3 改进后基于双幂次指数趋近律在控制器中的输出曲线Fig.3 Output curve in controller based on improved double power exponential reaching law

3.3 系统快速收敛性仿真对比

考虑单输入单输出非线性系统：

式中：d（t）为扰动变量且有界；s为系统滑模变量；u为系统控制输入。

对于已确定的系统式（34），分别采用如下趋近律作为系统快速收敛性仿真对比：文献［8］中的双幂次等速趋近律，快速幂次趋近律，文献［14］中的双幂次指数趋近律，文献［10］中的fal 函数组合趋近律，文献［15］中的分段滑模幂次趋近律，和改进的双幂次指数趋近律。

其中文献［10，15］趋近律分别为

为了保证趋近律对比仿真的有效性，参数设置和相同项系数设定大致相等。

设置参数k1＝1，k2＝1，k3＝1，k4＝1，α＝2，β＝0.5，λ＝0.5，N＝5，p＝2。系统初始状态设置s0＝10.0，sm＝10.05。对上述趋近律进行仿真对比，仿真结果如图4、5 所示。

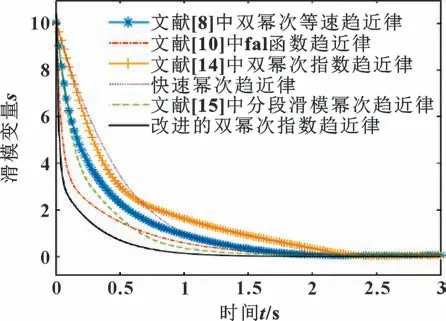
图4 滑模趋近律随时间收敛曲线对比Fig.4 Comparison of convergence curves of sliding mode convergence law over time

通过实验，若设置的初始值s0较小，则趋近律收敛效果彼此接近不足以区分效果，故设置初始值s0＝10，区分效果明显。由图4 可知：文中改进的双幂次指数趋近律具有最佳收敛速度，滑模状态s在最快时间内趋近于零点，同时系统没有产生抖振现象。且由图5 可知：在0.25 s 前文献［15］提出的分段滑模趋近律趋于零点速度最快，但因其涉及分段函数，需要考虑参数过多，因此在0.25 s 后文中改进的双幂次滑模趋近律更快收敛到零点处。由此验证了文中所改进的趋近律具有最佳实用性及有效性。

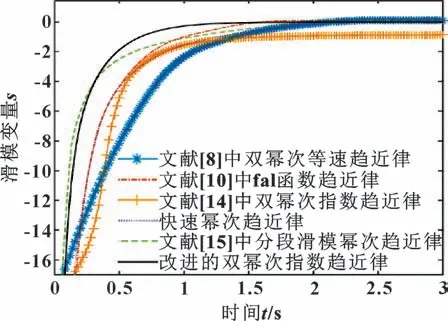
图5 控制量随时间收敛曲线对比Fig.5 Comparison of convergence curves of control variables over time

3.4 干扰下稳态误差界仿真

将滑模模态初始值设置为12，对于不确定系统式（34），外界所受一切扰动用d（t）表示，对外界干扰下的稳态误差界进行仿真。

设置干扰上界数值为12，代入系统中，且d＝sin2t＋cos2t，控制输出u仿真结果如图6 所示。

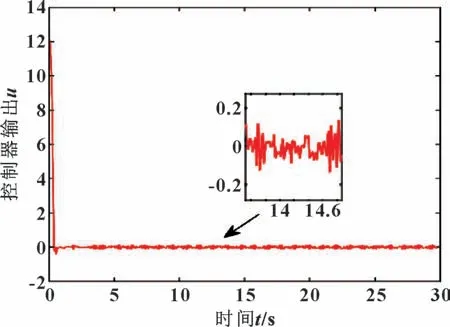
图6 干扰下滑模输出u 收敛曲线Fig.6 Convergence curve of sliding mode output u under interference

由图6 可知：受到干扰下，系统收敛时间约为0.7 s，稳态误差界在±0.2 s 内，可验证文中所提双幂次指数趋近律在外界干扰下具有极好的稳态特性。当系统存在外界扰动或不确定因素下，滑模变量仍可在最快时间收敛至平衡点附近，趋近律依然可以获得良好效果。

4 结语

提出一种改进的双幂次指数趋近律，通过灵活设计参数改进变指数项设计，并运用新的函数组合，提出了新的双幂次指数趋近律，之后对文中趋近律进行分析。首先在理论上验证改进后的趋近律能够快速收敛到平衡点且削弱抖振影响，再通过实验对比，对其他文献中各种趋近律进行比对分析，验证了所提出的趋近律不仅消除了抖振影响，且具有最佳性能和实用性。最后再通过实验验证在系统存在干扰下，文中趋近律仍然可以快速收敛至平衡点附近，说明改进后的双幂次指数趋近律具有显著的优越性。