基于干扰观测器的机电伺服系统PI 控制策略

吕晨，欧阳权，许文波，王志胜

（1.南京航空航天大学自动化学院，江苏南京 210016；2.北京精密机电控制设备研究所航天伺服驱动与传动技术实验室，北京 100076）

0 前言

空气舵伺服系统是飞行器制导与控制系统的执行机构，通过带动舵面摆动实现飞行器姿态控制。随着数字处理器技术、永磁材料和电力电子器件的发展，采用永磁同步电机的机电伺服系统凭借其轻质高效、高可靠、易维护、易安装等优点近年来在航空航天飞行器中得到了广泛使用［1-2］。然而，机电伺服系统是一个非线性、多变量、强耦合系统，传统的PID 控制存在鲁棒性较差、控制器参数较为固定、参数整定困难、对系统参数变化和外界干扰敏感等缺点［3］，难以应用于某些对动静态性能要求较高的场合。加上飞机运行环境中存在多种未知的动态扰动，会造成引起性能波动，因此影响了伺服系统的性能，并且容易引起谐振，甚至导致系统的不稳定，从而严重影响飞行器的安全性。

目前，为了抑制干扰对机电伺服系统的影响，各个领域的专家学者提出了不同的抗干扰控制方法，如内模控制、输出调节理论、随机控制理论等。从抗干扰能力上区分，这些抗干扰控制方法可以分为以下两类：干扰抑制方法和干扰抵消或补偿方法。干扰抑制方法是利用干扰的性能指标对干扰进行抑制，如H∞控制、随机控制理论［4］、滑模控制［5］等。干扰抵消或补偿方法是基于一些特征信息对干扰进行重构，得到干扰估计值，然后利用这个估计值抵消干扰对系统的影响，如自抗扰控制［6-7］、内模控制［8-9］、输出调节理论、基于干扰观测器的控制理论［10-12］等。

与其他抗干扰控制方法相比，基于干扰观测器的控制方法（Disturbance -Observer -Based -Control，DOBC）具有结构简单、容易实现等优点。近年来，DOBC 在机器人系统［13］、硬盘驱动系统、伺服系统、航空航天等系统中得到广泛应用。为此，本文作者提出了一种基于神经网络干扰观测器的空气舵机伺服系统控制策略，运用神经网络观测器进行非线性干扰的在线估计，再进行PI 控制保证系统获得期望的舵面跟踪精度。文中的主要创新点如下：

（1）设计了基于神经网络观测器，能对空气舵机电伺服系统的状态和未知干扰进行精确估计。

（2）传统伺服系统以电机转角进行反馈控制，在舵面伺服系统中抗干扰效果较差；以观测器中舵面角度估计值进行反馈控制抗干扰效果有明显提升。

1 空气舵机电伺服系统模型分析

空气舵机电伺服系统的主要任务是接收摆角指令，然后驱动舵面按照指定角度进行摆动。本文作者以空气舵机电伺服系统为研究对象，它主要由机电作动器和摇臂组成，机电作动器是由永磁同步电机（Permanent Magnetic Synchronous Machine，PMSM）、齿轮箱和滚珠丝杠组成。结构模型图1 所示，其中忽略了电机和舵轴的黏性阻尼。

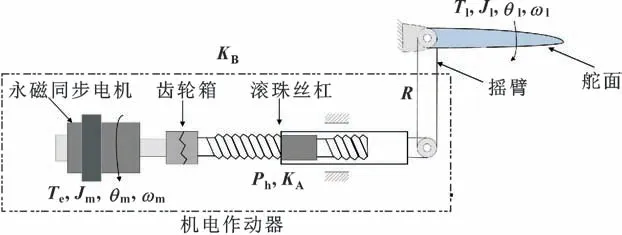
图1 空气舵机电伺服系统动力学模型Fig.1 Dynamics model of air rudder electromechanical servo system

图1 中：Jm、θm、ωm分别为电机转动惯量（含减速器、滚珠丝杠）、电机角位移和电机机械角速度；Jl、θl、ωl分别为负载转动惯量、负载角度、负载角速度；Te为同步旋转坐标系下，id＝0 时电机的电磁转矩；KA、KB分别为机电作动器刚度和机电作动器安装支承刚度；Ph为滚珠丝杠导程（含减速器）；R为空气舵摇臂长度；Tl为负载转矩（含铰链力矩、舵轴摩擦力矩、阻尼力矩及模型参数的不确定性产生的力矩等）。空气舵机电伺服系统的数学模型为

进一步简化表示，定义状态向量x＝[x1，x2，x3，x4]T≜[θm，ωm，θl，ωl]T∈R4，输 入u≜iq∈R，测量输出m≜θm∈R，命令输出y≜θl∈R。基于式（1）可以将空气舵机电伺服系统的动力学模型写为以下状态空间表达式：

w＝-RTl／（JlPh），在模型中被视为未知转矩扰动项。

从公式（2）可以看出，如欲使舵面的旋转角位移y跟踪其期望值yd＝，而在实际的伺服系统中，测量传感器通常设置在电机侧或滚珠丝杠处，这意味着可以直接测量电动机的角位移θm而不是θl，因此y不能直接测量，必须使用m而不是y作为反馈量来实现对y的高性能控制。且未知转矩扰动的存在给基于模型的机电伺服控制策略的设计带来了困难。如何抑制伺服系统因扰动而产生的指令跟踪误差，是亟待解决的难题。

2 基于干扰观测器的伺服控制算法

为了弥补上述难题，本文作者设计了一种基于干扰观测器的机电伺服系统控制策略，如图2 所示。首先，设计了全维神经网络观测器用于系统状态估计，RBF 神经网络用于模型不确定性w的在线估计。然后针对机电伺服系统，将x3的估计值替换传统位置环中的x1，使得y成为其期望的yd。

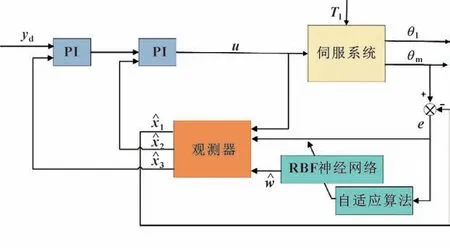
图2 控制器示意Fig.2 Controller schematic

2.1 基于RBF 神经网络的观测器

为了估计舵面y＝x3的旋转角位移，基于模型（2），设计了一种基于神经网络的观测器，使用RBF神经网络近似模型不确定扰动：

其中：∈R4是x的估计；L是设计的观测器增益向量；而是w的估计，它是一个RBF 神经网络，可以计算为

其中：W＝[w1，w2，…，wn]T∈Rn是权重向量；n表示神经网络节点的数量；S（）＝［s1（），…，sn（）］T∈Rn表示激活函数向量，si（）（1≤i≤n）满足：

其中：η1和η2是设计的正常数。参考文献［14］，具有足够数量的神经节点的RBF 神经网络可以近似任何连续函数。根据RBF 神经网络的逼近性质，不确定项w可以替换为

其中：W*是理想的常权重向量；ξ是近似误差。由于在实践中w是有界的，因此可以推导出理想常数权重W*是有界的，可以表示为如下：

其中：WM是一个正常数。

2.2 稳定性分析

设＝x-，＝W*-W，由式（2）（6）（7）可以推导出：

式（9）中：ε是有界的，满足和εM≥0。从式（2）中可以看出（C，A）是可观测的，因为

是满秩的。因此可以找到正定对称矩阵P满足：

其中：Q也是正定矩阵。选择Lyapunov 函数为

V的导数可以计算为

通过完全平方可以得到：

根据式（10）（13），可以推导出以下不等式：

其中：λm（Q）表示Q的最小特征值。通过定义

由于有界，则a为正有界，b有界。因为-a是负的，显然式（17）是稳定的。因此的有界性也可以得到保证［16］。

3 仿真验证

基于MATLAB／Simulink 仿真平台，对所提出的基于干扰补偿的空气伺服系统控制策略进行了验证，并与常规位置环电机转角反馈控制策略进行了比较。由于实际伺服系统存在库仑摩擦和黏滞摩擦，将摩擦也考虑加入仿真。空气舵伺服系统的参数和控制参数如表1 所示。

表1 空气舵机电伺服系统的参数Tab.1 Parameters of air rudder electromechanical servo system

3.1 常值扰动系统时域仿真分析

在系统初始就存在常值扰动。以Tl＝100 N·m 情况为例，对系统输入0.5 rad 摆角信号指令，其舵面摆角估计效果如图3 所示，系统响应曲线如图4 所示。类似上述仿真步骤，当Tl＝300、500 N·m 时，仿真结果如图5—6 所示。常值扰动效果对比如表2所示。

表2 常值扰动效果对比Tab.2 Comparison of constant disturbance effects

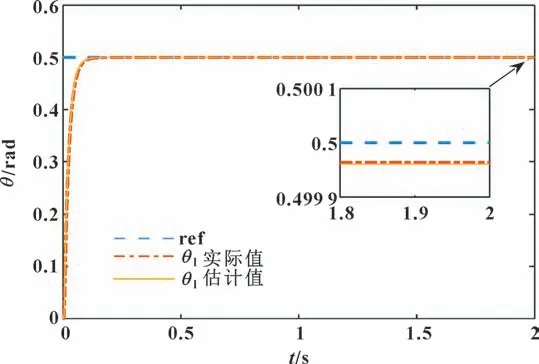
图3 常值扰动Tl＝100 N·m 下的θl估计效果Fig.3 Estimated effect of θl at constant disturbance Tl＝100 N·m

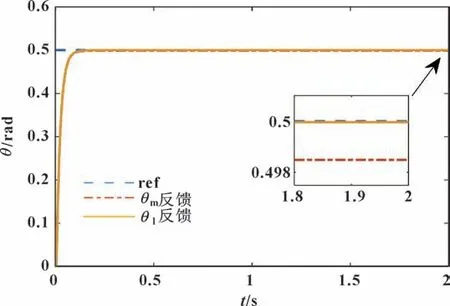
图4 常值扰动Tl＝100 N·m 下的系统响应Fig.4 System response at constant disturbance Tl＝100 N·m

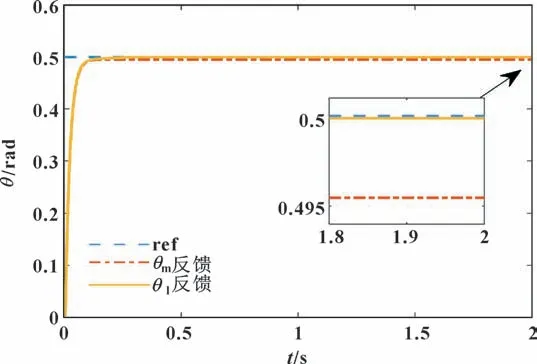
图5 常值扰动Tl＝300 N·m 下的系统响应Fig.5 System response at constant disturbance Tl＝300 N·m

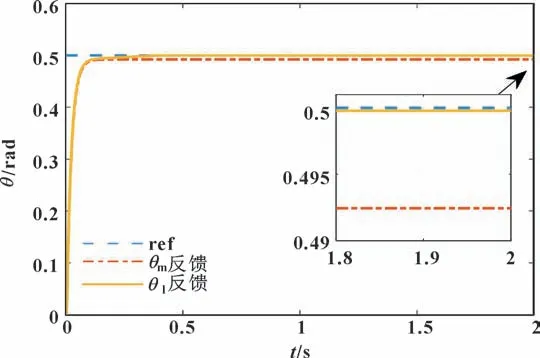
图6 常值扰动Tl＝500 N·m 下的系统响应Fig.6 System response at constant disturbance Tl＝500 N·m

从仿真结果来看，当系统初始就存在不同常值干扰力矩，文中设计的干扰观测器反馈控制相比传统θm反馈控制，稳态误差减少97%以上，动态过程更平滑，稳态精度较高。

3.2 扰动抑制时域仿真分析

对系统输入0.5 rad 摆角信号指令，在1 s 时对系统施加干扰力矩Tl。以Tl＝100 N·m 情况为例，对系统输入0.5 rad 摆角信号指令，其舵面摆角估计效果如图7 所示，系统响应曲线如图8 所示。类似上述仿真步骤，当Tl＝300、500 N·m 时，仿真结果如图9—10 所示。阶跃扰动效果对比如表3 所示。

表3 阶跃扰动效果对比Tab.3 Comparison of step disturbance effects

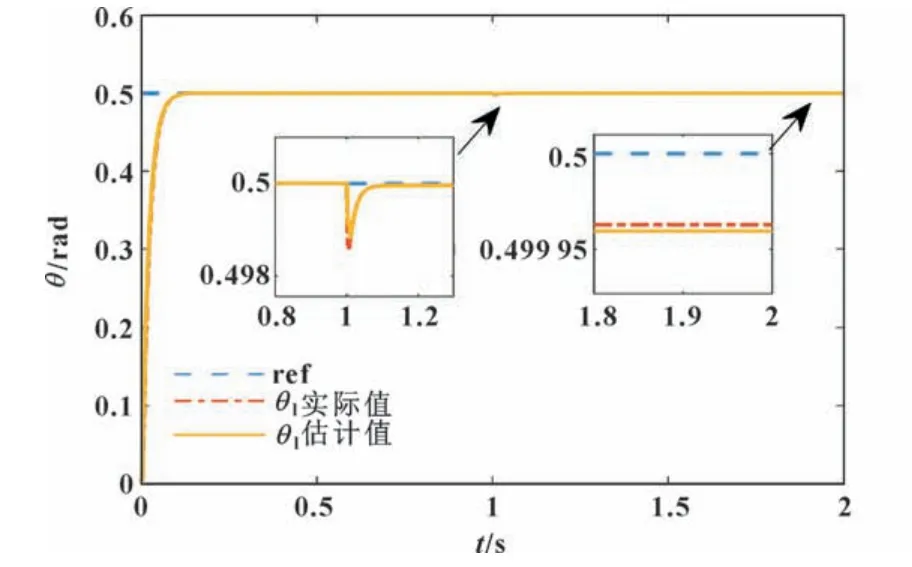
图7 阶跃扰动Tl＝100 N·m 下的θl估计效果Fig.7 Estimated effect of θl at step disturbance Tl＝100 N·m

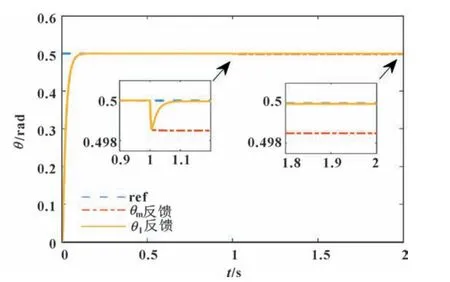
图8 阶跃扰动Tl＝100 N·m 下的系统响应Fig.8 System response at step disturbance Tl＝100 N·m

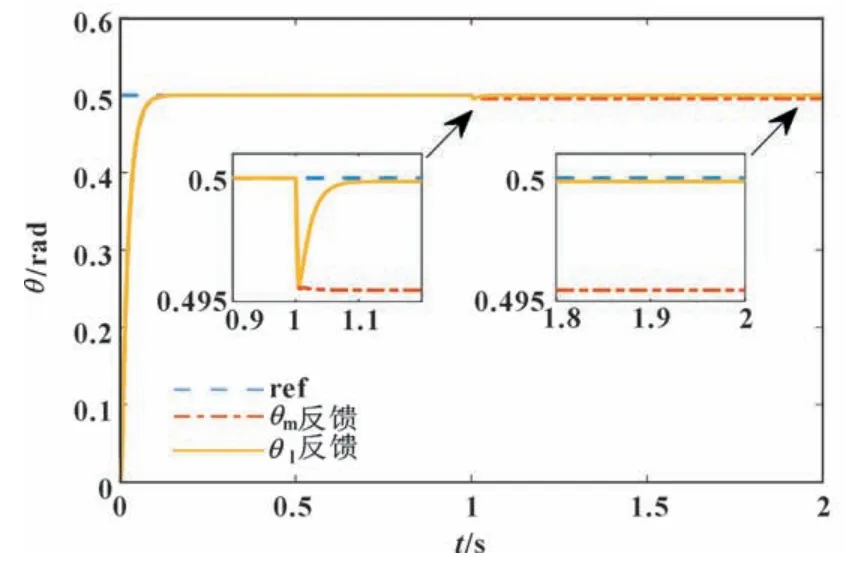
图9 阶跃扰动Tl＝300 N·m 下的系统响应Fig.9 System response at step disturbance Tl＝300 N·m

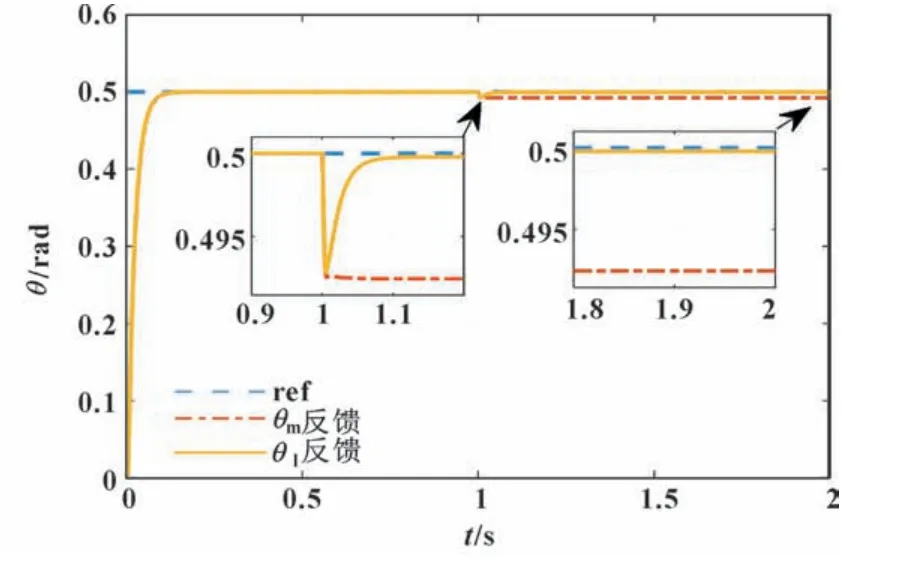
图10 阶跃扰动Tl＝500 N·m 下的系统响应Fig.10 System response at step disturbance Tl＝500 N·m

从仿真结果来看，当系统存在不同阶跃干扰力矩，设计的干扰观测器反馈控制相比传统θm反馈控制，稳态误差减少97%以上，稳态精度较高，抗扰动效果更好。

4 结论

设计一种基于RBF 神经网络的状态观测器，对空气舵机电伺服系统外部扰动进行观测补偿。仿真结果表明：相比传统方法，该方法可以在较短时间内完成外部干扰的高精度补偿，控制精度更高。