基于集中式卡尔曼滤波干扰观测器的无模型自适应控制

徐通福，李秀英

（上海应用技术大学电气与电子工程学院，上海 201418）

0 前言

随着计算机在工业控制领域的广泛应用，数据驱动控制方法特别是离散时间非仿射非线性系统的数据驱动自适应控制具有重要意义。该方法仅利用被控装置的实测闭环输入输出数据进行设计，可以避免传统基于模型的自适应控制系统中无法解决的精确建模和模型约简、未建模的动力学、鲁棒性、持续激励条件和闭环控制等问题［1］。由于输入输出测量数据包含了所有的被控对象动力学信息，从而导致传统基于模型意义上的系统建模、未建模动力学、模型约简和鲁棒性等概念消失。

无模型自适应控制（Model Free Adaptive Control，MFAC）作为一种典型的数据驱动控制方法，利用伪偏导数（Pseudo Partial Derivative，PPD）或伪梯度（Pseudo Gradient，PG）矢量的新概念在每个工作点通过所谓的动态线性化数据模型设计控制器，控制器参数的整定方法基于使用闭环测量数据的确定性估计算法［2］。MFAC 由于具有计算简单、无需建模等优点，已被应用于车辆、储能电池、磁悬浮和数控机床等许多领域［3-6］。到目前为止，MFAC 的鲁棒性仍然是一个悬而未决的问题。在基于模型的控制理论中，鲁棒性是指处理未知的不确定性或未建模动态的能力。然而，无模型控制方案只利用被控装置的输入输出数据进行控制器设计，不涉及系统的任何模型信息，因此不存在未建模的动力学。从这个角度来看，传统的控制系统的鲁棒性已经不存在了。对于任何实际控制问题，输入输出数据都可能受到外部干扰，或由于传感器、执行器或网络故障而导致数据丢失。因此，研究未知干扰或数据丢失对无模型自适应控制算法性能的影响很有必要［7］。在工业环境中，测量从来不是完美的。它们可能会被各种噪声所扭曲。因此，对有测量干扰的MFAC 算法进行研究，无论在理论方面还是在实际应用中都具有重要意义。

近年来，许多学者对具有测量干扰的MFAC 算法进行了研究。一种改进的带滤波器的MFAC 算法有效抑制了测量扰动的影响［8］，该方法通过设计低通去除高频噪声信号，但实际中噪声信号频率多样。针对测量扰动信号，提出了一种跟踪微分器对扰动进行抑制，但该方法会使系统相位发生改变［9-10］。一种小波阈值去噪的方法被提出，该方法能够对噪声进行实时自适应过滤，但存在阈值难以设定的问题［11］。针对电液伺服系统存在不确定性干扰和不确定性因素的情况，径向基神经网络干扰观测器被提出去估计扰动，并将其补偿到控制器的设计中，从而有效减小了扰动对系统的影响，但这种方法增加了系统的复杂性［12］。一种改进的卡尔曼滤波MFAC 算法被用来抑制测量扰动，该方法假设系统噪声和测量噪声相互独立，但是大多数情况下系统噪声和测量噪声之间是相关的，而且该方法只考虑了单个传感器的测量结果［13］。基于此，本文作者提出一种基于集中式卡尔曼滤波干扰观测器的MFAC 方法，该方法将多个传感器的测量结果进行最优集中式卡尔曼滤波融合，并且考虑系统噪声和测量噪声以及各个传感器之间的测量噪声都是相关的情况。相比只使用单个传感器的卡尔曼滤波MFAC 算法来说，基于多传感器的集中式卡尔曼滤波干扰观测器MFAC 算法具有更好的跟踪性能和更大的信噪比。

1 问题描述

考虑一类SISO 离散时间非线性系统：

其中：u（k）和y（k）分别表示k时刻系统的输入和输出；ny、nu是两个未知的正整数；f（…）代表未知的非线性函数。

假设1：除有限时刻点外，f（…）对u（k）的偏导数连续。

假设2：除有限时刻点外，系统公式（1）满足广义的利普席兹条件。

定理1：对满足假设1 和假设2 的非线性系统公式（1），当时，一定存在一个被称为PPD 的时变参数φc（k），使得系统公式（1）转化为如下线性模型［14］：

若系统存在测量扰动，则系统的输出测量值为

其中：d（k）代表测量扰动，且，d是正常数。

系统存在测量扰动时，MFAC 控制方案为

其中：λ＞0，μ＞0，ρ∈（0，1］，η∈（0，1］；ε是一个充分小的正数；（1）是（k）的初值；y*（k＋1）代表系统的期望输出。

由式（6）可知，控制器的设计依赖于系统期望输出与测量输出的误差值。当系统不存在测量扰动时，在MFAC 控制方法的作用下，系统的输出误差可以收敛至0［14］。而当系统受到测量扰动的影响时，在MFAC 控制方法的作用下，系统的输出误差收敛到一个大于0 的常数［8］。可见，当系统存在测量扰动时，MFAC 控制方法的控制性能会显著降低。

2 基于集中式卡尔曼滤波干扰观测器的MFAC方法

2.1 集中式卡尔曼滤波干扰观测器的设计

考虑如下方程所描述的非线性离散系统：

其中：状态y（k）代表系统在时刻k时的系统输出；ω（k-1）表示系统噪声，假设其为零均值的高斯白噪声，方差为，且系统噪声误差协方差矩阵为Q（k-1）；ymi（k）代表传感器i在时刻k时的测量输出；Ci（k）代表系统的观测阵；vi（k）表示传感器i的测量噪声，与系统噪声ω（k-1）相关，其相关的强度与βi的取值有关；N代表传感器的个数；γi（k）是零均值高斯白噪声，方差为，并且与系统噪声ω（k-1）相互独立。当i≠j时，对k，l＝1，2，…，有：

其中：δkl表示克罗尼克δ函数。从上面的描述可以看出，在同一时刻不同传感器的测量噪声是相关的，并且每个时刻的测量噪声都和上一时刻的系统噪声相关。式（7）将非线性系统等价转换为线性系统，并且上述对于实际环境噪声的假设是合理的，这与相关噪声环境下多传感器数据融合的假设一致。

集中式卡尔曼滤波干扰观测器是通过将所有的观测方程集中为一个观测方程，然后在每一时刻利用该时刻的集中观测方程与上一时刻最优输出的估计值得到当前时刻的输出预测值，并且利用传感器当前时刻的输出测量值对卡尔曼增益进行校正。集中式卡尔曼滤波干扰观测器的结构如图1 所示。

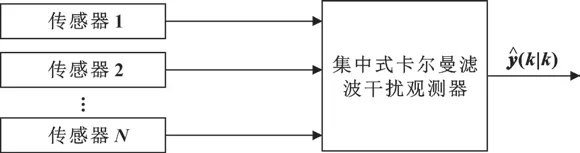
图1 集中式卡尔曼滤波干扰观测器的结构Fig.1 Structure of centralized Kalman filter disturbanceobserver

假设k-1 时刻y（k-1）的一个最优状态估计为，则k时刻y（k）的最优集中式估计算法［15］为

其中：当噪声不相关时，R（k）是对角矩阵，即非对角线部分的值全为0 且S（k）＝0，此时，所提出的最优集中式估计算法退化为噪声无关情况下的算法。因此，文中讨论的噪声相关下的最优集中式估计算法更具一般性。

从上式中可以看出，集中式卡尔曼滤波增益与Q（k-1）和R（k）的值息息相关，而当前时刻集中式卡尔曼滤波干扰观测器的估计值等于上一时刻卡尔曼滤波干扰观测器的估计值和传感器测量值ym（k）的加权和，因此与Q（k-1）和R（k）的值也息息相关。

2.2 基于集中式卡尔曼滤波干扰观测器的MFAC算法

将传感器的测量值和数据模型的预测值经过集中式卡尔曼滤波干扰观测器滤波输出，然后将该输出与系统的期望输出值的偏差信号送入MFAC 控制器的设计中，从而得到基于集中式卡尔曼滤波干扰观测器的MFAC 控制方案。算法结构如图2 所示。

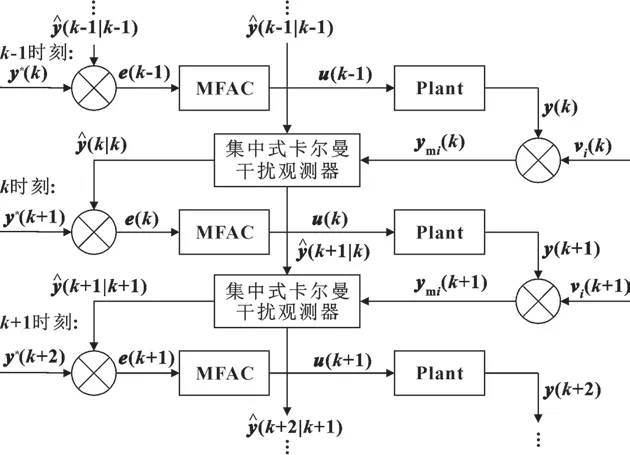
图2 基于集中式卡尔曼滤波干扰观测器的MFAC 算法结构Fig.2 MFAC algorithm structure based on centralized Kalman filter disturbance observer

结合图 2，公式（10）—（14）和公式（19）—（21）构成了完整的基于集中式卡尔曼滤波干扰观测器的MFAC 控制方案：

其中：式（10）—（14）是集中式卡尔曼滤波干扰观测器算法，该算法的目的是为了得到滤波后的预测输出；式（19）—（21）是基于集中式卡尔曼滤波干扰观测器MFAC 算法，与常规MFAC 算法的不同之处在于，该算法利用干扰观测器的输出去设计控制器，而不是直接利用传感器的测量值去设计，这样有效规避了测量扰动对常规MFAC 算法控制性能的影响。

3 仿真

为验证基于集中式卡尔曼滤波干扰观测器的MFAC 算法的有效性，给出由3 个传感器组成的集中式卡尔曼滤波干扰观测器（集中式观测器）的MFAC算法，基于传感器1 的卡尔曼滤波干扰观测器（局部观测器1）的MFAC 算法，基于传感器2 的卡尔曼滤波干扰观测器（局部观测器2）的MFAC 算法和基于传感器3 的卡尔曼滤波干扰观测器（局部观测器3）的MFAC 算法的仿真对比试验。并且利用均方根误差（Root Mean Square Error，RMSE）和 信噪比（Signal Noise Ratio，SNR）两个指标对5 种控制算法的控制性能进行比较：

其中：δRMSE代表各个时刻的实际值与期望值误差平方和，其值越小，系统控制性能越好；δSNR代表信号与噪声的方差比，其值越大，系统的去噪能力与控制性能越好。

例1 考虑如下非线性系统［13］：

期望输出信号为

由图3—4 可知：当系统存在测量扰动时，MFAC控制算法的跟踪误差会显著增加；采用基于单个传感器卡尔曼滤波干扰观测器的MFAC 算法后，系统的控制性能优于MFAC 算法；而对于各个局部干扰观测器来说，在系统噪声方差和噪声相关系数相同的情况下，局部干扰观测器的γi（k）的噪声方差越小，基于该局部卡尔曼滤波干扰器的MFAC 算法的控制性能越好。当采用基于集中式卡尔曼滤波干扰观测器的MFAC 算法后，系统的控制性能又优于只使用单个传感器卡尔曼滤波干扰观测器的MFAC 算法。除此之外，基于集中式卡尔曼滤波干扰观测器的MFAC 算法的响应速度比MFAC 算法和基于单个传感器卡尔曼滤波干扰观测器的MFAC 算法的响应速度快。可见，集中式卡尔曼滤波干扰观测器的MFAC 算法能有效提高存在测量扰动的时不变参考信号的跟踪能力。

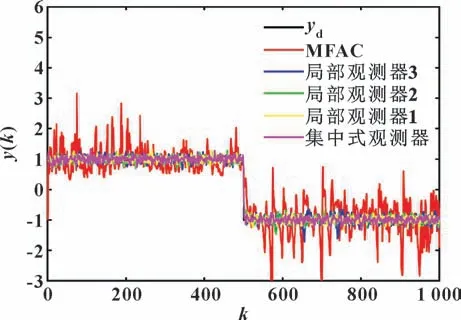
图3 时不变参考信号跟踪性能比较Fig.3 Comparison of tracking performance of time-invariant reference signal

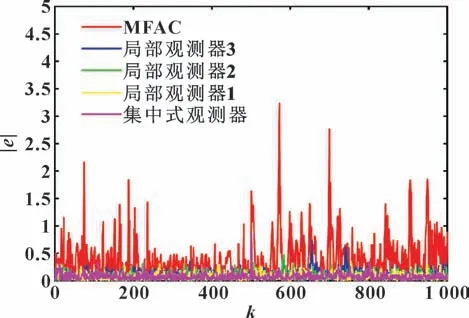
图4 时不变参考信号跟踪误差绝对值比较Fig.4 Comparison of the absolute value of tracking error of time-invariant reference signal

例2 考虑如下非线性系统［14］：

期望输出信号：

设置此例中的系统噪声和测量噪声的相关参数值、系统的初始参数值、系统的控制器参数值均和例1 中的参数值一致。5 种控制算法的跟踪性能如图5和图6 所示。

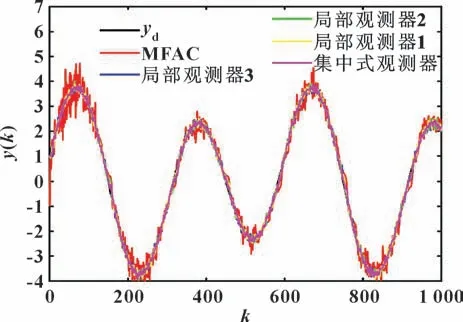
图5 时变参考信号跟踪性能比较Fig.5 Comparison of tracking performance of time-varying reference signal

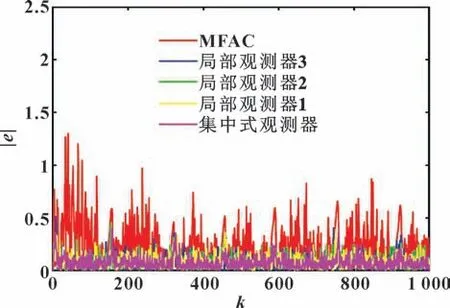
图6 时变参考信号跟踪误差绝对值比较Fig.6 Comparison of the absolute value of tracking errors of time-varying reference signal

由图5—6 可知：MFAC 算法的控制性能最差，基于集中式卡尔曼滤波干扰观测器的MFAC 算法的控制性能最好，因此，基于集中式卡尔曼滤波干扰观测器的MFAC 算法对时变的参考信号依然可以很好地抑制测量扰动对MFAC 算法的影响，大大提升系统的跟踪性能。

综合上述的两个例子，使用RMSE 和SNR 指标对5 种控制算法的控制性能进行比较，结果如表1所示。

表1 5 种控制算法的控制性能比较Tab.1 Comparison of control performance of five control algorithms

根据图3—6 和表1 的数据可知：本文作者提出的基于集中式卡尔曼滤波干扰观测器的算法相比MFAC 算法和基于局部卡尔曼滤波干扰观测器的MFAC 算法，在时不变参考信号和时变参考信号并且在噪声相关的情况下具有更好的抑制测量扰动的效果，在算法具有适用性的同时具有更小的均方根误差和更大的数据信噪比，可以显著提升在测量扰动作用下系统的控制性能。

4 结论

本文作者针对具有测量扰动的非线性系统，提出一种基于集中式卡尔曼滤波干扰观测器的MFAC 算法。将所提出的算法与MFAC 算法和基于局部卡尔曼滤波干扰观测器的MFAC 算法分别在时不变参考信号和时变参考信号下进行对比，仿真结果表明：在具有适用性的同时，集中式卡尔曼滤波干扰观测器的MFAC 算法具有更强的抗干扰能力、更小的均方根误差和更大的数据信噪比等优点，可以显著提升MFAC算法在测量扰动下的控制性能。