斜齿轮对角修形设计研究
贾海涛,邵 钢,栾圣罡
(中国船舶重工集团公司第七〇三研究所,黑龙江 哈尔滨 150078)
0 引 言
军舰在巡航时必须保持足够安静以防止被声呐系统探测到,但巡航时动力系统旋转机械所产生的噪声尤为突出。通过对主减速齿轮装置实船监测表明,在巡航工况下,齿轮的啮合频率以及2倍频等特征频率的振动幅值相对比较突出,这是影响动力系统中高频振动噪声的主要原因。大量实验和研究表明,齿轮噪声的60%~80%与轮齿齿面精度、齿轮啮合刚度特性和轮齿啮合冲击直接有关。在提高齿轮精度方面,对于最初低精度齿轮来说减振降噪效果明显,但随着齿轮加工能力的不断提高,目前舰船齿轮精度也不断得到改善,但它对降低齿轮噪声的作用越来越小。同时,由于轮齿受载后的变形会不可避免造成轮齿初始啮合点移位,引起啮合冲击而产生振动。
自从1938年,Walker[1]首先提出对直齿轮进行修形的必要性以来,齿轮修形技术是减少啮合冲击及降低振动噪声的有效方法之一。常规的方法为齿廓修形和齿向修形,为二维修形,这种修形方式沿整个齿宽具有相同的齿廓修形量和修形高度,对齿轮重合度减少较多。对于斜齿轮,由于螺旋角的存在,齿轮啮合线为一系列的斜线,啮入啮出在齿面齿根和齿顶角很小的区域,对角修形较常规修形相比较,齿面没有修整的部分小很多,保留齿面更大的有效承载面积,可使齿面接触应力降低。
本文针对船用主减速齿轮装置,提出了其对角修形的设计要点,利用ANSOL软件,通过轮齿接触分析验证了对角修形的有效性。
1 对角修形的基本原理
斜齿圆柱齿轮与直齿圆柱齿轮的啮入和啮出情况不同,直齿圆柱齿轮的瞬时接触线是沿齿宽方向的直线,其啮入啮出是在整个齿宽方向上完成的,而斜齿圆柱齿轮由于轮齿与回转轴线偏斜了一个角度,所以轮齿上的瞬时接触线是一系列斜线,斜齿轮的啮入、啮出是从齿面的齿顶角和齿根角部实现的,如图1所示。对角修形的实质是只改变斜齿轮啮入角和啮出角,其余齿面保持不变。

图 1 常规修形与对角修形示意图Fig. 1 General modification and triangular end modification sketch map
2 对角修形的基本原理
斜齿圆柱齿轮与直齿圆柱齿轮的啮入和啮出情况不同,直齿圆柱齿轮的瞬时接触线是沿齿宽方向的直线,其啮入啮出是在整个齿宽方向上完成的,而斜齿圆柱齿轮由于轮齿与回转轴线偏斜了一个角度,所以轮齿上的瞬时接触线是一系列的斜线,斜齿轮的啮入、啮出是从齿面的齿顶角和齿根角部实现的,如图2所示。对角修形的实质是只改变斜齿轮啮入角和啮出角,其余齿面保持不变。

图 2 对角修形齿轮模型Fig. 2 Triangular end modification model
3 建立对角修形模型
对角修形为三维修形,轮齿修形量沿齿宽和齿高方向均改变。在齿轮的顶角部和底角部修形量最大,修形量沿齿高和齿向2个方向同时缩小,修形曲面与齿面相交于一条直线,在齿面对角修形包含的基本设计参数见图2。
其中CEa为齿顶角修形量;dEa为齿顶修形起始直径;LEa为齿顶修形起始圆啮合线长度(渐开线展角);bEa为齿顶修形宽度;CEf为齿根角修形量;dEf为齿根修形起始直径;LEf为齿根修形起始圆啮合线长度(渐开线展角);bEf为齿根修形宽度[2]。
目前齿轮三维修形加工是在磨齿机上采用拓扑修形软件模块完成,修形齿面的建立是分别沿齿向和齿形2个方向划分网格,在网格节点上输入不同的修形量数值来表示不同修形曲面,如图3所示。

图 3 对角修形齿面网格划分Fig. 3 Triangular end modification face gridding
4 斜齿轮对角修形设计要点
在船用斜齿轮对角修形设计中总结出如下几个基本要点:
1)修形边界线平行于齿轮接触线
斜齿轮的接触线为一系列斜线,对于一个轮齿上来说,从一个角进入,接触线逐渐增长,然后再逐渐缩短,最后从对角退出。对角修形可修齿轮副啮入、啮出角位置,同时修形边界线平行于齿轮接触线,修形曲面与非修形曲面应圆滑过渡。
由啮合原理可知,在齿轮副啮合平面上,接触线与齿向均成基圆螺旋角,因此修形宽度与修形高度应满足如下基本要求:

式中:βb为基圆螺旋角。
2)同时啮合齿个数基本保持不变
由于齿轮传动重合度的影响,齿轮啮合过程中存在多齿少齿交替啮合现象,这就会使齿轮啮合刚度随时间发生变化,产生啮入啮出冲击。为避免此现象,经对角修形后,齿轮副在啮合周期内,最好使同时啮合轮齿个数基本保持不变。
3)齿轮副传动误差较小
最近国外许多研究表明齿轮啮合过程中的传动误差是影响齿轮箱振动噪声的主要因素之一,齿轮修形设计已偏重于减小齿轮传动误差上。齿轮传动误差是被动轮实际转角与理论转角之差,目前许多齿轮专用有限元分析软件如ANSOL,DU-GATES等均可进行齿面接触分析,得到齿轮副的传动误差。设计者可通过改变对角修形参数,使齿轮副传动误差较小。
5 算例分析
本文对一对船用斜齿轮进行分析,齿轮参数见表1。
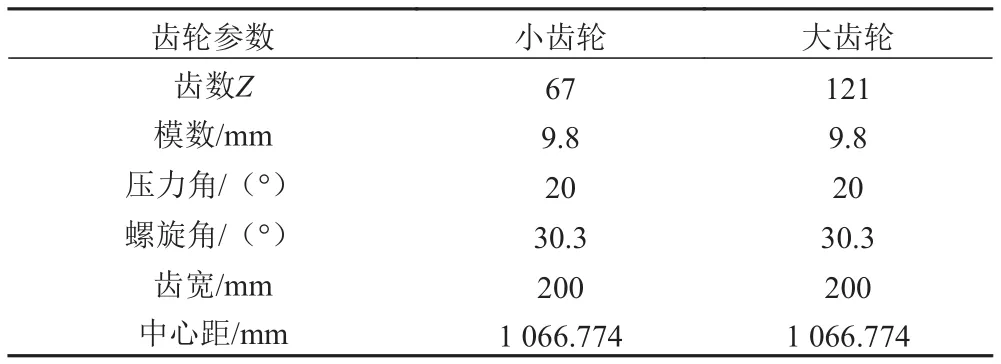
表 1 斜齿轮参数Tab. 1 Parameters of helical gears
本计算采用齿轮有限元ANSOL软件HELICAL3D部分进行分析。图4为建立的齿轮有限元模型。
图 4 齿轮有限元模型Fig. 4 Gear FEA modle
按照第1节提出的方法,根据上述要求,进行对角修形设计。斜齿轮设计后的对角修形参数见表2。

表 2 对角修形参数Tab. 2 Triangular end modification parameters
图5为修形前、后齿面接触印痕。由图可明显看出修形后在齿顶和齿根对角处的接触压力减小。

图 5 修形前后齿面接触印痕Fig. 5 Gear contact chart before and after flank modification
图6为修形前、后齿面接触载荷随时间的变化情况,计算所取时间间隔 6×10–5s,从 0.000 5~0.002 3 s,共计算1.8×10–3s,大于一个单齿啮合周期(单齿啮合周期 T=1.07×10–3s)。由图可见,未修形齿轮副存在同时5齿到6齿,6齿到5齿交替啮合过程,这种交替啮合,产生了齿轮刚度的变化。经对角修形后齿轮的齿67退出啮合的瞬间(6×10–5s以内)齿5刚好进入啮合,保证了齿轮同时啮合的轮齿个数始终为5个同时,齿轮的接触应力水平也较低。
图7为修形前、后齿面传动误差曲线,由图可见未修形传动误差 TE=2.479×10–6rad,对角修形传动误差TE=1.854×10–6rad。经对角修形传动误差减小 25%。
6 结 语
本文提出斜齿轮对角修形设计要点,并利用ANSOL软件HELICAL3D部分进行分析,得到的结论如下:
1)经适量的对角修形,可明显减小斜齿轮的齿面接触应力和传动误差。
2)考虑到齿轮箱加工误差,建议在对角修形的基础上可适当附加其他修形方式,以进一步改善齿轮啮合。
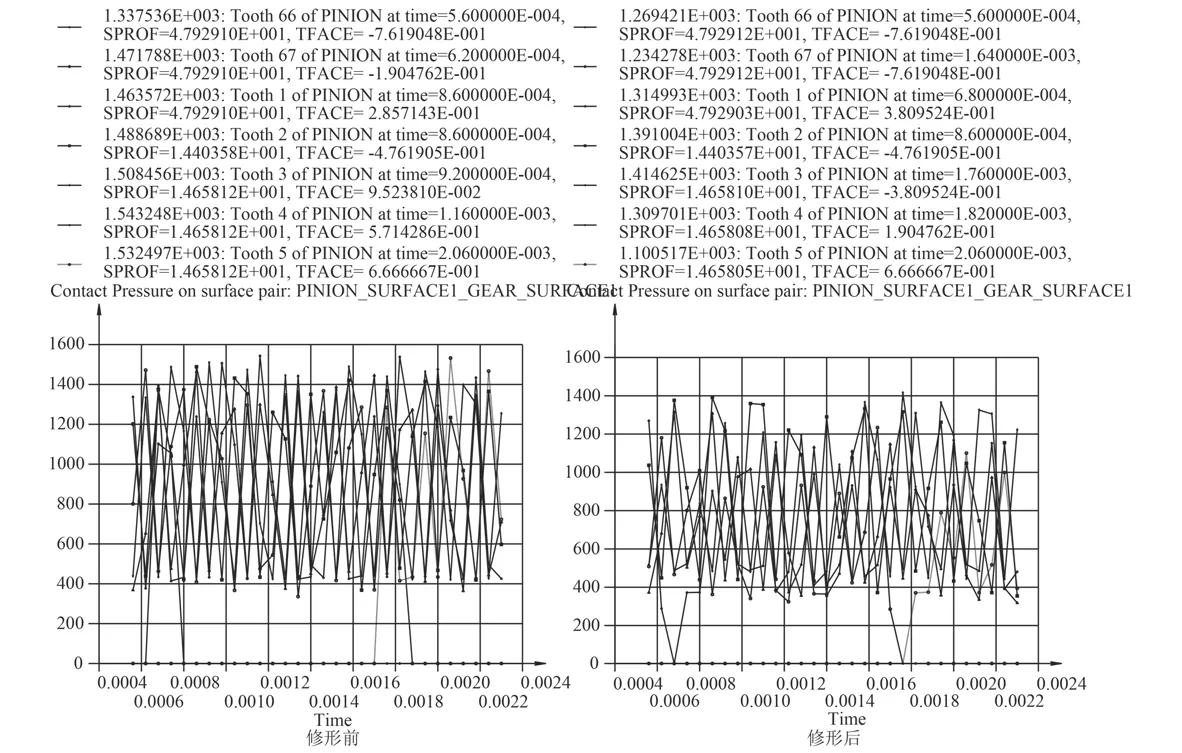
图 6 修形前后齿面接触载荷随时间变化Fig. 6 Gear contact stress before and after flank modification

图 7 修形前后传动误差Fig. 7 Transmission error before and after flank
[1]WALKER H. Gear tooth deflection and profile modification[J].Engineer. 1938,166: 434–436.
[2]BAHK CJ,PARKER RG. Analytical investigation of tooth profile modification effects on planetary gear dynamics [J].Mechanism and Machine Theory,2013,70: 298–319.
[3]BS ISO 21771: 2007 《Gears-Cylindrical involute gears andgear pairs-Concepts and geometry》.

