浮动渐开线花键微动损伤及磨损疲劳预测

肖立, 徐颖强, 陈智勇, 孙谢文, 徐颢

(西北工业大学 机电学院, 陕西 西安 710072)

浮动渐开线花键广泛应用于大扭矩、高转速的航空动力传输系统中，例如在航空发动机涡轮与压气机之间的动力联接、直升机主减速器行星传动及其与尾传动的动力耦合传递。区别于一般渐开线花键的定心方式，浮动花键齿面之间有间隙，内外齿顶及相邻齿根之间有间隙，并使用与侧隙相匹配的齿廓。这种非定心联接允许在运行过程中花键轴与花键套之间有一定的角向和轴线位移，以此来补偿制造、装配误差以及发动机或直升机启停和变工况运行的稳定性[1]。

正常情况下，渐开线花键的花键轴和花键套的轴线重合，在同一基圆上形成的齿具有相同的渐开线，此时所有的配对齿廓同时进入啮合，而与键齿的间隙无关。然而，浮动特征的存在使得花键轴与花键套之间有一定的不对中量，此时花键齿的接触状态发生改变，即具有较小侧隙的齿对先啮合，其余齿随侧隙的逐渐增大而依次啮合，直到所有载荷被分配完为止。在运动过程中，相对静止内/外花键齿面在交变载荷作用下产生接触应力和微幅振动，而微幅振动使得接触齿面产生相对运动，从而引起花键副的微动磨损。这种位置因素、几何因素造成的非正常接触使得载荷传递过程中并非所有的配合齿对都接触，增大了花键齿面服役过程中过早发生磨损或疲劳的风险，大大降低了传动系统的可靠性和服役寿命。

对此，国内外学者展开了一些研究。Leen等[2-3]通过实验分析了循环载荷下的花键副低周疲劳、微动疲劳以及微动磨损之间相互作用的疲劳行为。Wavish等[4]开发了一种模拟花键微动接触的多轴疲劳实验装置，为分析花键微动疲劳失效行为及寿命预测提供了技术支撑。Ding等[5]基于临界面SWT损伤准则和Ruiz损伤参数，预测并分析了花键副的微动疲劳，建立了考虑花键滑移效应的SWT修正模型。薛向珍等[6-7]在SWT预估疲劳寿命基础上引入修正的Archard模型，考虑了微动过程中的磨损效应，给出了渐开线花键微动磨损-疲劳寿命预估方法。为探究浮动特征对花键副的影响，赵广等[8]建立了不对中花键-转子系统动力学模型，分析了不对中对转子系统的振动特性。Medina等[9]基于边界元法分析了角向偏心花键的齿面接触压力和滑移的演化。Hong等[10]基于有限元法分析了不对中花键的齿面接触载荷分布。Curà等结合所开发的角度不对中花键副试验装置[11]，开展了角向不对中花键副齿面载荷特性、微动损伤以及微动磨损预测等[12-14]方面的实验及理论研究。胡正根和陈元等[15-16]通过有限元法分析了角向不对中花键的齿面接触应力和相对滑移分布，并探讨了齿面摩擦功和微动损伤参数的分布规律。谭援强和蒋理宽等[17-18]基于有限元法分析了角向不对中、径向不对中以及角向与径向不对中共同存在下的齿面接触压力及齿间载荷的分布规律，同时结合Ruiz损伤参数对一般渐开线花键齿面微动磨损的进行了预测与评估[19]。胡娟娟等[20]通过适当的齿廓修鼓减轻了角向不对中花键的齿面应力集中现象，从而改善了齿面接触状况。然而，浮动特征产生的轴线不对中以及角向偏心改变了花键齿面接触状态，对齿面微动磨损及损伤具有明显的影响，对此类花键副的齿面损伤及疲劳寿命预测却鲜有文献提及。

为此，本文建立了浮动花键有限元模型，分析了轴线不对中和角向偏心对花键副接触压力分布的影响规律，基于Ruiz损伤参数分析了轴向不对中和角向偏心对齿面Ruiz微动损伤参数值的分布，同时基于能量耗散模型和临界面SWT模型，建立了考虑磨损效应的花键齿面微动磨损-疲劳模型，分析了轴线不对中和角向偏心对花键齿面的微动磨损疲劳参数的影响，为浮动花键寿命预估提供一定基础。

1 浮动渐开线花键微动损伤及磨损疲劳预测模型

1.1 Ruiz微动损伤综合参数法

Ruiz等人在研究燕尾榫结构微动疲劳损伤时首次提出了Ruiz准则[21]，即：

RFDP=δμp

(1)

式中：δ为相对滑移距离;μ为摩擦因数;p为接触压力。

该参数描述表面剥离损伤的微动行为,即由粘着引起的微动表面损伤,接触表面的微幅滑移导致附着物的脱落,最终导致表面剥离。但该参数只能对裂纹位置进行大概预估,不能解释在拉应力和压应力下的裂纹成核倾向。Vidner等[22]在Ruiz参数的基础上提出了Ruiz微动损伤参数，在本文中被用来评估花键齿面的微动损伤,即

RFFDP=σTδμp

(2)

式中，σT为切向拉应力。RFFDP参数将微动疲劳简化为单轴疲劳,认为疲劳裂纹的扩展是由切向正应力决定,并在RFFDP值最大处裂纹开始萌生。

1.2 考虑磨损效应的花键副临界面SWT疲劳损伤模型

1.2.1 基于能量耗散的浮动花键微动磨损模型

工程上,Archard粘着模型[23]和能量模型[24]被广泛用来预测微动磨损过程。然而Archard模型无法考虑接触表面摩擦因素的变化对磨损过程的影响。考虑到花键副磨损过程中齿面接触几何变化的复杂性和不确定性,基于能量观点将花键材料的磨损看作能量的消耗与转化,进而不受齿面滑移幅值和摩擦因数变化的影响,使得齿面磨损预估更准确。

能耗法定义磨损量与磨损体积之间关系为

V=α∑Ed

(3)

式中:V为磨损体积;α为能量耗散系数;Ed为接触表面的摩擦能密度,在不考虑能量损失的情况下,摩擦能密度等效于在相对滑移δ上剪切力Q所做的摩擦功,即:Ed=Q·δ。

在有限元模拟中,接触面上材料的迁移或去除的磨损模拟是通过局部接触域的节点坐标移动实现的。局部接触节点(x)在特定时间t的增量磨损深度Δh(x,t)可以计算为

Δh(x,t)=αsq(x,t)Δs(x,t)ΔN

(4)

微动磨损的模拟是基于Abaqus二次开发完成的,通过Fortran语言编写的Umeshmotion子程序提取齿面上接触点的剪切力、相对滑移等参数,依据上述修正的耗散能量磨损模型(见公式(4))计算出每一载荷循环下的磨损增量。花键齿面的接触几何变化是通过任意的拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)自适应网格技术来实现依赖于磨损增量变化的节点坐标更新。

1.2.2 临界面SWT疲劳损伤模型

常见的描述材料的多轴疲劳损伤主要有应力(应变)法[26]、能量法[27]以及临界平面法[28]等,其中临界平面法定义裂纹总是沿着特定平面萌生并扩展,也就是说,裂纹扩展的方向和速度取决于临界面上的损伤参数,通过选择临界平面上的应力或应变分量作为疲劳损伤参数从而建立疲劳寿命模型来预测材料的疲劳寿命。目前,Fatemi-Socie(F-S)模型[29]和SWT模型[30]被广泛用于描述微动过程的裂纹成核位置、传播方向和疲劳寿命。其中,F-S模型认为临界平面上的剪切应变主导裂纹萌生,最大法向应力驱动裂纹的扩展。然而,参考文献[31]指出,微动引起的花键疲劳损伤主要为拉伸裂纹破坏(I型裂纹)。因此,取决于临界平面的法向应力和应变的SWT模型被选择来描述浮动花键的疲劳行为,其以最大法向应变幅值的平面为临界面,损伤参数包括最大主应变幅值和最大主应变垂直面的最大法向应力,即

(5)

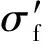
微动磨损引起的材料去除和迁移对花键齿面接触区域中的应力重新分布具有重大影响,通过疲劳损伤的累积更合理地描述这种应力场随循环载荷变化而变化情况下的损伤。通常用于描述线性疲劳累积的Palmgren-Miner(P-M)准则被修改为

(6)

在有限元中,累积损伤是基于每个微动循环中单元积分点处的应力和应变来计算的。然而由ALE技术驱动以实现消除材料磨损的网格更新可能会导致前后微动循环的单元积分点位置不一致,从而可能产生错误的累积损坏。使用Madge等[32]提出的材料点网格(MPM)方法来解决这个问题。其定义了独立于有限元网格的固定节点坐标,并结合了线性插值计算MPM中节点累积损坏来消除已移除的节点,从而考虑了磨损对累积疲劳损伤的影响。因此,所建立的考虑磨损效应的浮动花键副微动疲劳预测流程如图1所示。

图1 考虑磨损效应的浮动花键齿面微动疲劳预测模型

2 浮动渐开线花键副的齿面接触分析

2.1 浮动渐开线花键副有限元模型

浮动花键副的键齿啮合类型如图2所示,主要包括对中、轴线不对中和角向偏心3种,定义花键副的全局坐标系为O-XYZ,内、外花键副坐标系分别为O-XmYmZm和O-XnYnZn。为便于说明不对中对每个齿面的接触载荷分配的影响,对外花键键齿按图2a)进行编号。同时轴线偏移量e、角向偏心量β分别按图2b)进行调整。本文选用的花键副材料为航空高强钢18CrNi4A,弹性模量E=210 GPa,泊松比υ=0.3,密度ρ=7 800 kg/m3,花键副的几何参数如表1所示。

图2 浮动花键副啮合类型

表1 花键副几何参数

通过有限元进行接触分析,建立的花键副全齿啮合模型如图3所示。角向偏心下的内花键的轴线(黑色虚线)与外花键的轴线(红色虚线)存在一定的轴夹角。L表示齿宽,a表示啮合面高度,为便于描述齿面位置,定义齿面上任意一点沿轴向距齿端的距离为x,齿廓方向任意一点与啮合面起点距离为y。在有限元模型中,采用结构化网格方式,定义单元类型为C3D8R,且对花键的齿面进行网格密化,整个模型共计338 400个网格,其中花键齿细划分了288 000个网格单元,划分结果如图3b)所示。主-从面接触算法用于定义花键齿的接触对,其中选择内花键齿面为“主面”,外花键齿面为“从面”,并在接触属性中选择切向行为为各向同性的库伦摩擦,摩擦因数设置为0.28,法向行为设置为“硬”接触,采用有限滑移算法。施加边界条件时,将内、外花键除绕轴旋转外的其余5个自由度全部约束,外花键施加转速,而内花键施加反方向的负载扭矩,并将负载由内花键传递到外花键。考虑到航空传动变工况、多激励的载荷特征,假设花键传递载荷以简谐波形式进行变化,即

T(t)=kvTm[1+εcos(ωnt+φ)]

(6)

式中:kv为动载系数;Tm为平均传递扭矩;ε为输出扭矩幅值波动系数;ωn为啮合频率;φ为啮合相位角。

图3 浮动花键有限元模型

2.2 轴线不对中下的齿面接触压力分布

图4为平均传递扭矩为3 000 N·m时的3种轴线不对中量下各齿面最大接触应力云图,齿面接触状态分布与文献[16]基本一致。在轴线不对中e=0.01 mm时,花键各齿面最大接触应力的变化较为平缓,最大接触应力波动幅值为16.9 MPa,且各齿面分担有载荷。在轴线不对中e=0.03 mm时,花键各齿面最大接触应力分配较为不均,最大接触应力波动为50.8 MPa,而第8～12号齿齿面最大接触应力较小,第24号齿附近的各齿面承受较大的接触应力。在轴线不对中e=0.06 mm时,花键各齿面最大接触应力分配较为不均,最大接触应力波动为97.5 MPa,且第7～13号齿几乎不承受载荷,而24号齿附近各齿齿面亦承受较大接触应力。随着轴线不对中的增大,各齿面最大接触应力分布更为不均,即齿面接触承载状态更为恶劣。

图4 不同轴线不对中下的花键各齿面最大接触应力

图5为3种不同轴线不对中量下的第24号齿的齿面不同位置处的接触应力分布。在图5a)中,相较于e=0.01 mm的齿面齿顶接触应力,e=0.03 mm和e=0.06 mm的花键齿顶最大接触应力分别高出49.7%和129.9%。在齿中位置(见图5b))处,相较于e=0.01 mm齿面接触应力,e=0.03 mm和e=0.06 mm的花键齿中最大接触应力分别高出50%和128.6%。而在图5c)的齿根位置处,较于e=0.01 mm齿面接触应力,e=0.03 mm和e=0.06 mm的花键齿根最大接触应力分别高出65.2%和167.7%。同时3种不同轴线不对中花键均在两端处存在应力集中现象,即x/L=0和x/L=1处出现较大的接触应力,且轴线不对中量越大,齿面接触应力越大。轴线不对中的存在,使得花键齿面承载变得更为严重,进而有可能加剧齿面的磨损或损伤进程,使得花键过早发生失效。

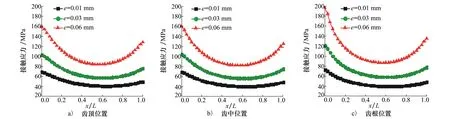
图5 轴线不对中下的齿面沿轴向不同位置接触应力分布

图6分析了第24号齿在x/L=0处,3种不同轴线不对中花键沿齿高方向的接触应力分布。沿齿高方向,齿面接触应力先增大,并在齿根位置y/a=0.08处达到最大,之后沿齿高方向缓慢减小。同时,相较于e=0.01 mm的花键齿面接触应力,e=0.03 mm和e=0.06 mm的花键y/a=0.08与y/a=1的接触应力变化幅值分别高出325.2%和804.3%,说明随着轴线不对中量的增大,花键沿齿高位置的接触应力变化趋势更为明显。

图6 轴线不对中下的花键齿沿齿高方向接触应力

2.3 角向偏心下的齿面接触压力分布

图7为3种角向偏心下的各齿面最大接触应力云图分布,其各齿面的接触应力分布与文献[16]基本吻合。不同角向偏心下的花键出现2个峰值接触应力(10,25号齿),其中在第10号齿处的最大接触应力值大于第25号齿的最大接触应力值。在β=0.06°时,花键各齿齿面最大接触应力波动较为平缓,波动幅值为37.5 MPa。在β=0.10°时,花键各齿齿面最大接触应力波动幅值为74.6 MPa。在β=0.20°时,花键各齿齿面最大接触应力波动较为明显,波动幅值达178.5 MPa。且在传递相同载荷的条件下,角向偏心越大,各齿面最大接触应力较大,即角向偏心的增大使得花键各齿面有效接触面积变小,进而在齿面产生的应力集中效应更为明显。

图7 不同角向偏心下的花键各齿面最大接触应力

图8为是3种不同角向偏心下的第10号齿和第25号齿的齿面齿根位置沿轴向接触应力分布。由图可知,角向偏心的存在使得不同齿的接触状态发生了变化。在10号齿面上x/L=0处几乎没有发生接触,接触应力从x/L=0处到x/L=1处逐渐增大,且在x/L=1处达到最大。在x/L=0～0.725处,花键齿面接触应力随角向偏心量的增大而减小,而在x/L=0.725～1处,齿面接触应力随角向偏心量的增大而增大。同时齿面沿轴向的接触应力增长率随角向偏心量的增大而增大。而25号齿的齿面接触应力在x/L=0处为最大,从x/L=0到x/L=1齿面接触应力逐渐减小,且在x/L=1处齿面几乎不发生接触。在x/L=0～0.275处,角向偏心量越大,花键齿面接触应力越大,而在x/L=0.275～1处,齿面接触应力随着角向偏心量的增大而减小。同时,齿面沿轴向的接触应力下降率随角向偏心量的增大而增大。角向不对中的存在改变了齿面的接触状态,使得花键齿仅在一端发生接触,且随着角向偏心量的增大,齿面接触应力集中现象更为明显,加剧了花键的边缘接触效应。

图8 角向偏心下的齿面沿轴向不同位置接触应力分布

图9为3种不同角向偏心下的花键第10号齿在x/L=1处沿齿高方向的接触应力分布。由图可知,在y/a=0～0.08处,齿面接触应力急剧增大,且在y/a=0.08处达到齿面最大接触应力。在y/a=0.08～0.75处,齿面接触应力缓慢减小,之后y/a=0.75～1处齿面接触应力又呈小幅上升趋势。同时随着角向偏心量的增大,这种变化趋势更加明显。角向偏心的存在加剧了齿面接触不均现象,使得承载边缘化效应更加严重,而这对花键的使用和维护是极为不利的。

图9 不同角向偏心下的花键齿沿齿高方向接触应力分布

3 浮动渐开线花键的齿面微动损伤及磨损疲劳

3.1 基于Ruiz损伤参数的浮动花键齿面损伤

图10为3种轴线不对中量下的花键各齿面最大Ruiz微动损伤参数RFFDP值的分布。可以发现,在3～19号齿附近齿面最大RFFDP值较小,且随着轴线不对中量的增大,该处齿面最大RFFDP值降低,主要是由于该处的齿面接触承载随着轴线不对中的增大而减小,且e=0.06 mm花键的部分齿面几乎不承载,因此齿面微动损伤程度较小。而第24～28号齿附近的齿面存在较大的RFFDP值分布,且最大RFFDP值出现在26号齿面上,这与最大接触应力发生在24号齿面(见图4)有些差异,主要是由于该处齿面相对滑移较大。同时,相较于e=0.01 mm齿面,e=

图10 不同轴线不对中量的花键各齿面最大RFFDP分布

0.03 mm和e=0.06 mm齿面最大RFFDP值分别高出203.9%和870.7%,说明轴线不对中量的增加,明显增大了键齿面的微动损伤程度。

图11为3种不同轴线不对中下的第26号齿齿面Ruiz损伤参数分布。3种不同的轴线不对中量的花键齿面沿x方向RFFDP值呈现“抛物线”状,即在齿面两端的可能产生较为严重的微动损伤,且x/L=0处的RFFDP值始终比x/L=1处大。同时,在x/L=0处沿y方向RFFDP值也呈现“抛物线”状,即在(x/L=0,y/a=0.16)和(x/L=0,y/a=1)处存在2个RFFDP峰值。图11a)中,e=0.01 mm的花键齿面在(x/L=0,y/a=0.16)的RFFDP值比(x/L=0,y/a=1)处高出2.3%,e=0.03 mm的花键齿面(见图11b))在(x/L=0,y/a=0.16)的RFFDP值比(x/L=0,y/a=1)处高出10.9 %,而e=0.06 mm的花键齿面(见图11c))在(x/L=0,y/a=0.16)的RFFDP值比(x/L=0,y/a=1)处高出约23.1%。随着轴线不对中量的增大,齿面最大损伤参数越大,说明轴线不对中的增加,明显增大了键齿面的微动损伤程度。

图11 不同轴线不对中下的齿面RFFDP参数分布

图12为3种角向偏心下的花键各齿面最大Ruiz微动损伤参数RFFDP值的分布。可以发现,各齿面最大RFFDP值的分布与齿面最大接触应力分布(见图7)较为相似,均呈“双峰”状分布。随着角向偏心量增大,两RFFDP峰值差分别为30.5,71.42和224.0。同时,相较于β=0.06°的齿面,β=0.10°和β=0.20°的齿面最大RFFDP值分别高出约167.2%和971.3%,说明角向偏心的增大加剧了齿面的微动损伤程度。

图12 不同角向偏心量的花键各齿面最大RFFDP分布

图13为3种不同角向偏心下的第10号花键齿齿面Ruiz损伤参数分布。可以明显看出,3种角向偏心的齿面的RFFDP值均沿x方向增大,呈现“指数增长”趋势,并在x/L=1处达到最大。同时,齿面在x/L=1处的RFFDP值呈现“抛物线”状,在(x/L=1,y/a=0.16)和(x/L=1,y/a=1)出现2个峰值,且(x/L=1,y/a=0.16)为齿面最大RFFDP值处。其中,β=0.06°的花键齿面在(x/L=1,y/a=0.16)的RFFDP值比(x/L=1,y/a=1)处高出6.9%,β=0.10°的花键齿面在(x/L=1,y/a=0.16)的RFFDP值比(x/L=1,y/a=1)处高出约10.6%,β=0.20°的花键齿面在(x/L=1,y/a=0.16)的RFFDP值比(x/L=1,y/a=1)处高出约20.8%。相较于β=0.06°的齿面,β=0.10°和β=0.20°的齿面最大RFFDP值分别高出约169.1%和1048.7%。角向偏心的存在可能使得花键齿在一端发生微动损伤,且其对齿面的微动损伤影响可能更为明显。

图13 不同角向偏心下的齿面RFFDP参数分布

3.2 浮动花键微动磨损-疲劳寿命预测

基于1.2节的所提出的预测模型,计算得到不同轴线不对中花键齿面疲劳累积损伤分布如图14所示。可以发现,x/L=0处存在齿面最大疲劳累积损伤,即存在明显的应力集中现象。随着载荷循环的增大,齿面累积损伤逐渐增大,而累积微动损伤增长率却反而降低,说明磨损效应能抑制疲劳裂纹的萌生和扩展。轴线不对中量为e=0.01 mm花键齿面随x/L增大,齿面累积损伤D逐渐降低,在x/L=0处基本没发生损伤。e=0.03 mm的花键齿面随x/L增大,齿面累积损伤D先逐渐降低,并在x/L=1附近有上升的趋势。而e=0.06 mm的花键齿面随x/L增大,齿面累积损伤D先逐渐降低,并在x/L=1附近有小幅增大。e=0.06 mm的花键在载荷循环N=98 000时,齿面最大累积损伤值接近于1,即发裂纹萌生。而此时,e=0.01 mm和e=0.03 mm花键齿面最大累积损伤值分别低出约99.1%和91.1%。说明轴线不对中的增大,加剧了花键磨损疲劳损伤进程,不利于花键的实际服役耐久性的提高。

图14 不同轴向不对中量的齿面疲劳累积损伤分布

同理,不同角向偏心花键齿面疲劳累积损伤分布如图15所示。不同于轴线不对中花键,x/L在0～0.9附近的齿面损伤值基本接近于0,即不存在损伤,而在x/L=1处齿面累积损伤值最大,即存在明显的应力集中现象,这与角向偏心花键齿面的局部边缘接触有关。随着载荷循环的增大,齿面累积损伤值增大,而累积损伤增长率却反而降低,这同样说明齿面磨损能抑制疲劳裂纹的萌生和扩展进程。同时,β=0.06°和β=0.1°花键在N=144 000次载荷循环下的最大损伤累积值分别为0.030 65和0.171 24,而β=0.2°花键在载荷循环N=20 000次附近齿面最大累积损伤就已接近于1,说明角向偏心亦促进齿面的疲劳裂纹萌生。

图15 不同角向偏心量的齿面疲劳累积损伤分布

表2为不同不对中参量的花键齿面磨损疲劳寿命预测,可以发现轴线不对中花键齿面裂纹萌生位置在x/L=0处附近,而角向偏心花键齿面的裂纹萌生位置发生在x/L=1处附近,且随着轴线不对中或角向偏心量的增大,齿面磨损疲劳寿命急剧下降。

表2 浮动花键副预估寿命

4 结 论

1) 轴线不对中使得各齿面接触分布不均,部分齿承载较大载荷,而部分齿几乎不承载。而角向偏心的存在改变了齿面的接触状态,使得花键齿仅在一端发生边缘接触效应。且随着不多中和偏心量的增大,这种现象更为明显。

2) 轴线不对中量的最危险花键齿面沿x方向RFFDP值呈现“抛物线”状,即在齿面两端可能产生较为严重的微动损伤,而角向偏心最危险齿面RFFDP值均沿x方向增大,呈现“指数增长”趋势,并在x/L=1处达到最大。

3) 轴线不对中花键齿面裂纹萌生位置在x/L=0处附近,而角向偏心花键齿面的裂纹萌生位置发生在x/L=1处附近,且随着轴线不对中或角向偏心量的增大,齿面磨损疲劳寿命急剧下降。