超空泡航行体高速入水空泡与载荷特性数值分析
鱼怡澜, 施瑶, 潘光, 车沛锜
(1.西北工业大学 航海学院, 陕西 西安 710072;2.西北工业大学 无人水下运载技术重点实验室, 陕西 西安 710072)
超空泡航行体通过在水下航行时产生包裹航行体的超空泡来减少航行体沾湿面积,使航行体所受阻力大幅降低,随着现代战争对水下武器快速性要求的提高,超空泡航行体的应用需求与日俱增。同时,为增大航行体航速与航深,需要发展更高效的发射平台,空投方式相比于水面舰艇或水下潜艇投放有攻击时间短、命中率高的优点。但空投航行体高速入水瞬间气、水、航行体发生瞬时强烈流固耦合作用,航行体承受瞬时极端载荷,流场出现复杂湍流流动与涡旋现象,可能引发航行体结构断裂、连接失效、弹道失稳等,直接影响着航行体入水的结构安全、弹道稳定以及航行体入水后产生的超空泡,从而影响航行体航行质量。因此,捕捉空泡界面演变规律,预报载荷峰值脉宽等对提高航行体速度、保证航行体安全入水有重要意义。
目前已有的超空泡航行体相关研究对象主要为速度低于100 m/s的圆柱体、楔形体、小球入水和直径小于0.01 m的射弹。其中,理论研究大多将问题简化处理,只能用于解决简单问题;实验研究中水洞实验不关心入水过程[1-3],高速射弹实验[4-5]由于设备条件限制很难将入水速度提高至100 m/s以上量级;数值仿真方法随着计算机技术的发展逐渐成为研究入水问题的重要手段[6-11],但目前对于高速超空泡航行体入水问题的研究仍然较少,而航行体高速入水问题的空泡流场更复杂、载荷与速度平方成正比,因此小型低速入水问题的结论不具备普适性,急需开展相关研究。
入水速度V与入水角度θ是影响空泡与载荷特性的重要因素,本文建立了适用于超空泡航行体以100~300 m/s速度高速入水的数值模型,分析了入水速度与入水角度对入水空泡与载荷特性的影响,为超空泡航行体高速入水相关研究提供参考。
1 数值计算模型
本文使用FLUENT进行数值模拟,将航行体视为刚体,考虑水的压缩性,采用RANS模型、VOF多相流模型、标准k-ε湍流模型和Zwart-Gerber-Belamri空化模型建立了航行体高速入水数值计算模型,并通过UDF(user defined function)实现航行体六自由度运动。
1.1 控制方程
流体的运动遵循质量守恒定律、动量守恒定律和能量守恒定律,因而可以通过这3个定律建立流体的控制方程组。本文使用雷诺平均N-S方程方法,该方法将瞬时运动分解为脉动运动和平均运动2项,是目前应用最广泛的方法,其具体方程为:
1) 连续性方程:

(1)
2) 动量守恒方程
(2)
3) 能量守恒方程

(3)
式中:u为速度;ρm为混合物的密度;μm为混合物动力黏度。
1.2 湍流模型
为了使控制方程封闭,选择标准k-ε湍流模型,该模型适用范围广,收敛性好。其中,湍动能k的输运方程为
(4)
湍流耗散的输运方程为
(5)
1.3 多相流模型
对于存在多相流动的问题需要使用多相流模型,VOF模型适用于存在互不相融的流体的交界面的情况,因此本文使用VOF多相流模型,设置空气相为主相,液体为第二相,水蒸汽为第三相,通过求解单元内的值判断其相分布,满足

(6)
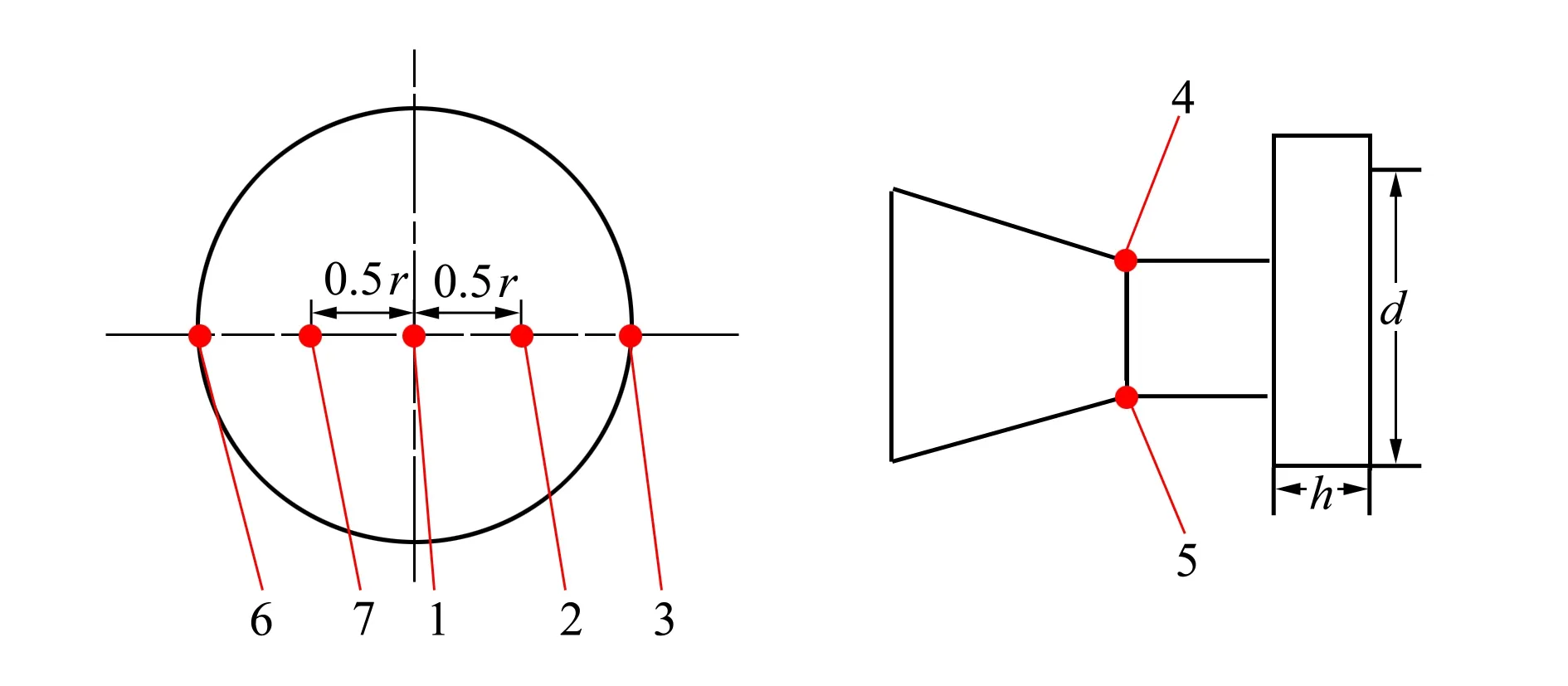
式中:ag=0时,该控制单元内无空气;ag=1时,该控制单元内全为空气;0 本文由于航行体高速入水存在空化现象,因此使用了Zwart-Gerber-Belamri空化模型,该模型基于Rayleigh-Plesset方程,其控制方程为 (7) 式中:气泡半径RB为1×10-6m;αnuc为汽化核心体积分数;汽化系数Fvap为50;凝结系数Fcond为0.001;pv为饱和蒸汽压力。 气相和水相的状态方程为控制方程提供了封闭条件。其中水相采用Tait状态方程,表示为 (8) p0和ρ0是参考温度T0下的参考值。K0和n是温度和压力的弱函数,通常假定它们为常数,分别是3×108Pa和7。 此外,将水蒸汽相和气相近似为理想气体 p=ρgRT (9) 式中:R为气体常数;ρg为气体密度。 航行体模型如图1所示,模型分为头部圆盘空化器、锥段、圆柱段,以空化器前端面圆心为坐标原点,航行体质量为M,总长为L,直径为D,质心距空化器端面距离为L1,空化器直径为D1,厚度为H,各尺寸如表1所示。 图1 航行体模型示意图 表1 航行体参数 计算域如图2所示,为长方体计算域,水域尺寸为27 m×27 m×40 m,空气域为27 m×27 m×10 m,坐标原点距左侧壁10 m。计算域上方为压力出口,其余均为壁面。航行体初始位置距水面0.01 m,地面坐标系原点位于航行体轴线与水面交点,入水角为航行体轴线与水平面所夹锐角。 图2 计算域示意图 本文使用重叠网格方案计算,背景域为六面体网格并加密航行体路径,重叠网格区域使用非结构化网格,两者交界处网格尺寸相同,网格如图3所示,总网格量约为8×106。 图3 网格示意图 为验证数值方法的准确性,在西北工业大学无人水下航行器重点实验室进行了实验验证,实验模型直径为0.02 m,质量为10.8 kg,入水角度为45°,入水速度为100 m/s,实验装置示意图如图4所示,主要由空气炮发射、数据采集和高速摄像装置等组成,通过高压气体推动航行体加速。数据采集装置主要由加速度传感器、数据存储模块、数据解析软件等组成,高速摄像装置由空中高速相机、水下高速相机和水下照明灯等组成。图5为9 ms和18 ms时实验与数值计算空泡对比图,可得本文使用的数值计算方法和实验结果吻合较好,建立的数值模型可靠。 图4 实验装置示意图 图5 空泡轮廓对比图,左:实验,中:仿真 本文子域网格量为背景域网格量的20倍,因此通过改变overset边界的网格尺寸改变网格量。选择其尺寸为50,60,100,140 mm,计算入水角为90°、入水速度100 m/s时航行体速度变化与加速度变化,结果如图6~7所示,综合考虑计算资源与计算效率之后选择使用overset尺寸为100 mm的网格计算。 表2 网格方案 图6 不同网格尺寸下航行体速度随时间变化曲线 图7 不同网格尺寸下航行体加速度随时间变化曲线 图8为航行体以速度100 m/s、角度60°入水的空泡演变图。可得航行体入水过程中空泡经历了产生、膨胀、闭合、收缩4个阶段。 在空泡产生阶段,航行体高速撞击水面,使自由液面流动发生分离,将水排开使空气进入水中;在空泡膨胀阶段,空化器周围空泡壁面持续扩张,随着航行体入水深度增大,更多的空气进入水中,空泡长度逐渐增大;在空泡闭合阶段,首先空泡闭合在航行体上,使航行体表面沾湿,其次随着航行体入水深度增大,空泡长度增大,内部压力降低,流体对空泡的压力使空泡发生颈缩直至发生深闭合;在空泡收缩阶段,空泡分为上下两部分,上部分空泡逐渐向水面收缩直至闭合,下部分空泡随航行体运动,随着航行体入水深度增大持续收缩。 整个入水过程中航行体将自身动能转化为流场势能,流场将势能转化为水的动能,使流体从高压区流向低压区,同时使空泡演变。 图8 入水空泡形态随时间演变图 如图9所示,空泡最大直径dmax为航行体产生空泡的最大直径。图10为不同入水条件下空泡最大直径,可得随着入水速度增大,空泡最大直径增大,原因为速度增大使航行体动能增大,使液体流速增大,空泡扩张速度增大;随着入水角度的增大空泡直径变小。其中 λ=dmax/2D (10) 图9 空泡最大直径定义图 图10 空泡最大直径变化曲线 图11 不同速度下空泡随时间演变图(θ=90°) 图11为入水角度90°,入水不同速度入水空泡图,由图可得随着速度增大航行体空泡出现闭合的位置深度增大。原因为速度增大使动能增大,空泡中压力降低的速度变慢,因此空泡被夹断的时间推迟。 图12为100 m/s入水270 ms空泡轮廓图,4个入水角度下都发生了空泡深闭合,且发生深闭合时航行体航行距离相同,因此入水角度对空泡深闭合无影响。 图12 入水270 ms空泡轮廓图(V=100 m/s) 图13为不同角度入水加速度变化图,图中速度100 m/s下加速度出现2次峰值,第一次峰值是航行体入水瞬间冲击造成,在此处随入水角减小航行体头部与水面的接触面积减小,加速度相应减小。第二次峰值是由于空泡闭合在航行体上,使航行体表面沾湿,在此处随入水角减小加速度增大。 随着入水速度增大加速度峰值增大,出现时间提前,原因为速度增大使航行体动能增大,入水瞬间向周围的水传递的能量增大。 图13 加速度随时间变化曲线 为了使模型所描述的规律独立于量纲的影响,通常需要使用无量纲量来描述客观规律,因此将轴向载荷F通过(11)式无量纲化为轴向载荷系数Cd Cd=F/(ρwπD2V2) (11) 式中,ρw为水的密度,取1 000 kg/m3。 图14为不同角度入水时航行体轴向载荷随时间变化图,由图可得随着入水速度增大,轴向载荷峰值增大,出现时间提前。其原因为速度增大使航行体动能增大,向自由液面传递的能量增大。 随着入水角度减小,航行体受轴向载荷峰值逐渐减小。其原因为随着入水角减小航行体动能水平分量增大,垂直分量减小,两者轴向分量之和减小。 图14 入水轴向载荷系数Cd随时间变化曲线 图15为100 m/s,60°入水部分时刻压力云图,可得入水时空化器迎流面首先出现压力峰值,其次锥段出现峰值,之后航行体尾部及空泡深闭合处出现压力峰值,最后随着时间增大压力峰值面积增大且逐渐关于航行体轴线对称。 图15 不同时刻压力云图(V=100 m/s,θ=60°) 航行体表面压力峰值出现在触水区域,速度高于150 m/s时空泡包裹航行体,压力峰值只出现在空化器上,因此进一步研究空化器周围压力分布,设置了压力监测点如图16所示,其中r为空化器半径。 图16 监测点分布示意图 图17为200 m/s不同角度入水监测点压力随时间变化图,可得被空泡包裹的点4,5压力近似为0,远小于空化器迎流面压力;空化器表面点3,6的压力值小于点1,2,7,即空化器迎流面的压力越接近圆心越大;斜入水时,点3和点6的压力差较大,点2和点7的压力差较小,即空化器迎流面压力分布不对称,随着入水角度的减小不对称现象加剧,且沿着半径向圆心方向减弱。 图17 各监测点压力随时间变化曲线(V=200 m/s) 本文开展了超空泡航行体不同入水速度和入水角度下入水过程数值仿真,获得航行体空泡演变、尺寸、载荷及压力变化规律,获得结论如下: 1) 随着入水速度增大,空泡闭合位置的深度增大,空泡最大直径增大;随着入水角减小空泡最大直径增大,深闭合发生时间不变。 2) 100 m/s和150 m/s速度入水出现2次加速度峰值,随着入水速度增大加速度峰值增大;随着入水角减小,加速度第一次峰值减小,第二次峰值增大。 3) 随着入水速度增大,航行体轴向载荷峰值增大,出现时间提前;随着入水角度减小,轴向载荷峰值减小。 4) 入水过程中空化器迎流面压力沿着半径向圆心方向增大,但斜入水时的不对称现象减弱。1.4 空化模型
1.5 状态方程

2 计算模型与网格
2.1 航行体模型



2.2 数值方法验证
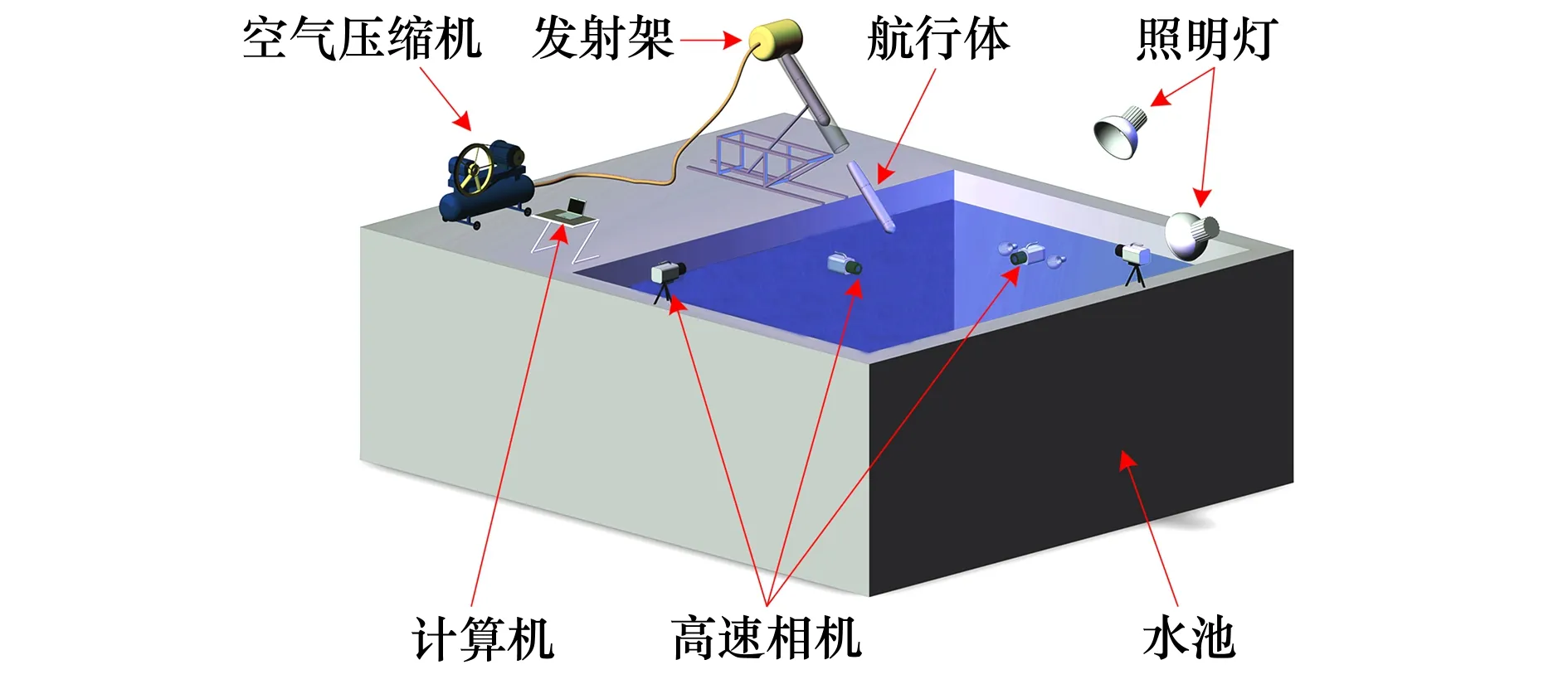
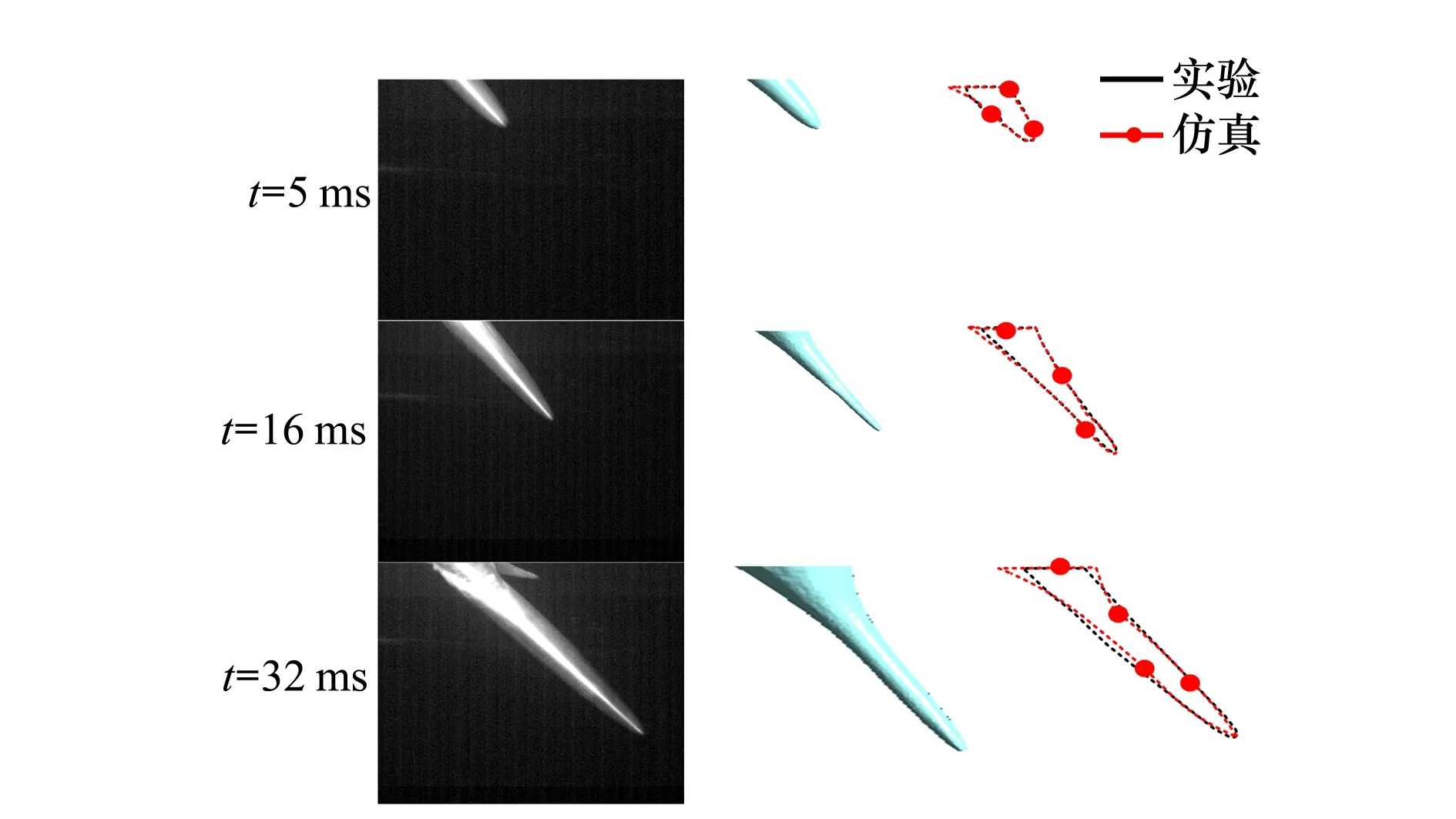
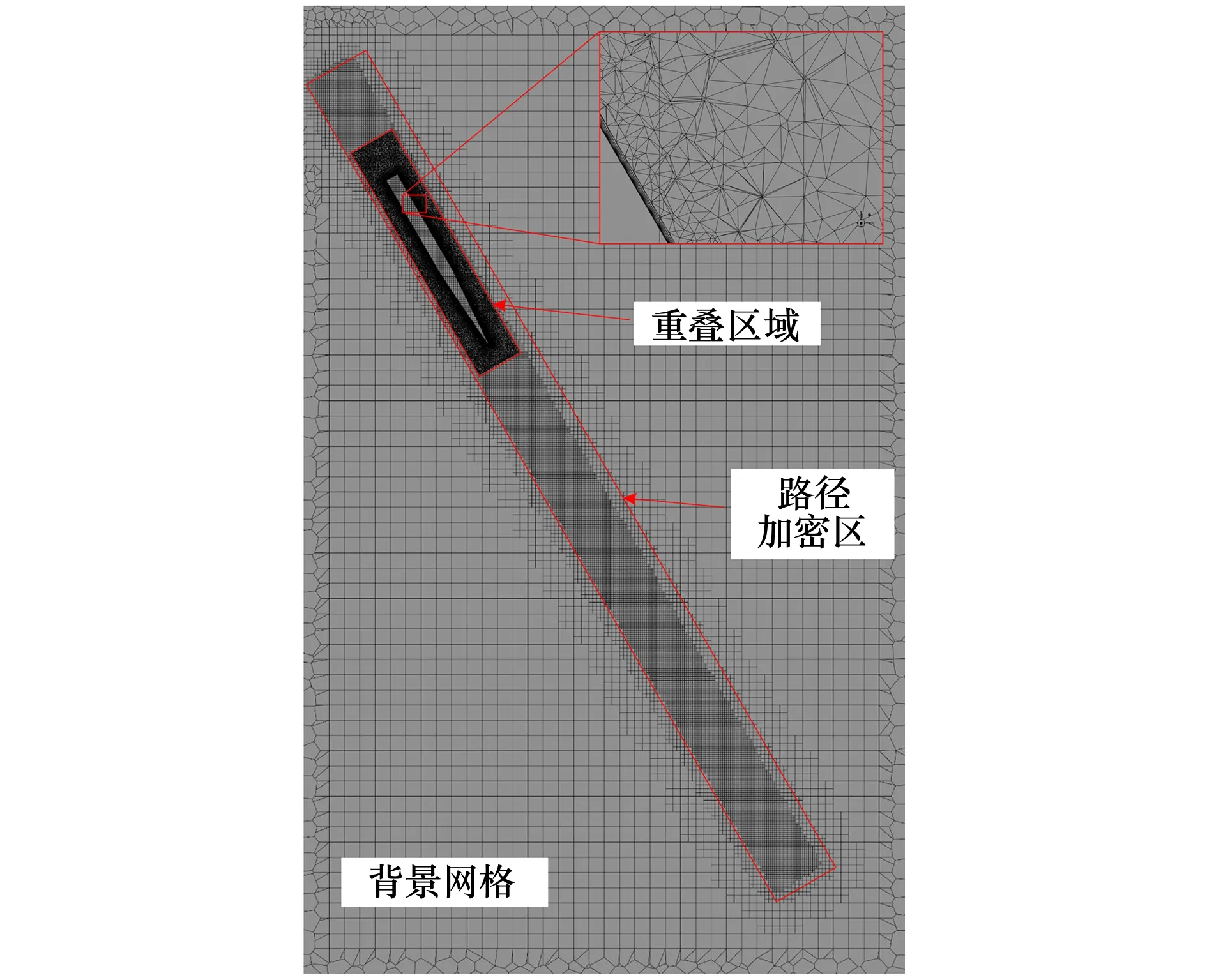
2.3 网格无关性验证

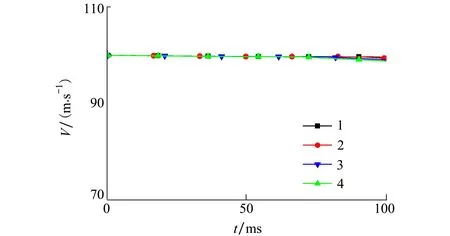

3 计算结果及分析
3.1 空泡特性研究



3.2 不同角度下载荷特性研究

3.3 不同速度下载荷特性研究
3.4 压力特性

4 结 论
——秒杀水阻力

