直刃刀具加工的面齿轮承载接触特性

彭先龙，徐琪超，乔心州

(西安科技大学 机械工程学院，陕西 西安 710054)

0 引 言

面齿轮具有重合度大、传动平稳且噪音小等特点[1]，主要用于汽车差速器、直升机主减速器等重要的传动系统中。传统上用插齿法定义面齿轮的理论齿面，因此面齿轮的各种加工方法，如铣齿、滚齿、磨齿[2-5]，都是对假想小轮(插齿刀)与面齿轮啮合过程的模拟。导致各种刀具必须以假想小轮渐开线作为产形线，若小轮的基本参数有稍许变化，就必须重新设计、制造、修整刀具，从而刀具的适用性、通用性较差，导致制造成本增加。

用产形线为直线的平面刀具或锥面刀具(统称为直刃刀具)加工面齿轮[6]，可以大幅提高刀具的通用性，加工各种规格的面齿轮。利用直刃刀具加工面齿轮有2种加工方法：其一为点接触双参数包络法[7]，利用刀具外缘加工面齿轮(其可行性已得到验证)，所加工的齿面与理论齿面完全相同，其加工效率与具有渐开线的碟形刀具加工面齿轮相当；其二为线接触单参数包络法[6，8-9]，利用刀具平面加工面齿轮，属于近似加工，为了综合直刃刀具运动规律，需要预设接触路径，由于用产形平面与被加工齿面的空间接触直线代替假想小轮与理论齿面的空间接触曲线，将引入一定的齿面偏差。因此近似齿面与理论齿面的几何接触特性、承载接触特性有所不同，在近似齿面建模和几何接触分析的基础上，进一步揭示近似齿面的承载接触特性就十分必要。

LTCA可以在一定程度上反映实际应用中的齿轮强度、动态品质等性能指标，广泛应用于齿轮传动设计中[10-11]。唐进元等人用赫兹接触应力确定面齿轮传动有限元分析模型的网格密度，考虑了多载荷对面齿轮传动承载特性的影响[12]。付学中等人基于自主开发的LTCA程序研究变位面齿轮传动的承载特性，并获得优化的变位系数[13]。LITVIN利用商用有限元软件研究多种面齿轮传动的强度特性，以及齿面修形对强度特性的影响[14-15]。BARONE等人基于曲面拟合研究齿面修形参数、安装误差对面齿轮承载特性的影响[16]。ZANZI提出一种面齿轮传动的齿面修形方法，并用商用有限元软件验证齿面修形对降低弯曲与接触应力的有益效果[17]。郭辉等人的LTCA结果表明蜗杆刀具抛物线修形可以有效降低面齿轮传动的边缘接触[18]。方宗德等人利用LTCA程序研究弧线齿面齿轮的承载接触特性，并考虑安装误差对强度的影响，表明弧线齿面齿轮强度高于直齿面齿轮[19]。

借鉴以上面齿轮传动的LTCA方法，对比直刃刀具线接触单参数包络法加工的面齿轮近似齿面与插齿法定义的理论齿面的承载接触特性的异同，分析预设接触路径、安装误差等因素对近似齿面承载接触特性的影响，以指明基于这种加工方法的面齿轮传动设计方向。

1 面齿轮近似齿面及TCA

表1所示为面齿轮近似齿面的传动参数，近似齿面的具体建模过程可以参考文献[8-9，20]。

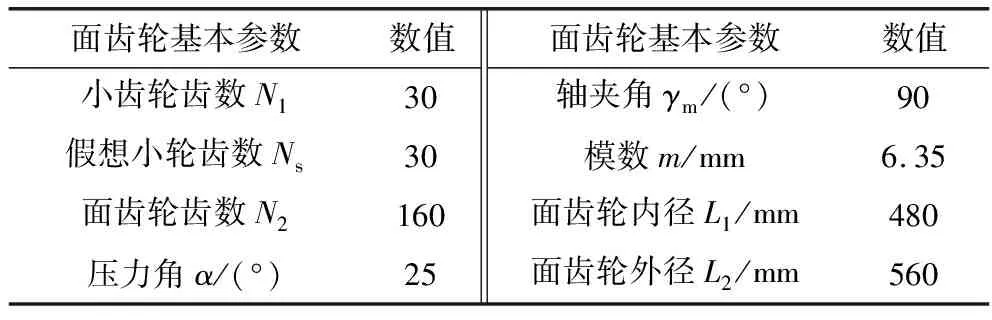
表1 面齿轮基本参数

为综合刀具运动规律，需先预设接触路径。如图1所示，cp为预设接触路径，L2p为平面刀具与近似齿面的接触线，cp的倾角由η表示，其参考点Fμ位置由Rμ，Lμ这两个参数控制[21]，3种算例的参数见表2。预设接触路径的具体计算过程可参考文献[9]，文中只就3种算例的承载接触特性进行讨论。

表2 预设接触路径参数

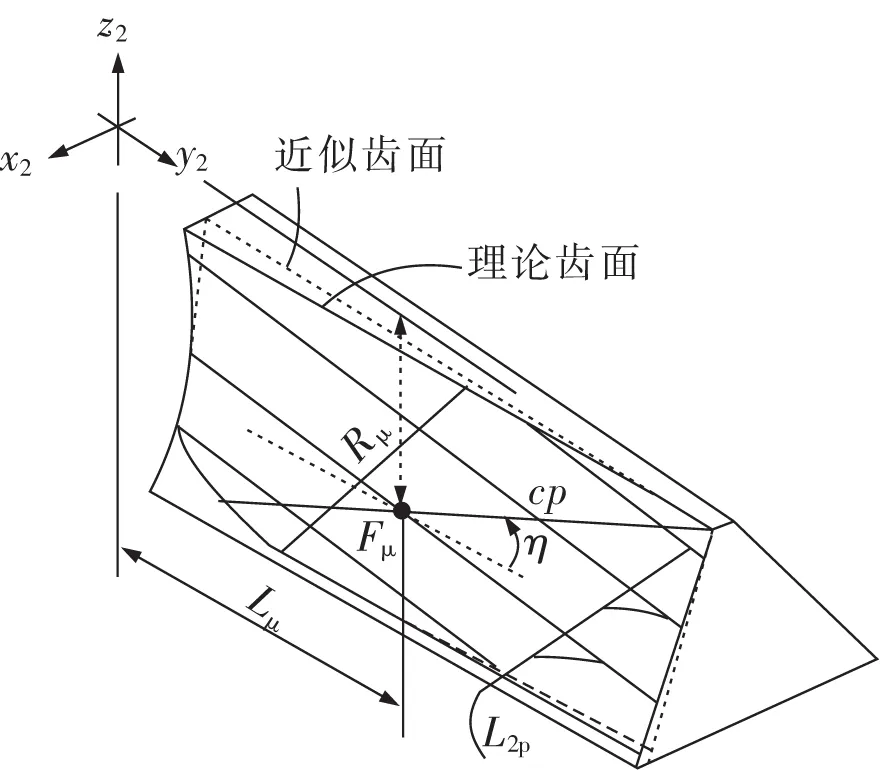
图1 近似齿面的预设接触路径

3种算例的参考点均位于齿面中央，算例a的预设接触路径是面齿轮传动修形齿面的常见接触路径，算例b，c是比较特殊的2种接触路径，分别沿齿面对角线接触和沿齿面节锥面接触。

根据预设接触路径综合刀具运动规律，确定直刃刀具加工的近似齿面，3种算例近似齿面如图2蓝线所示，红线为插齿法定义的理论齿面(假想小轮与小轮齿数相同)，3种算例对应的最小齿面偏差分别为-1.431，-1.097，-1.011 mm，最大齿面偏差均为0.000 mm。

图2 近似齿面与理论齿面之间的偏差及TCA接触路径

3种算例中的近似齿面与小轮渐开线齿面啮合的TCA接触路径如图2所示，齿面接触路径与预设接触路径基本一致，若考虑边缘接触情况，3种算例均存在边缘接触，算例a、b的边缘接触位于齿顶齿根，算例c的边缘接触位于大端小端。图3为3种算例的几何传动误差，齿面接触的传动误差接近于0″，边缘接触的传动误差较大，这与理论齿面和小轮渐开线齿面(假想小轮比小轮多1～3个齿)啮合的几何传动误差类似。

图3 几何传动误差

2 有限元前处理与后处理

2.1 有限元前处理

分别将面齿轮近似齿面(如图2所示)和小轮齿面离散点坐标变换到TCA固定坐标系Sf中，(其变换过程和坐标系参考文献[22])，从而在LTCA和TCA中可以考虑相同的安装误差且能保证微米级的齿面精度；按照某一接触点两齿面的转角φ1、φ2，在Sf中分别转动面齿轮和小轮接触齿面(对应下文观察齿对齿面)，对于另一侧齿面也做相应处理；分别在面齿轮和小轮的接触齿面、另一侧齿面之间利用绕各自轴线的坐标变换填充节点，形成单齿有限元节点；分别将面齿轮、小轮单齿有限元节点绕各自轴线旋转整数齿的转角，形成多齿有限元节点；根据ABAQUS关于八节点六面体单元的编写规则，分别对面齿轮、小轮多齿有限元节点依次编号，构建8节点单元并对其编号，形成多齿有限元网格模型。

设置前处理条件，分别如下：材料密度为7 800 kg/m3，泊松比为0.29，弹性模量为206.8 GPa；以TCA接触齿面同侧的齿面作为各齿对的主从接触面；将小轮内圆柱面和轮体两侧面网格点与其轴线上任意参考点RP-1固连，在该点施加1 600 N·m的扭矩并释放该点绕轴线的旋转自由度，将面齿轮底面和轮体两侧面网格点与其轴线上任意参考点RP-2固连并约束该点的所有自由度；选用静力学通用算法，分析步的时长为1 s；以接触应力、弯曲应力、角位移量、正应力为场输出量[23]。

通过编程软件将观察齿自啮入至啮出的每个接触点的网格模型、前处理条件等信息输出到单个inp文件，构成承载接触问题静态有限元计算的批处理文件，利用基于Windows的批处理程序将这些inp文件导入ABAQUS并提交计算，即可无人值守的完成计算过程。由图3可知，由黑点标记的观察齿对在啮入啮出时，其前后参与啮合的齿对仅有2对，因此采用5齿模型即可得到准确的计算结果。图4所示为算例a中某接触点的有限元装配示例模型。

图4 面齿轮传动的有限元模型

实际计算中齿高、齿宽和齿厚方向上的节点数分别为：51，81，7，总节点数为159 732，共计133 280个单元。

2.2 有限元后处理及结果

求解结束后，通过ABAQUS内嵌的Python语言编写脚本文件，可获得承载接触印痕、齿面接触应力、齿根弯曲应力、小轮角位移量，经适当处理可得载荷分布系数[11]、承载传动误差[12]。

图5为算例a中自齿根开始第11个接触点的面齿轮、小轮的接触应力云图，该点为三齿对啮合状态，三齿对都产生了相应的接触应力，观察齿对的接触应力云图位于节锥面附近，而相邻的齿对在齿根、齿顶处均出现了较明显的边缘接触，且接触应力偏大。

图5 面齿轮和小轮的齿面接触应力

2.3 有限元仿真与实验结果的对比

上述基于编程软件输出面齿轮传动有限元网格模型及前处理设置的方法具有较强的通用性，所以分别采用文献[24]的表3、文献[25]的表1及文献[26]的表2所示面齿轮理论齿面参数构建算例Ⅰ、算例Ⅱ、算例Ⅲ，并将算例的齿面接触应力、齿根弯曲应力最大值同文献[24-26]的仿真及实验结果进行对比，从表3看出，其误差最大均不超过7%。

表3 应力结果对比

图6(a)为文献[25]的滚检实验结果。采用文献[25]的面齿轮基本参数构建有限元网格模型，并进行TCA与LTCA分析，接触路径和印痕如图6(b)所示。由于边缘接触位置的接触印痕较宽，为在旋转投影面上清晰展示承载接触印痕，间隔一个接触点绘制一个接触椭圆。对比图6(a)、图6(b)可知算例的有限元结果与文献[25]的滚检实验结果吻合度较高。

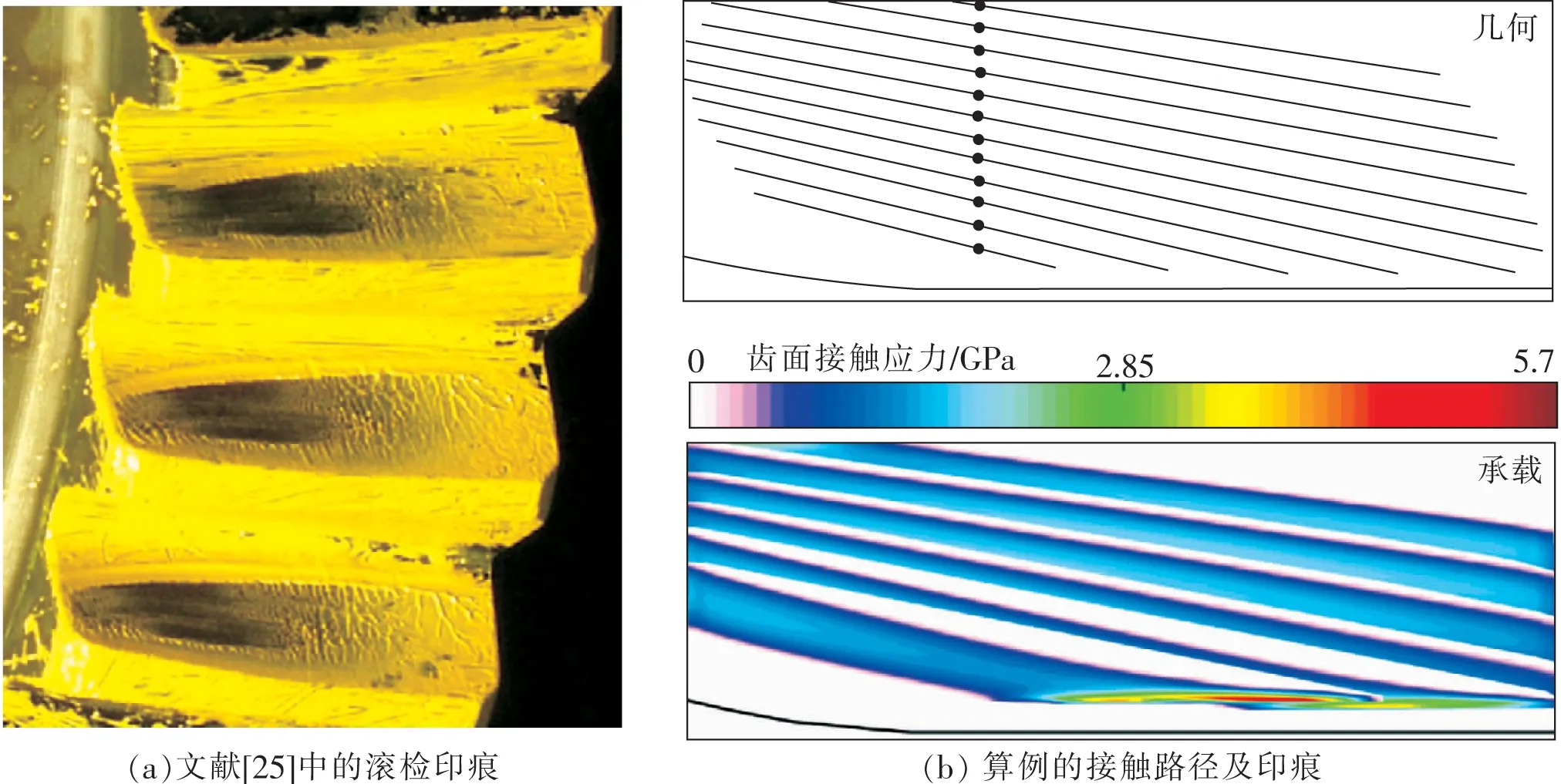
图6 面齿轮接触路径及印痕结果

由于全部算例所采用的网格密度及前处理条件均相同，所以上述应力和印痕结果间接说明了前述有限元建模方法及前处理设置的正确性。

3 计算结果及分析

3.1 对准安装的承载接触特性

图7所示为3种算例中面齿轮近似齿面的承载接触印痕，与图2相比，在齿面上TCA与LTCA的接触路径是相同的，但是在LTCA中，TCA的部分边缘接触点并未承载。尽管施加的载荷达到了1 600 N·m，3种算例中的承载接触椭圆长度都比较短，反映出了较大的齿面接触应力。

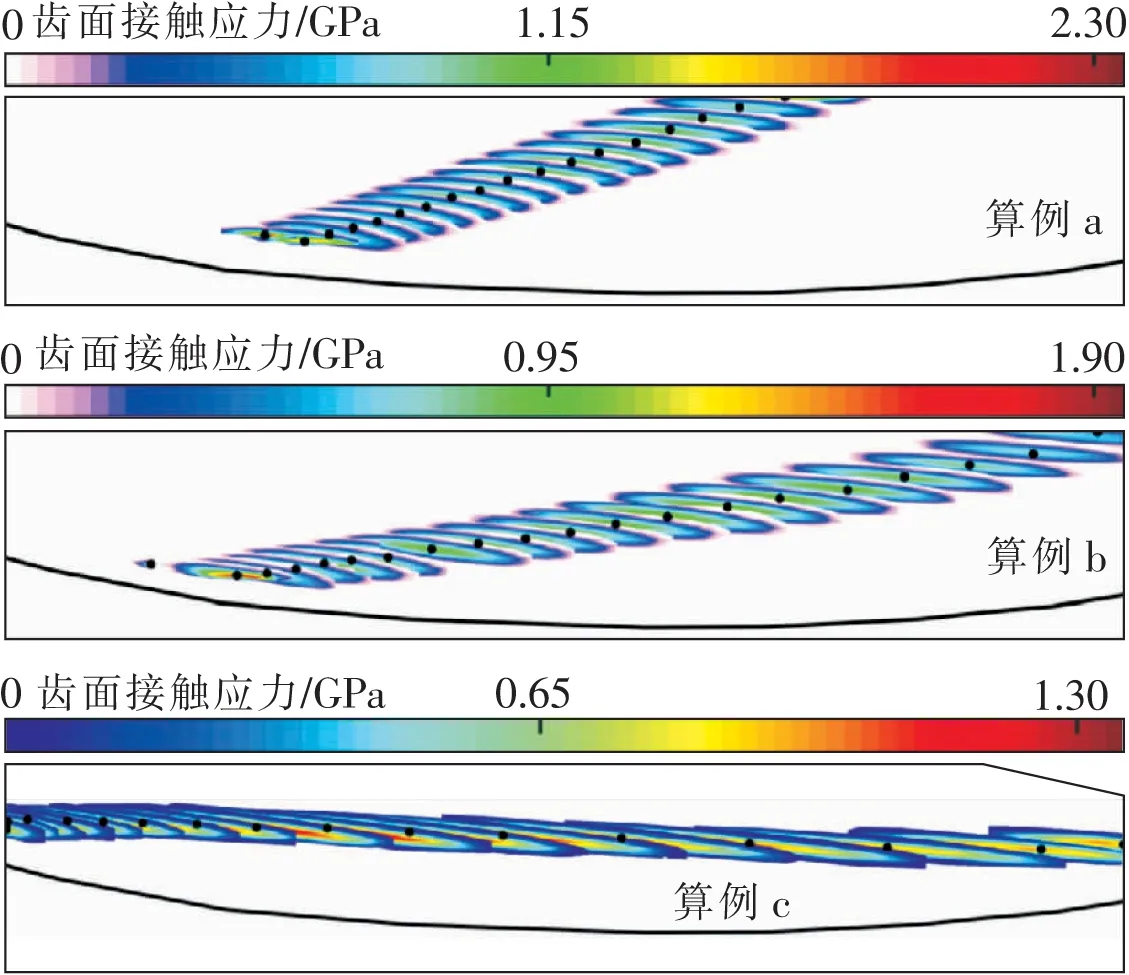
图7 承载接触印痕

图8为齿面接触应力，近似齿面和理论齿面都产生了不同程度的边缘接触，算例a，b的边缘接触应力大于理论齿面的边缘接触应力，算例c的边缘接触应力最小。3种算例的近似齿面接触应力均大于理论齿面接触应力，反映近似齿面接触强度低于理论齿面接触强度，算例b的齿面接触应力是近似齿面3种算例中最小的。

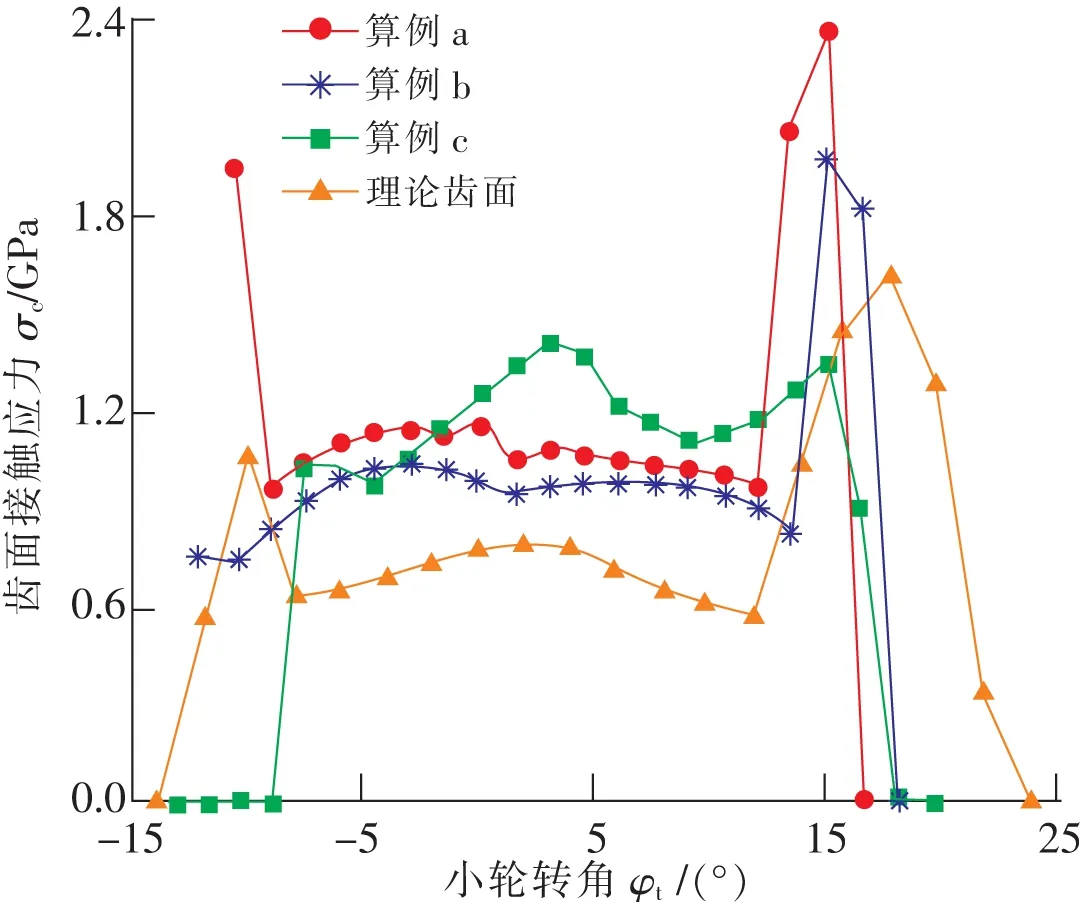
图8 齿面接触应力

图9(a)所示为近似齿面的齿根弯曲应力，算例a，c的最大齿根弯曲应力接近相等，比算例b的最大齿根弯曲应力约高23.45 MPa。3种算例中，都是当接触椭圆中心在节锥面附近时出现最大齿根弯曲应力，表明载荷主要由节锥面附近的齿面承受。理论齿面的最大齿根弯曲应力小于算例a，c的最大齿根弯曲应力，但大于算例b的最大齿根弯曲应力。

图9(b)所示为小轮齿根弯曲应力，在4种计算情况中小轮的最大齿根弯曲应力总是大于面齿轮的最大齿根弯曲应力，同样算例b中小轮的最大齿根弯曲应力在图9(b)中也是最小的。

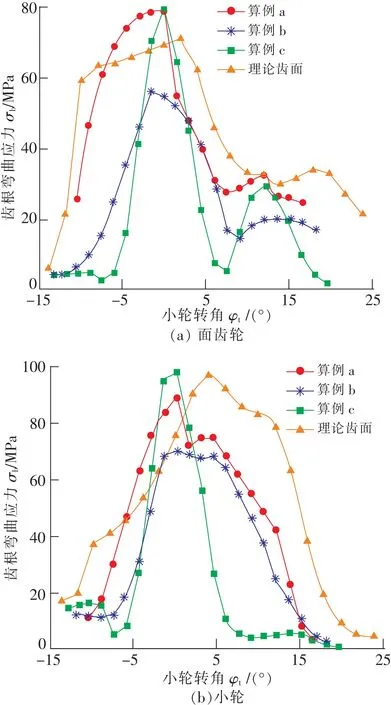
图9 面齿轮和小轮的齿根弯曲应力

图10为面齿轮近似齿面与理论齿面的承载传动误差，其波形存在一定差异，是由于预设接触路径不同，啮入啮出过程中转角不等所致。算例a中承载传动误差显示出明显的阶跃特性，这是由于三齿到两齿啮合过渡区刚好位于不承载的边缘接触点上(如图3所示)。从承载传动误差的均值上看，轮齿综合变形最小的为面齿轮理论齿面(均值为-9.85″)，其次为算例b(均值为-11.57″)。从承载传动误差的幅值上看，理论齿面的波动幅度最小(幅值为1.95″)，其次为算例b(幅值为2.21″)。因此算例b的综合啮合刚度变化、冲击与振动强度均小于算例a,c，但大于理论齿面的情况。

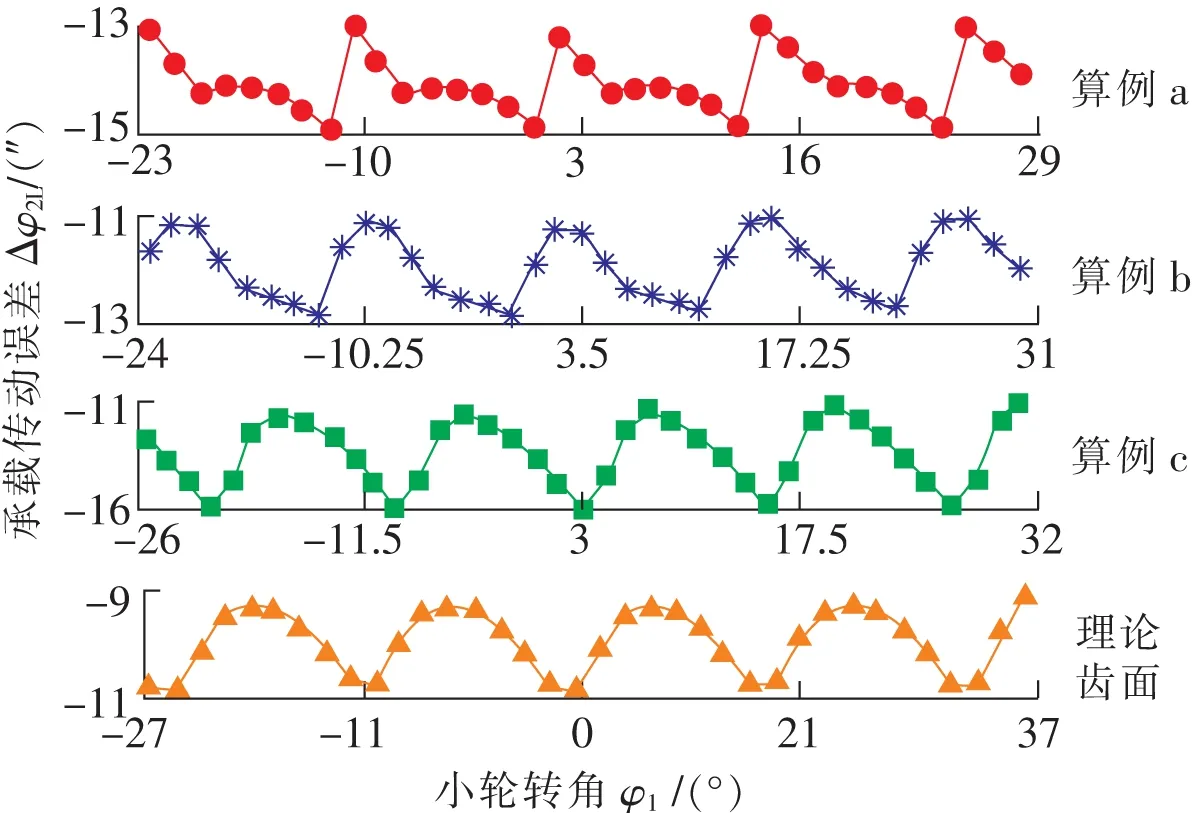
图10 承载传动误差

3.2 安装误差对承载接触特性的影响

限于篇幅，且由于在面齿轮传动中轴夹角、轴向和偏置安装误差对啮合特性的影响彼此相似，而轴夹角安装误差Δγ对啮合特性的影响较明显，算例a的预设接触路径是面齿轮传动修形齿面常见的接触路径，因此以算例a为例考察轴夹角安装误差Δγ对面齿轮近似齿面承载接触特性的影响，并与理论齿面的承载特性进行对比。

图11所示为轴夹角安装误差对齿面接触应力的影响，对于近似齿面，负值轴夹角安装误差使边缘接触应力急剧增大(从左侧纵坐标轴看)，正值轴夹角安装误差则使边缘接触应力有所减小。随轴夹角安装误差绝对值的增大近似齿面接触应力相应增大(从右侧纵坐标轴看)，而负、正值轴夹角安装误差分别使理论齿面接触应力增加和略有减小。

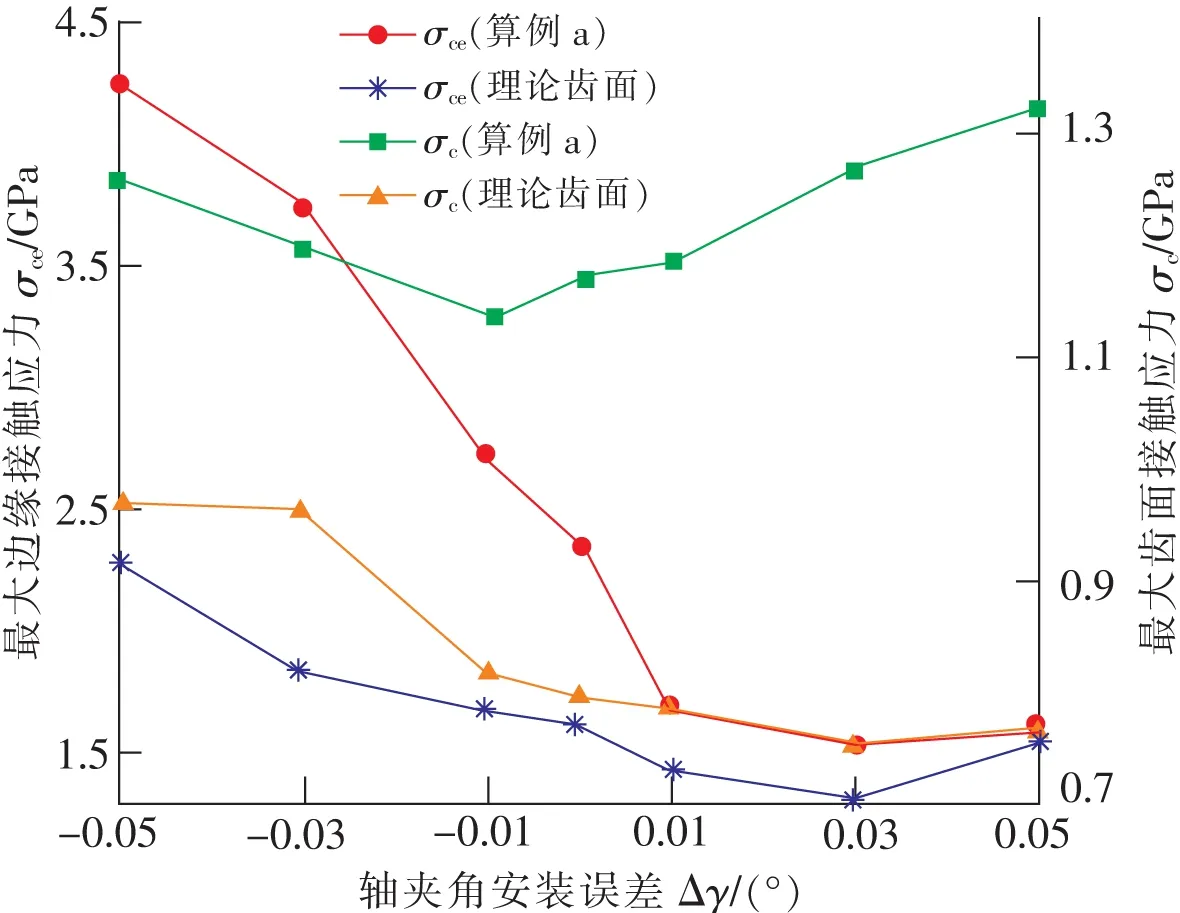
图11 安装误差对接触应力的影响

图12所示为齿根弯曲应力随轴夹角安装误差的变化情况，负值轴夹角安装误差使近似齿面齿根弯曲应力先减小后增大，正值轴夹角安装误差使近似齿面齿根弯曲应力按线性规律增大。理论齿面的齿根弯曲应力随轴夹角安装误差的变化曲线类似开口向下对称轴为Δγ=0.01°的抛物线。

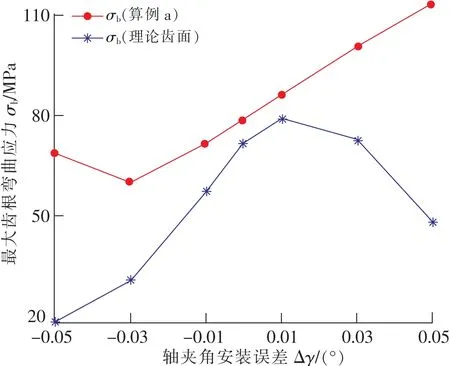
图12 安装误差对齿根弯曲应力的影响

如图13所示，在轴夹角安装误差的作用下，面齿轮近似齿面算例a的承载传动误差由阶跃波形变化为锯齿波，并且其幅值和均值都明显增大或减小，幅值由2.29″分别增加到4.77″和7.84″(从左侧纵坐标轴看)，均值由-13.86″分别减小到-25.79″和-25.93″(从右侧纵坐标轴看)，说明啮合刚度的波动幅度变大，轮齿承载啮合变形增大，刚度减小，预示冲击振动趋势增强，另一方面也说明轮齿承载啮合接触面积减小。

图13 安装误差对承载传动误差的影响

如图13所示，在轴夹角安装误差的作用下，面齿轮理论齿面的承载传动误差幅值均有所增加，均值有增有减，总体上它们变化的幅度均小于算例a。

4 结 论

1)提出了一种基于编程软件输出面齿轮传动有限元网格模型及前处理设置的方法，将inp文件批处理导入有限元软件ABAQUS中求解承载接触问题，提高了齿面重构和安装精度，能够充分考虑齿面修形、安装误差对面齿轮承载接触特性的影响。

2)对3组不同面齿轮基本参数的理论齿面进行有限元仿真分析，并将分析结果与文献中的仿真及实验结果进行对比，间接证明了文中所述建模方法及前处理设置的正确性。

3)在直刃刀具加工的面齿轮近似齿面建模和TCA的基础上，计算了由3种不同预设接触路径综合出的近似齿面的承载接触问题，几何接触路径与承载接触路径相同，若不考虑边缘接触，从齿面接触应力、齿根弯曲应力、承载传动误差等方面考虑，按齿面对角线预设接触路径(算例b)综合刀具运动规律进而加工面齿轮近似齿面，最可取。

4)与面齿轮理论齿面相比，近似齿面的接触强度低，合理选取预设接触路径可使得近似齿面的齿根弯曲强度高于理论齿面。

5)安装误差对面齿轮近似齿面承载接触特性的影响高于理论齿面，并导致接触强度、弯曲强度降低，加剧冲击与振动。