基于实测点坐标的圆柱齿轮齿面偏差评定方法
李伟东 李文涛 杨易凯 曹雪梅 念朝晖
(1 河南科技大学 机电工程学院, 河南 洛阳 471003)
(2 河南科技大学 学生处, 河南 洛阳 471003)
(3 河南科技大学 国际教育学院, 河南 洛阳 471003)
0 引言
为了提高齿轮啮合性能,通常采用对渐开螺旋面拓扑修形的方法,即沿齿廓和齿宽进行修正[1],这需要将全齿面拓扑偏差信息用于齿面精密加工的数字化控制。目前,实现齿轮精度全面、高精度、低成本的测量仍然是研究的热点。石照耀等[2]提出圆柱齿轮齿面三维误差表征可充分挖掘齿轮误差信息中包含的物理和工程意义参数;基于啮合坐标系表征齿面误差,通过Legendre 多项式分解了齿面误差。林虎等[3]提出了一种基于正交距离回归齿面的误差计算方法,研究了齿面特征线误差的评定算法和拓扑齿形误差的计算与分解。曹雪梅等[4]1799-1780提出了一种基于三坐标测量的弧齿锥齿轮的齿面检测方法,为齿面质量控制数字化提供了条件。Pei 等[5]提出了高精度齿廓径向跳动测量算法。林家春等[6]利用激光跟踪仪采集齿面数据点,获得了大型齿轮齿廓偏差。魏建杰等[7]对ISO 1328-1:2013的齿廓偏差定义及评定方法进行了计算和分析。Koulin 等[8]利用粗糙度测量仪检测表面特征,建立了粗糙度与齿廓偏差相关联的数学模型,并进行了试验验证。Lin 等[9-10]利用拟合算法实现渐开线圆柱齿轮齿廓测量数据与理论齿廓模型拟合,得到了齿廓偏差曲线。
随着齿面拓扑修形技术的广泛使用,综合评价拓扑修形齿面是加工参数反调修正及齿轮副啮合性能评价的重要依据。齿轮检测中心仅提供了齿廓偏差和螺旋线偏差,无法全面评价齿面拓扑结构,难以满足圆柱修形齿轮齿面加工反调修正的目的。本文中根据圆柱齿轮齿面实测点坐标,通过角向定位,建立实测点与理论渐开螺旋面齿面点的一一映射关系,计算了齿面三维拓扑偏差;在此基础上降维处理,得到二维偏差曲线——齿廓偏差、螺旋线偏差;采用最小二乘法建立了齿廓偏差和螺旋线偏差的评定方法。通过提炼齿面三维测量数据,为齿面精密加工数字化控制和啮合性能评估提供依据。
1 构建实测齿面的齿面拓扑偏差
1.1 建立理论渐开线螺旋面方程
理论斜齿圆柱齿轮齿面为标准渐开线螺旋面,其齿面方程为
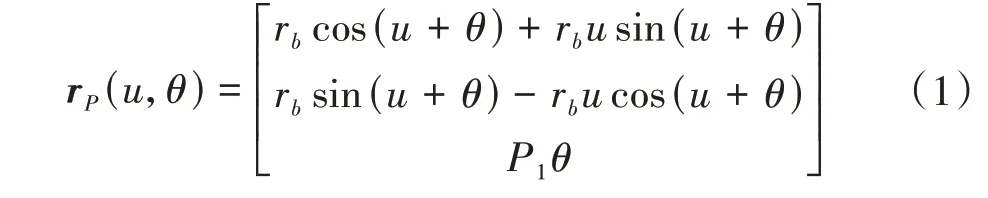
式中,u、θ均为齿面参数;rb为基圆半径;P1为螺旋参数,有

式中,mn为法向模数;z为齿数;β为齿轮螺旋角,左旋为正,右旋为负。
1.2 确定与实测点对应的理论齿面点
图1所示为齿面旋转投影面,横坐标轴H为齿轮的回转轴,纵坐标轴R轴为旋转投影轴。为了避让倒角区和齿根过渡曲面,应设定齿面检测范围,m为齿宽方向检测点数,n为齿高方向检测点数。设实测齿面点为p′ij(x′ij,y′ij,z′ij)(其中,i=1,2,…,m;j=1,2,…,n)。根据实测点坐标确定相应的理论齿面点,理论齿面点为Pij(xij,yij,zij)。
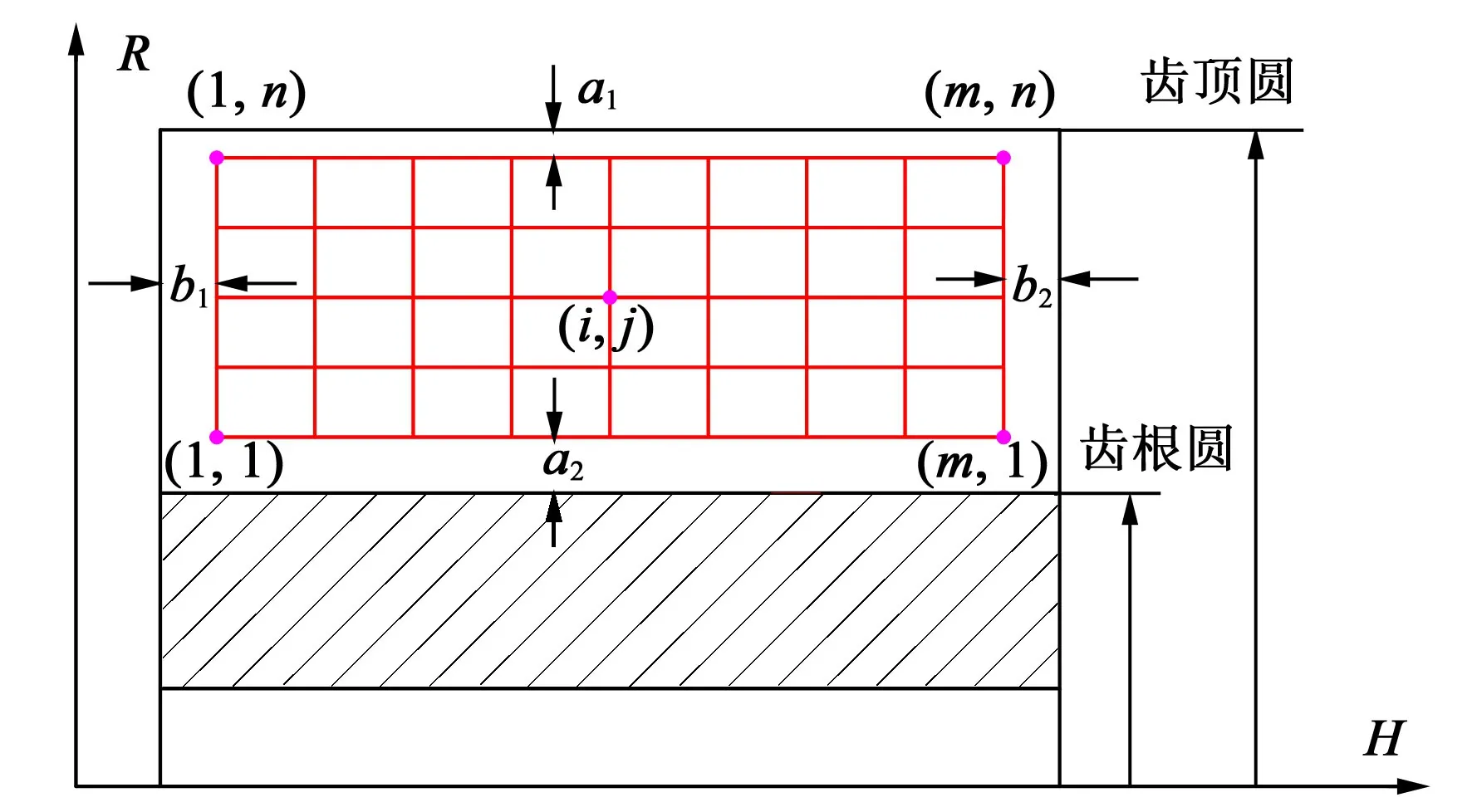
图1 齿面网格规划Fig.1 Tooth surface mesh planning
将齿面所有实测点投影到旋转投影面上,其坐标值为

其中,i= 1,2,…,m;j= 1,2,…,n。
实测点与对应理论齿面点在旋转投影面的位置重合,在二维投影平面的位置关系为
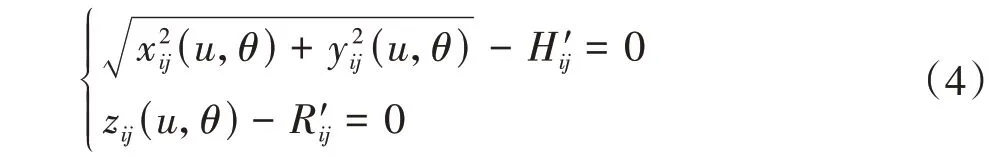
其中,i= 1,2,…,m;j= 1,2,…,n。
求解该二维非线性方程组,即可求出理论齿面点的参数(u,θ),进而确定与实测点对应的理论齿面点Pij坐标(xij,yij,zij)。
1.3 实测齿面的角向定位
理论齿面和实测齿面在齿轮不同的角向位置,因此,需进行角向定位[4]1800-1801,即角向基准重合。实际齿面转动ψ角度后,角向定位基准点(x′m,y′m,z′m)应与理论齿面重合,完成实测齿面的角向定位,即
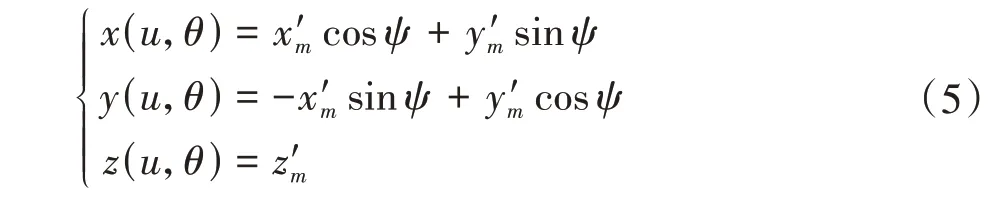
求解三维非线性方程组(5),得到实测齿面与理论齿面在基准点重合时的θ、u、ψ;再将所有测点全部绕z轴旋转ψ角,即可完成角向定位,即
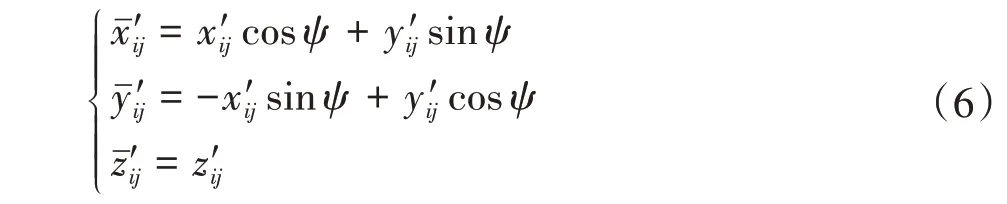
其中,i= 1,2,…,m;j= 1,2,…,n。
1.4 实测齿面与理论齿面拓扑偏差
齿面拓扑偏差定义为:沿理论齿面给定测点法线方向,实际齿面测点与理论齿面的偏离距离。实测点的齿面误差为
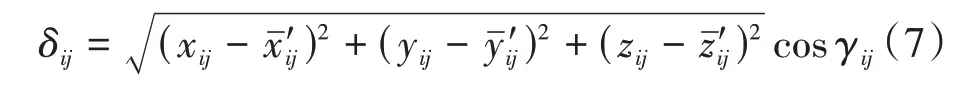
式中,γij为实际齿面测点到理论齿面测点的连线与理论齿面测点法线的夹角。其中,i= 1,2,…,m;j= 1,2,…,n。
图2所示为齿面拓扑偏差图。图2中,R为齿高方向,H为齿宽方向。网格点对应的偏差为测点偏差值。

图2 齿面拓扑偏差图Fig.2 Tooth surface topological deviation diagram
2 实测齿面偏差评定
2.1 实测齿面齿廓偏差评定
齿廓偏差定义为:在端截面上,齿廓工作部分内,包容实际齿廓且距离为最小的两条设计齿廓间的法向距离。根据最小二乘法确定齿廓的方法为:寻找一条最短直线,使各个采样点偏差值相对于该理想直线的偏差的平方和最小。所得到的极值之差作为评定的误差值,所得到的直线即为平均齿廓迹线[11]。齿廓偏差可分为齿廓总偏差Fα、齿廓形状偏差ffα和齿廓倾斜偏差fHα。
根据构建的齿面拓扑偏差图,做H轴的切片,得到不同齿宽位置的齿轮端截面齿廓偏差曲线图,如图3 所示。图3 中,δj轴为实测点的齿廓偏差值;tj轴为测量点位置。平均齿廓迹线可采用最小二乘法确定。
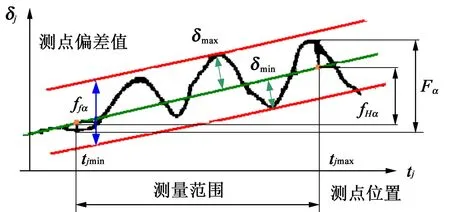
图3 齿廓偏差示意图Fig.3 Schematic diagram of tooth profile deviation
设平均齿廓迹线方程为
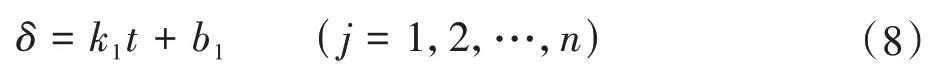
则各个测点到平均齿廓迹线的偏差为

偏差的平方和为

根据最小二乘法原理,偏差值的平方和最小。为使Q1值最小,有
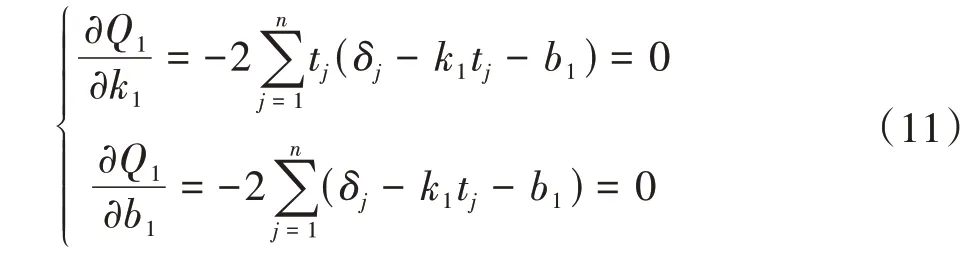
求解方程得
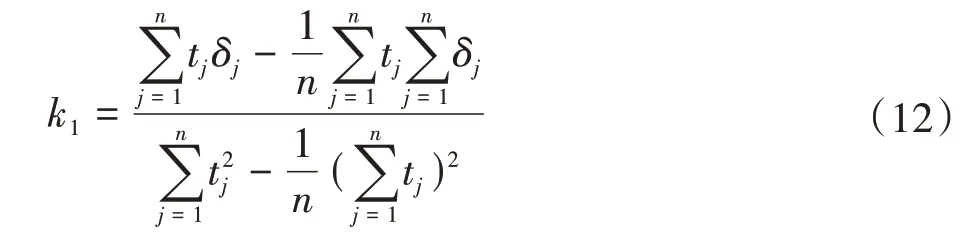
齿廓形状偏差ffα、齿廓倾斜偏差fHα和齿廓总偏差Fα分别为
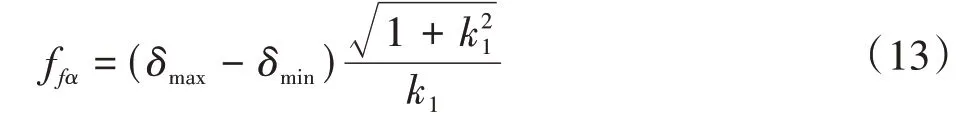
式中,δmax、δmin分别为实测点到平均齿廓迹线的最大、最小距离。
式中,tjmax、tjmin分别为实测点起始与截至位置坐标。

式中,δjmax、δjmin分别为实测点最大、最小偏差。
2.2 实测齿面螺旋线偏差评定
螺旋线偏差定义为:在端面基圆切线方向上测得的实际螺旋线偏离设计螺旋线的量。螺旋线偏差可分为螺旋线总偏差Fβ、螺旋线形状偏差ffβ和螺旋线倾斜偏差fHβ,其中,螺旋线倾斜偏差fHβ反映的是斜齿圆柱齿轮螺旋角偏差。
根据齿面拓扑偏差图,做R轴的切片,得到不同齿高位置的螺旋线偏差图。图4所示为螺旋线偏差示意图。
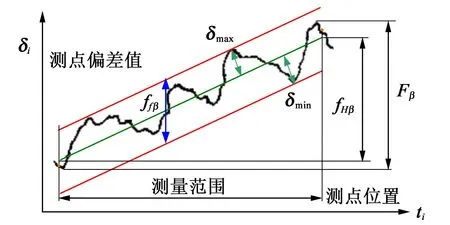
图4 螺旋线偏差示意图Fig.4 Schematic diagram of helix deviation
同理,根据最小二乘法原理,确定平均螺旋线迹线,计算测点到平均螺旋线迹线的最大、最小距离分别为δmax、δmin,进而确定螺旋线总偏差Fβ、螺旋线形状偏差ffβ和螺旋线倾斜偏差fHβ。
3 算例分析
3.1 齿轮参数
检测一个圆柱齿轮,齿轮参数如表1所示。根据实测齿面点坐标,计算三维齿面拓扑偏差及齿廓偏差和螺旋线偏差;在Gleason 650GMS 测量中心检测齿轮精度(图5),并对齿轮偏差结果进行分析对比。

表1 齿轮参数Tab.1 Gear parameters

图5 Gleason 650GMS检测Fig.5 Gleason 650GMS detection
3.2 齿面偏差分析
齿宽方向检测点数为5个,齿廓方向检测点数为9 个,根据测点坐标值,计算齿面偏差。图6 所示为实测齿面拓扑偏差图,从图6中可以看出,齿面偏差主要是压力角偏差;齿顶部螺旋线偏差较大。

图6 实测齿面拓扑偏差图Fig.6 Topological deviation diagram of measured tooth surface
3.3 齿廓偏差评定
沿齿宽方向对齿面拓扑偏差图切片,得到齿廓偏差图。图7所示为齿宽位置20.529 mm的齿廓偏差曲线,表2 所示为计算得到的齿廓倾斜偏差fHα、齿廓总偏差Fα和齿廓形状偏差ffα。
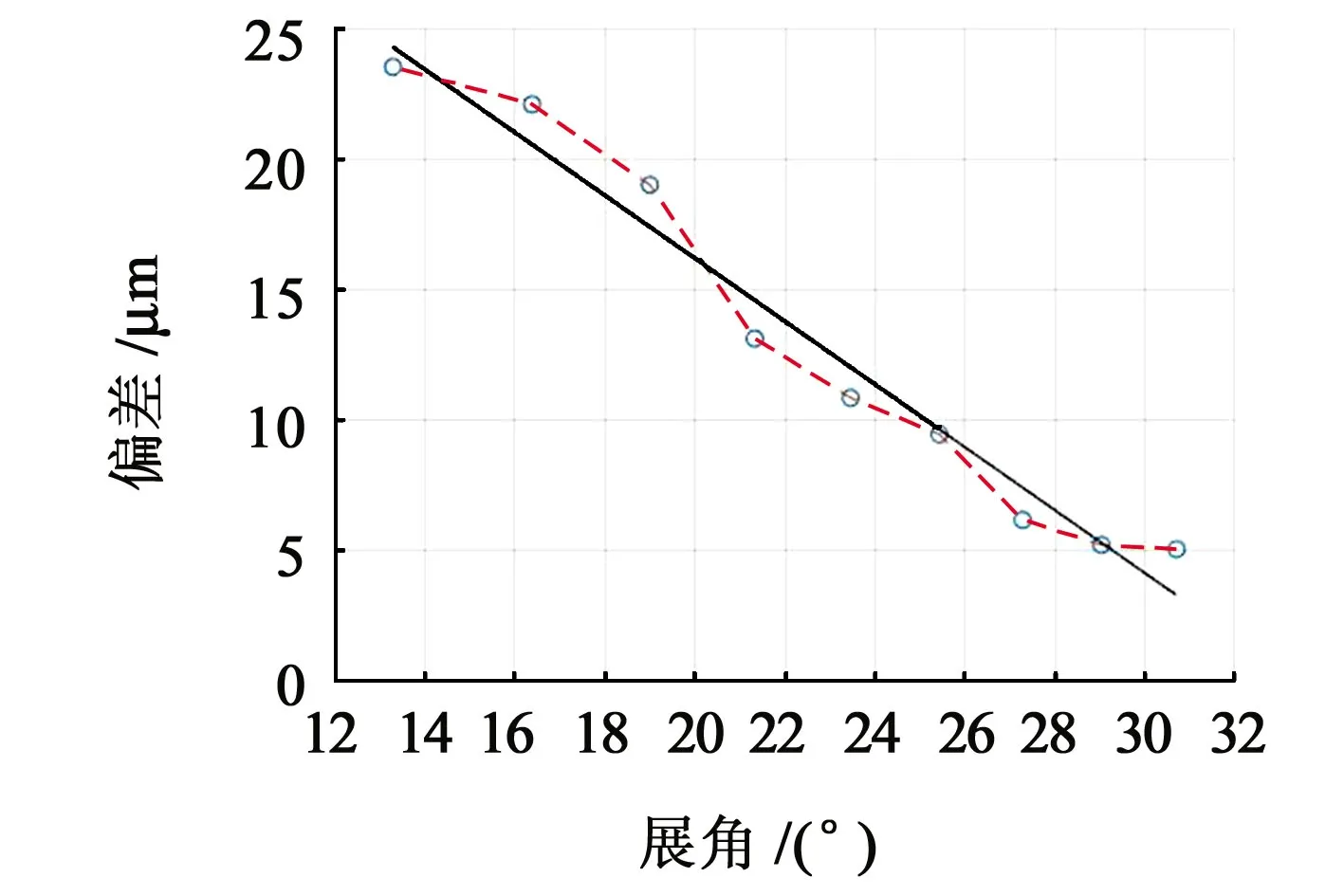
图7 齿廓偏差图Fig.7 Tooth profile deviation diagram

表2 齿廓偏差计算结果Tab.2 Tooth profile deviation calculation results
图8 所示为Gleason 650GMS 检测的齿廓偏差图及检测报告单。
对比表2 和图8 中可知,本文中方法计算的齿廓倾斜偏差fHα为-18.4 μm,Gleason 650GMS 检测结果为-20.4 μm,差值为2.0 μm;本文中方法计算的齿廓总偏差Fα均值为19.9 μm,Gleason 650GMS 检测结果为19.5 μm,差值为0.4 μm;本文中方法计算的齿廓形状偏差ffα均值为3.3 μm,Gleason 650GMS检测结果为5.5 μm,差值为2.2 μm。
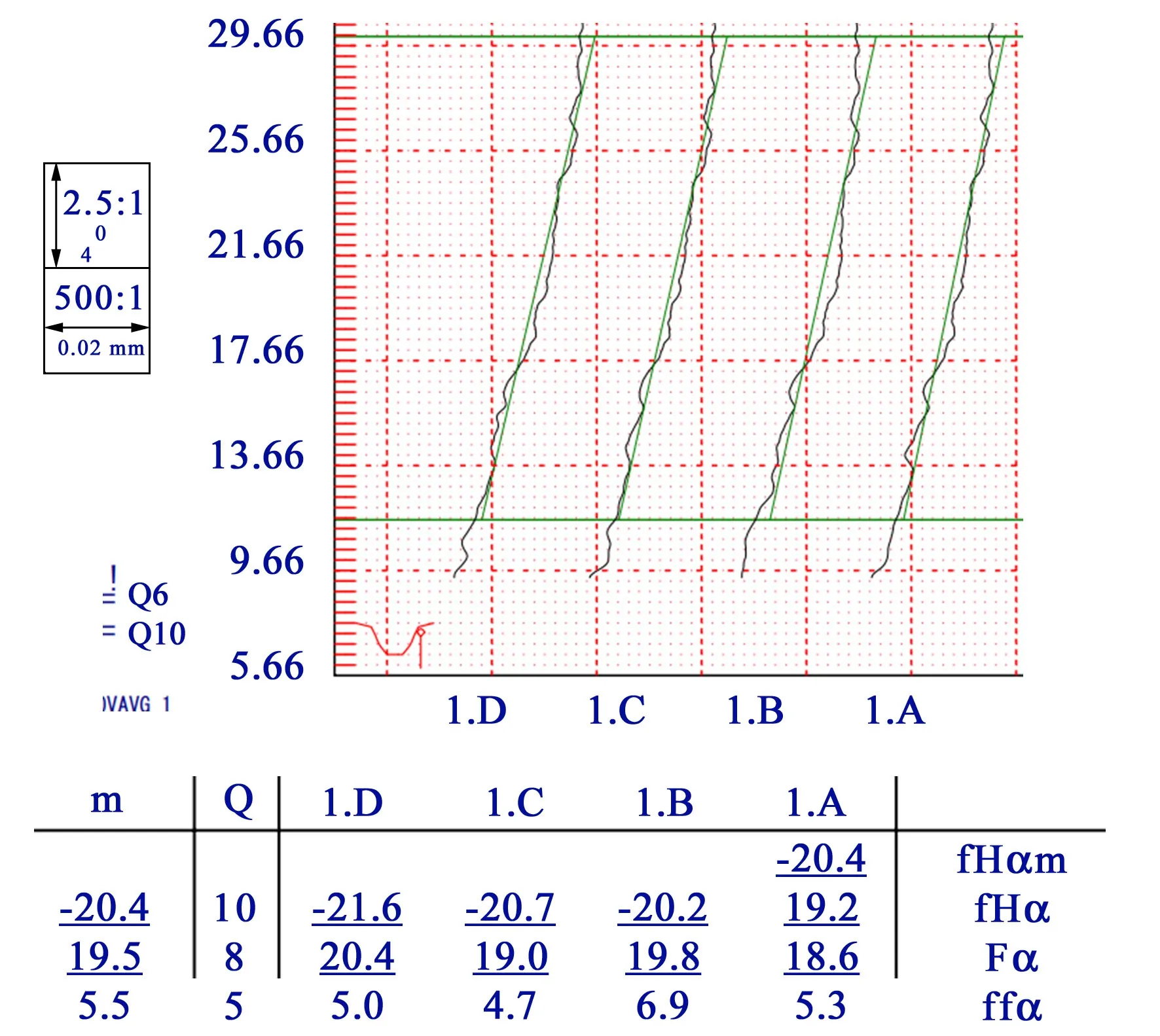
图8 Gleason 650GMS齿廓偏差检测报告Fig.8 Gleason 650GMS tooth profile error detection report
3.4 螺旋线偏差评定
沿齿高方向对齿面拓扑偏差图切片,得到螺旋线偏差图。图9 所示为展角23.46°的螺旋线偏差图,表3 所示为计算得到的螺旋线倾斜偏差fHβ、螺旋线总偏差Fβ和螺旋线形状偏差ffβ。
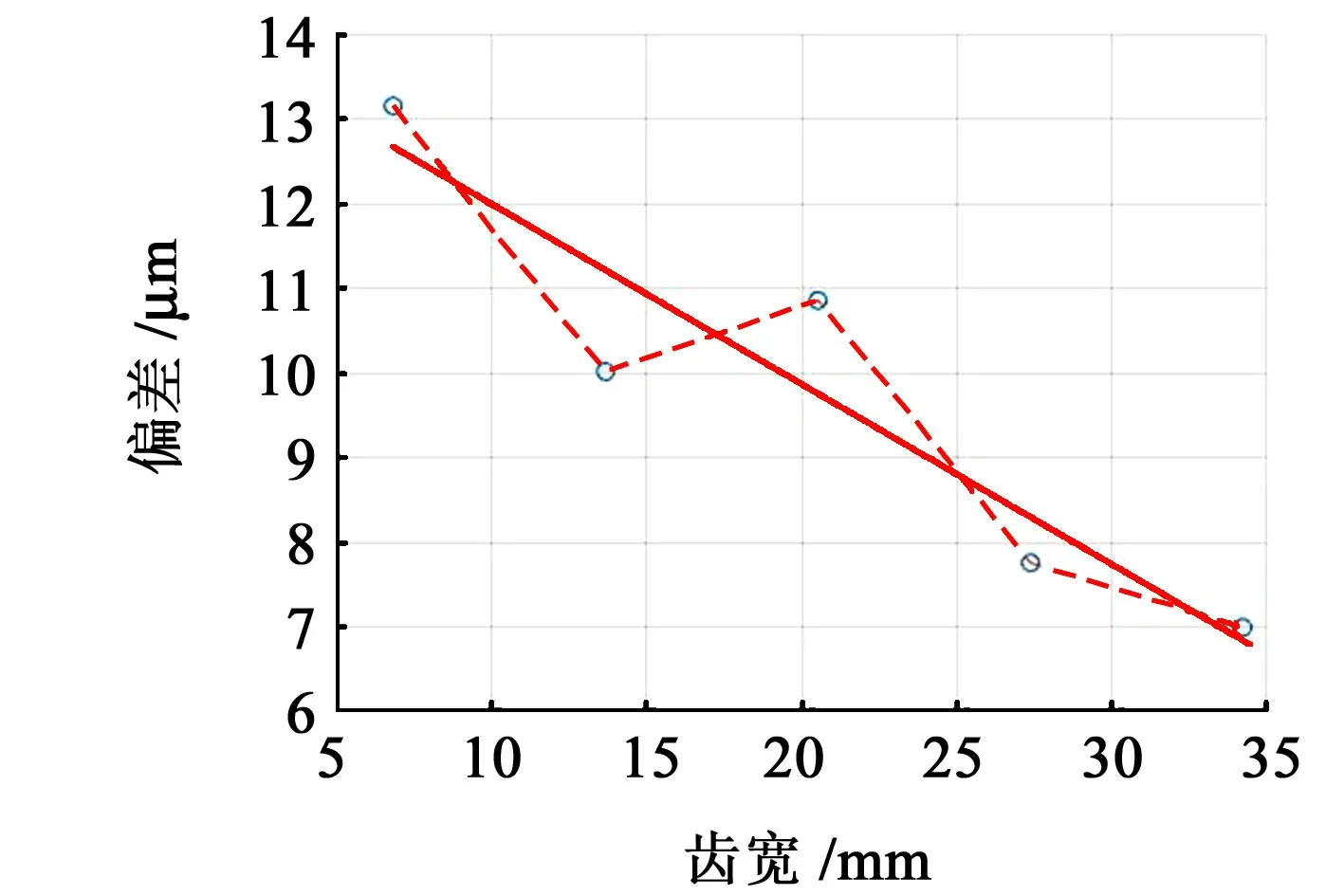
图9 螺旋线偏差图Fig.9 Helix deviation

表3 螺旋线偏差计算结果Tab.3 Helix deviation calculation results
图10 所示为Gleason 650GMS 检测的螺旋线偏差图及检测报告单。
对比表3 和图10 中可知,本文中方法计算的螺旋线倾斜偏差fHβ均值为-6.1 μm,Gleason 650GMS检测结果为-6.4 μm,差值为0.3 μm;本文中方法计算的螺旋线总偏差Fβ均值为6.4 μm,Gleason 650GMS检测结果为7.1 μm,差值为0.7 μm;本文中方法计算 的 螺 旋 线 形 状 偏 差ffβ均 值 为2.3 μm,Gleason 650GMS检测结果为3.2 μm,差值为0.9 μm。
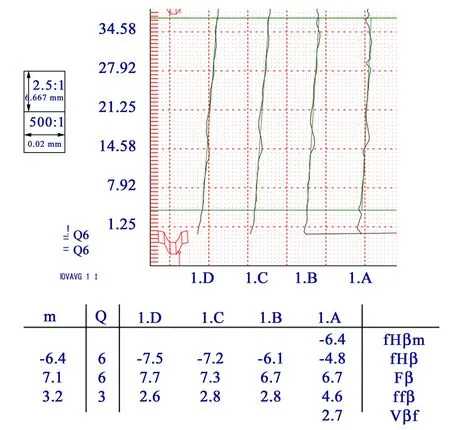
图10 Gleason 650GMS螺旋线偏差检测报告Fig.10 Gleason 650GMS spiral deviation detection report
根据实测点数据,计算齿廓偏差和螺旋线偏差,计算结果与Gleason 650GMS 检测报告基本一致。本文中仅对1 个齿面沿齿宽中点和展角位置计算了齿廓偏差、螺旋线偏差。Gleason 650GMS 检测中心测量检测了4 个齿面,计算平均偏差,结果也将更加精确。
4 结论
基于圆柱齿轮实测齿面点坐标,构建齿面三维拓扑偏差图,直观地反映了全齿面偏差,为全齿面数字化控制提供了依据;基于齿面三维拓扑偏差图,沿齿宽和齿高方向切片,得到不同位置的齿廓偏差曲线和螺旋线偏差曲线,给出齿廓偏差和螺旋线偏差计算方法。由本文中方法检测结果与Gleason 650GMS齿轮检测中心的检测报告对比可知,计算精度与Gleason 650GMS 报告基本一致。本文中方法可为齿面精密数字化控制提供依据。
——以徐州高层小区为例

