借助函数对称性,巧解数学综合题
■孙艳艳
函数的对称性是函数基本性质中最为特殊的一个性质,在历年高考命题中,函数的对称性常与函数的其他性质综合交汇,成为数学分析、数学应用与数学研究的一大有力工具。
一、函数对称性的一些重要“二级结论”
性质1:函数y=f(x+a)是偶函数⇔函数y=f(x)的图像关于直线x=a对称⇔等式f(a+x)=f(a-x)成立。
性质2:函数y=f(x+a)是奇函数⇔函数y=f(x)的图像关于点(a,0)中心对称⇔等式f(a+x)=-f(a-x)成立。
推论1:等式f(x)+f(2a-x)=0成立⇔函数y=f(x)的图像关于点(a,0)中心对称⇔函数y=f(x+a)是奇函数。
推论2:函数y=f(x+a)-b是奇函数⇔函数y=f(x)的图像关于点(a,b)中心对称⇔等式f(a+x)+f(a-x)=2b成立。
性质3:函数y=f(a+x)与y=f(ax)的图像关于y轴对称,函数y=f(a+x)与y=-f(a-x)的图像关于坐标原点对称。
二、函数对称性的综合应用
1.函数值的求解
例1 设函数f(x)的定义域为R,f(x+1)为奇函数,f(x+2)为偶函数,当x∈[1,2]时,f(x)=ax2+b。若f(0)+f(3)=3,则的值是( )。
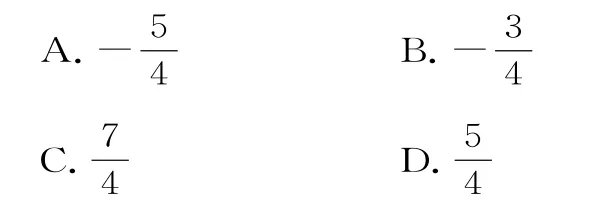
分析:结合抽象函数的奇偶性和函数对称性的性质,构建函数关系式,确定函数的周期,利用赋值求出函数的解析式,即得函数的值。
解:由f(x+1)为奇函数,结合性质2得函数f(x)的图像关于点(1,0)对称,则f(1)=0,且f(x+1)=-f(-x+1)。 ①
由f(x+2)为偶函数,结合性质1 得函数f(x)的图像关于直线x=2 对称,则f(x+2)=f(-x+2)。 ②

熟练掌握一些函数对称性及其对应的关系式,可以较快构建一些合适的关系式,为问题的有效解决奠定基础。
2.代数式的求解
例2 已知函数f(x)=(2x2-4x+3)·(ex-1-e1-x)-2x+1在区间[0,2]上的最大值为M,最小值为m,则M+m=。
分析:构造函数g(x),结合关系式的结构特征,得到g(x)+g(2-x)=0,确定函数g(x)的中心对称,利用对称性的基本性质即可求值。

由函数对称性的基本性质,可知M+m=-1×2=-2。
抓住函数关系式的变形与应用,构建不同函数关系式之间的联系,为进一步利用函数的对称性质提供条件。
3.不等式的求解
例3 已知f(x-1)是定义在R 上的奇函数,f(1)=0,且f(x)在[-1,0)上单调递增,在[0,+ ∞)上单调递减,则不等式f(2x-3)<0的解集为( )。
A.(1,2)
B.(-∞,1)
C.(2,+∞)
D.(-∞,1)∪(2,+∞)
分析:利用函数的对称性与单调性,确定函数的单调区间,通过自变量取值的分类讨论,得到不等式的解集。
解:由f(x-1)是定义在R 上的奇函数,结合性质2得f(x-1)=-f(-x-1),即函数f(x)的图像关于点(-1,0)对称。
当x=-2 时,代入上式得f(-3)=-f(1)=0,当x=0时,代入上式得f(-1)=-f(-1),即f(-1)=0。由f(x)在[-1,0)上单调递增,在[0,+∞)上单调递减,利用奇函数f(x)关于(-1,0)对称知f(x)在(-∞,-2)上单调递减,在(-2,0)上单调递增,在(0,+∞)上单调递减。
对于不等式f(2x-3)<0,当2x-3<-2时,2x-3>-3,解得x<0;当-2≤2x-3≤0时,2x-3<-1,解得0≤x<1;当2x-3>0时,2x-3>1,解得x>2。
综上可得,不等式f(2x-3)<0 的解集为(-∞,1)∪(2,+∞)。应选D。
解题时,注意分类讨论的巧妙应用,以及函数单调性的逆向应用。
4.综合应用问题
例4 已知函数f(x)的定义域为R,且f(x+2)为偶函数,f(2x+1)为奇函数,则下列选项中的值一定为0的是( )。

C.f(2) D.f(4)
分析:结合题设条件,确定函数的周期性,利用奇函数的性质确定对应的特殊值,为问题的判断提供有力根据。
解:由函数f(x+2)为偶函数,结合性质1得f(2+x)=f(2-x),则f(x+3)=f(1-x)。由函数f(2x+1)为奇函数,结合性质2 得f(1-2x)=-f(2x+1),所 以f(1-x)=-f(x+1),所以f(x+3)=-f(x+1),则f(x+1)=-f(x-1),所以f(x+3)=f(x-1),即f(x)=f(x+4),故函数f(x)是以4为周期的周期函数。因为f(2x+1)为奇函数,所以f(1)=0,所以f(-1)=f(-1+4)=f(3)=f(2+1)=-f(1)=0,B 正确。由f(2+x)=f(2-x),令x=2,可得f(4)=f(0),f(0)的值无法确定,D 错误。由f(x+2)=-f(x),f(0)的值无法确定,可知f(2)的值无法确定,C错误。同理,的值也无法确定,A 错误。应选B。
这里综合函数的奇偶性、对称性与周期性,结合几个不同函数值的设置,巧妙得到函数值为0 的一个选项。

