例说分类讨论思想在解题中的应用
■洪高翔
把所研究的问题根据题目的特点和要求,分成若干类,转化成若干个小问题来解决,这种按不同情况分类,再逐一研究解决问题的数学思想,称为分类讨论思想。下面就分类讨论思想在解题中的应用,进行举例分析,供大家学习与提高。
一、对函数自变量的分类讨论
例1 已知函数f(x)对任意x∈R,都有,当x∈[0,2]时,f(x)=-x2+2x,则函数f(x)在[-2,6]上的值域为( )。
C.[-2,0] D.[-2,4]

综上可得,函数f(x)在[-2,6]上的值域为[-2,4]。应选D。
评注:解决分段函数的策略就是“分段函数,分段解决”。
二、对指数函数、对数函数的底数分类讨论
例2 设a>0,且a≠1,函数y=a2x+2ax-1在[-1,1]上的最大值是14,则实数a的值为____。
解:令t=ax(a>0,且a≠1),则原函数可化为f(t)=t2+2t-1=(t+1)2-2(t>0)。

评注:指数函数y=ax与对数函数y=logax的底数a满足的条件是a>0且a≠1。
三、对二次函数的对称轴分类讨论
例3 若函数f(x)=x2-2x-2ax+2,x∈[1,2],则f(x)的最小值为_____。
解:函数f(x)=x2-2x-2ax+2的对称轴方程为x=a+1。
当a+1≤1,即a≤0 时,f(1)=1-2a为最小值;当1
综上可得,函数f(x)的最小值为
评注:二次函数y=ax2+bx+c(a≠0)的对称轴方程为(即顶点的横坐标)。本题需要考虑在区间[1,2]上,或在区间[1,2]外的情况。
四、对函数的值域分类讨论
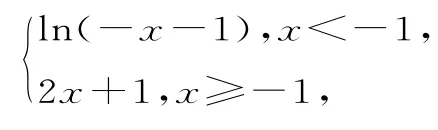
例 4 已 知 函 数f(x) =若函数g(x)=f[f(x)]-a有三个不同的零点,则实数a的取值范围是_____。
解:设t=f(x),令f[f(x)]-a=0,则a=f(t)。在同一坐标系内,作出y=a,y=f(t)的图像(如图1)。

图1
由图可知,当a≥-1 时,y=a与y=f(t)的图像有两个交点,设交点的横坐标为t1,t2(不妨设t2>t1),则t1<-1,t2≥-1。
当t1<-1时,t1=f(x),即t1=f(t)有一解;当t2≥-1时,t2=f(x),即t2=f(t)有两解。
综上可得,当a≥-1,即a∈[-1,+∞)时,函数g(x)=f[f(x)]-a有三个不同的零点。
评注:题中t=f(x)的意义是函数f(x)的值域。在复合函数中,内层函数的值域是外层函数的定义域。
五、对参数的分类讨论
例5 (1)已知角α的终边过点P(-3a,4a)(a≠0),则2sinα+cosα的值为_____。

评注:(1)中的参数a是实数,a的取值范围决定角α的终边所在的象限;(2)中的参数k是整数,需要分奇数与偶数讨论。


