打造“模特”函数,巧解抽象函数
■赵荣涛
巧妙构造满足抽象函数的结构特征的具体函数,是解决抽象函数问题的一种巧技妙法。借助抽象函数的基本结构特征,选取与之相吻合的“模特”函数(基本上以高中阶段所学的基本初等函数为主,如一次函数、指数函数、对数函数,以及三角函数等),结合系数的配凑处理,实现抽象函数问题的圆满解决。
一、一次函数模型
例1 定义在R 上的函数f(x)满足f(x+y)=f(x)+f(y),且当x>0 时,有f(x)<0成立,则不等式f(5-x2)+f(3x-x2)<0的解集为( )。
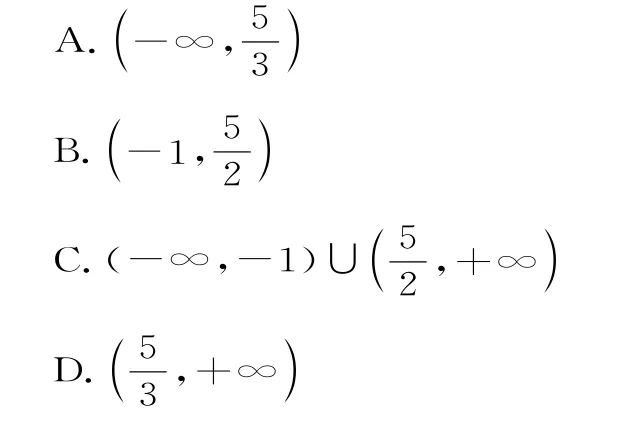
分析:由f(x+y)=f(x)+f(y),类比并联想到一次函数模型,考虑“模特”函数为正比例函数,利用条件确定正比例函数中k的取值,代入对应的不等式进行求解。
解:由f(x+y)=f(x)+f(y),构建特殊函数模型f(x)=kx,k≠0。
由条件知当x>0 时,f(x)<0,取k=-1,则f(x)=-x,所以不等式f(5-x2)+f(3x-x2)<0 可化为-(5-x2)-(3xx2)<0,整理得2x2-3x-5<0,解得-1<故不等式f(5-x2)+f(3x-x2)<0的解集为。应选B。
一次函数模型f(x)=kx+b(k≠0),满足f(x+y)=f(x)+f(y)。解题时,抓住函数的单调性、函数值的取值情况,确定系数k的值,为问题的进一步求解奠定基础。
二、指数函数模型
例2 已知定义域为R 的函数f(x)满足:①对任意x,y∈R,有f(x+y)=f(x)f(y)恒成立;②若x≠y,则f(x)≠f(y)。以下选项表述不正确的是( )。
A.f(x)在R 上是严格增函数
B.若f(3)=10,则f(6)=100
C.若f(6)=100,则f(-3)=
D.函数F(x)=f(x)+f(-x)的最小值为2
分析:由f(x+y)=f(x)f(y),类比并联想到指数函数模型,考虑“模特”函数为指数函数,结合指数函数的图像与性质进行分析与判断。
解:由f(x+y)=f(x)f(y),构建特殊函数模型f(x)=ax,a>0且a≠1。
当0 指数函数模型f(x)=ax,a>0 且a≠1,满 足f(x+y)=f(x)f(y)。解题时,先利用函数的单调性、模型函数的取值,确定函数的值,再结合基本不等式进行分析与处理。 例3 (多选题)定义在(0,+∞)上的函数f(x)满足如下条件:①f(xy)=xf(y)+yf(x);②当x>1 时,f(x)>0。下列结论中正确的是( )。 A.f(1)=0 B.f(xy)=f(x)f(y) C.f(x)在(1,+∞)上单调递增 分析:由f(xy)=f(x)+f(y),类比并联想到对数函数模型,考虑“模特”函数为对数函数,再结合题意进行分析与处理。 对数函数模型f(x)=logax,a>0 且a≠1,满 足f(xy)=f(x)+f(y)。需要注意的是,在构建函数模型时,经常要对相应的关系式进行恒等变形转化为熟悉的关系式,这样方便联系与类比对应的特殊函数模型。 例4 (多选题)函数f(x)为定义在R上的偶函数,f(0)=1,且f(x-1)+f(x+1)=f(x)。下列结论中正确的是( )。 分析:利用抽象函数的结构特征,类比联想三角函数,结合偶函数的基本性质,考虑“模特”函数为余弦函数,再利用具体函数来解决客观问题。 解题时,借助函数的奇偶性选取三角函数,利用三角函数的周期关系得到相应的系数。
三、对数函数模型

四、三角函数模型



