例说换元法在解题中的应用
■徐 政
换元法又称辅助元素法、变量代换法。通过引进新的变量,可以把分散的条件联系起来,把隐含的条件显露出来,或者把条件与结论联系起来,变为熟悉的形式,从而使复杂的计算或证明得到简化。
一、最值问题
例1 (1)实数x、y满足4x2-5xy+4y2=5,设
(2)求函数f(x)=sinx+cosx+sinx·cosx,x∈R 的最小值及取得最小值时x的值。

评注:在三角恒等变换中,有时可以把一个代数式整体视为一个“元”来参与计算和推理,这个“元”可以明确地设出来,但要注意新元的取值范围。
二、参数的值问题
例2 设a≥0,若y=cos2x-asinx+b的最大值为0,最小值为-4,则a+b的值为____。

评注:解含参数的一元二次函数在区间上的最值问题,应按照对称轴与区间的相对位置进行讨论。
三、恒成立问题
例3 已知函数g(x)=ax2-2ax+1+b(a≠0,b<1)在区间[2,3]上有最大值4和最小值1,设函数若不等式f(2x)-k·2x≥0在x∈[-1,1]上恒成立,则实数k的取值范围为_____。
解:g(x)=a(x-1)2+(1+b-a)。

评注:函数是方程与不等式的“中介”,它们既有区别,又联系紧密。对于含参数不等式的恒成立问题,可通过分离参数,使问题转化为函数的最值问题进行求解。
四、探索性问题
例4 已知函数f(x)=loga(3-ax),是否存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,且最大值为1? 如果存在,求出a的值;如果不存在,请说明理由。
解:由函数f(x)=loga(3-ax),令t(x)=3-ax。因为a>0,且a≠1,所以函数t(x)为减函数。
因为f(x)在区间[1,2]上为减函数,所以y=logat为增函数,所以a>1。当x∈[1,2]时,t(x)的最小值为3-2a,f(x)的最大值为f(1)=loga(3 -a),所以解得故不存在这样的实数a,使得函数f(x)在区间[1,2]上为减函数,且最大值为1。
评注:涉及复合函数f[g(x)]问题,常用换元法,可使问题简化处理,但要注意换元后新元的取值范围。
五、函数的零点问题

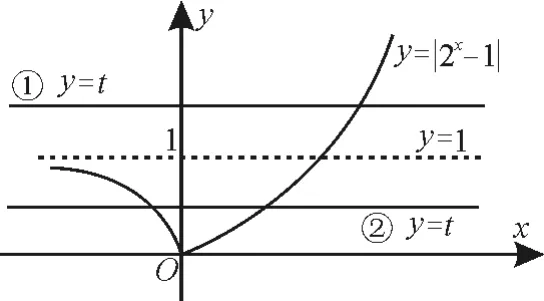
图1
要使原方程有3 个实根,只需方程t2-(2+3k)t+2k+1=0在(0,1)和[1,+∞)上各有1个根。令φ(t)=t2-(2+3k)t+2k+1,t> 0。 由 题 意 得即解得k>0。
特别地,当φ(1)=0时,k=0,此时方程t2-(2+3k)t+2k+1=0 只 有1 个 根1,不符合题意。
综上可知,当k>0,即k∈(0,+∞)时,原方程有3个不同的实数解。
评注:方程根的分布问题,可转化为函数图像的交点问题。本题重在对问题中变量的动态研究,通过解不等式使得问题圆满获解。

