Topological states switching and group velocity control in two-dimensional non-reciprocal Hermitian photonic lattice
Yu Lin(林宇), Yuandan Wang(王元旦), Junhao Yang(杨俊豪), Yixuan Fu(符艺萱), and Xinyuan Qi(齐新元)
School of Physics,Northwest University,Xi’an 710127,China
Keywords: Dirac point,imaginary coupling,Chern number,group velocity
1.Introduction
In recent years, topological photonic systems have attracted much attention from researchers,who have performed extensive studies on different topological photonic systems and achieved rich research results.[1]The study of topological photonic systems started in 1979, with the one-dimensional(1D) Su–Schrieffer–Heeger (SSH) model proposed by Suet al.[2]as a representative example, which realized topological phase transition through staggered coupling in the lattice.[3,4]Based on this,topological photonic devices have gradually attracted attention.[5–7]The SSH model has chiral and particle–hole symmetries,[8,9]and many novel phenomena have been discovered by studying the SSH model, such as topological invariants, topological phase transitions, edge states, etc.[10]With the progress of research,two-dimensional(2D)topological photonic systems have aroused great interest.[11]Quantum spin Hall effect (QSHE) and quantum valley Hall effect (QVHE) with time reversal symmetry can be realized in 2D photonic crystals.[12]QSHE can be realized in photonic crystals with strong spin–orbit coupling,[13]where spinup and spin-down bands are inverted and separated by a band gap,[14]each spin sector having a nonzero Chern number with opposite signs.Therefore, there exist topologically protected edge states propagating along the system boundary, with opposite spins and directions.These edge states are immune to disorder-induced backscattering.QVHE can be realized in photonic crystals with honeycomb or hexagonal lattices,[15]where valleys correspond to two inequivalent Dirac cones atKandK′points.By introducing a staggered potential or breaking the sublattice symmetry,[16–18]a band gap can be opened at the Dirac points (DPs), and valleys acquire opposite Chern numbers.[19]Therefore,there exist topologically protected edge states propagating along the system boundary,[20,21]with opposite pseudospins and opposite group velocities.Both QVHE and QSHE based photonic topological insulators(PTIs)preserve time-reversal symmetry,and moreover,these PTIs can also host higher-order topological phases, such as second-order PTIs with corner states or third-order PTIs with hinge states.[22–26]In 2008,Haldane and Raghu proposed a method of breaking time reversal symmetry using magneto-optical materials,[27,28]which can realize oneway transmission of chiral edge states of light.[29,30]Wanget al.,successfully observed the robust one-way transmission of edge states in a 2D magnetic photonic crystal experiment.[31]However, most of the aforementioned 2D photonic systems require the time reversal symmetry breaking,[32]and are non Hermitian.[33–38]The studies in 2D non-reciprocal Hermitian photonic systems are still rarely reported.
In this paper,we constructed a 2D non-reciprocal Hermitian photonic lattice and studied theoretically and numerically the system’s topological states and group velocity control.By changing the coupling coefficients,we analyzed the movement of DPs in the energy band structure,and the transformation between any topological states corresponding to different Chern numbers.Finally,we studied the impact of the topology on the group velocity.
2.Topological state and dispersion curve
This section presents a 2D non-reciprocal coupled Hermitian photonic lattice and its unique properties.Figure 1 illustrates the structure of this lattice, which consists of two straight waveguides,An(blue) andBn(red), forming a unit cell (red dashed box).Each unit cell has an imaginary coupling coefficient±iγbetween the two sublattices.The system can be modeled by coupled mode equations for the amplitudesanandbnof the sublatticesAandB,respectively:
wherenis the number of cells;∆is the intralayer coupling coefficient;the interlayer coupling within a cell is non-reciprocal coupling with different imaginary coupling coefficientst±iγ;the interlayer coupling between cells isδandσ.zrepresents the propagation distance of the wave packet,an,bnare the field amplitudes of waveguidesAn,Bn.
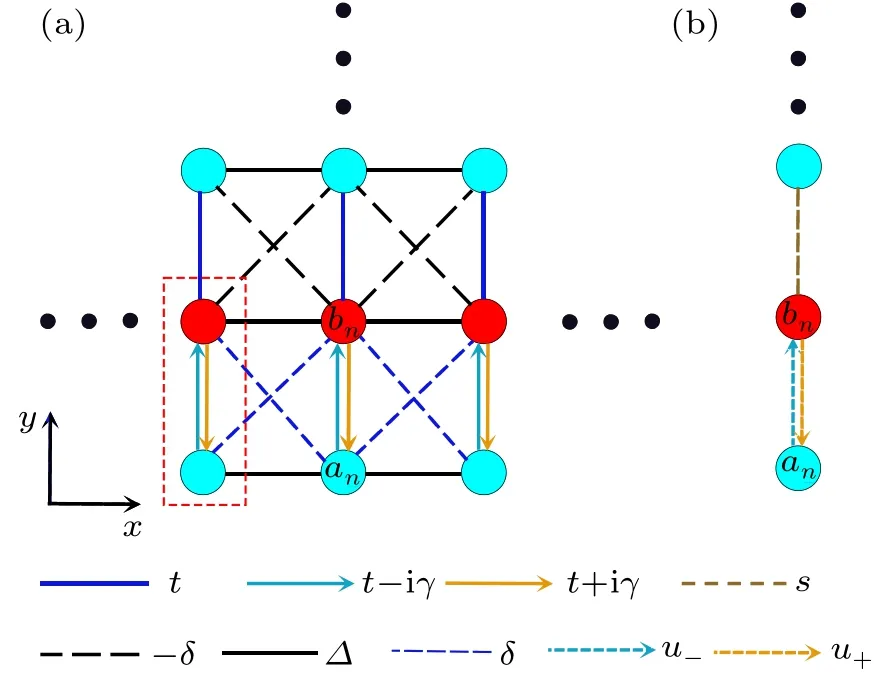
Fig.1.(a)Schematic diagram of a 2D non-reciprocal Hermitian photonic lattice with two sites per cell.(b)The effective 1D chain structure of the model in(a).
For reduction of calculation, we simplify the Bloch Hamiltonian of the system to a 1D narrow-band chain model that is periodic alongxand confined alongy.Applying Bloch’s theorem:an+1=aneik,bn+1=bneik.In the momentum space,the equation can be written as
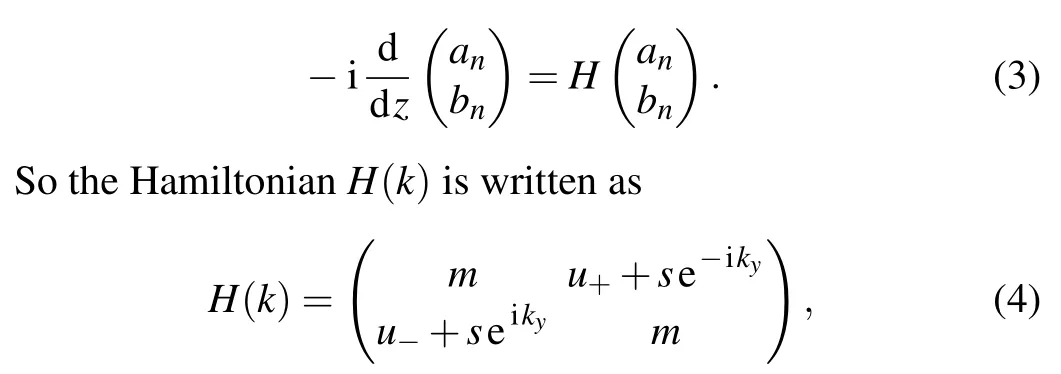
wherem= 2∆coskx;s=t-2σcoskx;u±=u±iγandu=t+2δcoskx.For a givenkx, wheng/=0 andu-/=u+,equation (4) describes a 1D narrow-band chain model with non-reciprocal intra-cell coupling,as shown in Fig.2(b).Analyzing the Bloch Hamiltonian reveals that it satisfiesH†=H,indicating that the system is a Hermitian system with real energy spectra.
The dispersion relation can characterize and predict light transmission behavior in periodic photonic crystals.The Bloch Hamiltonian is given by Eq.(4), and a solution of the equation gave the dispersion relation, which was the expression of the system’s energy band structure
The dispersion relation can characterize and predict a 2D Brillouin zone (BZ).We divide it into several small squares and calculate each square’s Berry curvature.We use the Chern number efficient method to simplify the calculation to solve whether the system has topological properties and transform the Berry curvature integral into a linear algebra problem.[49]This method is based on the Haldane model,[39–41]which assumes that the Hamiltonian can be expressed as
whereσiis the Pauli matrix anddi(k)is the real function.For such Hamiltonian quantities, the Berry curvature can be expressed as
whereεijkis the Levi–Civita notation.The Berry curvature can be transformed into a linear problem by fittingdi(k)with a cubic function
whered(k)=[d1(k),d2(k),d3(k)]andCis a constant.This linear problem can be solved by computing the dot product of[d(k)×∇kd(k)]·CandC, and then integrating the result to obtain the Berry curvature.Finally,the Chern number can be calculated by substituting the Berry curvature into the integral formula for the Chern number.
The 2D non-reciprocal Hermitian system can be solved for whether it has topological properties by the above stale efficient method.We solve the topological states of the system separately whenδ=σandδ/=σ.Whenδ=σ,the coupling coefficient∆=0,t=0.5 are fixed,and the Chern number of the system is calculated.The state is determined numerically,and the calculation results show that when the coupling coefficientδ=0.5 andγ=0,C=-2, corresponding to a topological non-trivial state;when the coupling coefficientδ<0.5 andγ>0.3,C=-1, corresponding to another topological non-trivial state; when the coupling coefficientδ>0.5 andγ>0.3,C=0, corresponding to a trivial topological state.The robustness of the topological state is further calculated,and it is found that the topological state remains unchanged when∆∈[0,0.1].
Whenδ/=σ, the coupling coefficient∆=0.5,δ=-1,t=2,σ=1 is fixed, and the Chern number of the system is calculated.It is found thatC=0, regardless of the value of the imaginary coupling coefficientγ, implies that the system is in a topologically trivial state.For a fixed coupling constant∆=0,δ=-1,t=2,σ=1,the band structure of the Bloch HamiltonianH(k)is shown in Figs.2(a)–2(c),where we plot the dispersion relation as a function of the wave vectorskxandky.
When the intralayer coupling constant∆=0,the system is chiral symmetric and preservesCH(k)C-1=-H(k).The band structure of the Bloch Hamiltonianγ=0 is shown in Fig.2(a);due to the chiral symmetry of the system,the upper and lower bands are symmetric,and there are two band inversion points at(kx,ky)=(π/2,π/2),(kx,ky)=(-π/2,-π/2).Because of the imaginary coupling constantγ=0, the bands are also symmetric about the origin,and there are three DPs located at the edge(A2,A3)and center(A1)of the BZ,with the edge DPs being symmetric about the origin (kx,ky)=(0,0).The 2D Dirac states reported to date are distributed only at high symmetry points in the BZ,and the low-energy dispersion of these Dirac states is isotropic due to symmetry constraints.Ref.[42] reported in 2022 that the Dirac states in antimony films are located at general momentum points.

A DP at a non-high-symmetry point of an optical system can be realized by adjusting the imaginary coupling coefficient in a 2D photonic crystal,as shown in Fig.2.When the imaginary coupling coefficient increases gradually toγ=0.3, the DP shifts from the edge of the BZ to the center of the BZ,and the DP at the center breaks.Under this condition,there is only one non-high symmetry DP,The imaginary coupling coefficient can be interpreted as a phase factor that modifies the hopping amplitude between neighboring sites in the photonic crystal.This phase factor violates the time-reversal symmetry and leads to a non-reciprocal propagation of light.Consequently, the dispersion relation is distorted and shifted by the imaginary coupling coefficient.The DP,which is a degenerate point of two bands with opposite parity, is sensitive to the phase factor and can be manipulated or split by tuning the imaginary coupling coefficient.The band gap,which is determined by the band inversion between the two bands, is also influenced by the imaginary coupling coefficient.When the imaginary coupling coefficient is sufficiently large, the band inversion can be reversed and the band gap can be opened.as shown in Fig.2(b).When the imaginary coupling coefficientγincreases further,we find that the DP moves wholly and again breaks.The band gap widens with the rise of the imaginary coupling coefficient.By adjusting the coupling coefficient,we provide a simple model and method to locate the 2D DP at a general momentum point.
Figure 2(d)shows the band structure forδ=σ=t=0.5.Due to the chiral symmetry of the system,the upper and lower bands are symmetric, and there is no degenerate point in the design,only two band sharp points.When the intralayer coupling coefficient∆=0.1, the chiral symmetry of the system is broken.In Fig.2(e), due to the breaking of chiral symmetry,the balance of the upper and lower bands is destroyed,but the two band abrupt points at(kx,ky)=(π/2,π/2),(kx,ky)=(-π/2,-π/2)are not broken due to the breaking of symmetry,and as∆increases,the maximum value of the band in the range ofkx=-π/2 tokx=π/2 andky=-π/2 toky=π/2 increases,and the maximum value of the band in the range ofkx=|π/2|tokx=|π|andky=|π/2|toky=|π|decreases.By adjusting the coupling coefficient,we provide a simple model and method to make the 2D DP at a general momentum point.
When the system is in the topologically non-trivial state corresponding toC=-1,the band structure shows that,compared with the topological state corresponding toC=-2,the overall dispersion relation decreases inward, and the maximum value of the dispersion relation is lower.Nevertheless,the broadband sharp points do not disappear, as shown in Fig.2(f).
A comparison of the six band diagrams reveals that there are always two sharp points in each band and that their positions do not depend on the imaginary coupling coefficientγ.The analytical solution indicates that the strong points are located at(kx,ky)=(π/2,π/2)and(kx,ky)=(-π/2,-π/2).
3.Research on topological states
However, not all topological systems exhibit consistent boundary state behavior under open boundary conditions.[43,44]Therefore, in specific studies, the system structure and boundary conditions must be considered to determine the energy spectrum of topological systems under open boundary conditions.
When the intralayer coupling coefficient∆=0 and the other coupling coefficients areγ= 0,δ= 0.5,t= 0.5 andσ=0.5, the system is in the topological state when Chern numberC=-2.Figure 3(a)shows the energy spectrum structure of the system with an open boundary in theydirection and an even number of lattice points, assumingny=40 andNy=80.There are zero energy degenerate bands in the energy spectrum of the system and several particular degenerate points in the bulk state.The numerical solution indicates that the positions of these points arekx=±1.04,±2.08,where there are four-fold degeneracies ofnyand the intracell couplingu±vanishes,that is,t+2δcoskx±iγ=0,as shown by the blue dashed line and the intersection point with the bulk state.If an odd number of lattice pointsNy=81 is chosen in theydirection, a flat band appears in the open boundary energy spectrum throughout the BZ,as shown in Fig.3(d).
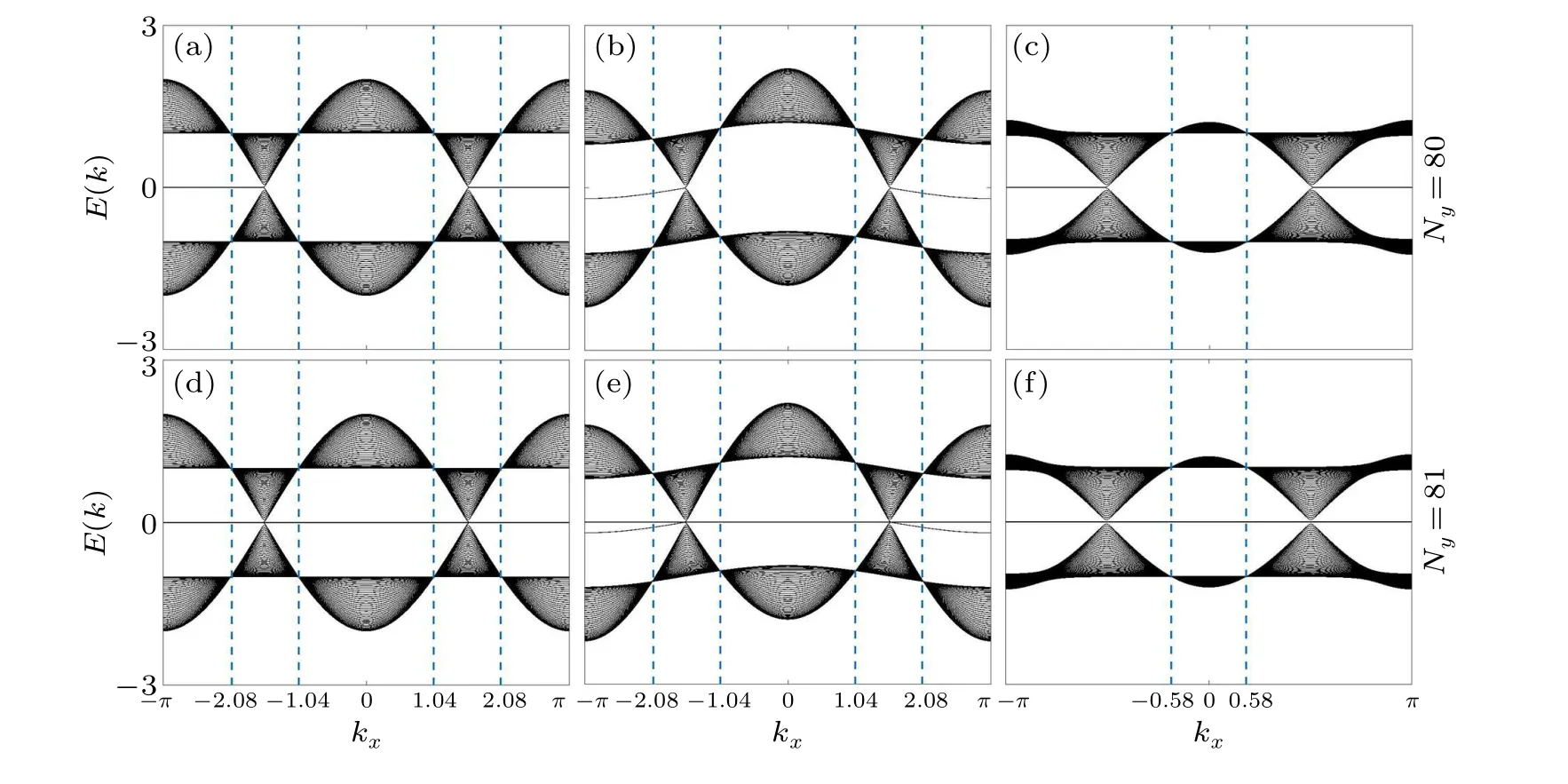
When the intralayer coupling coefficient∆= 0.1, figures 3(b) and 3(e) show the change of the energy spectrum structure of the open boundary in theydirection when the intralayer coupling coefficient∆/=0.Figure 3(b) is the energy band diagram when the number of lattice points is even(Ny=80),indicating that when the intralayer coupling coefficient∆changes within a small range,it has a particular impact on the energy spectrum of the whole system.First,it changes the edge state of the system, making it from a topologically protected zero mode to a topologically protected near-zero way; second, it changes the symmetry of the system, making the upper and lower energy spectra no longer symmetrical but does not affect the position of the degenerate points in the bulk state.The bulk state is still decayed atkx=±1.04,±2.08.For the energy band diagram with an odd number of lattice points(Ny=81), the change of the energy spectrum diagram is consistent with Fig.3(d), and a zero-energy flat band appears throughout the BZ.The appearance of these states is closely related to the specific shape and topological properties of the lattice.However,increasing the number of lattice points does not change the existence and position of bulk degenerate points and topological edge states because the appearance of these states depends on the specific shape and topological characteristics of the lattice rather than just the increase in the number of lattice points.
In general, the intralayer coupling coefficient∆affects the edge state of the system: when the intralayer coupling coefficient∆=0,the edge state of the system is a topologically protected zero mode;when the intralayer coupling coefficient∆/=0,the edge state of the system is a topologically protected near-zero mode.
The number of lattice points in theydirection affects the appearance of the zero-energy flat band in the open boundary energy spectrum,regardless of whether the system is topologically trivial or non-trivial.No flat band appears in the whole space when the number of lattice points in theydirection is even.When the number of lattice points in theydirection is odd,the zero-energy flat band always exists,regardless of how the coupling coefficients change.[45,46]In summary, we propose a method to realize a flat band at a single lattice point without considering the amplitude and phase of the lattice points.
Figure 3 has simplified the 2D photonic crystal into a 1D non-reciprocal narrow-band chain model along theydirection.This narrow-band chain model simulates the light wave transmission behavior.
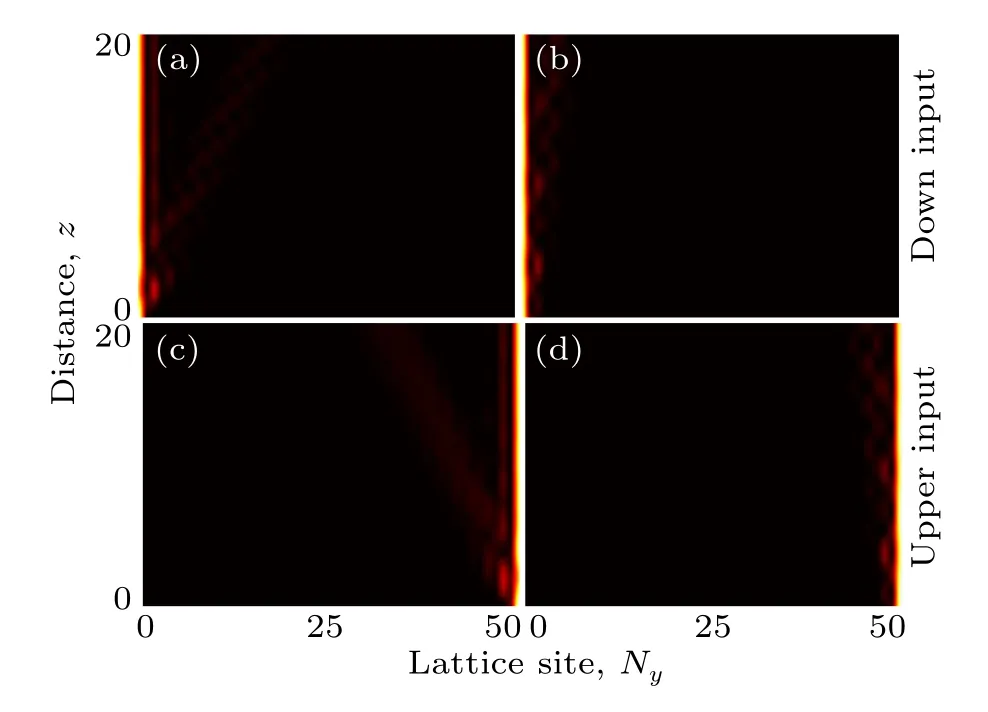
Figure 4 illustrates the light wave transmission process at the boundary of a finite system under the topologically nontrivial condition.Assumingy=25, the number of lattices isNy=2ny=50,the wave vectork0=π,and a Gaussian wave packet is used for excitation.Figures 4(a) and 4(c) show the evolution of the edge states under topological non-trivial condition when the system’s Chern numberC=-2,with the coupling coefficients∆=0,δ=0.5,t=0.5,σ=0.5,γ=0.We observe topological edge states at the upper and lower waveguide edges, and the waveguide is localized on the outermost waveguide.Figures 4(b) and 4(d) show the evolution of the edge states under topological non-trivial condition when the system’s Chern numberC=-1,with the coupling coefficients∆=0,δ=0.3,t=0.5,σ=0.3,γ=0.1.We observe that the light wave oscillates and couples with other waveguides, but due to the topological property of the system, the light wave eventually localizes on the edge waveguide,which is the topological edge state.
4.Study on group velocity control
This section investigates how to control the photonic crystal’s group velocity by tuning the system’s coupling coefficients.The group velocitieskxandkyof the wave packet along thexandydirections,respectively,are obtained by solving the first-order derivatives of Eq.(8)concerningvkxandvky.
The formula for the group velocityvkxis derived as follows:
whereA=(-2∆±(1+eiky)2t(δ-σ)-(-1+e2iky)iγσ ∓4(eikyδ-σ)(-δ+ eikyσ)coskx)),B= e2iky(t+ iγ+2δcoskx)(t-2σcoskx),C= eiky(2t2+γ2+2(δ2+σ2)),D=4t(δ-σ)+4t(δ-σ)coskx+2(δ2+σ2)cos2kx),E=t2-iγt-2δσ+2tδcoskx+2iγσcoskx.
Figure 5 shows how tuningγ,an imaginary coupling coefficient in our system, affects group velocities alongx.Figures 5(a)–5(c) illustrate howvkxvaries withkxfor different values ofγ.Whenγ=0,there are three points wherevkx=0,corresponding to the edge and center of the BZ.The band jump point in the band structure remains a discontinuity invkxregardless ofγ.Whenγ=0.3,vkxchanges slightly: it becomes flatter around the center point and reaches higher maxima and lower minima.Asγincreases further, these trends continue:vkxbecomes more gentle at the center and more extreme at other points.Increasingγdoes not affect the zero group velocity points.Still, it causesvkxto increase or decrease continuously depending onkxand become flatter at the center.Figure 5(d) showsvkxunder topological conditions.There are still three points wherevkx= 0, as in the non-topological case, but there is no abrupt change at the band jump point; instead, two group velocity bands intersect at(kx,ky,vkx)=(±π/2,±π/2,0).The overall variation ofvkxis also significantly reduced due to topological suppression.

Fig.5.Group velocity control in the x direction.(a)–(c) The group velocity variation curves for the topologically trivial state, with the same parameters as Figs.2(a)–2(c).(d)The group velocity variation curve for the topologically non-trivial state,with the same parameters as Fig.2(d).
The formula for the group velocityvkyis derived as follows:
Figure 6 shows the group velocity variation curve in theydirection.Figures 6(a)–6(c) illustrate how increasingγaffectsvky.Unlikevkx,vkyis not zero at the edge of the BZ; it has a value of 50 whenγ=0.Asγincreases,vkydecreases at most points except for the center point, where it remains zero.The slope around this point is also tiny and close to zero,which may result in localized or dispersion-less transmission of light waves.In addition,vkyis negative for most values ofkyin in the range of 0 toπ,indicating group velocity deceleration.Thus,we observe group velocity acceleration,deceleration,and zero group velocity within one period.Increasingγdoes not change these phenomena significantly;it only causesvkyto decrease further.Figure 6(d)showsvkyunder topological conditions.The variation ofvkyis tiny under this condition;only near(0,0)is there a noticeable curvature that may cause light wave diffraction due to topological suppression of group velocity variation.
5.Conclusion
As one of the most attractive optical systems for light manipulation, non-reciprocal photonic lattices provide abundant means to realize the topological edge states and regulate the group velocity.This paper presents a theoretical design of the non-reciprocal Hermite 2D photonic lattice, and the topological phase transition, topological edge state, optical transport behavior,and group velocity change in the non-reciprocal coupling photonic lattice are studied.The research results show that when the imaginary coupling coefficientγ<0.3 and interlayer coupling coefficientδ<0.5,the system has a topologically non-trivial state ofC=-1;when the imaginary coupling coefficientγ=0 and the interlayerδ=0.5,the system has a topologically non-trivial state ofC=-2.When the imaginary coupling coefficientγ=0,the system energy band is symmetric relative to the wave vector (kx,ky)=(0,0).In a finitely large system,the system has a zero-energy flat-top band when the lattice number in the directionyis odd.The study of group velocity shows that zero group velocity points exist regardless of the topological property of the system.However,the topological state can suppress the amplitude of the group velocity profile.To sum up, this work realizes different topological states of system and localized states of light waves in 2D photonic lattices,enriches the connotation of optical transmission and group velocity regulation in 2D non-reciprocal Hermitic photonic lattices, and has particular theoretical guiding significance in the fields of optical communication and photonic device fabrication.[47,48]
Acknowledgment
Project supported by the National Natural Science Foundation of China(Grant No.1217040857).
- Chinese Physics B的其它文章
- The application of quantum coherence as a resource
- Special breathing structures induced by bright solitons collision in a binary dipolar Bose–Einstein condensates
- Effect of short-term plasticity on working memory
- Directional-to-random transition of cell cluster migration
- Effect of mono-/divalent metal ions on the conductivity characteristics of DNA solutions transferring through a microfluidic channel
- Off-diagonal approach to the exact solution of quantum integrable systems

