The application of quantum coherence as a resource

Si-Yuan Liu(刘思远) and Heng Fan(范桁)

1Institute of Modern Physics,Northwest University,Xi’an 710127,China

2Shaanxi Key Laboratory for Theoretical Physics Frontiers,Xi’an 710127,China

3Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

4School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

5CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

6Beijing Academy of Quantum Information Sciences,Beijing 100193,China

Keywords: quantum coherence,quantum computing,quantum information,quantum thermodynamics,quantum biology

1.Introduction

Quantum coherence describes the superposition of different states of quantum systems and plays a very important role in quantum information science.In 2014, Baumgratzet al.proposed a theoretical framework for quantitative research on quantum coherence from the perspective of resource theory.[1]Since then, the coherence theory based on this theoretical framework has developed explosively.Based on the view of Baumgratzet al.,coherence is different from entanglement.It is a physical resource related to the selection of basis vectors.After the reference basis is selected,the free state is a quantum state diagonalized under this set of reference bases and called an incoherent state.Otherwise,the quantum state is a coherent state.

The next key problem is how to describe coherence mathematically,which is crucial for studying the role of coherence in quantum systems.And it is also a basis for further study of quantum coherence and quantum correlation.Baumgratzet al.proposed a quantum coherence measurement scheme based on the resource theory framework and four criteria that quantum coherence measure functions must meet.[1]Respectively:(A1) Non-negativity, the coherence should be zero for all incoherent states.(A2a) Monotonicity under incoherent completely positive and trace preserving maps.(A2b)Monotonicity under selective measurements on average.(A3) Convexity, nonincreasing under mixing of quantum states.Based on these criteria, they proposed the relative entropy andl1-norm coherence measure functions.Inspired by the pioneering work of Baumgratzet al., a series of other quantum coherence measure functions that meet the above criteria have been proposed, for example, coherence measures based on quantum entanglement,[2]coherence robustness,[3]coherence weight,[4]coherence of skew information,[5]and coherence measures based on convex top combination.[6–8]By changing the four criteria proposed by Baumgratzet al.,some other possible coherent metric functions were also considered.[9]

In order to further explore the physical significance of coherence measures, it is necessary to study the relationship between coherence and other quantum resources.Coherence resource theory benefits from the inspiration of entanglement theory.There are several connections between them,for example, geometric coherence[10]and geometric entanglement[11]based on fidelity,coherence of formation[12]and entanglement of formation,[13]genuine multipartite coherence[14]and genuine multipartite entanglement.[15]In addition, in Ref.[11],the author studied the transformation relationship between coherence and entanglement and proposed coherent monotonicity based on entanglement.On the other hand, entanglement can also be quantified by coherence.Tanet al.proved that entanglement monotonicity can be established by using the symmetric part of correlation coherence.[16]In addition, Chitambaret al.investigated the relationship between coherence and entanglement from the perspective of resource purification and quantum state construction.[17]They analyzed the task of purification or state construction of coherence and entanglement simultaneously under the local incoherent operation supplemented by classical communication.The conversion rates for purifying and constructing quantum states under asymptotic limit conditions were given.This reveals how local coherence and global entanglement affect each other.The above relationships all reveal the internal connections between coherence and entanglement.

In addition to studying various measurement schemes,quantum coherence as a useful physical resource is also very fragile.It is highly susceptible to interference from the surrounding environment and leads to decoherence.Therefore, scientists have also conducted extensive research on the evolution and maintenance of quantum coherence in open systems.[1,18,19]In particular, it is found that thel1-norm coherence and relative entropy coherence of some noisy channels are frozen in the evolution process.[20]The evolution of quantum coherence for specific noise channels also satisfies the decomposition rate of evolution.[21]In addition,the coherent generation and coherent destruction ability of some channels were also studied.[22]

Quantum coherence has been found to play an important role in many quantum processes since it was proposed.For example,quantum coherence is the cause of quantum interference, as well as nonlocality, quantum steering, quantum entanglement, quantum discord, and other two-body and manybody quantum correlation phenomena.More importantly, as the key theory driving quantum technology, quantum coherence needs to be regarded as a physical resource for further research.[23–26]And now it has been widely used in quantum computing, quantum information, quantum thermodynamics,quantum biology,etc.

Quantum computing with the help of coherence can achieve many tasks that are impossible or difficult to accomplish with classical information processing.[27–30]Quantum computing depends on the processing of information qubits that may be in a superposition state.And maintaining coherence is also very important for quantum algorithms and quantum parallel processing.[31]In 1992, David Deutsch and Richard Jozsa proposed the first quantum algorithm, the Deutsch–Jozsa quantum algorithm (D–J algorithm).[32]This was the first algorithm to demonstrate the significant differences between quantum computing and classical computing in solving specific problems.In addition, when the D–J algorithm solves the decision problem between two candidate schemes, decoherence will reduce the decision-making ability of the algorithm.The smaller the coherence in the system,the lower the ability of the algorithm to distinguish the two cases.[33]Quantum coherence also plays an important role in Grover search algorithms.[34,35]Anand and Pati investigated a Grover-like algorithm and established the relationship between the search success probability and its corresponding quantum state coherence value.[36]In 2017, Shiet al.investigated the role of quantum coherence depletion(QCD)in the Grover search algorithm and found that the success probability depends on the QCD.[37]Another important quantum algorithm is known as the deterministic quantum computation with one qubit (DQC1).[38]DQC1 challenges the idea that only pure states can perform quantum calculations with exponential acceleration.It also opens up a new direction for the experimental implementation of quantum computing.And it was found that single qubit quantum computing also needs coherence.In particular, Materaet al.showed that the precision of the algorithm is directly related to the recoverable coherence.[39]In addition,a large number of studies have confirmed that quantum walking is a tool for designing quantum algorithms, especially the design of search algorithms.In 2003, Shenvi proposed the quantum random walk search algorithm.[40]In 2018,Suet al.studied the role of coherence systemically in a quantum walk search algorithm.[41]They found that the consumption of coherence represents an increase in the success probability of the searching.Coherence is also very important in the realization of quantum computing.However,no quantum system can be completely isolated.In the process of evolution, the system will become decoherent with the environment coupling.So how to maintain its coherence and improve the decoherence time has become an important open question.In recent years, this field has received extensive attention and research, which has promoted the development of quantum computing.With the development of quantum information science,the role of quantum coherence in information processing has also been investigated extensively.Coherence is also closely related to parameter estimation in quantum metrology.[42]In some common parameter estimation schemes,coherence is the premise of efficient detection.[43]In addition, when parameters are estimated, the maximally coherent state can make the accuracy of parameter estimation exceed the limit of classical estimation.[44]In quantum channel discrimination, the existence of coherence of a detection state will increase the success rate of identification, and the degree to which the recognition success rate increases can be described by the coherent robustness.[45,46]In the related research of quantum phase transition,it is found that some quantum phase transitions can be detected by quantum coherence.[47–49]For example, Karpatet al.found that in the anisotropic spin-1/2XYchain in the transverse magnetic field,the local coherence is related to the critical point of second-order quantum phase transition in theXYmodel.[47]

Last but not least,quantum coherence also plays a significant role in interdisciplinary research.The role of quantum coherence in quantum thermodynamics and quantum biology is briefly introduced.In recent years, with further study of quantum thermodynamics, people have found that coherence is closely related to the efficiency of some quantum heat engines.For example,Scullyet al.studied the effect of quantum coherence on the efficiency of a photon Carnot machine.[50]It is confirmed that quantum coherence can be used as a resource to improve the efficiency of a heat engine.Rahavet al.found that coherence also affects the performance of quantum heat engines and the heat exchange between heat engines and reservoirs.[24]In addition, coherence is also considered as an important resource for extracting work from thermodynamic tasks.[19,25]Moreover,in quantum biology,[51–54]there are also many studies on coherence.And as a resource,more and more research shows that coherence plays a vital role in the quantum process.Further research on the resource theory of coherence has far-reaching significance for people to understand and manipulate quantum systems.

The organization of this paper is as follows.In Section 2,we discuss the utilization of quantum coherence in quantum computing, mainly including quantum algorithms, decoherence in superconducting quantum computing and quantum simulation.In Section 3,we introduce the application of quantum coherence in quantum information, including quantum metrology, quantum simulation, quantum channel discrimination, witnessing quantum correlations and quantum phase transitions.In Section 4, we briefly report on the role of coherence in interdisciplinary studies.In Section 5,we conclude with a summary and discussion of some currently open issues in the theoretical description of coherence and its role in quantum physics.

2.Application of quantum coherence in quantum computing

2.1.Quantum algorithm

Compared to traditional computers, quantum computers utilizing quantum resources such as quantum coherence can greatly improve computational efficiency and solve tasks that classical computers cannot complete.The development of quantum computers depends on quantum algorithms, which are also related to quantum coherence.Therefore, it is very meaningful to study the role of quantum coherence in quantum algorithms.Next,we will use a series of typical examples to illustrate some of the main developments in this field.

2.1.1.Deutsch–Jozsa algorithm

The Deutsch–Jozsa algorithm,[32]which is the earliest algorithm in quantum algorithms,was proposed by Deutsch and Jozsa in 1992.Although the problems it can solve are very limited,it effectively demonstrates the advantages of quantum computing over classical computing.If a Boolean function has only two possibilities: constant values(for the entire domain,the function values are either all 0 or all 1) or balanced values(exactly half of the function values are 0 and the other half are 1),to distinguish between these two possibilities,classical computers need up to 2N-1+1 function values.ForN-qubit quantum systems, the Deutsch–Jozsa algorithm only requires 1 function value to achieve this.In 2016, Hillery discussed the impact of quantum coherence on the Deutsch–Jozsa algorithm numerically by observing the impact of decoherence on the performance of the Deutsch–Jozsa algorithm.[33]He usedl1-norm to measure coherence and multiple different metrics to measure algorithm performance.It was found that decoherence reduces the ability of the algorithm to determine alternatives.The smaller the coherence in the system, the poorer the ability of the algorithm to distinguish between these two situations.This indicates that coherence is a resource of the algorithm.In addition,the Deutsch–Jozsa algorithm was analyzed in a probabilistic setting.It was proved that when there is enough coherence present, there will be a quantum advantage.For a fixed number of measurements, one has a higher probability of making the correct decision using quantum procedures than by using classical procedures.

2.1.2.Grover algorithm

The Grover search algorithm is a unique algorithm among all quantum algorithms.It has great significance and plays an important role in quantum computation.The basic principle of this algorithm was proposed by Grover in 1997.[34]The Grover search algorithm is mainly used to address the following issues.For example, given a search space of sizeN,prior to this,there was no knowledge of the structural performance of this space in all aspects.But we still hope to find an element in this space that satisfies the properties we have set.Generally, in classical algorithms, finding this unique element requiresNoperations.However, through the Grover search algorithm,it usually only needs√Noperations to solve this problem.In 2016,Anand and Pati systematically investigated the behavior of quantum coherence in the discrete analogue of the analog Grover search algorithm.[36]The analog Grover search algorithm is a continuous time quantum algorithm based on the adiabatic Hamiltonian evolution that gives a quadratic speed-up,similar to the original Grover search algorithm.They found that the decrease of quantum coherence,quantified using various coherence monotones, is a clear signature of attaining the maximum success probability in the analog Grover search algorithm.They also found that for any two qubit reduced density matrix of the system,the evolution of concurrence is very close to the increase of success rate,and established the relationship between the search success probabilityPsuccand its corresponding quantum state coherence value,

Figure 1 shows the changes ofl1-norm, relative entropy of coherence and the success probability of the Grover search algorithm with time.It can be observed analytically from Eqs.(1) and (2) and numerically from Fig.1, that the probability of Grover search algorithm success gradually increases over time, while quantum coherence gradually decreases under thel1-norm and relative entropy measure.When the success probability of the Grover algorithm reaches 1, the two coherence measures tend to 0,which indicates that the Grover search algorithm has been successfully evolved,and quantum coherence is an effective resource of the Grover search algorithm.It was also shown that a maximally coherent state ends up into an incoherent state as the Grover search algorithm evolves andn-maximal coherence is actually consumed during the search process.Hence quantum coherence acts as a clear signature for the success of the Grover search algorithm.

Fig.1.Variations of the l1-norm,the relative entropy of coherence and the probability of success as a function of time.Reproduced with permission from Ref.[36].

In 2017, Shiet al.investigated the role of quantum coherence depletion in the Grover search algorithm by using several typical measures of quantum coherence and quantum correlations.[37]By using thel1-norm and relative entropy of coherence measure(Cl1,Cr),they found that the success probability depends on the QCD.In the limit case,the relationship between the search success probability and its corresponding quantum state coherence value is as follows:

In the limit case, they also defined the cost performance to characterize the behavior of QCD in enhancing the success probability of the Grover search algorithm and represented it as

wherejandNrepresent the number of solutions and the scale of the database.They found that the cost performanceωis only related to the number of searcher items and the scale of the database respectively,no matter whetherCrorCl1is used.

2.1.3.DQC1

Knill and Laflamme proposed a mixed state quantum computing model in 1998,[38]which is ann+1 qubit model.In the initial state,except for the first qubit with polarization,all othernqubits are in the maximum mixed state.This quantum algorithm provides an exponential speed-up over the best known classical procedure for estimating the trace of a unitary matrix.And DQC1 challenges the idea that only pure states can perform quantum calculations with exponential acceleration.It also opens up a new direction for the experimental implementation of quantum computing.

After the DQC1 algorithm was proposed,scientists were committed to reconsidering what makes quantum computing different from classical computing.In 2005,[55]Dattaet al.studied the role of entanglement in DQC1 and found that this algorithm only requires very little entanglement.Obviously, quantum entanglement cannot explain the quantum advantage of DQC1.Later, quantum discord was proposed,which promotes the understanding of quantum correlation.[56]In 2008,[57]Dattaet al.found that quantum discord can often be observed in the calculated final state of the DQC1 algorithm.Therefore,quantum discord was likely to be the key to explaining the quantum advantage of DQC1.However, some researchers questioned the role of quantum discord for DQC1,since not all processes will result in a final state with quantum discord.The acceleration for this process cannot be explained by quantum discord.And in 2010,[58]Daki´cet al.showed that certain nontrivial instances do not involve any quantum correlations.In addition, this issue was further discussed by Datta and Shaji in 2011.[59]Others believed that DQC1’s advantage comes from its quantum gate operation’s ability to entangle some states in the largest mixed state of the first qubit and other qubits.Therefore, the reason for the quantum advantages of the mixed quantum computing model represented by DQC1 and the most important quantum computing resource are still important open questions.

Maet al.first studied the role of coherence in DQC1 in 2016.[60]In the same year, Materaet al.[61]showed how the accuracy of outcome in DQC1 can be quantified in terms of the recoverable coherence.The relationship between the accuracy of DQC1 protocol with mixed control qubit and the recoverable coherence was also given by

whereSE(x)denotes the standard error of the mean associated with the random variablex.

2.1.4.Quantum random walk search algorithm

Classical random walks provide some of the most wellknown algorithms for factorization,k-SAT, graph isomorphism and other problems.Similar to the classical continuous and discrete random walks,quantum walks can be divided into continuous time quantum walks and discrete time quantum walks.And a large number of studies have confirmed that the quantum walk is a tool for designing quantum algorithms,especially for quantum search algorithms.The quantum search algorithm constructed from a discrete quantum walk on a hypercube is similar to the Grover search algorithm.A search algorithm based on a continuous quantum walk also has similar quadratic speed-up.Both are universal computational models.Among them, discrete quantum walks include the coin quantum walk and scattering quantum walk.The coin quantum walk on the graph is defined as a walk on a vertex that requires an auxiliary coin space.Its dimension is the number of vertices.The scattering quantum walk encodes all edges of the graph into quantum states,which does not use the coin operator.Reference[6]demonstrates the unitary equivalence of these two discrete quantum walks.But the definition of the scattering quantum walk on a nonregular graph is more natural and the physical realization is more direct.The quantum walk is not only studied in theory but also realized experimentally in various ways.Now, the scattering quantum walk can be achieved using linear optical elements.And the search algorithm based on such a quantum walk is constructed and analyzed on a complete graph explicitly,which shows an analogous quadratic speed-up.

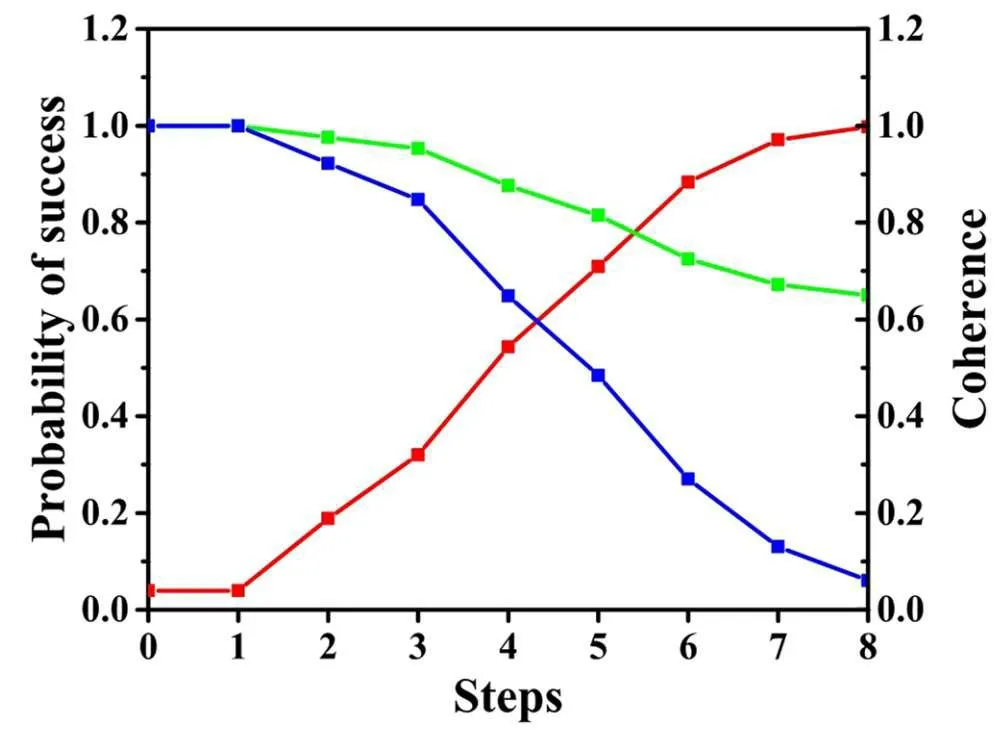
Fig.2.The number of total vertices is 100 and the number of marked vertices is 2.The phase shift is set to π.The red line is the probability of success.The green line is the coherence under Cr(ˆρ)and the blue line is the coherence under Cl(ˆρ).The values of two measures of coherence are normalized to 1.The X axis is the iterations of this algorithm.The left Y axis is the probability of success and the right Y axis is the value of the normalized measure of coherence.Reproduced with permission from Ref.[41].

2.2.Decoherence in superconducting quantum computing

With the continuous development of large-scale integrated circuits,due to the limitations of classical physical principles, the current classical computer has approached its processing capacity limit.On the other hand, the quantum computer has the advantage of fast computing speed,since it meets the principle of superposition of quantum states and the characteristics of quantum entanglement.Quantum computing not only takes a big step forward from traditional computers, but also makes the whole concept of computing take on a new look.It uses the principles of quantum mechanics and has the advantages of quantum parallel computing,which will be more effective than classical computing.The process of quantum computing is as follows.First,the information is stored on some quantum parameters(such as spin,photons,atoms,etc.)usually composed of qubits.Then these parameters interact in some ways, but it does not destroy the quantum coherence between them.Therefore, finding a suitable quantum system to realize quantum bits is the key to the problem.These systems must meet the following conditions: easy to initialize,easy to control,easy to read information,easy to couple with other qubits,and maintain coherence for a long time.[63,64]At present,the experimental schemes for the physical realization of quantum computing include a simple harmonic oscillator,photon and nonlinear optical medium,cavity quantum electrodynamics device, molecular nuclear magnetic resonance, ion trap,etc.[65]

The basic physical processes of quantum computing include the preparation, operation and measurement of qubits.[66–68]No quantum system can be completely isolated.There are universal and inevitable interactions between a real environment and a quantum system.The effects of these interactions are twofold.On the one hand, the evolution of the system may no longer be unitary or reversible.On the other hand, the system will gradually lose its original coherence due to the interaction with the environment.The decoherence effect is very important in quantum information processing,and it is one of the important factors limiting quantum computing.Increasing the coherence time of qubits will greatly improve the practicability of quantum computing, which can help us achieve the computing goal that is currently impossible.Therefore, there are three key points in the study of quantum computing.Firstly,we need to ensure that the physical processes involved in quantum computing are carried out accurately.Secondly, we should study some important basic problems, such as the coherence properties in quantum systems and the dissipation caused by the interaction between quantum systems and the surrounding environment.Thirdly,we should find out the origin and microscopic mechanism of decoherence to obtain a method to suppress decoherence.

Although superconducting quantum computing is one of the fastest developing, most powerful and most promising quantum computing solutions for integrated circuits,it is still in its infancy.Its shortcomings are mainly manifested in two aspects.The amount of quantum bit coupling that people can achieve is limited.Moreover, the coherence time is relatively short.In recent years, there have been many relevant reports on the scientific research into decoherence.For example, Fedichkinet al.studied the long-term decoherence of photoelectrons in the Markov approximation.[69]Vorojtsovet al.studied the decoherence of double quantum dot qubits in the same way.[68]Thorwartet al.investigated the long-term decoherence of double quantum dot qubits by using the quasi-adiabatic path integral method.Lianget al.discussed the short-term decoherence of a charge qubit system under Markov and non-Markov approximation by using various methods.[70]Alosh has realized the quantum lossless measurement of photon states in the cavity by using high-Q resonators.In 2021, Placeet al.fabricated a superconducting qubit new material platform with coherence time over 0.3 ms by replacing niobium with tantalum in the device.[71]In 2021,Siddiqi identified the main source of superconducting qubit decoherence by exploring pioneering qubit and resonator experiments.[72]These studies show that the understanding of the decoherence mechanism is constantly developing.In order to realize large-scale quantum computing based on superconducting qubits,it is necessary to further improve the coherence of superconducting qubits.As mentioned above,the microcosmic mechanism of superconducting qubit decoherence is not very clear,so research in this area not only has important academic significance,but also has great application prospects.

2.3.Quantum simulation

Simulating quantum mechanics is widely recognized as a challenging computational task, particularly for large-scale systems.Nevertheless,this challenge can be overcome by employing a controllable quantum system to study another quantum system that is less controllable or accessible, known as quantum simulation.[73]Quantum simulation holds great potential for investigating various problems in condensed matter physics,high-energy physics,atomic physics,quantum chemistry and cosmology.[74]Quantum simulation can be realized using quantum computers, as well as simpler analog devices that require less control and are easier to construct.When using an easy-to-control quantum system to simulate a complex quantum system, maintaining quantum coherence is the basic requirement for simulating various quantum phenomena.With the development of various quantum control technologies,the control technology for the coherence evolution of various quantum systems has made great progress,such as in the coherent manipulation of atoms in optical lattices, superconducting circuits, photons, etc.All of them push the quantum simulation forward on the road to practical application.[75]

Neutral atoms in optical lattices are highly suitable for simulating solid-state systems.The optical potential can be adjusted to allow for variations in the geometry and size of lattices.Since the pioneering experiment[76]by Greineret al.in 2002,where a cold atomic gas in an optical lattice was used to simulate the quantum phase transition from superfluid to Mott insulator, there has been a growing interest in utilizing atoms in optical lattices for the study of condensed matter physics.In a comprehensive theoretical review[77]by Lewensteinet al.in 2007, the potential of atoms in optical lattices as quantum simulators is discussed and many examples of quantum systems that can be simulated are provided.Another review[78]by Blochet al.in 2012, highlighted experimental advancements in this field.

Photons have the remarkable capability to transmit quantum information over long distances with minimal impact from noise or decoherence.They inherently possess the ability to encode qubit states, such as utilizing the polarization of photons.Moreover, implementing one-qubit gates can be achieved using linear optical components conveniently.Photons have been used to simulate frustrated Heisenberg spin systems[79]and relativistic field theories.[80]

In superconducting circuits,by manipulating the currents and voltage signals in the circuit, one can control the evolution of the quantum states.The evolution results can be measured using highly integrated devices.Although the entire setup is at the macroscopic scale,superconducting circuits exhibit atomic-like quantum behavior.Researchers have successfully demonstrated individual control and measurement of superconducting qubits.[81]Moreover, high-fidelity quantum gates involving one,two and even three qubits have been successfully demonstrated in these systems, meaning that superconducting circuits can be produced in large numbers and have great application prospects.

In addition, the dynamics of multi-particle systems in quantum systems has also been explored.Barreiroet al.[82]reported the first realization of a toolbox for simulating an open quantum system with up to five qubits.Then, Schindleret al.[83]extended the concept of dynamical maps to an open system.They experimentally explore the stroboscopic dynamics of a complex many-body spin model by means of a universal quantum simulator.Daleyet al.[84]gave an overview of the state-of-the-art and future perspectives for quantum simulation.

As one of the important applications in the field of quantum computing, quantum simulation provides us with new ways to solve problems that cannot be handled by classical computing.With the increase in the number of qubits and the development of error correction and noise control techniques,future quantum simulations will be able to handle larger-scale and more complex problems.This will allow us to delve deeper into areas such as the properties of matter,the mechanisms of chemical reactions,the behavior of condensed matter systems,etc.

3.Application of quantum coherence in quantum information

The combination of quantum mechanics and information science has produced a multidisciplinary field called quantum information science.Compared with traditional information technology, quantum information science not only shows unparalleled advantages,but also provides a revolutionary direction for its development.Moreover,the advancement of quantum information science can enhance the refinement of quantum theory and deepen our comprehension of the fundamental essence of quantum mechanics.Quantum coherence plays a key role in quantum information processing.And it is the potential cause of quantum interference, non-locality, quantum entanglement and quantum discord in two-body and manybody quantum systems.The coherence of quantum states can be used to achieve challenging or impossible tasks using classical information processing methods.Therefore, the field of quantum information has received extensive attention and continued development.

3.1.Quantum metrology

Quantum metrology, utilizing quantum effects such as quantum coherence and entanglement, aims to improve the precision, efficiency and complexity reduction in the measurement and identification processes.It is a significant application area within quantum information science.Quantum metrology has many scientific and technological applications,including time and frequency detection,remote sensing,weak magnetic field detection, thermometry and optics.[85,86]Similar to quantum communication, different scenarios are possible (see Fig.3): either we do not employ quantum effects[classical–classical(CC)strategy]or quantum effects can be used only in the probe measurement [classical–quantum(CQ) strategy] or only in the probe preparation [quantum–classical (QC) strategy] or in both stages [quantum–quantum(QQ)strategy].[44]In quantum metrology,the process of measuring a physical quantity using an interferometer firstly requires the preparation of a superposition of pointer states in a quantum system.Then, it evolves under the Hamiltonian containing the measured physical quantity,and obtains the final state containing unknown parameter information.[87]However, if the pointers are unrelated to each other, the measurement precision is still limited by the shot noise limit.It was not until 1980 when Caveset al.[88]first proposed the use of photon squeezed states,when measurement precision beyond the shot noise limit was achieved in gravitational wave detection by employingNphoton squeezed states as pointer states.Currently, there is extensive theoretical and experimental research on quantum metrology methods that surpass classical limits.Quantum states such as the two-mode Fock state[89]and Schr¨odinger cat states[90]have been utilized to surpass the shot noise limit.

In general,given an initial probe stateρand assuming the probing procedure is repeatedntimes, the mean square error(∆ϕ)2in the estimation ofϕis bounded below by the quantum Cram´er–Rao bound[91]

whereI(ρ,H) is the quantum Fisher information,[92]which can be defined(under a smoothness hypothesis)as

whereFdenotes the fidelity andρt= e-iHtρeiHt.[93]The quantum Fisher information measures the sensitivity of a stateρto changes in a parametert.This parametertcharacterizes a unitary dynamics generated byH.Quantum Fisher information directly quantifies the maximum achievable precision of the estimation procedure.Therefore,it is considered to be an advantage of quantum metrology.[86]

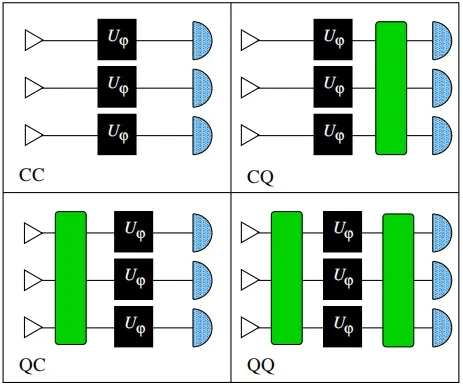
Fig.3.Different strategies for the estimation of a parameter ϕ involving N parallel samplings of a unitary operator Uϕ (black squares).The triangles on the left represent state preparation and the symbols on the right represent measurements.The green boxes represent a unitary operation involving multiple probes (Q strategies).Reproduced with permission from Ref.[44].

When using probe states without any coherence or entanglement,the quantum Fisher information can scale at most linearly withn,I(ρ,H)∼n.However,by starting with a probe stateρthat possesses coherence and applyingUϕsequentiallyntimes before the final measurement,it becomes possible to achieve the Heisenberg scaling, denoted byI(ρ,H)∼n2.This scaling leads to a genuine quantum enhancement in precision.[44]Furthermore, in the study of coherence in quantum metrology, Jooet al.[94]proposed a phase estimation scheme using entangled coherent states.Considering the limited number of particles needed to show these advantages,the optical version of entangled coherent states’metrology is achievable with current technology.Berradaet al.[95]proposed an enhanced phase estimation scheme utilizing entangled spin-coherent states (ESCSs).They showed that by increasing the spin number, the phase parameter exhibits the smallest variance compared to NOON states, both under perfect and lossy conditions.Giorda and Allegra[96]showed a relation between the statistical distance between infinitesimally close quantum states and the second order variation of the coherence of the optimal measurement basis with respect to the state of the probe.In quantum phase estimation protocols,they proposed that coherence should be considered as a resource that can optimize estimation precision.In the past,the Heisenberg limit was considered the ultimate limit achievable with quantum methods and resources.Recently,Yinet al.used indefinite causal order to achieve quantum precision measurement beyond Heisenberg’s limit precision.This experiment is of great significance for understanding the indefinite causal order and quantum precision measurement.[97]

In the practical application of quantum measurement,there are still significant challenges.These challenges primarily stem from the difficulty in preparing and controlling quantum correlation states, as well as reducing the effects of noise and ensuring the persistence of multi-particle correlations.Further research is needed to solve these problems.

3.2.Quantum channel discrimination

When one of these unitary channels acts on the probe,which is initially in a stateρ, the goal is to determine which specific channel instance has occurred.If we use any probe stateσ ∈ℐ,that is incoherent for the eigenbasis ofH,no information aboutϕis imprinted on the state.In this case, the probabilityps(σ)of correctly guessing the value ofϕis simply 1/d,which corresponds to a random guess.

However, if we prepare a probe stateρthat exhibits coherence in the eigenbasis ofH,and accompany it with an optimal measurement at the output, the probability of successps(ρ)in correctly identifying the value ofϕis greater than or equal tops(σ), whereσis an incoherent probe state.As a result,we can achieve better discrimination between the channels.These channels play significant roles in various quantum information tasks,including quantum error correction,[99]quantum cloning,[100]and dense coding.[101]These suggest a prominent role of coherence.

3.3.Witnessing quantum correlations

In recent studies, several authors have made attempts to discover Bell-type inequalities suitable for different quantifiers of coherence.Bu and Wu have developed Bell-type inequalities within the framework of quantum coherence theory,[102]specifically tailored for product states and various measures of coherence.Their findings revealed that the inequalities are violated by maximally entangled states.Moreover,they demonstrated that Bell-type inequalities based on the relative entropy of coherence are violated by all two-qubit pure entangled states,effectively serving as an entanglement witness.Building on previous results using quantum Fisher information to detect different classes of multipartite entanglement,[103–106]Girolami and Yadin further showed that coherence detection can also be used to witness multipartite entanglement.[107]

In a scenario involving two atoms moving through an external massless scalar field, Mondal and Mukhopadhyay examined the relationship between steering and quantum coherence.[109]They demonstrated that, similar to entanglement, the steering induced coherence of an equilibrium state can increase or decrease with acceleration, depending on the initial state’s conditions.Mondalet al.[110]used different coherence measures, includingl1-norm, relative entropy and skew information, to establish complementary relationships between coherences measured on a mutually unbiased basis.Using these relations,they derived conditions under which the nonlocal advantage of quantum coherence can be achieved and the state is steerable.Hu and Fan[111]investigated the maximal coherence of steered states.Asifet al.[112]have designed a classifier for detecting the separability and entanglement of quantum states, using supervised learning and Bell-type inequality for the relative entropy of coherence.

3.4.Quantum phase transitions

Employing a quantum coherence metric to investigate the quantum dynamics of many-body systems has emerged as a highly effective approach.For instance,the widely recognized nondiagonal long program in superconducting theory exhibits a direct correlation with the coherence measure based on thel1-norm.[9]Quantum entanglement has proven to be a critical tool for detecting and characterizing quantum phase transitions in various significant applications.Similarly,quantum coherence measures, as important quantitative descriptors of the quantum properties of systems,could play a similar role in analyzing such transitions.

Karpatet al.[47]and C¸akmaket al.[113]investigated the utility of skew information in analyzing quantum phase transitions.They focused on the spin-1/2 HeisenbergXYmodel in the following form:

whereσix,y,zare the usual Pauli operators at thei-th site,λdenotes the strength of the inverse field,γ ∈[0,1] is the anisotropy parameter, andNis the number of spins.They showed that single-spin coherence reliably identifies the second-order quantum phase transition in the thermal ground states.

Chenet al.[48]showed the application of coherence sensitivity in the study of quantum phase transition.Coherence sensitivity is defined as the first derivative of the relative entropy quantum coherence,

and the singularity of the coherence sensitivity, determined by the characteristic parameterλof the system Hamiltonian,proves to be a powerful tool in accurately identifying the quantum phase transition point for various models, including the transverse field Ising model,spin-1/2 HeisenbergXXmodel and Kitaev honeycomb model.Additionally,the coherence sensitivity method can pinpoint the temperature frame of quantum criticality,which perfectly coincides with experiments.

By studying quantum discord, quantum mutual information and different coherence measures, Malvezziet al.[114]investigated the quantum phase transitions and special symmetry points in spin-1 Heisenberg chains.Work on studying quantum phase transitions in other models using quantum coherence metrics can be found in Refs.[49,115].Moreover, Huet al.[116]proposed to use the steered quantum coherence as a signature of quantum phase transitions.Rossini and Vicari[117]discussed coherence and dissipative dynamics in quantum phase transitions.

4.Application of quantum coherence in interdisciplinary research

Quantum mechanics is a theory that reflects the law of motion of microscopic particles.It is the result of human indepth understanding of microscopic fields of nature and provides an important way to reveal the essence of physical phenomena.Quantum mechanics has also been applied to biology, thermodynamics and other fields, and combined to produce a number of interdisciplinary disciplines such as quantum biology and quantum thermodynamics,promoting the production of many new theories and achievements in science and technology.With the development of quantum mechanics,the role of quantum resources cannot be ignored.As a kind of quantum resource,quantum coherence plays an essential role in many systems and tasks.Obviously, quantum coherence is indispensable in interdisciplinary studies.Next, we briefly introduce the role of quantum coherence in quantum thermodynamics and quantum biology.

4.1.Quantum thermodynamics

With the development of quantum information science and quantum mechanics,some problems in statistical thermodynamics have been reconsidered.A goal of the study of quantum thermodynamics is to find a quantum heat engine with better performance than the classical heat engine by using quantum effects such as quantum coherence.The quantum heat engine is an important way for people to explore the thermodynamic properties of quantum systems.It provides an effective way for people to reveal the physical essence behind macro-thermodynamic phenomena from the micro-level, and plays an important role in promoting the establishment and improvement of the theory of quantum thermodynamics.In this section,we will mainly discuss the role of quantum coherence in quantum heat engines and quantum batteries.

4.1.1.Quantum heat engine

The concept of a quantum heat engine was first proposed in 1959.[118]Quantum simulations of the famous classical Carnot and Otto heat engines have been extensively studied[119–122]and implemented in the laboratory.[123–125]In the field of quantum information technology,quantum effects such as quantum coherence have been considered as a key quantum resource.This urges people to explore the influence of quantum effects on thermodynamic processes and whether the quantum heat engine has more advantages than the classical heat engine when it is as small as the quantum scale.Scullyet al.combined quantum coherence with thermodynamic processes creatively,and studied the effect of quantum coherence on the efficiency of a photon Carnot machine.[50]It is concluded that quantum coherence can be used as a resource to improve the efficiency of a heat engine.This greatly encouraged researchers to utilize quantum coherence to improve the efficiency of heat engines.[126–130]Moreover,quantum coherence has also been proven to be useful for transient cooling of absorption refrigerators(absorption refrigerators are refrigerators that use heat sources to provide the energy needed to drive the cooling process).[131]

In recent years, researchers have conducted extensive research on quantum coherence in quantum heat engines.[132–137]Parket al.proposed the concept of a quantum information heat engine and proved that energy can be extracted from pure quantum information.[138]Since then,this kind of heat engine has received extensive attention.[139–142]The above literature shows that quantum coherence can be regarded as a high-quality thermodynamic resource.These studies further deepen our understanding of the thermodynamic properties of quantum coherence.Although quantum resources such as quantum coherence are only one of the many factors that contribute to the quantum heat engine, we expect that with the continuous development of this field,its role will become more important.

4.1.2.Quantum battery

The quantum battery (QB) was first proposed by Alicki and Fannes,[143]and is a small quantum system that absorbs and releases energy.The quantum battery is composed of quantum systems and is expected to surpass its classical analogues.This emerging field aims to find a battery that can store energy more effectively after using quantum resources,and that is convenient for subsequent energy extraction and utilization.The quantum battery can be regarded as addimensional quantum system with nondegenerate energy levels.The charging of a quantum battery means that the quantum state changes from a low-energy state to a high-energy state.The discharge process is a reversible extraction of work from it through cyclic unitary operation.At the same time,the quantum state changes from a high-energy state to a lowenergy state.As a kind of quantum heat engine,we will have questions about whether quantum resources can promote more energy storage or faster charging and discharging of the quantum battery.Coherence is an important quantum resource,so it has always been a hot topic in the study of whether quantum resources can promote the performance of quantum batteries.Next,we will introduce the role of coherence in the quantum battery from two aspects: the extracted energy and the charge and discharge power.

Extracting energyErgotropy refers to the maximum energy that can be extracted from the charged energy in the ideal discharge process.If the battery is closed,the Hamiltonian of the battery can be written asH=Hb+Hc+λtV(t),whereHbis the free Hamiltonian of the battery,Hcis the Hamiltonian of the charger,V(t)is the interaction term of the battery and charger,andλtis a battery switch.The mathematical expression of ergotropy is

whereρbis the density operator of the quantum battery,Uis the unitary operator, andUρbU†is the density matrix of the battery in the ideal discharge final state.At present,it has been proven that the nontrivial relationship between entanglement and high performance in a quantum battery is not universal,and depends on the system that we deal with.[144]Andolinaet al.and Liuet al.proved that the entanglement between battery and charger has an adverse effect on the storage of extractable work.[145,146]So what effect does coherence have on ergotropy? Shiet al.studied the effect of quantum resources on extractable work in a quantum battery.[144]It is proved that the quantum coherence in the battery or the battery-charger entanglement ensures the generation of non-zero extractable work during the charging process.Examples of the central spin battery, Tavis–Cummings battery and spin chain battery are given to illustrate this result.On the other hand, coherence has a certain effect on the ergotropy of a quantum battery.Kaminet al.used the spin chain model to explain that coherence is a resource to improve the ergotropy of a quantum battery.[147]And it shows that entanglement is not the best resource for charging the quantum battery in all situations.When entanglement is not the best resource for charging the quantum battery, the generation of coherence is the best resource for charging the quantum battery.Considering the need for experiments,a framework called waveguide quantum electrodynamics is proposed.[148,149]This framework is usually implemented in superconducting[150]and semiconductor circuits.[151–153]Monselet al.studied the initial quantum coherence in qubits embedded in the waveguide and how the initial charge of the battery affects the work extraction.[154]It was found that the quantum coherence plays a key role in controlling energy transfer under limited energy supply.The quantum coherence of the external environment can also promote the charging performance of a quantum battery.Yuet al.proved that the quantum coherence of the bath can be used as the “fuel” of a quantum battery to improve the charging performance of the quantum battery.[155]

Charging and discharging power Power is an important parameter for measuring the charge and discharge performance.Charging power is defined as the amount of charging and discharging energy per unit time,that is,

where ∆E(t) is the charged energy of the battery at timet.Similarly, the discharge power can be defined.Zhanget al.proposed that in the ideal Dicke battery (the number of twolevel systems (TLSs)Nis far less than the number of cavity photonsn), the average charging power of a quantum battery when using the collective agreement is√Ntimes that of the parallel charging protocol.[156]It is pointed out that the source of this quantum advantage is not quantum entanglement,but is due to the coherent cooperative interactions among the TLSs.Kaminet al.used the spin chain model to explain that coherence is a resource to improve the charge and discharge power of a QB.[157]In the open system,quantum coherence can also promote the charging process of a quantum battery.Seahet al.used the collision model to describe the charging process.[158]For a battery prepared in the ground state,the unit prepared in the coherent state can charge faster than the classical unit.It is proved that the coherent protocol can generate higher charging power than any possible incoherent protocol.

4.2.Quantum biology

Quantum biology is usually regarded as a new discipline,but the origin of quantum biology can be traced back to Erwin Schr¨odinger’s famous book“What is Life?”published in 1992.[159]Some of the insights provided by these pioneering physicists are still relevant to our understanding of quantum biology today.Quantum biology uses the theory of quantum mechanics to study the process of molecular dynamic structure and energy transfer in biological processes.It is the intersection between physics,which is the basis of modern natural science, and biology, which studies extremely complex life phenomena.Studies have shown that biological phenomena such as photosynthesis, transport phenomena, bird navigation and consciousness can operate within the scope of classical physics.Some quantum features of quantum mechanics,such as coherence, can also be used in these biological phenomena.Quantum coherence and other phenomena are now widely considered to be involved in all vital processes of living cells, such as energy transfer.In this section, we will review some works on these biological phenomena.

Photosynthesis usually refers to the process through which green plants use light energy to synthesize carbon dioxide and water into organic matter, and release oxygen at the same time.Photosynthesis mainly includes two stages: light reaction and dark reaction.It involves light absorption, electron transfer, photosynthetic phosphorylation, carbon assimilation and other important reaction steps.The realization of energy conversion in nature and the maintenance of carbonoxygen balance in the atmosphere are inseparable from photosynthesis.Almost all life on earth depends on photosynthesis for energy.The energy transformation of photosynthesis can be divided into three stages.Firstly, light energy is absorbed by the light capture antenna in the form of photons.And excited electrons (excitons) are generated through the primary reaction.[160,161]Secondly, the excitons are transmitted from each antenna to the reaction center.Thirdly, active chemical energy is converted into more stable chemical energy through carbon assimilation.The precise biological structure,pigment composition,antenna and reaction center used by different organisms are different.[161,162]The light collection device of green sulfur bacteria has always been one of the models favored by researchers, as shown in Fig.5.[163]It has a chlorosome antenna that can absorb light in very weak light and then transfer the light energy captured by these chlorosomes to the reaction center through a Fenna–Matthews–Olson(FMO)complex.In the photosynthesis of a bacterium, almost every photon absorbed is successfully transferred to the reaction center, even if the intermediate electron excitation will lose energy very quickly.This shows that the energy of an exciton is transferred to the reaction center in an extremely effective way.Engelet al.provided evidence of quantum coherent energy transfer in the FMO complex.[164]In addition,they also speculated that the electron excitation may explore different transmission paths simultaneously in a coherent manner.Thus, the energy transmission efficiency is very high.Since this breakthrough, more experiments have proved that other photosynthetic systems have quantum coherence even at room temperature.[165–167]Although quantum coherence has been proved to be able to transfer energy rapidly in photosynthesis, it is not clear how quantum coherence is generated.The Hamiltonian describing the interaction between excitons and excitons is[168]

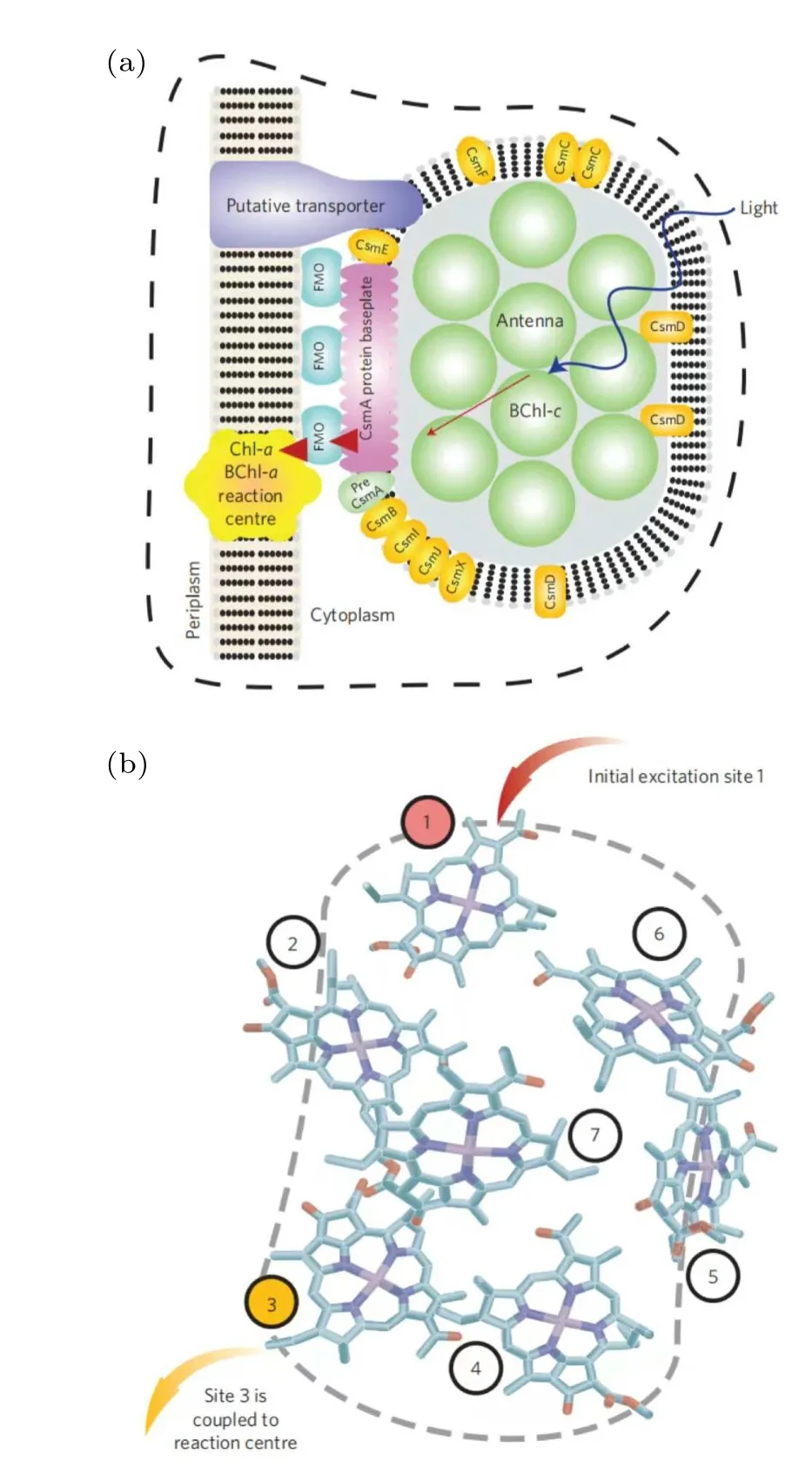
Fig.5.A quantum machine for efficient light-energy harvesting.(a)Diagram of the photosynthetic apparatus of green sulfur bacteria, including antenna, energy-conducting baseplate and FMO complexes, and reaction center.The chlorosome antenna (green discs) is composed of roughly 200000 BChl-c molecules, and is an exceptionally large structure that is designed to capture as many photons as possible in the lowlight conditions the bacteria thrive in.Sunlight creates an excitation in this antenna that is transferred(red arrows)to the reaction center through one of several FMO complexes.(b) The BChl-a arrangements of one of the FMO pigment-protein complexes through x-ray diffraction.The FMO complex comprises eight (although only seven are shown here)bacteriochlorophyll-a (BChl-a) molecules that are encased in a protein scaffolding (not shown).The excitation arrives from the chlorosome at one of the sites, typically thought to be the site denoted by 1.This excitation is then transported from one BChl molecule to the next.Once it arrives at site 3 it can irreversibly enter the reaction center and start a charge-separation process.Reproduced with permission from Ref.[163].

It was found that the coherent part of the equation is not enough to explain the high efficiency of energy transfer.New studies[169–173]found that the interaction between an exciton and a protein vibration mode led to the quantum coherence of these photosynthetic systems at room temperature.In addition, it is also recognized that quantum coherence plays an important role in the transport process.[174,175]

Quantum coherence not only plays an important role in photosynthesis and transport phenomena,but it has also been speculated that there is a link between quantum coherence and consciousness.[176,177]Unfortunately, the proposed model is also controversial.Even if decoherence exists in nature, the time required for decoherence is much earlier than the physiological time scale and so it is not possible for coherence to work on the physiological time scale.[178,179]In addition, the magnetic induction of birds is also speculated to be closely related to quantum coherence.[54,180–182]Although there are disputes, the experimental efforts to prove or refute these ideas will bring new ideas and insights into the role of quantum coherence in life science and also effectively promote the development of quantum biology.

5.Conclusion

Quantum coherence originates from the superposition of quantum states.It is a fundamental concept in quantum theory.It also plays an important role in emerging fields such as quantum information.Studying the various properties of quantum coherence in depth not only enables people to better understand this basic physical concept, but can also promote the development of related fields.First, we review the basic framework of quantum coherent resource theory,including the definition of an incoherent state and the basic conditions that a quantum coherence metric function needs to meet.In addition, we also review the relationship between quantum coherence and other quantum resources and the dynamic evolution of quantum coherence in open systems.In this paper,we mainly reviewed the typical applications of quantum coherence in quantum computing, quantum information and quantum interdisciplinary research.

Compared with classical computers, studying quantum computing and quantum information can better speed-up classical computing,and it can greatly improve the computational efficiency of existing classical computers.This is precisely because quantum computing mainly involves parallel computing,and the core of parallel computing is quantum coherence.Therefore, studying the specific changes of quantum coherence under quantum algorithms plays an important role in the development of quantum computing.In this paper, we introduce the role of coherence in quantum computation.Firstly,we introduce the role of quantum coherence in the Deutsch–Jozsa algorithm, Grover algorithm, DQC1 and quantum random walk search algorithm respectively.In the above algorithms,quantum coherence is a resource that plays a key role.For the Deutsch–Jozsa algorithm,quantum coherence can increase the probability of correct decision-making.For the Grover algorithm,the search success probability is linearly related to the quantum coherent depletion, which indicates that the more coherence that is consumed, the higher the probability of success.For DQC1, the accuracy of outcome can be quantified in terms of the recoverable coherence,which indicates that the more coherence that is consumed, the higher the accuracy of output results.Meanwhile, a similar conclusion is drawn in the quantum walk search algorithm that the search algorithm cannot be executed using a state without coherence.Secondly,we introduce the problem of decoherence in superconducting qubits and briefly summarize the previous research.Thirdly, we give a brief review of quantum simulation and discuss the progress of quantum simulation using atoms in optical lattices,photons and superconducting circuits.Although there have been extensive and in-depth research results,the research in the field of quantum coherence is still full of vitality,and many interesting and challenging problems still need to be solved in the future.The research into quantum coherence has become an important research topic and direction in the field of quantum computing.Moreover, as well as the result above,the behaviors of quantum coherence under other quantum algorithms and other metric measures also have great research value, which may lead to more general results.The application of coherence in engineering also needs further research.Since this field has enormous application potential, it will develop further in the coming years.

Quantum information science is a multidisciplinary field combining quantum mechanics and information science.Compared with traditional information technology, quantum information science not only shows unparalleled advantages,but also provides a revolutionary direction for development.In addition, the development of quantum information science has also promoted the refinement of quantum theory and deepened the understanding of the basic essence of quantum mechanics.In this paper,the importance of coherence in quantum metrology,quantum channel discrimination,witnessing quantum correlations and quantum phase transition is introduced.This paper also briefly introduces the role of quantum coherence in quantum thermodynamics and quantum biology.But coherence does more than that.We expect that a large amount of future research will focus on all aspects of the overlapping fields of physics, information theory, biology and other branches of science and engineering.

Acknowledgments

Project supported by the National Natural Science Foundation of China(Grant No.12175179),the Peng Huaiwu Center for Fundamental Theory (Grant No.12247103), and the Natural Science Basic Research Program of Shaanxi Province(Grant Nos.2021JCW-19 and 2019JQ-863).