In-plane spin excitation of skyrmion bags
Shuang Li(李爽), Ke-Xin Li(李可欣), Zhao-Hua Liu(刘照华), Qi-Yuan Zhu(朱起源),Chen-Bo Zhao(赵晨博), Hu Zhang(张虎), Xing-Qiang Shi(石兴强),Jiang-Long Wang(王江龙), Rui-Ning Wang(王瑞宁), Ru-Qian Lian(连如乾),Peng-Lai Gong(巩朋来), and Chen-Dong Jin(金晨东),†
1Key Laboratory of Optic-Electronic Information and Materials of Hebei Province,Research Center for Computational Physics,College of Physics Science and Technology,Hebei University,Baoding 071002,China
2College of Mathematics and Physics,Chongqing University of Science and Technology,Chongqing 401331,China
3Department of Materials Science and Engineering,Lanzhou University of Technology,Lanzhou 730050,China
Keywords: skyrmion bags,spin-wave mode,power spectral density,micromagnetic simulation
1.Introduction
Magnetic skyrmions, as topologically protected spin structures characterized by topological charges, have been widely studied in recent years.[1–17]Skyrmions have the characteristics of small size,topological protection,and low drive current density,which are conducive to the technical applications in high-density data storage equipment and low-energyconsumption spintronic devices.[18–22]In particular, the theoretical application of skyrmions has been extended to antiferromagnetic skyrmions,including racetrack memories,logic devices,spin nano-oscillators,and other promising spintronic devices derived from no spin Hall effect,zero stray field,and ultra-fast magnetization dynamics.[23–25]Recently, the interaction between spin wave and skyrmion has attracted considerable attention.[26–35]The propagating spin wave strongly depends on the excitation mode of a skyrmion in frequency,decay length, and group velocity.[33]The spin excitation of microwave AC magnetic field has attracted a lot of attention due to its potential application in the design of spin-wave devices.[27,35–41]As is well known, the spin-wave mode of skyrmion contains in-plane counterclockwise(CCW)rotation mode and clockwise (CW) rotation mode, and one out-ofplane breathing mode.[27,36]In addition,the spin-wave modes of 2πskyrmion,[37,38]elliptical skyrmion,[41]bimeron,[42]magnetic hopfion of three-dimensional(3D)space,[39]and 3D skyrmions lattice[43]have been studied.For example,the spinwave mode of 2πskyrmions contains four in-plane modes including two CW modes, two CCW rotation modes, and two out-of-plane breathing modes;[37,38]the simple breathing mode of elliptical skyrmion splits into two complex breathing modes owing to the breaking of the rotational symmetry of the spin texture;[41]the spin-wave mode of bimeron presents an anisotropic property when the microwave magnetic field is applied in the plane;[42]the spin-wave mode of magnetic hopfion contains five modes of breathing and rotating characters;[39]the spin-wave mode of the 3D skyrmion lattice exhibits the CCW mode and CW mode that are excited in pair as the film thickness increases in the in-plane;[43]three coupled excitation modes were found in the antiferromagnetic exchange coupling disk.[44]
Skyrmion bags are spin structures with arbitrary topological charges, each of which is composed of several small skyrmions with opposite topological charges inside a larger skyrmion.[45–48]Compared with skyrmions, skyrmion bags have high topological charges to represent more information.[49,50]Skyrmion bags were discovered in the liquid crystal and the thin plate of B20 chiral FeGe magnet by polarized optical microscopy and Lorentz transmission electron microscopy, respectively.[46,51,52]By numerical simulations, the interaction of stable skyrmion bags in the liquid crystal is similar to that of large skyrmions.[46]Moreover,the stability and current-induced motions of skyrmion bags have been investigated by micromagnetic simulations and in experiment,[46,48,51,53–55]the spintronic devices with tunable magnetic fields and variable topological charge driven by current have important application prospects.[46,48,51,53,54,56]Up to now, the in-plane spin excitation modes of skyrmion bags are still unclear.The in-plane spin excitations of skyrmion bags should be richer than those of skyrmions,because of the nested structure.Therefore,to manipulate skyrmion bags and promote the development of their potential applications, it is particularly important to study the spin excitation of skyrmion bags by applying an in-plane microwave magnetic field.In this work,we first calculate the ground state of the skyrmion bags,including the total topological charge and the total energy.Then, we calculate the power spectrum of the skyrmion bags and the corresponding spin-wave mode.Finally,we study the time evolution of skyrmion bag excitation, which contributes to a better understanding of each spin-wave mode.
2.Micromagnetic simulation details
The ground state and spin-wave resonance modes of skyrmion bags are obtained by solving the Landau–Lifshitz–Gilbert (LLG) equation with object oriented micromagnetic framework (OOMMF).[57]The LLG equation can be expressed as follows:
wheremis the unit vector of magnetization,αis the Gilbert damping parameter and is set to 0.5 and 0.01 for the solution of the ground state and the resonant excitation procedure,respectively,Heffis the total effective field composed of the Heisenberg exchange field, the Dzyaloshinskii–Moriya interaction(DMI)field,the uniaxial anisotropy field,the demagnetization field,and the applied field.The applied field is set toBx(t)=B0sinc(2π ft) andBx(t)=Bxsin(2π ft) for the excitation spectrum solution and the time evolution solution,respectively.The simulation radius of the nanodisk is 100 nm and the cell size is 1 nm×1 nm×0.4 nm.Typical parameters for Co on heavy metal substrate parameters are cited from Refs.[21,54,58],exchange constantA=1.5×10-11J/m,DMI constantD= 3.5×103J/m2, uniaxial anisotropy constantKu=0.8×106J/m3,and saturation magnetizationMs=5.8×105A/m.Such parameters guarantee the existence of different types of skyrmion bags,as reported in Refs.[40,53,54,59].The ground state of skyrmion bag is denoted by S(n), wherenrepresents the number of inner skyrmions.The definition of skyrmion bag in this work is similar to that in Ref.[46], so the skyrmion bag shown in Fig.1(a)is denoted as S(4).Owing to the boundary potential and the large enough interfacial DMI,the initial position of the outer skyrmion(the polarity is+1)is stable in the middle of the nanodisk,and the four inner skyrmions (the polarity is-1) are centrally symmetric.The skyrmion bags are described by topological chargeQ,[3,60]
whereQis the total topological charge.Figure 1(b) shows the topological density distribution corresponding to S(4).The topological density of the outer skyrmion boundary region reaches to 4.2×1015m-2, and the topological density of the four inner skyrmions’ region has the lowest value of-2.44×1015m-2.By integrating the topological density of the entire nanodisk, the topological charge of S(4) is-3.It should be noted that if the background magnetization direction is reversed,then the topological charge sign of skyrmion bags will be reversed correspondingly.
3.Results and discussion
3.1.Ground state, total topological charge and total energy of S(0)–S(9)
We first calculate the ground state of S(0)–S(9)in Fig.2 by micromagnetic simulation.To obtain the ground state of skyrmion bag, we place a large bubble into the nanodisk and then set small bubbles into the large bubble.Then, we relax the magnetic system and obtain the minimum value of the total energy by using a conjugate gradient method implemented in the OOMMF code.[57]The magnetic system is considered stable when the change of the measured total energy is less than 1/105in 10 ns.[53]The arrows point in thez-direction away from the center of the skyrmion, and an elementary full skyrmion(S(0))has a topological charge-1 as shown in Fig.2(a).Inside a stretched skyrmion,the arrows point in the-zdirection,and a skyrmion placed here hasQ+1,so the 2πskyrmion(S(1))has a topological charge as shown in Fig.2(b).Furthermore,asn>1,S(n)represents different skyrmion bags shown in Figs.2(c)–2(j), and their stabilities have been systematically analyzed in thin magnetic films by simulations.[53]The magnetic moment direction of the ground state of S(0)–S(9) are shown in Fig.2.Skyrmion bag is a nested structure of small skyrmions contained by a big skyrmion, and its size becomes larger due to the increasing number of skyrmions.In addition,to further investigate the properties of skyrmion bag,we calculate the functional relationship between the total topological charge(Q)and S(n),and that between the total energy(E)and S(n).
Figure 3(a)shows thatQdecreases from 1 to 8 withnincreasing from 0 to 9,soQ=1-n.Figure 3(b)shows thatEincreases from 2.448×10-18J(S(0))to 3.277×10-18J(S(9))with the increases of S(n),which means that the stability of the skyrmion bags decreases as the number of inner skyrmions increases.

3.2.Map of power spectral density of skyrmion bags
To investigate the spin excitation of skyrmion bags, the power spectral density (PSD) of skyrmion bag is calculated as shown in Fig.4.Specifically, we study the map of PSD of skyrmion bags varying withnto compare the differences among the different modes of skyrmion bags.For the excitation spectrum of each skyrmion bag,the map of PSD indicates the number of resonance frequencies as well as the linewidth of each resonant frequency,the magnitude of the peak amplitude is represented by the color depth of the color code.The excitation pulse is the sinc functionBx(t) =B0sinc(2π ft),where the amplitudeB0is 10 mT in thex-axis direction as shown in Fig.4(a).The cutoff frequency is set to 50 GHz.The excitation frequency can be obtained by the fast Fourier transform (FFT) of the oscillation of the in-planexcomponent of magnetization, and then the PSD phase diagram of skyrmion bags with S(n) is obtained by changing S(n) as shown in Fig.4(b).In earlier work, for S(0) as a single skyrmion, the number of in-plane excitation modes depends on the DMI value;[41]the in-plane excitation mode of 2πskyrmion S(1) exhibits two resonance modes, and the relationship between the resonant mode and the uniform magnetic field is studied.[37]We mainly focus on the excitation spectrum of skyrmion bag, i.e., S(n)>1, there are four inplane resonance modes of skyrmion bags,which are different from those of skyrmions and 2πskyrmions.The resonance frequency of mode 1 increases monotonically with S(n) increasing from 0.7 GHz (S(2)) to 4.9 GHz (S(9)).With S(n)increasing from S(2)to S(9),the resonance frequency of mode 2 and mode 4 remain unchanged at 10 GHz and 45 GHz,respectively.The resonance frequency of mode 3 decreases from 16.3 GHz (S(1)) to 14.5 GHz (S(3)) and then increases to 22.9 GHz(S(9)).It is found that the number of modes of the skyrmion bag does not change withnwhenn>2,but the resonance frequencies of different modes shift withn.Because each skyrmion bag has four specific modes excited by the inplane microwave magnetic field,these modes may be used for detecting and characterizing skyrmion bags.

3.3.In-plane spin-wave modes of skyrmion bags
Taking the S(4)-type skyrmion bag for example,the spinwave modes of skyrmion bags at in-plane resonance frequencies are studied in detail, as shown in Fig.5, the four inplane resonance frequencies of S(4) are 2.2 GHz, 9.6 GHz,15.4 GHz,and 44.3 GHz,respectively.For mode 1 at 2.2 GHz,the resonance amplitude ofδmzin the in-plane magnetization region of the outer skyrmion and inner skyrmion are both larger.The phase of the spatial distribution of the outer skyrmion changes continuously from-πtoπ, and the phase changes of the four inner skyrmions are opposite to that of the outer skyrmion.For mode 2 at 9.6 GHz, the spatial distribution of the resonance amplitude of the outer skyrmion is larger than those of four inner skyrmions.The phase of the outer skyrmion region changes continuously fromπto-π,and the phase difference in phase among the four inner skyrmions isπ/2.For mode 3 at 15.4 GHz,the resonance distribution and phase variation are similar to those for mode 2,and the difference is that the resonance amplitude of the inner skyrmions is larger than that of the outer skyrmion.For mode 4 at 44.3 GHz,the spatial distribution of the resonance amplitudes is concentrated in the region of the inner skyrmions, and the phases of the four inner skyrmions all vary fromπto-π.
3.4.Compound modes of rotation and breathing of skyrmion bags under in-plane microwave magnetic field
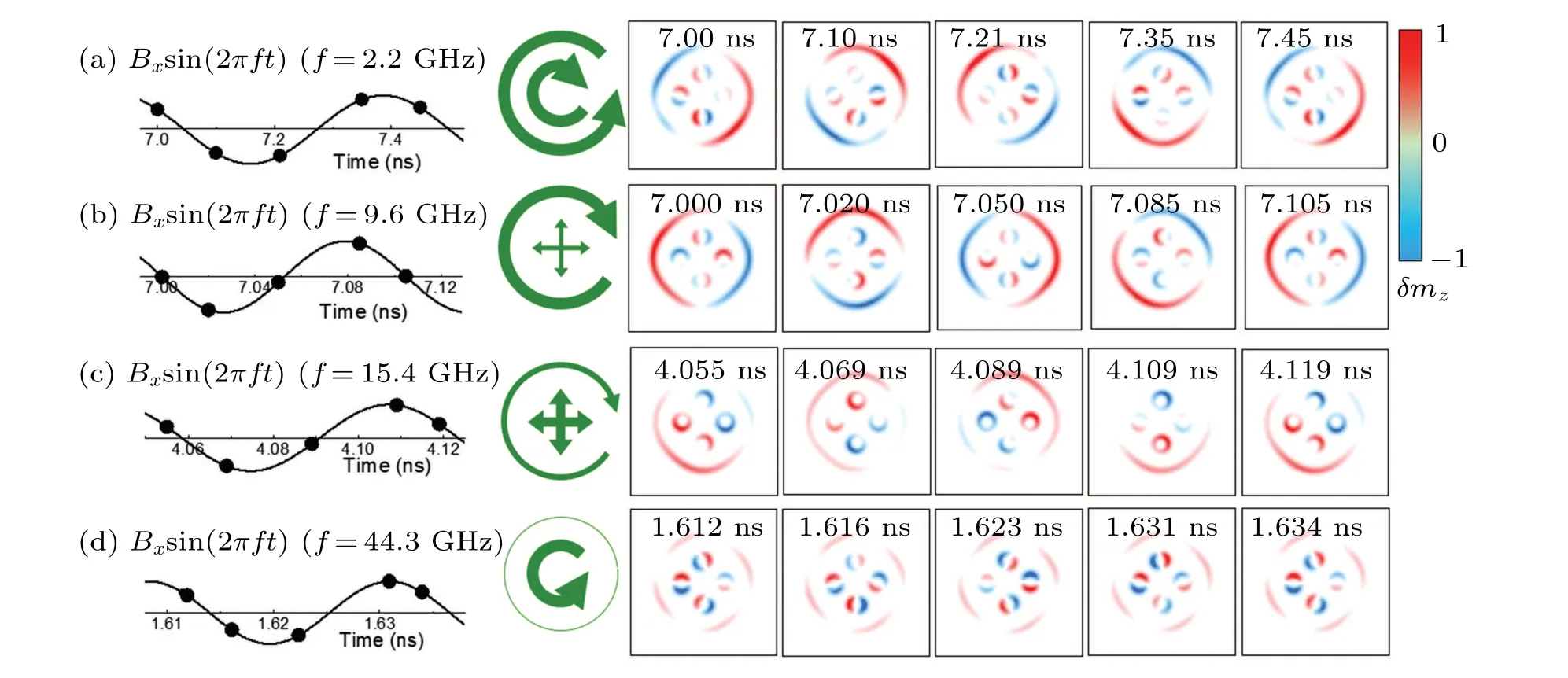
To further identify each spin-wave mode shown in Fig.5,we investigate the magnetization component of the skyrmion bags at different times by applying a sine-function magnetic fields with different resonance frequencies, to the bags as shown in Fig.6.The sine-function microwave magnetic field is expressed asBx(t)=Bxsin(2π ft),whereBx=10 mT,fis the resonance frequency of each spin-wave mode.To observe the changes of the skyrmion bag under the action of the sinefunction microwave magnetic field, we present the snapshots ofδmz(t)at different times,whereδmz(t)is the difference between thez-direction magnetization component changing with time and thez-direction magnetization component of the initial state,and it can be expressed asδmz(t)=mz(t)-mz(0),whereδmz(t)is normalized to observe its variation more clearly.The time evolution of the skyrmion bag in a circle is shown in five snapshots in Fig.6(a) when an in-plane microwave AC magnetic field at 2.2 GHz is applied to the skyrmion bags.The outer skyrmion and the inner skyrmion exhibit the CCW rotation mode and the CW rotation mode, respectively.The opposite directions of the inner rotation and the outer rotation result from the opposite directions of the opposite polarity of the inner skyrmions and the outer skyrmion.The CW modes of the inner skyrmions are not seen to be in phase,resulting from the rotation symmetry of the inner skyrmions being broken due to the influence of the CCW mode of the outer skyrmion.Figure 6(b) shows the spin-wave modes at 9.6 GHz: the outer skyrmion shows the CW rotation mode,and the weak breathing mode of the inner skyrmions traces the CW rotation mode of the outer skyrmion.Figure 6(c)shows the spin-wave modes at 15.4 GHz, i.e., the weak CW rotation mode of the outer skyrmion and the strong breathing mode of the inner skyrmions following the CW rotation mode of the outer skyrmion.For the spin-wave modes at 9.6 GHz and 15.4 GHz, the outer skyrmion shows the same CW rotation mode as a single skyrmion with the increase in frequency;the inner skyrmions do not show the CCW mode but a breathing mode following the CW mode of the outer skyrmion, because the rotation symmetry of the skyrmion bag is broken with the increase in frequency.The supplementary material video shows the time evolutions ofmzandδmzat various resonance frequencies, which can conduce to the understanding of the in-plane spin-wave modes of skyrmion bags,whereδmzis normalized.As can be seen from videos 2 and 3, the inner skyrmion of mode 2 with the largest distance from the outer domain wall is always the largest; mode 3 is a similar mode, with the key difference being that the inner skyrmion with the largest distance from the outer domain wall is always the smallest.The higher frequency of mode 3 causes the breathing of inner skyrmions to fail to keep up with the rotation change of the outer skyrmion.Figure 6(d)shows the spin-wave modes of the skyrmion bag at 44.3 GHz, in which the outer skyrmion has almost no resonance, and the inner skyrmion shows a CCW rotation mode.It can be seen from video 4 that the CCW modes of the four inner skyrmions are in phase without the influence of the domain wall of the outer skyrmion.
The above results provide a method to manipulate the dynamics of skyrmion bags in nanostructures by using a microwave magnetic field.For example, in the future, it will be possible to create,[61]drive[62]or even detect and characterize the skyrmion bags[63]by using microwave magnetic fields, which is similar to the reported method of operating skyrmions.In addition, the in-plane spin-wave modes of skyrmion bags include some new rotation-breathing coupling modes (the breathing mode generally appears in the out-ofplane excitation of the skyrmion[40]), which can be used for realizing the logic devices and also contribute to the development of skyrmion bags-based oscillators.
4.Conclusions
In summary, we first investigated the ground state of skyrmion bag.We showed that the energy of geometrically confined skyrmion bags follows the same nearly linear dependence on topological charge as that of an extended system.By studying the in-plane excitation of skyrmion bags, we found that the skyrmion bags have four complex main spin-wave modes,which are different from the simple rotation modes of skyrmions.In addition, we focused our attention on the spin excitation of skyrmion bags.With the increase of resonance frequency,the four in-plane resonance modes are found as follows: for mode 1, the outer skyrmion is in a strong CCW rotation mode and each inner skyrmion is in a strong resonance CW rotation mode; for mode 2, the outer skyrmion is in a strong CW rotation mode and the inner skyrmions are of weak breathing mode; for mode 3, the outer skyrmion is in a weak CW rotation mode and inner skyrmions are of strong breathing mode; for mode 4, the outer skyrmion almost has no resonance and each inner skyrmion is in a strong CCW rotation mode.Because the skyrmion bags possess nested structures of skyrmions,they have some more complex in-plane spin-wave modes than a single skyrmion.Our results conduce to the understanding of the in-plane spin-wave modes of skyrmion bags and may provide a reference for designing the spintronic and logic devices.
Supplementary material
For more information about the micromagnetic simulation,readers may refer to the time domain variation videos ofmzandδmzat each resonance frequency in the supplementary material,videos 1–4 corresponding to modes 1–4 in sequence.
Acknowledgements
Project supported by the National Natural Science Foundation of China (Grant Nos.12104124 and 12274111),the Natural Science Foundation of Hebei Province, China(Grant Nos.A2021201001 and A2021201008), the Central Guidance Fund on the Local Science and Technology Development of Hebei Province, China (Grant No.236Z0601G),the Post-graduate’s Innovation Fund Project of Hebei Province, China (Grant No.CXZZSS2023007), the Advanced Talents Incubation Program of the Hebei University, China (Grant Nos.521000981395, 521000981423,521000981394,and 521000981390),the Research Foundation of Chongqing University of Science and technology, China(Grant No.ckrc2019017),and the High-Performance Computing Center of Hebei University,China.
- Chinese Physics B的其它文章
- Optimal zero-crossing group selection method of the absolute gravimeter based on improved auto-regressive moving average model
- Deterministic remote preparation of multi-qubit equatorial states through dissipative channels
- Direct measurement of nonlocal quantum states without approximation
- Fast and perfect state transfer in superconducting circuit with tunable coupler
- A discrete Boltzmann model with symmetric velocity discretization for compressible flow
- Dynamic modelling and chaos control for a thin plate oscillator using Bubnov–Galerkin integral method

