Effect of short-term plasticity on working memory

Fan Yang(杨帆) and Feng Liu(刘锋)

Department of Physics and Institute for Brain Sciences,Nanjing University,Nanjing 210093,China

Keywords: bump attractor,synaptic plasticity,robustness,sensitivity

1.Introduction

Working memory (WM) refers to the brain function of holding and manipulating information over short time periods and is involved in diverse cognitive behaviors such as reasoning, decision making and learning.[1–4]Oculomotor delayed response(ODR)task is a classical experimental paradigm for working memory, where an animal is trained to saccade in the direction indicated by a cue presented seconds earlier.[5,6]During the interval between cue removal and action initiation,i.e.the delay period,selective neurons in the dorsolateral prefrontal cortex (PFC) exhibit elevated spiking activity.It has been proposed that this persistent firing underlies spatial working memory.[5,7]

The self-sustained activity in a recurrent neural network is often manifested as a bump attractor, arising from the interplay between local excitation and global inhibition.[7]Typically, the interaction between activated pyramidal cells, mediated by NMDA receptors, forms a self-reinforcing mechanism characterized by slow dynamics, enabling the sustained firing of these cells.Simultaneously,the inhibition exerted by interneurons through GABA receptors ensures global control and facilitates a winner-takes-all mechanism within the network.

Notably, synaptic plasticity, particularly short-term plasticity(STP),is also recognized as playing a role in the maintenance of WM.For example, short-term facilitation(STF)enhances the ability of a neural circuit to sustain persistent activity following a transient stimulus.[8]The slow dynamics of STP allow tuning the tradeoff between accuracy and flexibility in a WM circuit.[9]Interestingly, STP has been implicated in memory biases resulting from the previous experiment[10,11]and supports an activity-silent mechanism of WM.[12]Thus,although persistent firing is widely accepted as the substrate of WM,the influence of STP on WM cannot be overlooked.

It was reported that STF has a stabilizing effect on WM,in contrast to short-term depression (STD) in a firing rate based model.[13]However,the impact of STP on cue detection sensitivity and memory storage against distraction remains unclear.To this end,we built a spiking neural network to examine the mechanisms underlying WM in the ODR task.Our analysis dissects the contributions of STF and STD to the stability of memory storage and the network’s sensitivity to cue presentation.This study indicates that appropriate levels of STP are required to ensure robust memory maintenance.

2.Methods

2.1.Network model

To recapitulate the mnemonic behavior on the ODR task,we constructed a recurrent network model in a manner similar to that in Ref.[7].The network consists of 2048 pyramidal cells (E) and 512 interneurons (I) [Fig.1].All neurons are labeled by their preferred directions, which are uniformly distributed between 0◦and 360◦.Neurons are recurrently connected;the connections between pyramidal cells are structured,while the others are uniform.

Both pyramidal cells and interneurons are described by the leaky integrate-and-fire (LIF) model.The membrane potentialVm(t)of each neuron obeys

whereCm,gLandVLdenote the membrane capacitance,leaky conductance and resting potential, respectively.Irecis the total amount of recurrent currents in the network, andIbgdenotes the random background inputs from neurons outside the network.During a specific time period, only a subset of pyramidal cells receives a stimulusIstim, representing a cue-or distractor-related input.The neuron generates a spike whenever its membrane potential reaches a thresholdVth,followed by a reset toVresduring a refractory period (τref).For pyramidal cells,Cm= 0.5 nF,gL= 25 nS,VL=-70 mV,Vth=-50 mV,Vres=-60 mV andτref=2 ms;for interneurons,Cm=0.2 nF,gL=20 nS,VL=-70 mV,Vth=-50 mV,Vres=-60 mV andτref= 1 ms.The ordinary differential equations were integrated using a second-order Runge–Kutta algorithm,with a time step of 0.1 ms.d

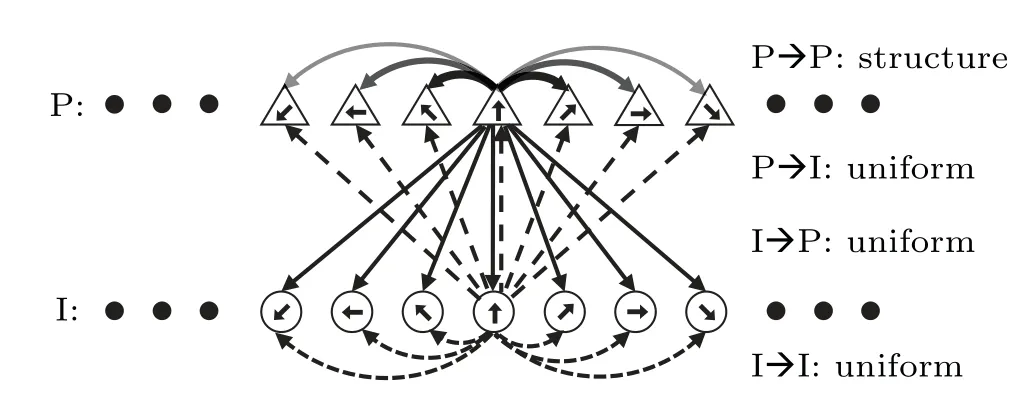
Fig.1.Schematic of the ring attractor network model.Pyramidal cells and interneurons are uniformly distributed on a separate ring,with their preferred directions indicated by labeled short arrows.Pyramidal cells with more similar preferred directions have stronger connectivity strength,as reflected by the depth of the arrows.

The inputIstimis modeled as an injected current to pyramidal cells:Istim(θ)=I0exp[-(θ-θs)2/2σ2s], whereθslabels the direction of a cue or distractor, andσsrepresents its width and is always set to 18◦.θsvaries in different situations,andI0=500 pA unless otherwise specified.In simulation,the cue always appears at 75 ms and lasts 250 ms;on some trials,the distractor appears at 375 ms,with the same strength,width and duration as the cue but at a distinct position.

Different from the stimulus input, both recurrent currents and background inputs are transmitted by synapses.Excitatory postsynaptic currents (EPSCs) are mediated by NMDA receptors (NMDARs) and AMPA ones (AMPARs),while inhibitory currents are mediated by GABAAreceptors(GABARs).Considering that NMDAR-mediated recurrent currents have proved indispensable for sustained activity in working memory,[14,15]here recurrent excitatory currents are purely NMDAR-driven for simplicity,and background synaptic currents are solely AMPAR-controlled,as in Ref.[7].

For neuroni,Irec=Ii,NMDA+Ii,GABAandIbg=Ii,AMPA,with

whereViis the membrane potential,VE= 0 mV andVI=-70 mV are reversal potentials for excitatory and inhibitory synapses, respectively.The extracellular magnesium concentration ([Mg2+]) is set to 1 mM.[16]gjilabels the maximum synaptic conductance from neuronjto neuroni,depending on ion channels and cell pairs.sjdenotes the gating variable.pjrepresents the synaptic efficacy with short-term plasticity, as will be described in Subsection 2.2.

Given a spike train{tk}in the presynaptic neuronj, the gating variablessj,AMPAandsj,GABAfollow the first-order dynamics:[7]

withτNMDA=100 ms,αNMDA=0.5 kHz,andτx=2 ms.

The strength of recurrent connectivity between neurons simply depends on the difference between their preferred directions:Wij=W(θi-θj);correspondingly,gij=WijG,withGE→E=1.09 nS,GE→I=0.846 nS,GI→E=1.336 nS andGI→I=1.024 nS.W(θi–θj)is normalized,obeying

The background activity is modeled as an independent Poisson spike train with a frequency of 1.8 kHz (given 1000 presynaptic neurons, then each neuron fires independently at 1.8 Hz).The corresponding synaptic conductance (Gext) is 3.1 nS and 2.38 ns for pyramidal cells and interneurons, respectively.

2.2.Short-term plasticity

The short-term plasticity is modeled based on the synaptic efficacy adaptation at pre-synapses.[12]Letube the current release probability of neurotransmitters andvbe the fraction of resources available for depletion; the instantaneous synaptic efficacy is thus depicted byp=uv.When a spike occurs,the release probability increases due to the flux of calcium into the axon terminal,which acts as a mechanism of short-term facilitation.Meanwhile,a portion of the remaining resources is utilized for chemical transmission, causingvto decrease and function as the short-term depression component.Between spikes,udecays over time with a timescale ofτF,while the replenishment of neurotransmitters occurs with a time constant ofτD.Overall, the dynamics of STP can be described as follows:

wheretspdenotes the spike timing,andU(0

2.3.Population firing profile

The population firing profile (PFP) during the delay period is often used to characterize the overall state of the network,involving the firing rates of all pyramidal cells over each bin of 10 ms.[18]Worthy of attention are its heightHPFPand sharpnessSPFP.HPFPlabels the difference in firing rate between the neurons whose preferred directions are around the cue direction and those whose directions are opposite the cue direction,i.e.,

SPFPresembles the kurtosis describing probability density functions and is defined as

wherefiandθiare the firing rate and preferred direction of celli, andθcis the cue direction.SPFPis equal to 1.8 for the plateau-like profile and 3.0 for the standard Gaussian curve.

To track the memory state in the network,a population activity vectorPis used to infer the peak location of the bump attractor during a given time interval,

whereFiis a vector,with directionθiand amplitude representing the average firing rate of neuroniduring the 500 ms bin centered on timet.The angle ofP,θP,represents the remembered cue direction,subject to drifts caused by the randomness of background inputs.The length ofP,LP,somewhat reflects the strength of memory storage.

3.Results

3.1.Short-term plasticity at single synapses

To clarify the impact of STP on WM,we first investigated the synaptic plasticity at single synapses.For fixedU(=0.2),the synaptic plasticity is modulated byτF,τDand the firing ratefof the presynaptic neuron.Given that the synaptic efficacyp=uvis equal toUat the resting state,the synapse exhibits facilitation forp>Uand otherwise depression.When the neuron periodically discharges at 3 Hz,uandvundergo a series of pulses;with each spike,uincreases instantly and then declines gradually, whilevdisplays the opposite pattern [Fig.2(a)].After seven spikes,uandvvary periodically,and thusposcillates between 0.34 and 0.49.Overall,this represents synaptic facilitation.However, when the firing rate reaches 30 Hz,uandvchange periodically after only eight spikes(much earlier in time),andpfluctuates between 0.12 and 0.24[Fig.2(b)];in this case,the synapse demonstrates overall depression.

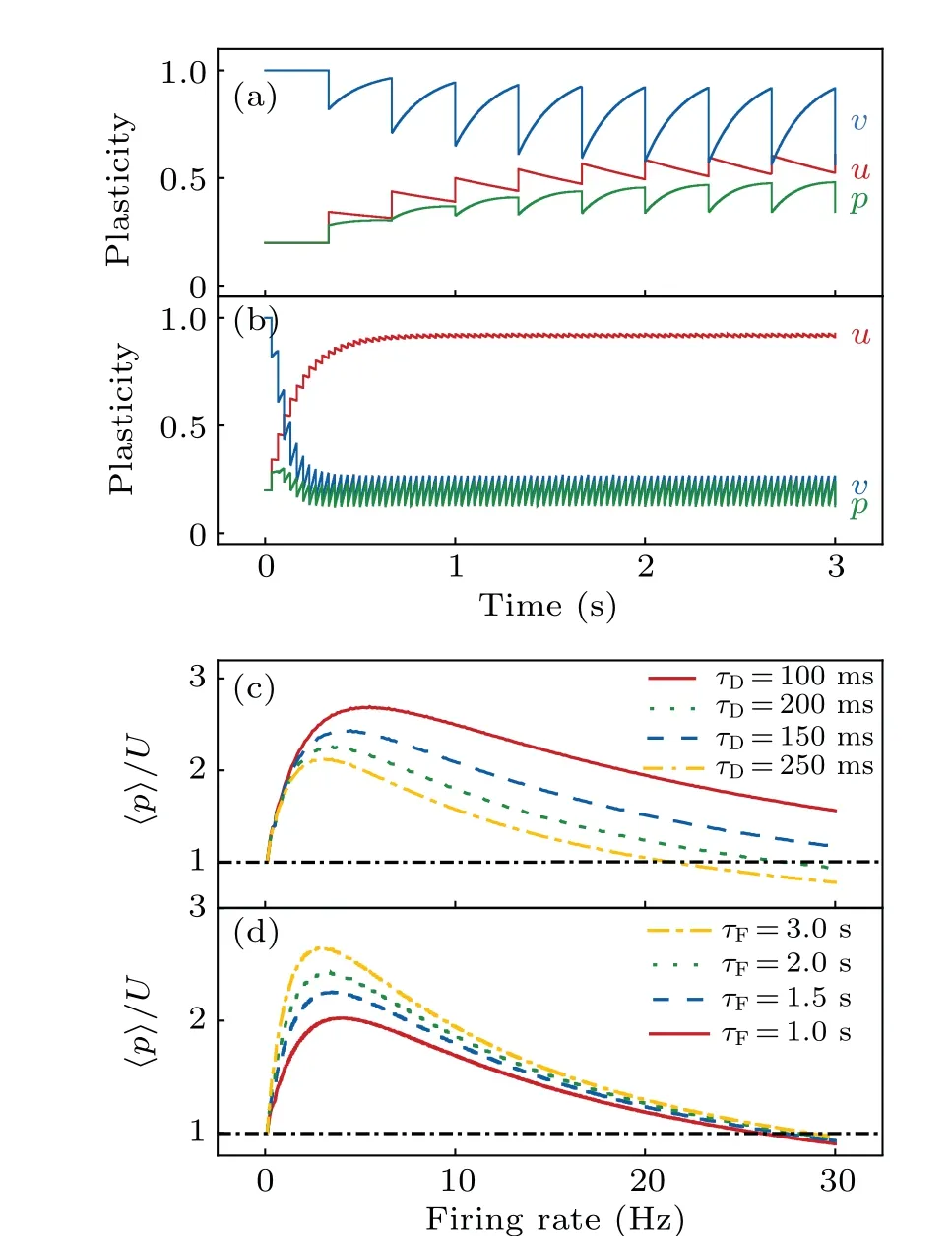
Fig.2.Strength of synaptic plasticity under various conditions.(a)and(b)Time courses of u(pink),v(blue)and p(green)with τD=200 ms,τF=1.5 s and the firing rate of 3 Hz(a)or 30 Hz(b).(c)Time-averaged p/U as a function of firing rate for different τD values,with τF fixed at 1.5 s.The synapse shows facilitation if the ratio is greater than one.(d)Time-averaged p/U as a function of firing rate for various τF values with τD=200 ms.

To further reveal the dependence of synaptic efficacy onf,τFandτD, we calculated the average ofpover one full period,〈p〉.It first increases and then decreases with increasingfat fixedτFandτD; the peak shifts rightwards and its height elevates with decreasingτD[Fig.2(c)].In contrast,the peak shifts leftwards and becomes higher with increasingτF[Fig.2(d)].Note that〈p〉>Uoccurs over a relatively wide range off, which is more prominent at largerτFand smallerτD.Together,givenτF≫τD,synaptic facilitation can be achieved when the firing rate is not high; increasingτFor decreasingτDalways enhances the synaptic facilitation.

3.2.Maintenance of working memory with STP

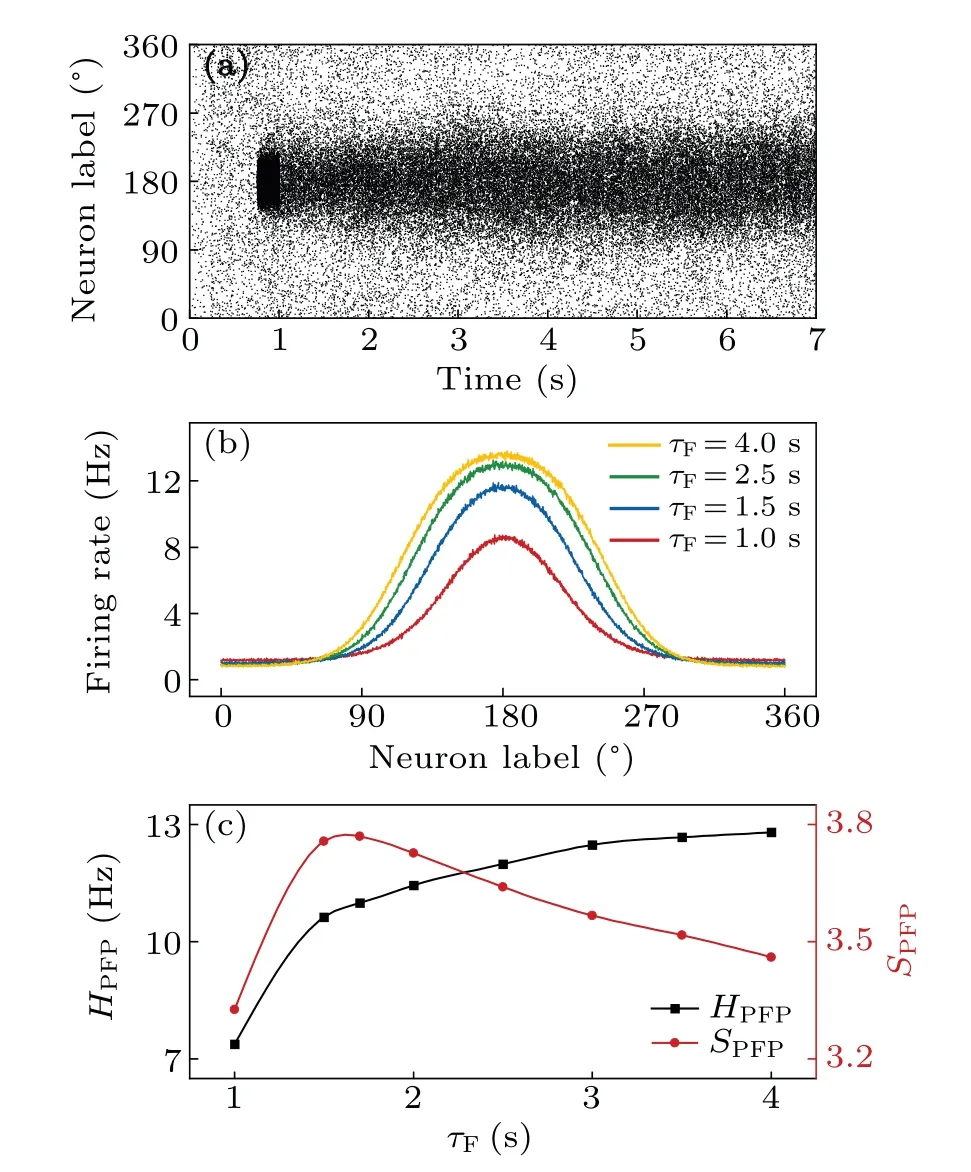
Fig.3.Spatiotemporal firing patterns of pyramidal cells with τD =200 ms.(a) Raster plot for principal cells with τF =1.5 s when a cue is presented at 180◦from 750 ms to 1.0 s.There are 2048 pyramidal cells labeled by their preferred directions and arranged along the y-axis in order.Dots on each row mark spikes of that neuron.(b)Population firing profiles for different τF values.The firing rate of each pyramidal cell is an average over the whole delay period and over 100 trials.(c) Height (square) and sharpness (circle) of the population firing profile versus τF.

The results above indicate thatτFandτDexert opposing controls over STP.In the following,τDis typically set at 200 ms unless otherwise specified in Subsection 3.4, whileτFis varied to explore the impact of synaptic plasticity on the maintenance of visuospatial working memory.Before cue presentation, the network exhibits homogenous sparse firing at a few Hz [Fig.3(a)].Given the cue located atθc=180◦,the neurons with preferred directions aroundθcare activated to persistently discharge during the delay period, while others with preferred directions far away fromθcare greatly suppressed.Thus, a bump attractor is maintained to encode the cue location, which is attributed to the slow recurrent excitation driven by NADARs and strong global inhibition mediated by GABARs.[7]

We calculated the mean firing rate of each pyramidal cell over the whole delay period and obtained the population firing profile,which is bell shaped with the maximum aroundθcand varies remarkably withτF[Fig.3(b)].The peak height elevates and the peak width enlarges with increasingτFdue to enhanced synaptic transmission.Quantitatively, the PFP can be characterized by its heightHPFPand sharpnessSPFP; with increasingτF,HPFPincreases towards saturation, whileSPFPfirst increases and then decreases[Fig.3(c)].

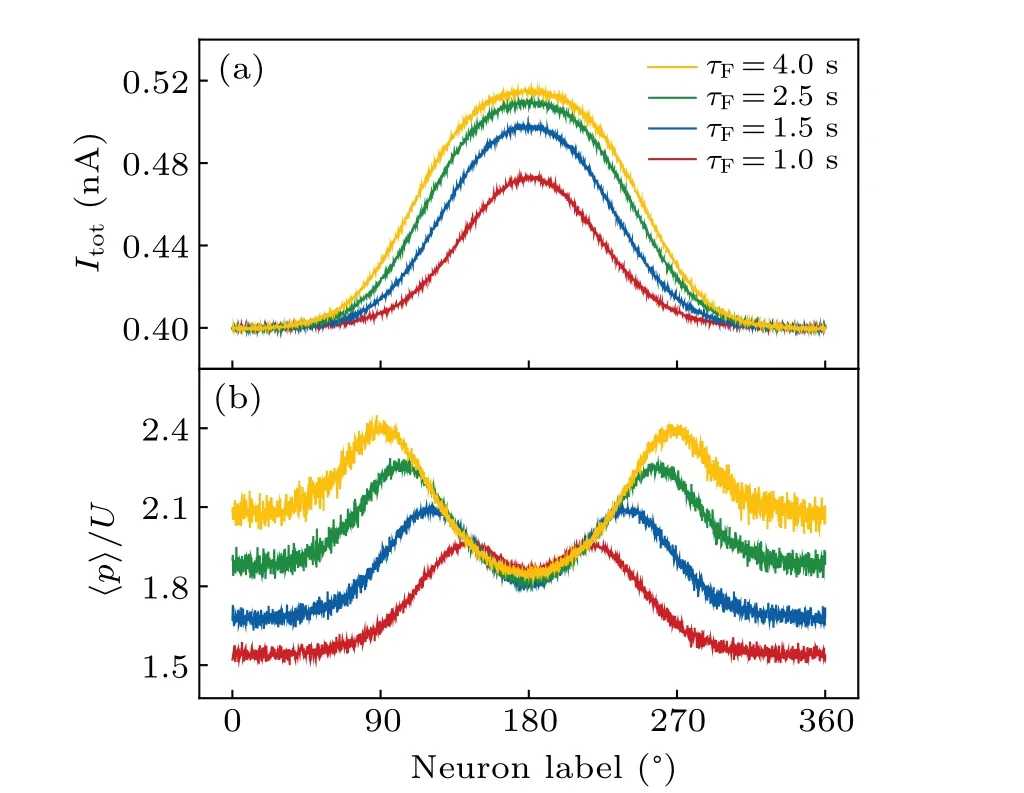
Fig.4.Synaptic mechanism for persistent activity during the delay period.(a) Total current and (b) synaptic plasticity (averaged over the delay period) for each pyramidal cell for different τF values with τD=200 ms.

The changing trend described above can be understood as follows.The short-term plasticity modulates the balance between excitation and inhibition in the network.As can be seen in Fig.4(a), the total current (Itot) for each neuron within the bump attractor increases with greaterτF.AtτF=500 ms,Itotis relatively uniform across the pyramidal cells(data not shown),and no bump attractor emerges.ForτF≥1.0 s,stronger shortterm facilitation leads to the activation of more neurons firing at higher rates.This enhanced local excitation activates more neurons near the edges of the attractor.Since synaptic facilitation becomes limited at high firing rates(Fig.2),the highest synaptic efficacy does not appear aroundθcbut rather on either side ofθc,especially at largerτFvalues[Fig.4(b)].Thus,the curve ofItotversus neuron index becomes wider and flatter aroundθcasτFincreases.This leads to a decrease inSPFPat largeτF.Overall,largerτFvalues give rise to stronger synaptic efficacy,resulting in higherHPFP,but cause the current profile to broaden,thereby constrainingSPFP.

3.3.Robust memory storage and sensitivity to cue presentation

The robustness of bump attractor dynamics is crucial for working memory,making it necessary to investigate its stability over time, specifically its resistance to random drifts and distractions.Due to the circular symmetry in synaptic connectivity strength and randomness of background inputs, the peak location of the bump attractor(θP)shifts randomly over time,resembling a diffusion process[Fig.5(a)].We conducted 100 simulations of the same mnemonic task and calculated the standard deviation ofθP,σP.AlthoughσPtends to increase across the delay period, its magnitude is sufficiently small(around 9◦at 6 s)[Fig.5(b)],which is attributed to STF.Indeed,σPat 6 s decreases with increasingτF[Fig.5(c)].Nevertheless,the decline becomes less pronounced forτF>2.5 s,suggesting a limited role for simply enhancing STF.Overall,STF plays a beneficial role in mitigating the random drift of the bump attractor.

Fig.5.Random drifts of the bump attractor during the delay period with τD =200 ms.(a) Time courses of the angle of the population activity vector on 100 simulations for τF=1.5 s.(b)Temporal evolution of the standard deviation of θP,σP.The data are from the same simulations as in(a).(c)σP at 6 s versus τF.

The resistance of the bump attractor against a distractor also reflects its dynamic stability.The distractor-related input has the same strength and duration as the cue-related input.Specifically, the cue is presented atθc=90◦, while the distractor is presented atθd(somewhere between 90◦and 270◦)from 3.75 s to 4 s.After the removal of the distractor, three scenarios may emerge: 1) the bump attractor centers aroundθd, leading to memory loss [Fig.6(a)]; 2) the bump attractor remains centered aroundθc,preserving the memory of the cue [Fig.6(b)]; 3) the center of the bump attractor lies betweenθdandθc,resulting in a bias in cue memory[Fig.6(c)].The occurrence of each scenario depends on various factors,such as background inputs,the angular difference between the cue and distractor (θcd=|θd-θc|),τFandτD.To quantify the deviation of memory storage,we calculated the difference inθPbefore and after the distractor presentation, denoted as∆θ=|θ1-θ2|.Considering the slow process of synaptic plasticity,θ1represents the peak location of the bump attractor right before the distractor onset, whileθ2is that at 3 s after the distractor offset.An average of ∆θover 100 trials is also taken and denoted as∆θ.

Forθcd=45◦or 90◦, although the cue- and distractorrelated inputs share the same strength and duration, it is generally more difficult to evoke and maintain a new bump attractor aroundθd, especially at largeτFvalues, due to the enhanced local excitation around the existing bump attractor and the dominance of global inhibition [Fig.7(a)].Indeed,only scenarios 2 and 3 appear forτF>1.0 s, and the likelihood of scenario 2 improves with increasingτF[Fig.7(c)].Forθcd=135◦or 180◦,the pyramidal cells aroundθdmay be easily activated to win the competition with the prior bump attractor atτF=1.0 s[Fig.7(b)].However,atτF=2.0 s,only scenarios 3 and 2 emerge forθcd=135◦and 180◦,respectively[Fig.7(c)].

Figure 7(d) shows the dependence of ∆θonθcdandτF.Atθcd=90◦,∆θfrist declines markedly and then gradually tends towards saturation with increasingτF(see the inset).The saturation occurs because the release probabilityucannot increase beyond 1,limiting the extent of STF.For fxiedτF,F∆θincreases with increasingθcdup to 135◦; atθcd=180◦,∆θdepends remarkably onτF.IncreasingτFfacilitates reducing the deviation, especially atθcd=180◦.Altogether, the network’s robustness against drift and distraction is enhanced with largerτF.

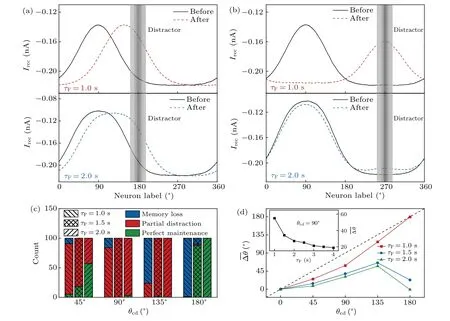
Fig.7.Resistance of memory storage against distraction with STF.(a) and (b) The average of recurrent currents over 100 trials for each pyramidal cell before(solid line)and after(dashed line)distraction for τF=1.0 s(upper)or 2.0 s(lower)and θcd=90◦(a)or 180◦(b).The gray rectangle marks the distractor position.(c)Distribution of three scenarios for different θcd and τF values.Here,memory loss and perfect maintenanceseparately correspond to ∆θ/θcd ≥0.8 and ∆θ/θcd ≤0.2.(d)∆θ versus θcd for different τF values.The inset shows∆θ versus τF withθcd=90◦.

In addition to the attractor stability, the network’s sensitivity to cue presence is also worth probing.As mentioned earlier,I0=500 pA is sufficient for a cue to evoke a bump attractor, where the mean and variance ofLPare denoted asmL,500andσL,500,respectively.Regardless of the cue intensity,only states withLP>Lth(=mL,500-3σL,500)are regarded as memory states.[18]The occurrence probability of the memory state quickly increases towards saturation with increasingI0[Fig.8(a)],and the minimum strength required for 95%occurrence is labeled asImin.AtτD=200 ms,Imindecreases with increasingτF[Fig.8(b)].This heightened sensitivity to cues still stems from the enhancement of synaptic efficacy.Note thatIminapproaches zero atτF=2.5 s,indicating that the network is hypersensitive.Without cue inputs, the STF is sufficiently strong with highτF, allowing certain pyramidal cells to predominate over others when activated by random background inputs.This, along with strong recurrent excitation and global inhibition from interneurons, can lead these cells to discharge persistently.In this case, the attractor center becomes entirely random.This result suggests a potential side effect of excessive STF.

3.4.Enhancing STD deteriorates the WM performance

We have probed the network behavior by varyingτFwhile keepingτDfixed at 200 ms.Here, we further examined how working memory is affected by varying the time constant of short-term depression.AsτDincreases, the profile of the bump attractor becomes lower, while suppressed pyramidal cells beyond the attractor instead elevate their firing activity[Fig.9(a)].Accordingly,HPFPdecreases with increasingτD,whileSPFPfirst increases and then decreases[Fig.9(b)].The minimal cue strength required for the memory state also increases with increasingτD[Fig.9(c)], indicating a reduced sensitivity to cue detection.The random drifts of the bump attractor become more prominent with increasingτD[Fig.9(d)].When the angular difference between the cue and distractor is 90◦,∆θalso increases with increasingτD[Fig.9(d)].In contrast toτF, increasingτDweakens the robustness of working memory and the network’s sensitivity to cue presentation.

Fig.9.Network behavior with τF=1.5 s.(a)Population firing profile for different τD values and(b)the corresponding HPFP and SPFP versus τD.The firing rate is averaged over the whole delay period and over 100 simulations.(c)Imin versus τD.(d)σP at 6 s(diamond)and ∆θ with θcd=90◦(triangle)versus τD.

Indeed,τDandτFexert opposing controls over transmission effciacy and ultimately on working memory performance.LowerτDensures a continuous supply of neurotransmitters over time,enhancing the synaptic effciacy,whereas higherτDresults in a neurotransmitter shortage, reducing the effciacy;higherτDhas a similar effect to lowerτFin terms of limiting the effciacy.Consequently,τDandτFhave opposite influences on the short-term plasticity.As a result,lowerτDstrengthens the robustness of working memory,similar to higherτF.

4.Discussion

In this study, we systematically examined the impact of short-term plasticity on working memory in the oculomotor delayed response task.Short-term plasticity comprises two components: short-term facilitation,which enhances the neurotransmitter release probability, and short-term depression,which restricts the depletion of neurotransmitters from recovery.These two components act in opposition at the single synapse level.Consistently, increasingτFor decreasingτDenhances the memory maintenance and sensitivity to cue detection.Compared to STD,excessively strong STF can render the network hypersensitive,while inadequate STF can result in the loss of the mnemonic state during the delay period.Suitable levels of STP are crucial for the network’s performance.

Numerous studies have demonstrated the role of STF in enhancing the stability of WM.For instance, STF markedly reduces the drifts caused by connectivity heterogeneity in a WM network.[19]STP improves network stability when the network suffers from synaptic connectivity defects.[20]Noise resistance can be improved when decoding a continuous attractor neural network with STF.[21]Differently, the current study offered a detailed analysis of network behavior over a wide range of STF levels and provides novel insight into the network’s stability against drifts and distractions and sensitivity to cue detection.

In a firing rate-based network model,STF and STD exert opposing effects on drifts caused by random firing or connectivity heterogeneity.[13]The current study confirms the contrasting functions of STF and STD and further investigated the network’s response to distractors and its sensitivity to cue presentation.Note that stronger STF alone leads to increased drifts when the effects ofτD-controlled STD are neglected.[9]Without STD, the synaptic efficacy improves monotonically towards saturation at individual synapses with increasingτF,and the profile of synaptic efficacy around the cue position is a plateau at higherτF, which amplifies local excitation and drives more neurons to fire at higher rates.Thus,the attractor is more prone to shift due to random background inputs.With both STF and STD in our study,however,the synaptic efficacy profile exhibits two peaks on either side of the cue direction,counteracting each other; this aids in preventing the attractor from drifting.

The sensitivity to cue presentation has a crucial role in WM.Mejiaset al.[22]reported that STF improves information retrieval in noisy neural networks.Consistent with theirs,our simulations showed a decrease in the minimal cue strength required for the memory state with increasingτF.However, at extremely highτF,the WM network still exhibits a mnemonic state even without a cue, resulting in a loss of cue detection.Therefore,achieving optimal WM performance necessitates a moderate level of STF,which enhances weak signal detection while preserving the ability to discriminate between cues and noise.

While the short-term facilitation mechanism in neural networks may share similarities with the excitation mediated by NMDA receptors, there are three key differences to highlight.First, the time scale of NMDARs ranges from tens to hundreds of milliseconds,[23]whereas STF can persist for minutes.[24]Second,NMDAR-mediated postsynaptic currents are voltage dependent and follow a second-order gating process,ultimately decaying to zero.[7]In contrast,STF involves the release of neurotransmitters from presynaptic vesicles,which is influenced by the release probability and available resources.The baseline release probability in the absence of presynaptic firing isU(nonzero).Third, NMDARs play an indispensable role in working memory, and impairments in NMDA function directly affect WM performance.[25]In contrast, while STF is known to reduce random drifts,[19]enrich neural firing patterns[26]and introduce interference from preceding trials,[10]it is not essential for the formation of attractors in WM networks.Instead, STF modulates WM by influencing its dynamics and performance.

The influence of short-term plasticity on working memory extends beyond its known complexity and functionality.Only the STP of NMDAR-driven currents is considered in our simulations, and the modulation of working memory could be further enriched by considering the STP of AMPAR- and GABAR-mediated currents.In addition,exploring other forms of STP holds promise for further insight.Developing a more comprehensive model would enable a deeper understanding and interpretation of complex cognitive tasks.

Acknowledgement

This study was supported by STI 2030-Major Projects 2021ZD0201300.