合理运用教学策略发展学生数学素养

⦿ 山东省东营市实验中学 刘桂林

在数学课堂教学中,教师需要转变观念,为学生营造一个和谐的学习氛围,通过创设有趣的教学情境、引入变式探究等多种教学策略来调动学生参与课堂的积极性,以此打造一个生动、有趣、高质的数学课堂.

1 巧借有趣的教学情境,让学生积极参与

创设情境是当前数学教学的重要手段之一.一个好的情境可以拉近学生与数学的距离,牢牢吸引他们的注意力,激发他们探索知识的积极性.那么,何为好的情境呢?笔者认为,好的情境应该是贴近生活的、符合学生认知的、能够诱发学生提出问题的,具有科学性、启发性和趣味性[1].教学中切勿为了情境而创设情境,那样不仅不能激发学生求知欲,而且可能会因为冗长繁琐而干扰学生注意力,影响学习效果.因此,教师在创设情境时应该从学生实际出发,反复打磨,进而确保情境适合本班学情,有效激发学生探究欲.

例如,在讲授圆有关的性质时,教师提出问题：“车轮为什么是圆的呢?”然后用动画模拟汽车装上三角形、正方形、椭圆形、圆形等不同形状轮子时汽车的行驶状态,并配有相应的声音.这样具有画面感的情境可让学生直观感受汽车只有配上圆形轮子才能平稳行驶,从而引出“同一个圆的半径都相等”的性质.

这样,将数学融于生活,让学生体会数学源于生活的道理,激发学生数学学习兴趣.同时,借助情境引导学生用数学思维思考问题,有利于提升学生学习品质,提升教学有效性.

2 巧借例习题潜在功能,让学生善于应用

例习题教学是数学教学的重要组成部分,其在巩固知识、强化技能等方面具有重要的价值.不过,在实际教学中发现,很多学生认为教材中的例习题较为简单,不具探究性,所以他们常常掌握解题思路后就草草了事.由于对例习题的不重视,学生难以发现例习题的潜在价值,影响了应用能力的提升.要知道,无论是平时考试,还是中考,很多题目中都有例习题的影子,因此在教学中应引导学生关注例习题的潜在功能,善于运用由陌生到熟悉的转化来提高数学应用能力.

图1

例1如图1,四边形ABCD是边长为3正方形,E为BC边上一点,且BC=2EC,P为BD上一动点,问点P在何处时,P到点E,C的距离之和最小?最小值是多少?

例1是一个动点问题,学生在解决一些动态的、探究性的开放问题时,容易产生畏难情绪.为了消除学生的畏难情绪,教师可以带领学生在教材中寻找原型,将陌生的、复杂的问题向熟悉的、简单的问题转化,以此来提升学生信心,激发数学学习兴趣.

例1给出后,教师没有给出具体的解题方法,而是让学生先思考如下问题：

例2如图2,为了给A,B两个小区提供牛奶,某奶制品公司准备在街道旁建一个奶站,问奶站建在何处可以使奶站到A,B两个小区的距离之和最小?

图2

图3

例2是学生非常熟悉的问题,在学习简单的轴对称图形时可以找到原型.该题给出后,学生很快找到了解题思路.如图3,作点A关于直线l的对称点D,连结BD交直线l于点C,点C的位置即为所求.从学生的反馈来看,该题几乎所有的学生都能顺利解答.学生顺利解答后,教师预留时间让学生寻找两道题目之间的联系,很快学生对例1就有了发现.

生1：作出点C或点D关于BD的对称点,问题就可以解决了.

图4

生2：根据正方形的性质可知C,A两点关于对角线BD对称,即A是C关于BD的对称点.如图4,连接AE交BD于点P,则P就是所求的点,PE+PC即为最短距离.

生3：求PE+PC其实质就是求AE.在Rt△ABE中,AB=3,又BC=2EC,故BE=1.5,根据勾股定理可求出AE的长.

这样在你一言我一语中,例1的解题思路已经呈现,学生的学习积极性被点燃.此时,很多学生感觉意犹未尽,于是教师顺势又出示了一道练习题：

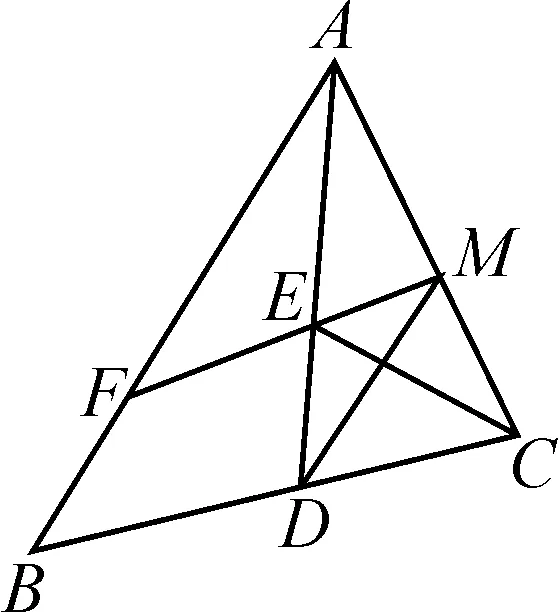
图5

例3如图5,AD是∠BAC的角平分线,且AF=AC,M是AC上任意一点,连接FM交AD于点E,连接MD,EC.求证：DC+DM>ME+EC.

有了前面问题的解题经验,很多学生将例3与前面的问题联系在一起,发现了解决此问题的方法,各个跃跃欲试地要举手发言了.

图6

生4：根据已知条件可知,点C关于AD的对称点是点F.如图6,连接FD,可知FD=DC,FE=CE,故问题可以转化为证明DF+DM>FM.因为DF,DM,FM分别为△MDF的三边,故DF+DM>FM成立,即DC+DM>ME+EC.

从学生准确、精彩的回答可以看出,通过由此及彼的探究,学生体会到若将知识联系起来,在运用时自然就如鱼得水了.

在教学中,教师要有意识地引导学生回头看,引导学生将相关的知识巧妙地联系起来,通过有效的对比分析找到解决一类问题的通法.学生在解决新问题时,可以借助联系将新问题转化为旧问题,从而通过经验的正向迁移顺利地找到解决新问题的方法,这样既能积累丰富的解题经验,又能提高迁移和联想能力,有助于提升解决问题的能力.

3 巧借变式教学,让学生勇于探究

变式教学旨在通过变化的问题探索不变的规律,探寻问题的本质,实现知识的融会贯通.数学问题是灵活多变的,有时变化一个条件就形成了一道新的问题.在教学中,对于一些典型性问题,教师可以巧妙地融入变式,从而让学生在变化的问题中去挖掘、去感悟、去探索,培养思维的灵活性、深刻性.

例4若a,b,c是实数,且a2+b2+c2-ab-bc-ac=0,求证：a=b=c.

证明：因为a2+b2+c2-ab-bc-ac=0,所以2a2+2b2+2c2-2ab-2bc-2ac=0.拆项配方,得(a-b)2+(b-c)2+(c-a)2=0.根据非负数的性质,得a-b=0,b-c=0,c-a=0,故a=b=c.

例4顺利证明后,教师在原有的基础上变一变,将其转化为一道新题.

变式1已知a,b,c是△ABC的三边,且方程(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)=0有两个相等的实数根,试判断△ABC的形状.

根据已知,将方程转化为关于x的一元二次方程后,由题意可知,Δ=[-2(a+b+c)]2-4×3×(ab+bc+ca)=0,即(a-b)2+(b-c)2+(c-a)2=0,分析至此,结合例4的经验易知△ABC为等边三角形.

变式2若a,b,c为△ABC的三边,且a3+b3+c3-3abc=0,求证：△ABC是正三角形.

变式3若a,b,c,d为四边形ABCD的四边,且4(a2+b2+c2+d2)=(a+b+c+d)2,试判断四边形ABCD的形状.

结合例4与变式1的解题经验,大多学生可以顺利地解决变式2与变式3.从以上解题过程可以看出,在解题时将式子转化为完全平方公式相加的形式,可巧用完全平方的非负性解决问题.

以上问题设计遵循由易到难、循序渐进的发展过程,既让学生在解决问题的过程中收获了学习信心,又让学生在变式探究中找到了解决此类问题的通法,有利于学生思维能力的发展和学习能力的提升.在解题教学中,教师应改变传统的就题论题式讲授,多从教学实际出发,巧妙设计一些变式问题,从而借助变式强化认知,达到通一题会一类的效果,有效提高学生解题能力.

4 巧借课外意外生成,让学生大胆猜想

课堂是动态变化的,课堂中可能会发生很多“意外”,而这些“意外”就是课堂宝贵的资源.“意外”中也许有学生思维的盲点和误区;也许有学生思维的闪光处;也许有教学漏缺;等等.在教学中,其实“意外”无处不在,只是大多教师为“赶进度”,常常忽视了这些“意外”,这样可能会影响学生提出问题、分析问题能力的提升,限制学生的长远发展.因此,在教学中,教师要及时捕捉这些意外,并进行深度挖掘,以此帮助学生消除盲点和误区,激发学习信心,有效提高学习品质和学习素养.

总之,数学教学过程应该是一个不断探索和完善的过程,在教学中要打破中规中矩的讲授,要千方百计地帮助学生获得成功的体验,让学生体会数学学习的乐趣,培养数学学习信心,让学生真正地融入课堂,提高教学有效性.