“预—解—探—结—悟”:数学习题教学新探索
——从一道习题的教学实践谈课堂提质增效的策略
邹守文
(南陵县城东实验学校,安徽 南陵 241300)
2021年7月印发的《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》强调,要优化教学方式,强化教学管理,提升学生在校的学习效率.因此,必须重视课堂教学,加强课堂教学管理,提高课堂教学效益.在“初中生数学核心素养差异性培养的研究”省级课题的研究中,笔者提出了“五步教学法”[1],有效提升学生的数学核心素养,能呼应“双减”背景下的教学新常态,实现提质增效.
课堂作为教学的主阵地,习题教学作为课堂教学的重要环节,在教学中除了要发挥习题的复习巩固、提炼变式、广泛应用等功能外,还承载了提升学生数学核心素养的功能.故应加强习题教学的研究,提高习题的教学价值.在平时的教学中要选择恰当的素材,对相关知识适度整合,在发展基础知识的同时兼顾发展能力,在注重数学活动的同时兼顾数学素养的提升.
在中考第一轮复习时,笔者选择了人教版《义务教育教科书·数学》(以下统称“初中《数学》”)(八年级下册)第69页第14题,通过课堂“五步教学法”的实施,让学生经历“预—解—探—结—悟”的全过程,在知识的发现、求解、变式、总结、感悟等一系列教学活动中,提高发现、提出、分析、思考和解决问题的能力,为课堂教学的提质增效提供有效保证.
例1如图1,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线于点F,求证:AE=EF.

图1
分析作为一道复习题,此题旨在巩固正方形的性质和全等三角形判定的相关知识,要求利用全等三角形的性质去证明两条线段相等.此题隐含了许多几何性质,能够链接相关知识,如全等三角形的判定和性质、相似三角形的判定和性质、勾股定理、锐角三角函数、线段的和差关系、线段的最值和四点共圆等.笔者选择此题旨在发展学生的推理能力、运算能力、几何直观等核心素养,同时引导复习课回归教材,整合、改编教材内容,拓展教材的应用价值,发掘知识的生长点.
1 预——通过预设的问题,激发学生自主学习的动机
《礼记·中庸》指出,凡事预则立,不预则废.教师在全面了解学生的认知规律、知识掌握情况,深入分析教材和学生“最近发展区”的前提下,从《义务教育数学课程标准(2022年版)》出发对教学内容进行分层预设,让学生对所学内容进行预习,并尝试解决预设的问题.“预”要求教师课前收集有效的信息,并对信息进行分析和处理.
在教学前一天,教师布置作业,要求学生完成初中《数学》(八年级下册)第69页第14题,并要求学生结合已学知识,采用不同的方法去证明问题,同时希望学生能够根据所学知识,结合已知图形,提出不同的问题.第二天,教师对学生的预习情况进行梳理,发现了学生的4种思路.
思路1如图2,取边AB的中点G,联结EG,可得△AGE≌△ECF,从而AE=EF.

图2
思路2如图3,过点E作EH⊥BC,且EH=CE,过点H作HM⊥AB于点M,则四边形BEHM是正方形,可得△AHE≌△FCE,从而AE=EF.
思路3如图4,过点F作FN⊥BC于点N,由思路2知∠1=∠2,可得△ABE≌△ENF,从而AE=EF.

图4
思路4如图5,联结AC,AF,可得∠ACF=∠AEF=90°,从而点A,E,C,F共圆,于是∠AFE和∠ACE为同弧所对的圆周角,∠AFE=∠ACE=45°,因此,△AEF为等腰直角三角形,故AE=EF.
由于学生对知识理解的程度不同,获得的体验也不同,从而思路也不同,但这些思路的获得恰好体现了学生对知识掌握的差别.
2 解——在问题的求解过程中,培养学生主动学习的能力
教师将“预”中的问题归类整理后,在课堂教学中,对预习过程出现的问题分层精讲.在“解”的环节中坚持以学生为主体,教师起引导、连接和点评的作用.在分析和点评的过程中关注学生的行为,重视师生互动、生生互动,立足学生回答问题中的“学情”,通过“解”和点评的过程引领学生差异性素养的发展.
在教学中,教师把例1的中点改为任意点,继续探究题目中AE与EF的数量关系.通过几何画板软件的演示,发现仍有AE=EF,如何去证明呢?
变式1四边形ABCD是正方形,E是边BC上的任意一点,∠AEF=90°,且EF交正方形外角的平分线于点F,求证:AE=EF.
教师引导学生探究.5分钟后,学生分组汇报证明思路,得到和例1类似的5种思路.
思路1如图6,在边AB上截取BG=BE,得到△AGE≌△ECF,从而AE=EF.
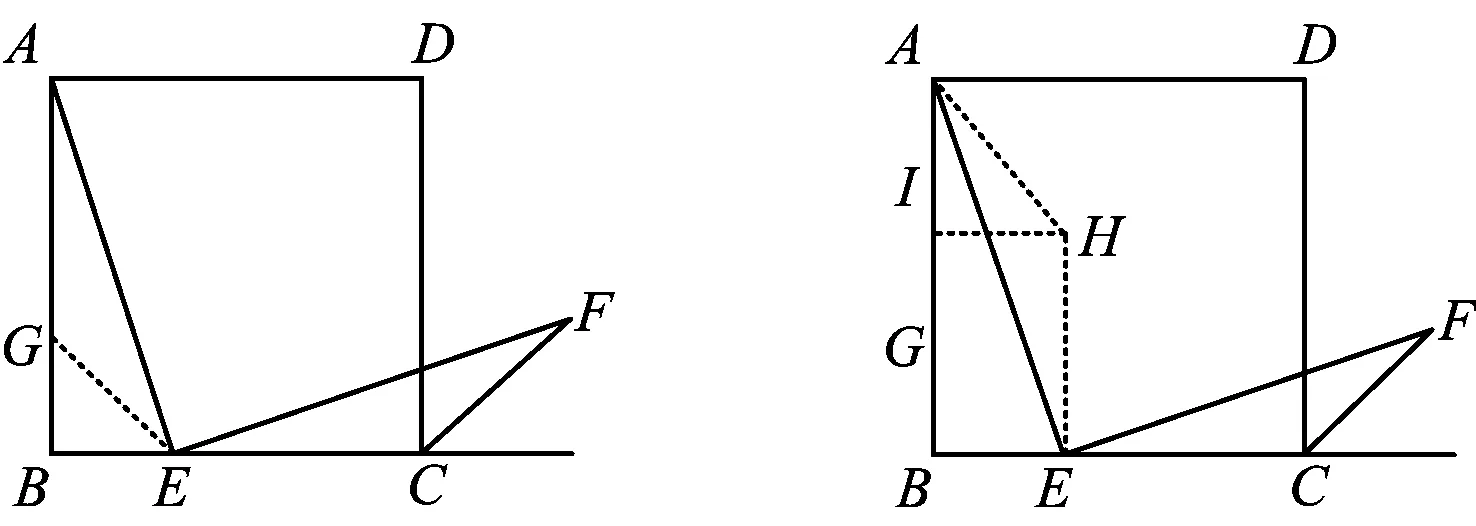
图6
思路2如图7,过点E作EH⊥BC,且EH=EC,得到△AHE≌△FCE,从而AE=EF.


图8
思路4如图9,延长FE,AB相交于点K,过点F作FM⊥BC于点M,利用射影定理可以转化为思路3.
思路5如图10,联结AC,AF,有∠ACF=∠AEF=90°,从而点A,E,C,F共圆,于是∠AFE和∠ACE为同弧所对的圆周角,∠AFE=∠ACE=45°,因此,△AEF为等腰直角三角形,故AE=EF.
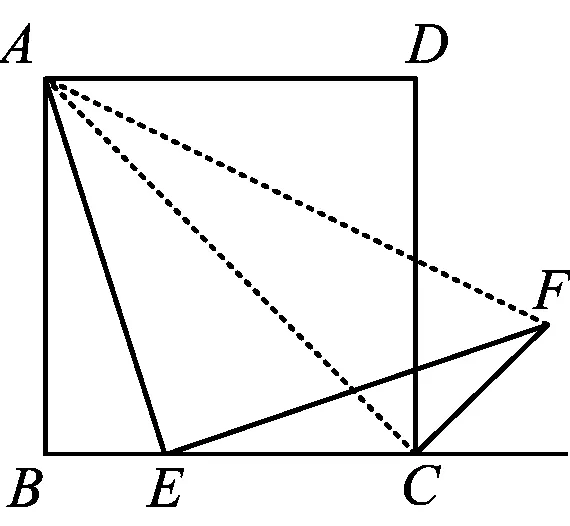
图10
3 探——在知识的探究过程中,激发学生思维的活力
在师生共同努力下,将精讲的内容进行“变式”“拓展”,通过变式、拓展、升华等手段,强化对知识的理解与掌握,固化知识的变式功能.变式拓展的方法可以是一般化与特殊化的转化、数字与字母的替换、已知与结论的互换、条件的增减、图形的几何变换等.在“变—探”的过程中,使不同学生的数学核心素养得到不同的发展.改变问题的题设和结论,进行深度探究,弄清问题的相互关系和本质特征.
3.1 变线段垂直为线段相等,探究垂直关系
把例1中的条件“∠AEF=90°”改为“AE=EF”,把求证“AE=EF”,改为求证“∠AEF=90°”,同时就一般情形进行探究,研究证明思路.
变式2如图11,点E为正方形ABCD的边BC上一点,联结AE,过点E作EF使EF=AE交正方形的外角平分线于点F,求证:∠AEF=90°.

图11
分析此时没有垂直的条件,故很难构造相似三角形或锐角三角函数,直接的思路是利用勾股定理去建立方程,通过解方程透析其中的数量关系.
证明过点F作FM⊥BC于点M,设AB=a,BE=x,FM=CM=y,则
AE2=a2+x2,EF2=EM2+FM2,
从而
a2+x2=(a-x+y)2+y2,
解得y=x.进一步得到
△ABE≌△EMF,
从而
∠AEF=90°,
即
AE⊥EF.
3.2 把垂直和相等两个条件合并,证明点F在外角平分线上
变式3点E为正方形ABCD的边BC上任意一点,把AE绕点E顺时针旋转90°到EF,求证:点F在正方形外角平分线上.
思路1如图12,在AB上截取BG=BE.
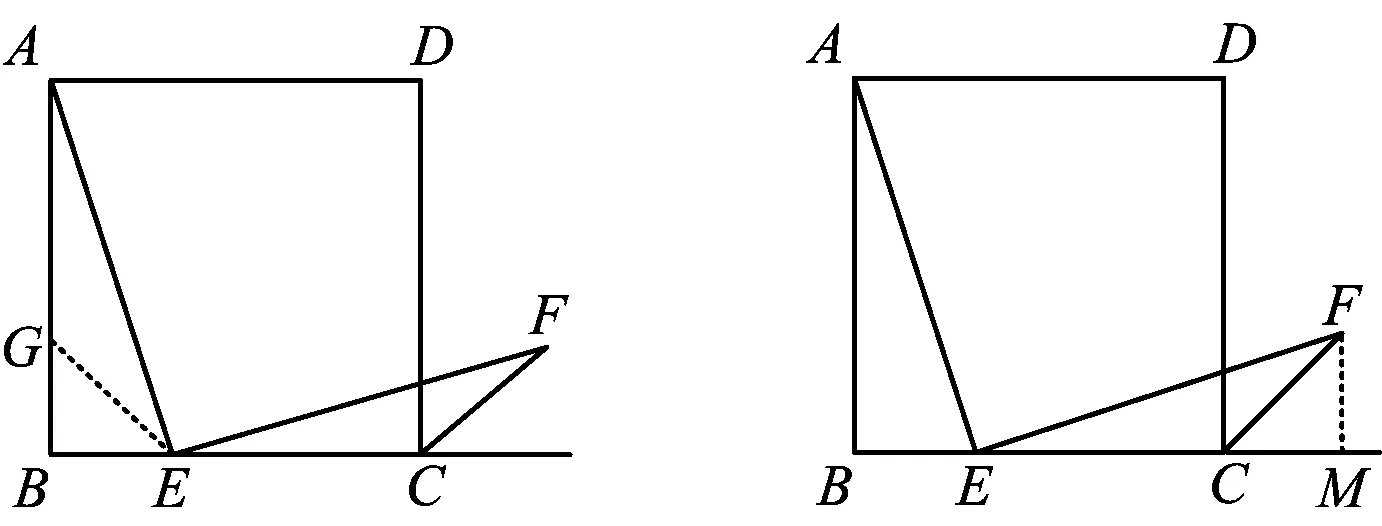
图12
思路2如图13,过点F作FM⊥BC于点M.
3.3 联结AF交CD于点G,探究点G在CD上的位置关系

变式4如图14,点E为正方形ABCD的边BC上的一点,联结AE,过点E作∠AEF=90°,交正方形的外角平分线于点F,联结AF交CD于点G,设BE=kBC.
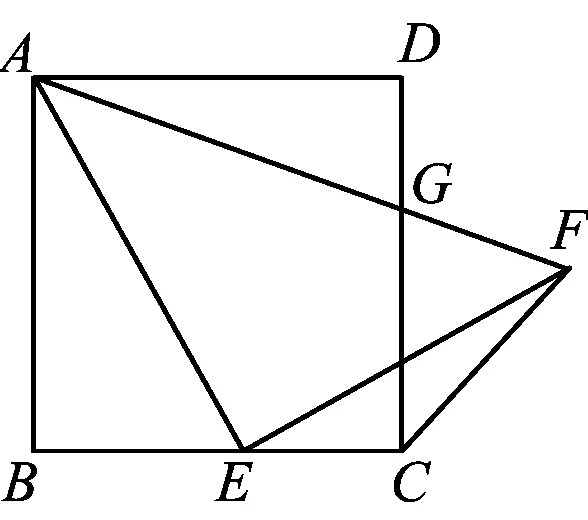
图14
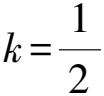


3.4 联结DE,设DE中点为Q,求PQ的最小值
变式5如图15,四边形ABCD是正方形,AB=4,点E是边BC上一点,将线段AE绕点E顺时针旋转90°,得到线段EP,点Q是DE的中点,联结PQ,求PQ的最小值.

图15
4 结——通过总结,强化学生归纳反思的意识
教师采取学生自评、学生互评、教师点评等方式,引导学生谈谈收获,不是简单地罗列知识点,而是继续发挥学生的学习主动性.在自评与互评的过程中,让学生感受该课时的学习现状,找出这节课学习的得与失,还有哪些困惑和不足.这种方式不仅提醒学生在课堂学习中要注重学习过程,更重要的是让学生“思考”学习过程.
通过对这节课和已学相关内容的小结,获得以下结论:
四边形ABCD是正方形,点E是边BC上任意一点.
1)若∠AEF=90°,且EF交正方形外角的平分线于点F,则AE=EF.
2)联结AE,作EF,使EF=AE交正方形外角平分线于点F,则∠AEF=90°.
3)把AE绕点A顺时针旋转90°到EF,则点F在正方形的外角平分线上.

结合前面学习的知识,思考还能得出哪些结论?
如图16,点E为正方形ABCD的边BC上任意一点,联结AE,过点E作EF⊥AE交正方形外角平分线于点F,
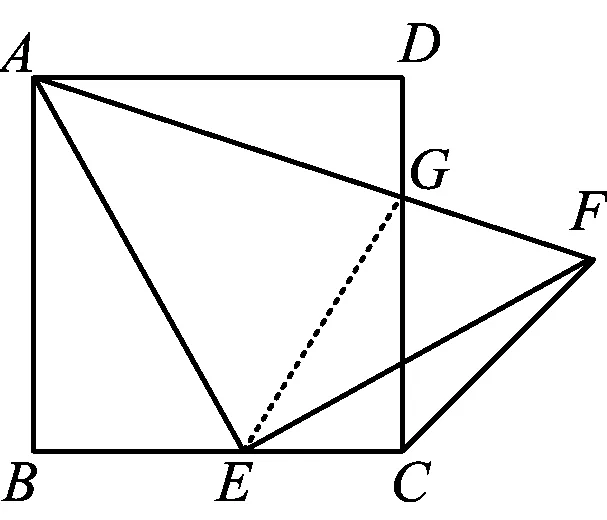
图16
5)∠FAE=45°,△AEF是等腰直角三角形.
6)设AF交CD于点G,联结EG,则DG+BE=EG.
7)设AF交CD于点G,联结EG,则EF平分∠CEG.
8)如图17,联结BD分别交AE,AF于点M,N,则:

图17
①BM2+DN2=MN2,线段BM,MN,DN可以作为直角三角形的3条边;
②△ABN∽△MDA,BN·DM=AB2.
9)在7)的条件下,点A,E,C,F共圆.
5 悟——通过感悟深化对知识的理解,提升学习能力
通过对学习的再反思,形成对知识更深层的理解,提升对知识理解的再升华.在此基础上,对学生这节课的课堂内容做具体要求,即布置课后任务,既能检测这节课的学习效果,又为下节课的教学做一定的铺垫.
在这节课的最后,教师要求学生将所学习的知识在大脑中“过一遍”,看一看有哪些知识已经掌握、哪些知识是自己没有想到的、这节课有哪些体会?这节课是对教材的“回炉”,其中涉及的是一个基本的图形.学生在前面的学习中已经多次接触这个图形.接下来教师要求学生结合此次教学,看看这个图形中还蕴含了哪些性质,把自己的感悟写下来,并由教师点评.
通过学生的反思和感悟,又有以下收获:


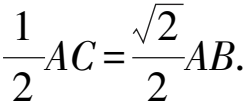
4)如图18,在变式1的条件下,联结BD,交AE,AF于点G,H,则:
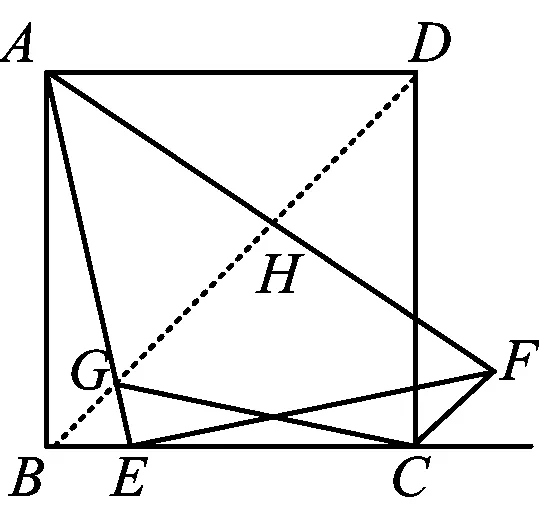
图18



6)点E在边BC的延长线上时,其他条件不变,AE=EF仍然成立.
习题是教材编写者精心设计的.教师对习题的教学不能一蹴而就,因此,要尊重学生的认知规律和知识结构,科学设计、有效推进、螺旋式上升,让学生亲历习题教学的整个过程.要以习题为“脚手架”,引领学生自主探索,培养学习兴趣,激发学习热情,提升核心素养和学习潜能.
例1的图形是一个基本图形.在“预”的阶段,教师把问题抛给学生,对例1进行“回炉”.学生已经学习了一些新的知识,包括相似三角形的判定和性质、锐角三角函数的求法、四点共圆等.因此,以例1为知识的生长点,希望能碰撞出思维的火花.在对“预”的梳理过程中发现了学生思维的多样性,也为后面环节的展开奠定了基础.
由于中点的特殊性,自然想到“当点E为线段BC上的任意一点,AE=EF是否成立”.通过几何画板软件的演示,发现结论仍然成立.接下来就是寻求相等关系的证明,让学生结合自己的独立思考和小组合作探究,碰撞出5种思路,很好地体现了“解”的环节的作用——培养学生主动学习的能力.
命题和逆命题是几何研究的常用方法,改变变式1的题设和结论可以得到两个不同的命题,它们是否成立呢?借助几何画板软件的演示功能,发现在相等条件下,直线的垂直关系仍然成立;再将垂直和相等作为条件,变换问题的表述形式,以旋转的方式将两个条件整合起来,探究点F是否在正方形的外角平分线上,逐步深入,把“预”和“解”两个环节无缝对接,过渡到“探”的环节,这样培养了学生自主学习的能力.但课堂并没有就此结束,而是乘胜追击,通过联结AF交CD于点G,探究点G在CD上的位置关系.这样把课堂引向深度学习,接着“联结DE,设DE中点为点Q,求PQ的最小值”.这样对变式1进行变式,提升例1的价值,从而使学生的知识内化为能力,能力固化为素养.
“结”的环节是对知识的小结,本节课的小结有正在获取的知识,也有对前面所学知识的回顾和总结,实际上是对图形性质的系统总结,是一个提高的过程,是数学学习过程中非常重要的环节.通过小结归纳出图形的9条性质,基本囊括了正方形中45°角的性质,每一个性质都可以独立作为一个命题,训练学生“有逻辑地思考问题”[3],同时加强相关性质的整合,提高解决问题的能力.
“悟”的环节是课堂教学过程的延续,作为课堂教学的有效补充.通过自我反思和感悟,学生能够实现知识的升华:在特例的启发下建立一般性规律,探究问题存在的条件,发掘图形运动的路径,还可以获取更多的结论,从而使课堂行为得到升华.
“五步教学法”中的“五步”不是相互割裂的,而是一个有机的整体.“预”作为“五步教学法”的起始环节,起着承上启下的作用,它既是“悟”的延续,又连接着“解”和“探”,是课堂顺利进行的润滑剂;“解”是学生学习行为的直接反馈,通过“解”了解学生的学习情况,是有效调节课堂、科学实施“探”的保证,是高效课堂的助推剂;“探”是教学环节的重点,是一节课的灵魂,“探”的质量决定了一节课的效果,是高效课堂的兴奋剂;“结”是学生对课堂学习的主观反映,是对自己学习的一个客观评价,实现了“教—学—评”的一体化;“悟”是课堂教学活动的延续,是学生将所学内容经过自己的消化、吸收和反刍,转化为自己的思路和方法的过程,是课堂教学的催化剂.
只有坚持五步并举,才能落实“五步教学法”,提升学生的数学核心素养,实现课堂教学的提质增效.

