精研真题一题多解 洞察结构二度创造
沈建新
(德清县第三中学,浙江 德清 313201)
常态化的习题教学基于传统解题教学的“就题论题”,往往忽视对试题潜在价值的发掘,没有对试题进行更深层次地探究,严重束缚了学生的思维发展.那么在教学实践中如何有效地开展习题教学,才能切实发展学生的数学关键能力,提升数学核心素养呢?本文以一道中考真题为切入点进行探讨.
1 真题呈现与分析
1.1 真题呈现
例1如图1,四边形ABCD内接于⊙O,对角线AC,BD相交于点E,点F在边AD上,联结EF.

图1
1),2)略.
3)①略;
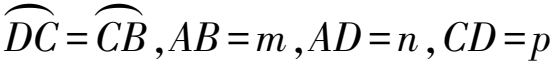
(2022年湖南省长沙市中考数学卷第24题)
本文只探究最后一道小题.从试题的呈现形式来看,题干精练,图形简洁,似乎给出的数量关系与所求线段没有明显的关联.由于已知信息之间的联系是孤立的,且题中线段长度用字母形式呈现,学生不是很适应,以致思路受阻;在已知条件与所求线段之间出现思维断层,因而成为解题障碍.因此,解答此题需要从现有的已知条件中挖掘出隐含信息,通过有效转化进行深入分析,具有较高的思维含量,题目的区分度也能得以很好地体现.
1.2 真题分析
一个复杂的问题,若没有直接的解法,则可尝试在挖掘出更多的条件信息中,对隐含信息进行加工处理,在此基础上再来探究这些信息与所求问题之间的关系,有利于发现解法[1].
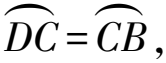
第二,从隐含信息思考,悟几何直观.根据“在同圆或等圆中,同弧或等弧所对的圆周角相等”,结合题中信息,可得
∠DAC=∠BAC=∠DBC=∠BDC,
∠DCA=∠DBA, ∠ADB=∠ACB,
由此可证
△DEC∽△AEB∽△ADC,
△DEA∽△CEB∽△CBA.
根据“相似三角形的对应边成比例”的基本性质,进而可以得到线段之间的一些关系,这样可以挖掘出更多的隐含信息,结合这些信息,为后续的解题做好思维准备.
在分析过程中,可以从“关键词句”和“隐含信息”这两个不同的思维起点引导学生,激发学生的有效思考.培养学生准确捕捉信息的能力,注重把握几何图形中隐含的特殊性质,为解题提供良好的切入点,引导学生“有逻辑地思考”,从而让学生拥有数学的思维.
2 真题的多维度探究
通过一个典型问题,启发学生从不同角度,运用不同思路、方法去分析和解答,这样的借题发挥训练,可以让学生的思维更宽广,逐步形成题感,提升解题能力.
思路1依托定理,类比迁移可得法.

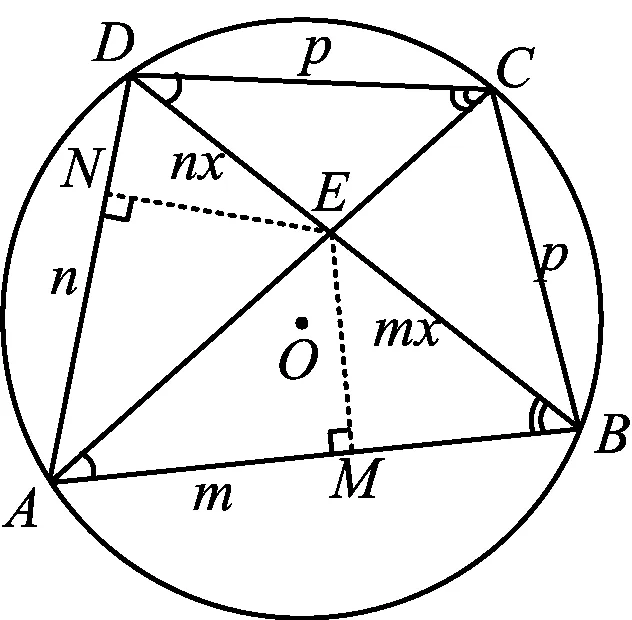
图2
EM=EN,
易得
设BE=mx,DE=nx,结合已知线段AB,CD和所求线段AE,CE,联想到可证明△CDE∽△BAE,得
从而
于是
AE·CE=mnx2.
由问题“试用含m,n,p的式子表示AE·CE”,执果索因,思考“x2”与“m,n,p”之间的关系.由△CDE∽△CAD,得
即
从而
整理得
故
思路2洞察结构,构造模型得思路.
解法2如图3,过点C作CM⊥AB于点M,CN⊥AD交AD的延长线于点N,易证
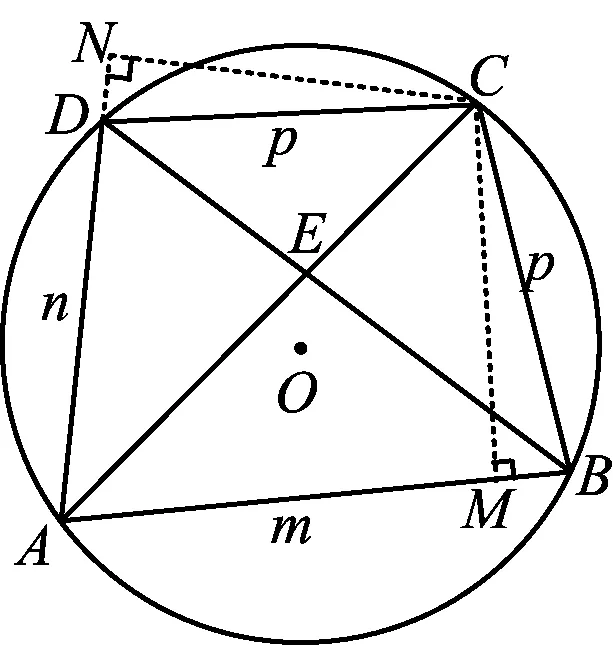
图3
△CND≌△CMB,
得
ND=MB.
因为△CAN≌△CAM,所以
AN=AM.
结合已知条件可得
设AE=a,CE=b,由CM2=AC2-AM2=CB2-MB2,得
整理,得
(a+b)2=p2+mn.
(1)
又由△CDE∽△CAD,得
从而
p2=ab+b2.
(2)
由式(1)和式(2)可得
a2-b2=mn-p2.

从而
得
即
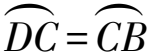
思路3由因导果,联想设参妙转化.
解法3如图4,易证△BEC∽△AED,得

图4
设BE=px,AE=nx.因为△CDE∽△BAE,得
则
所以
由△CDE∽△CAD,得
即
整理得
从而
思路4几何解法,合情推理自然成.
解法4如图4,易证△ABE∽△ACD,得
即
AE·AC=mn.
因为△CDE∽△CAD,得
所以
CE·AC=p2.
进一步可得CE·AC+AE·AC=p2+mn,
即
AC2=p2+mn,
且
AE·CE·AC2=mnp2,
从而
评注思路3和思路4都是从“隐含信息”思考,结合题中条件,由因导果,利用各种不同的三角形相似得到线段之间的一些关系,再通过设参法,从“独立”到“联系”,化“未知”为“已知”,把线段的长度置于“相似三角形”中进行合情推理,进而解决问题.
综上所述,通过一题多解,可以让学生体验解题方法的多样性.从题中“关键词句”和“隐含信息”两方面思考,既有通性通法,又有特殊技巧.教师应坚持恰当而适量地采用一题多解的方法进行思路分析,探讨解题规律和对习题进行多角度“追踪”,让学生“以少胜多”地巩固基础知识,切实提高分析问题的能力,掌握基本的解题方法与技巧[2].
3 基于真题的二度创造
3.1 基于“条件”改编的再创造,生长新问题
解题教学不仅需要变化,而且要善变,要会通过对试题“条件”进行改编,让学生对这些大变化和小变化产生兴趣,以启发学生的思维.
3.1.1 变更条件,挖掘新结论
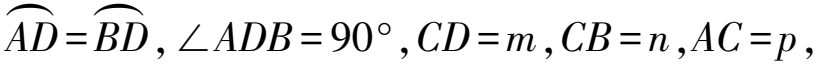
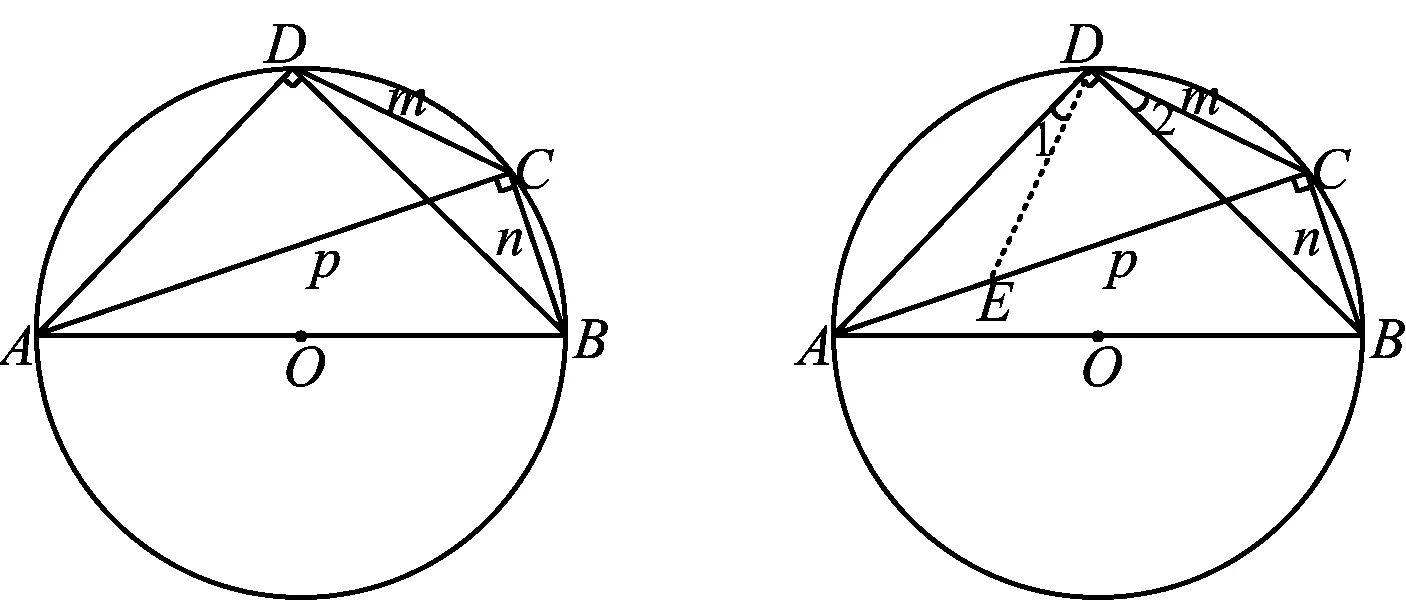
图5
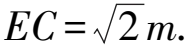
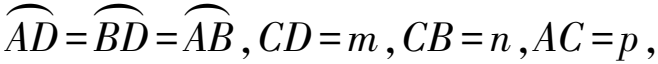

图7
证明如图8,在线段AC上截取AE=CB=n,联结DE.易证△DAE≌△DBC,得∠ADE=∠BDC,且DE=DC=m,从而∠EDC=60°,△DEC为等边三角形,则EC=m.因为EC+AE=AC,所以m+n=p.
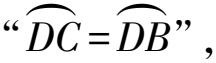
3.1.2 强化条件,探究新关系
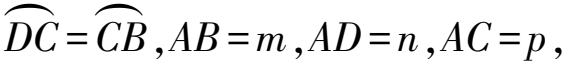
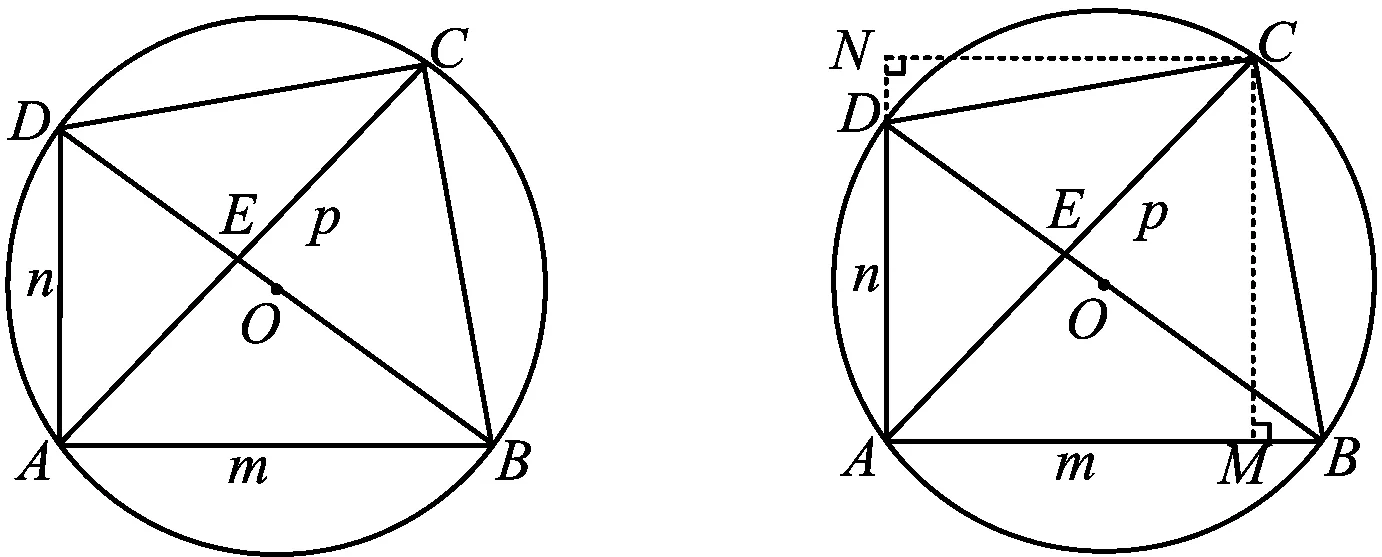
图9
证明如图10,过点C作CM⊥AB于点M,CN⊥AD交AD的延长线于点N,易证△CND≌△CMB,从而CN=CM.易得四边形NAMC为正方形,结合已知条件可得

评注上述生长问题将原题中的普通△ABD强化为“直角三角形”,借助“角平分线,轴对称”结构,作“双垂直”辅助线解决问题,进而探索线段之间的关系.
3.1.3 弱化条件,关联新定理
生长问题4如图11,若AB=m,AD=n,CD=p,BC=q,试用含m,n,p,q的式子表示AC·BD.
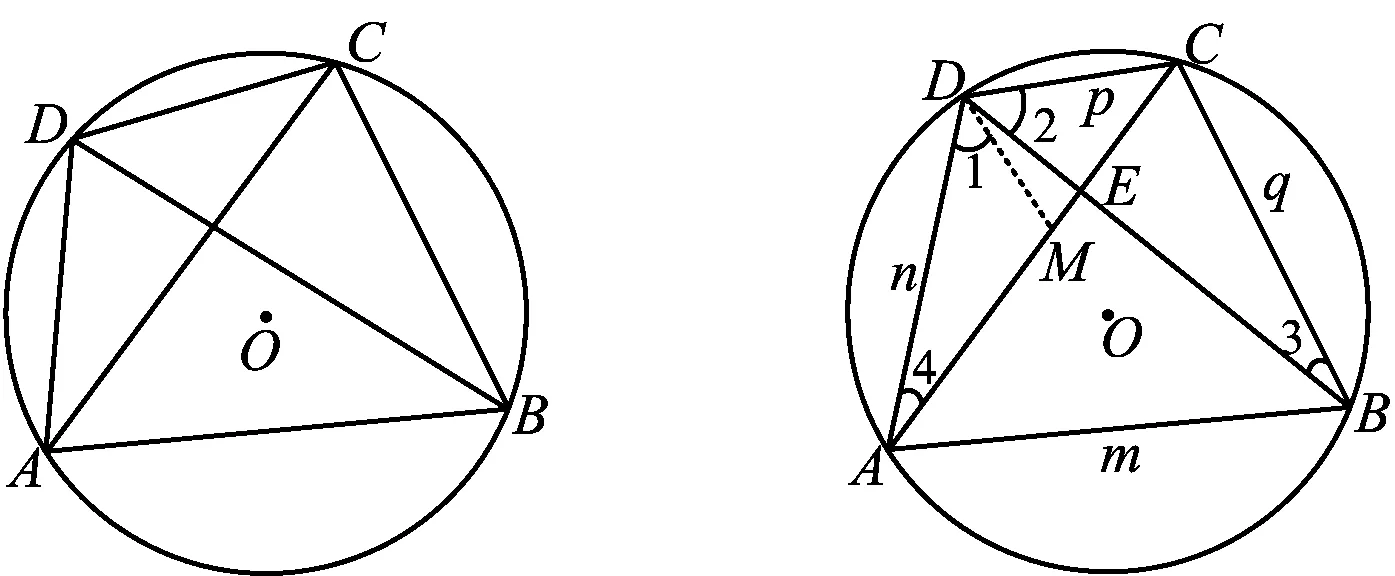
图11
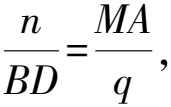
BD·MA=nq.
(3)
易得
∠MDC=∠ADB,
可证
△MDC∽△ADB,
得
即
BD·MC=mp,
(4)
式(3)+式(4),得
BD·(MA+MC)=mp+nq,
从而
AC·BD=mp+nq.
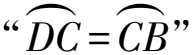
综上所述,基于试题“条件”的改编,可通过变更条件、强化条件、弱化条件,甚至改变条件的背景、隐藏条件或显示条件等手段尝试对试题进行再创造,以达到一题多变、一题多练的效果.
3.2 基于“结论”拓展的再创造,生长新价值
善于发现并挖掘图形的特征,学会用数学的思维思考,把“结论”再向前推进一步,经历数学“再发现”的过程.因此,借题发挥,通过“结论”来拓展延伸是关键一步.
3.2.1 深挖结论,化隐为显
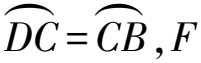
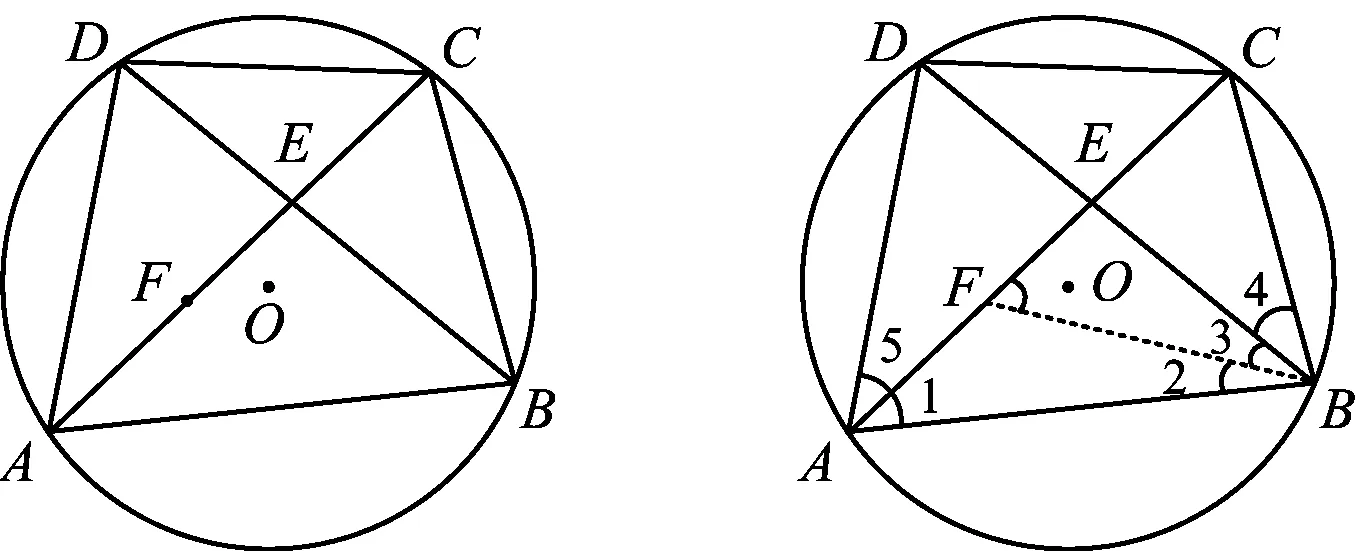
图13
证明如图14,联结FB,易得
∠2=∠3, ∠1=∠5=∠4.
因为∠CFB=∠1+∠2,∠CBF=∠3+∠4,所以
∠CFB=∠CBF,
得
CF=CB.
易证
△CEB∽△CBA,
得
即
CB2=CE·CA,
则
CF2=CE·CA.
评注由上述证明可知CD=CF=CB,故点D,F,B在以点C为圆心、CB为半径的圆上.
3.2.2 追本溯源,深思模型

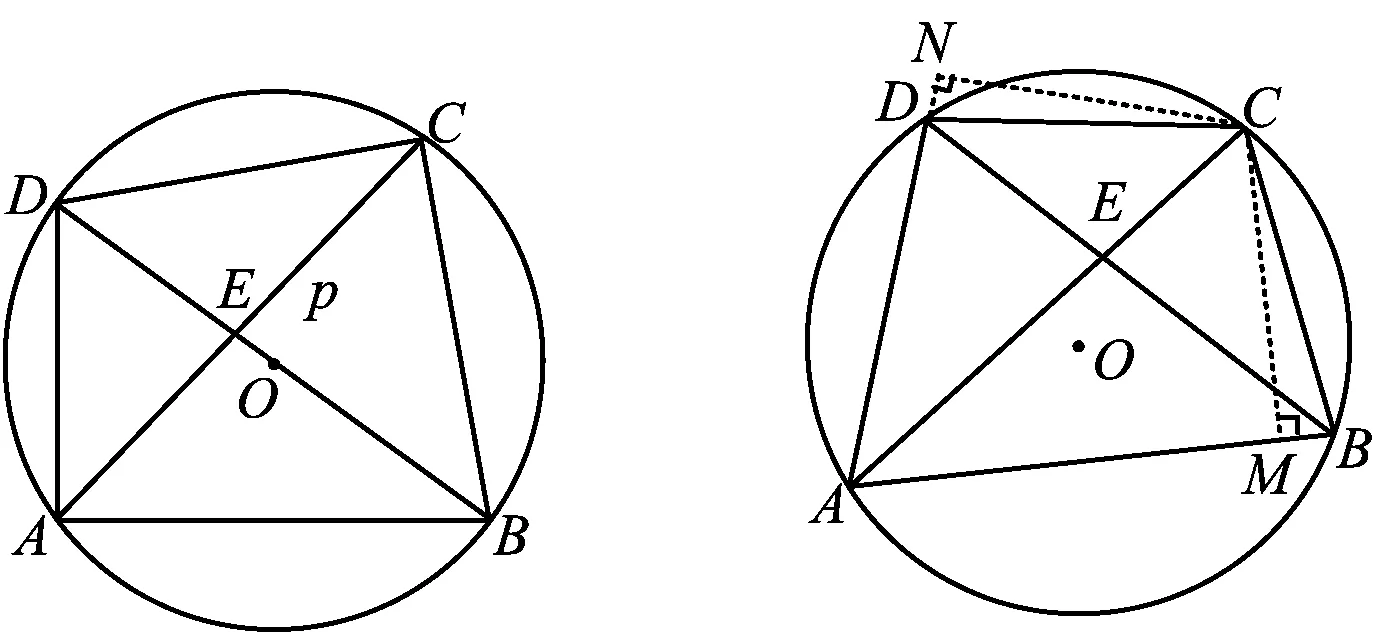
图15
证明如图16,过点C作CM⊥AB于点M,作CN⊥AD交AD的延长线于点N.易证
△CND≌△CMB,
从而
ND=MB,
于是AB+AD=AM+MB+AN-ND=AM+AN.
因为△ACN≌△ACM,得
AN=AM,
所以
m+n=2AM.
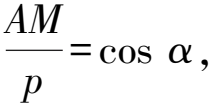
评注由题意可知,该基本图形包含角平分线、对角互补、邻边相等这3个结构条件,可知二推一.利用“角平分线”,可作“双垂直”辅助线;利用“对角互补”,可构造其中一个内角的邻补角,得等角;利用“邻边相等”,可借助“共端点,等线段”结构,通过旋转构造全等三角形.解决此类基本图形的相关问题,可引导学生深思模型,形成一定的处理策略.
3.2.3 洞察结构,溯源定理
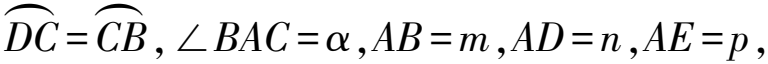

图17
证明如图18,过点E作EM⊥AB于点M,EN⊥AD于点N,过点D作DH⊥AB于点H.易得
S△ABD=S△ABE+S△ADE,
从而
则
整理得
mnsin 2α=(m+n)psinα.
因为sin 2α=2sinαcosα,所以
mn·2cosα=(m+n)p,
得
评析由上述探索可联想到张角定理,即如图19,在△ABD中,点E是边BD上的点,联结AE,则
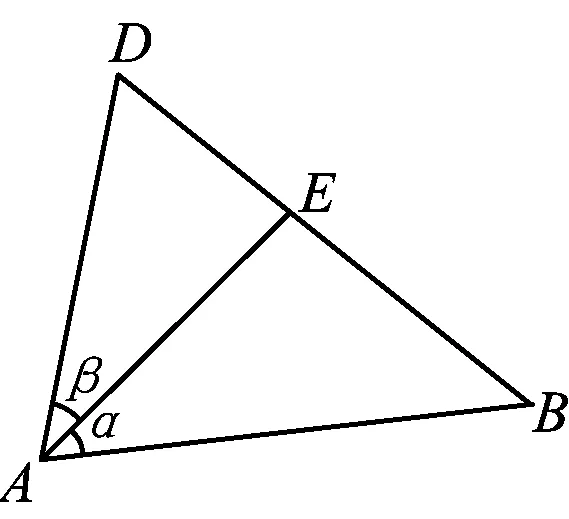
图19
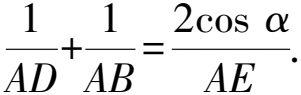
综上所述,基于试题“结论”拓展的再创造,深入挖掘隐含结论,可以开阔学生的眼界,发散学生的思维,增长学生的见识;还可以增强学生的整体意识,引导学生着眼于知识间的联系与规律,从系统的高度去把握知识、进行思考,做到八方联系、浑然一体.
4 基于思路设计的实践反思
学而不思则罔,思而不学则殆.从典型中考真题入手,深入探究,充分挖掘隐含的价值,然后进行必要的解后反思、归纳,对解题教学有极大的帮助.
4.1 精研真题,遴选经典于题海
在教学中,教师要跳出“题海战术”的怪圈,精心选取值得开发的中考真题或教材中的例题、习题,这就需要教师“先下题海”,从题海中筛选出经典题目.一道好的数学题应当是学生进行丰富数学探究活动的起点,它应该具有良好的结构和丰富的变化.具有良好结构的数学题一般有多种解题方法、多个核心知识交汇,蕴涵着重要的数学思想;题目的丰富变化可以将一道简单的“源问题”编织出一张精彩纷呈的知识网,在变化探究中,培养学生的数学思维,发展学生的问题意识[3].
4.2 二度创造,常现拓展于课堂
在教学中,我们可以将一个问题进行多角度再创造,由浅入深、由特殊到一般、由常规到灵活,以便让学生学会从问题之间的联系来理解问题的本质,在一定程度上减少思维的惰性与僵化,从而更深刻地理解与掌握数学知识.这就要求教师深度探究中考真题或教材中的例题、习题,善拓展,常更新,从一题出发延伸变式,得出各种新问题,目的不仅在于一个问题的解决,还在于通过解决一个问题融通一类问题,达成思路的拓展,并以此为载体培养学生思维的迁移能力.
4.3 归纳提炼,铭记策略于心中
在教学中,讲完一种方法,我们可以剖析方法步骤后面的思想,感悟方法之中的策略,将外在的学习内容转化为内在的知识力量.某些基本图形的固定处理策略往往是解题的关键.只有洞察图形结构,才能借助模型找到解决之道.引导学生从“问题”中来,到“模型”中去,生成相应的解题策略,更要多进行解题教学内容的整理、归纳与提炼,画思维导图,得解题套路.平时多注重积累与归纳,用时方能获得解题的灵感.
习题教学在当下的数学课堂教学中占有非常重要的比重.如何让习题课也能上得有趣味、上出新授课那样有“探索未知领域”的效果?这需要教师在课前做沉浸式探索,精心预设.教师通过一题多解、二度创造,使教学“少而精”,让学生有足够的时间进行练习,充分地在问题中探究、在探究中反思、在反思中发现、在发现中成长,从而全面发展数学关键能力,提升数学核心素养.

