以大观念为中心的数学单元教学策略
于 涛
(东莞中学,广东 东莞 523005)
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课标》)指出,重视以学科大概念为核心,使课程内容结构化,以主题为引领,使课程内容情境化[1].《课标》体现的课程理念需要教师实施单元整体教学,促进学科核心素养的落实.目前,数学单元教学在学理层面、概念层面、设计层面探讨较多,在应用层面还存在较多的问题.例如,单元教学内容联系不紧密,只是章节课时内容的简单堆砌,缺乏对知识结构的构建;又如,单元教学内容不聚焦,对学生迁移能力的培养体现不足;再如,教师对单元教学知识的本质理解不深刻,教学组织未遵循认知规律等.本文以大观念为中心,通过分析数学学科特点,结合笔者在教育教学中的思考,提出3种数学单元教学策略,意在丰富单元教学应用层面的研究.
1 以大观念为中心的数学单元教学思考
1.1 大观念的基本内涵
“大观念”源自对“big idea”的翻译,从国内学者对“big idea”的翻译来看,大观念与大概念、大想法、大思想等词语同义[2].威金斯和麦克泰格认为,大观念既是在一个研究领域中各种关系的核心,又是促使事实易于理解和有用的一个概念锚点;查尔斯指出,大观念是基于这一学科学习的核心观念(想法)[3];邵朝友、崔允漷指出,大观念居于学科的中心位置,集中体现学科课程特质的思想或看法;刘徽指出,大概念是反映专家思维方式的概念、观念或论题[4];顿继安、何彩霞认为大概念是指向具体学科知识背后更为本质、核心的概念或思想,它建立了不同学科知识间的纵横联系[5].
虽然有关“big idea”的表述各不相同,但是各学者的认识基本一致,他们主要从以下3个方面表述了大观念的基本内涵:第一,大观念之“大”表示的并非“广泛”,而是“核心”;第二,大观念不是基本概念或基本事实,而是能够反映基本概念或基本事实之间本质联系的概括性表述或学科思维;第三,大观念的表现形式多样,可以表现为“概念锚点”“观念(想法)”“思想”“看法”“概念”“论题”等,这些表现形式大体可分为3类:观念、思想、观点.
1.2 以大观念为中心的数学单元教学着力点
《课标》指出:“数学是研究数量关系和空间形式的一门科学”“数学源于对现实世界的抽象,基于抽象结构,通过符号运算、形式推理、模型构建等,理解和表达现实世界中事物的本质、关系和规律……”“数学承载着思想和文化,是人类文明的重要组成部分……”可见,《课标》阐述了数学的3方面特征:
第一,“数量关系和空间形式”体现了观察世界的数学眼光,反映了数学学科的研究视角.数学知识研究路径的基本要点是:背景(现实世界中的一类现象)—概念(研究对象)—性质(要素、相关要素之间的关系、变化规律等)—结构(相关知识的联系)—应用[6].这一研究路径也是人教A版《普通高中教科书·数学》(以下统称“教材”)编写的明线,反映了“事实—方法—方法论—数学学科本质观”这一专家思维方式.
第二,“抽象→推理(运算)→模型”体现了数学学科的研究顺序,反映了数学学科的基本思想.数学基本思想是对数学事实与理论经过概括后产生的本质认识,体现了知识和概念背后的内在联系,可以作为知识和概念的上层组织,具有奠基性、总结性和广泛性的特征.数学基本思想蕴涵在数学知识学习的过程中,既可以对教学观念进行指导,也可以对教学实践进行操作.
第三,数学本身就是一种文化,蕴含着数学的思想、精神、语言、方法、观点,以及它们的形成和发展,与人类人文活动紧密联系.融入数学文化的教学能有效回答“为什么要研究这个知识?怎么研究这个知识?这个知识有什么价值和意义?[7]”等教与学的问题,是培养学生创新思维和批判思维的重要途径.
基于上述分析,结合“观念”“思想”“观点”这3种大观念的表现形式,可以将“研究方法”“基本思想”“数学文化”作为数学单元教学的着力点.
2 以大观念为中心的数学单元教学策略
2.1 以研究方法为主题的单元教学策略及案例
2.1.1 以研究方法为主题的单元教学策略
以研究方法为主题组织单元,是指按照“背景—概念—性质—结构—应用”这一数学研究路径组织教学内容,将属性相同的研究对象串联成一个单元.这种单元以“研究方法”为大观念,有利于知识结构的形成.
教材中知识的呈现顺序往往与知识发生、发展的历史顺序不同,是按照知识的逻辑结构进行编写的,这样的编写方式有利于教学以“研究方法”为线索,挖掘知识发展顺序这一教学“暗线”.以研究方法为主题的单元教学以数学知识为学习载体,帮助学生掌握研究数学对象的一般方法,把教学目标从学生“学会”了哪些知识与方法转变为学生“会学”了哪些知识与方法,从而更好地把握知识之间的内在联系,形成一个逻辑严密连贯、结构功能良好的知识体系.
以研究方法为主题的单元教学基本结构如图1所示.
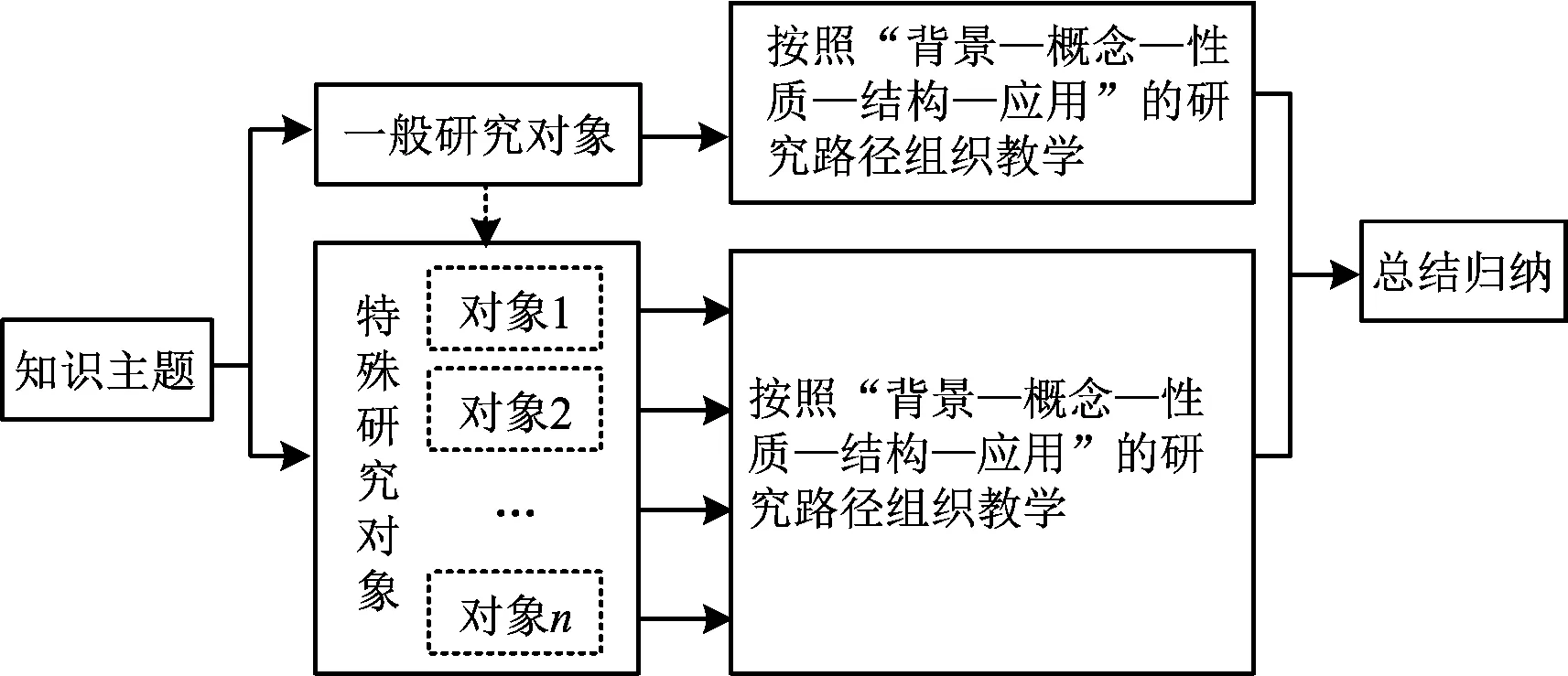
图1
其实施过程是:
1)将“研究方法”作为大观念,把知识主题分解为若干研究对象,包括一般研究对象和特殊研究对象;
2)按照研究方法进行一般研究对象的教学,明确学习新知识的一般路径与方法;
3)设计好知识的学习顺序,首先按照研究方法进行对象1的知识学习,然后类比对象1的学习过程学习其他知识,深化研究方法;
4)总结归纳,形成单元知识结构.
2.1.2 以研究方法为主题的单元教学案例设计
案例1函数单元整体教学设计.

基于上述教材分析,设计函数单元整体教学结构如图2所示,该单元结构分为3个子单元.
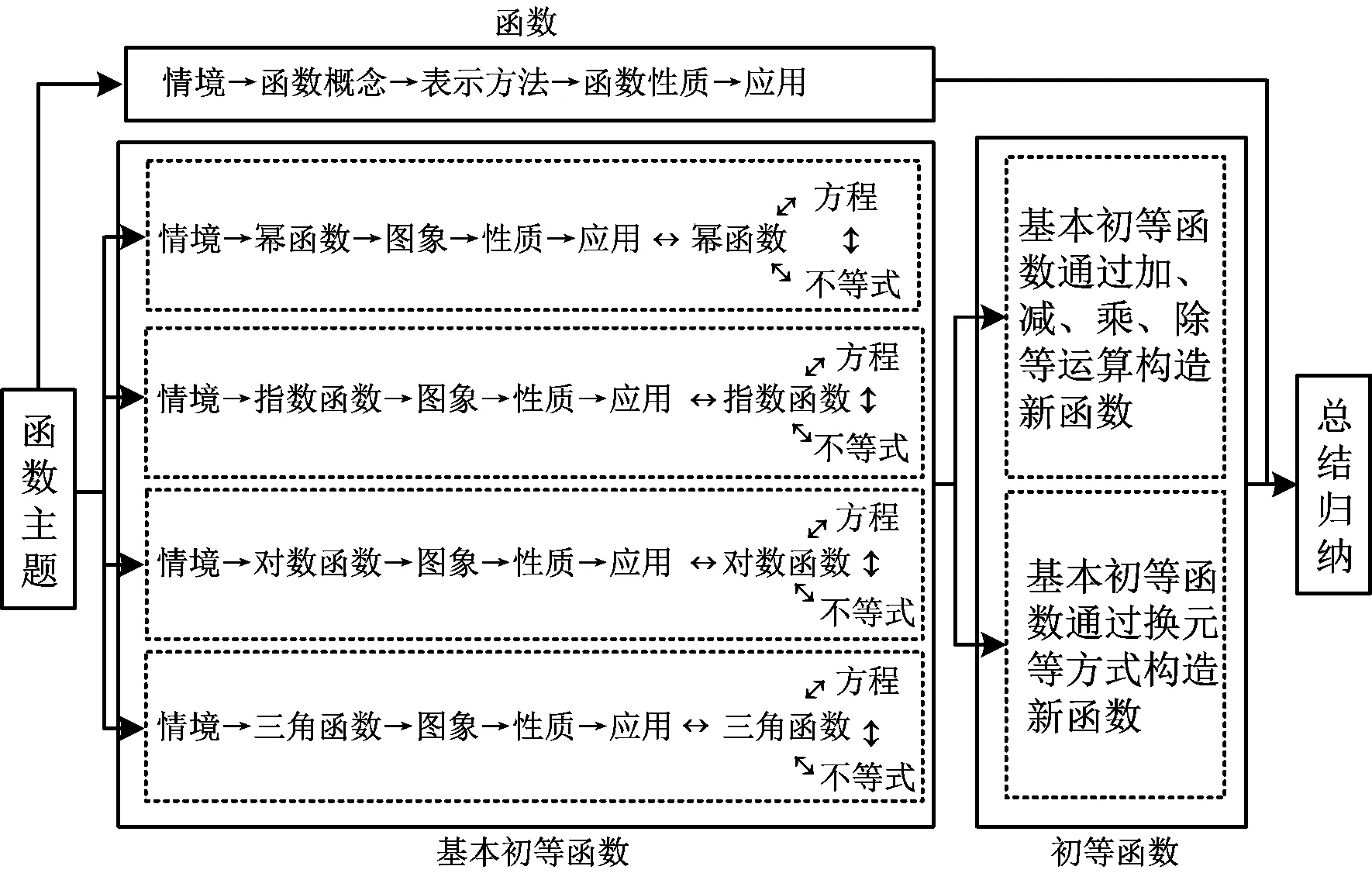
图2
第1个子单元是函数的概念与性质.为深化学生对高中函数概念的理解,在函数概念形成时,以现实问题为情境,引导学生分析具体实例,理解函数是两个变量的范围(非空数集A,B)与对应关系f构成的对应系统“f:A→B”,再学习解析式、图象、表格等表示方法,将学生初中通过定性表述的函数性质用定量刻画的数学语言进行精细化表达,并进行简单应用.这一子单元的教学既要巩固好基础知识和基本技能,也要提炼出研究方法,为后续具体函数的学习打好基础.第2个子单元是基本初等函数.每类基本初等函数的教学分别从实际问题情境中抽象出函数模型,再引导学生从理解函数概念的本质着手,归纳得到相应函数的一般表达式,并按照研究函数的一般方法学习其图象与性质,进而解决教学情境的实际问题,最后分别从函数与方程、不等式等角度进行知识关联,提高学生的整体认识,深化知识理解.每一类基本初等函数的教学都可以引导学生进行类比学习,教师应将研究方法贯穿于教学过程中.第3个子单元是初等函数.首先,教师要教会学生用运算的观点和换元的方法构造函数,进而掌握应用基本初等函数研究初等函数的图象与性质的方法;其次,教师要教会学生用运算和换元的眼光阅读函数解析式、推理函数的图象与性质.教学课时的安排需要配合第2个子单元的教学,紧跟在每一类基本初等函数的知识学习之后,引导学生由浅入深、类比迁移,不断完善认知结构,深化“研究方法”这一大观念.
2.2 以基本思想为主题的单元教学策略及案例
2.2.1 以基本思想为主题的单元教学组织策略
史宁中把数学基本思想归结为3个核心要素:抽象、推理、模型.三者既相对独立,又相互交融,是一个有机整体.以基本思想为主题组织单元,是指以“抽象、推理、模型”思想中的某一个为中心来组织教学内容,单元内容集中体现这一数学基本思想,指向学生学习迁移能力的提高.这种单元以“基本思想”为大观念,有利于数学核心素养的培养.
数学学科核心素养可分为3组:数学抽象,直观想象;逻辑推理,数学运算;数学建模,数据分析.分别称之为数学思维素养、数学方法素养、数学工具素养.这3组素养形成数学学科核心素养的3个层面[8].数学思维素养体现了数学思维的2种基本形式,对应基本思想“抽象”;数学方法素养体现了数学思维的基本方式,对应基本思想“推理”;数学工具素养体现了运用数学知识和方法解决问题的基本途径,对应基本思想“模型”.以基本思想为主题的单元教学,就是以数学基本思想为学习主题,帮助学生提高数学的关键能力.
以基本思想为主题的单元教学基本结构如图3所示.

图3
其实施过程是:
1)将“基本思想”作为大观念,确定一个数学基本思想为教学中心,适当选择其他数学基本思想为教学次中心;
2)明确深化该数学基本思想对应的单元内容,即学习载体类型:概念命题、方法技能、实际(数学)问题等,并以“线串式结构单元[9]”的方式组织系列单元内容;
3)围绕数学基本思想精心设计问题链、题组或问题,将单元内不同学习内容按照相似的教学程序进行教学实施;
4)组织学生在一组概念命题、方法技能、实际(数学)问题学习结束后,对这一单元的内容进行反思,总结共同规律,深化学生对数学基本思想的理解.
2.2.2 以基本思想为主题的单元教学案例设计
案例2立体几何初步“角的度量”单元整体教学设计.
《课标》在立体几何初步的内容要求中多次强调借助长方体学习基本图形的位置关系.一方面,长方体与教室等生活空间联系紧密,有助于学生通过直观感知学习新知;另一方面,长方体也是空间向量与立体几何学习的基础,有利于建立前后知识的联系.基本立体图形作为立体几何的学习载体,是重要的数学模型之一,因此,教师在关注位置关系和度量关系时,要加强对模型思想的渗透.此外,《课标》在立体几何初步的教学内容中对“度量关系(距离、角)”未有表述,教材中涉及“角的度量”的学习内容也不多.显然,异面直线所成的角(线线角)、直线与平面所成的角(线面角)、平面与平面所成的角(二面角)这3类角的概念学习重在服务“位置关系”的教学[10].
基于上述对《课标》和教材的分析,笔者设计立体几何初步“角的度量”单元整体教学结构如图4所示,该单元整体教学设计以推理思想为主、模型思想为辅,分3个课时的教学内容,分别是线线角的求法、线面角的求法、二面角的求法,3类角的求法(度量计算)按照“线串式结构单元”的方式组织教学.具体地,每个课时的教学都以正方体模型为载体,选定一个角的求法为教学主题.首先,引导学生观察、发现,并提出正方体顶点形成的线与线、线与面、面与面之间的位置关系及其所成角的大小(或余弦值)的度量计算问题,梳理形成教学的系列题组;其次,教师结合具体问题和角的概念分析并形成“作角”的方法,完成题组内所有角的度量问题的辅助线添加,再选择其中一个问题进行“作角、证角、求角”过程的规范表达,引导学生仿照例题示范进行其他问题的课堂演练;最后,结合各类角的研究过程与结果,总结3类角的求法,强化推理思想,同时以度量计算的结果反过来认识基本立体图形——正方体,深化模型思想.在教学中还可以类比上述基于正方体模型的角的度量的学习思路,将正方体变为长方体、正三棱柱等基本立体图形,丰富问题背景,强化“基本思想”这一大观念.

图4
2.3 以数学文化为主题的单元教学策略及案例
2.3.1 以数学文化为主题的单元教学组织策略
以数学文化为主题组织单元是指借助数学文化追根溯源,厘清知识的来龙去脉和知识之间的本质联系,进而按照知识发生、发展的顺序组织教学内容,指向科学精神的培养.这种单元以“数学文化”为大观念,有利于必备品格的养成.
与教材编写讲究知识的“科学性”不同,数学文化更彰显知识的“文化性”,包括产生某个知识的缘由是解决实际问题的需要还是数学理论发展的需要,其发生、发展过程蕴含了哪些数学思想方法、精神和价值等.以数学文化为主题的单元教学就是要跳出教材的限制,从数学文化的角度更大限度地挖掘知识的育人价值,进而重构教学逻辑,使得知识学习既符合知识的发生、发展顺序,又符合学生的心理认知规律,还能陶冶学生的道德情操.
以数学文化为主题的单元教学基本结构如图5所示.

图5
其实施过程是:
1)将“数学文化”作为大观念,选定知识主题,挖掘知识所蕴含的数学文化;
2)根据数学文化呈现的知识发生、发展的顺序重构知识学习顺序,并将知识主题分为若干子知识;
3)围绕数学文化,针对不同知识内容精心设计情境、问题、例题和习题等,发挥数学文化的育人价值;
4)总结反思,深化学生对数学文化的理解.
2.3.2 以数学文化为主题的单元教学案例设计
案例3圆锥曲线单元整体教学设计.
教材在章引言中介绍了圆锥曲线的截面定义,通过“拉线作图”引出椭圆,类比椭圆的第一定义将“和”变为“差”,利用信息技术探究引出双曲线;根据垂直平分线的性质,借助信息技术探究引出抛物线,通过例题介绍了圆锥曲线的第二定义.教材中知识的呈现有以下2个问题值得探讨:一是如何更好地实现由截面定义到第一定义的自然过渡;二是如何更好地揭示圆锥曲线的内在统一性.通过对圆锥曲线的历史考察可知[11-12],其历史大致可以分成圆锥曲线的发现、截面定义的形成、基本性质的推导、焦半径性质的获得、机械作图的产生、轨迹定义的确立和标准方程的推导这7个重要环节[11].其中,圆锥曲线的发现与太阳照射日晷的影子有关,圆锥曲线定理的统一性的证明与Dandelin双球模型紧密联系,圆锥曲线标准方程的推导除了教材中呈现的两次平方法,还有“和差术”法、“平方差”法、“分子有理化”法、“余弦定理”法[13]等.根据圆锥曲线知识的历史顺序和教材顺序,将教学顺序进行重构,如图6所示.
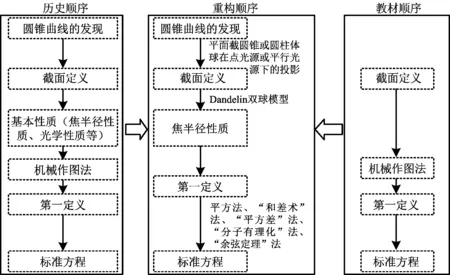
图6
根据上述教学重构顺序,设计圆锥曲线单元整体教学结构如图7所示,该单元整体教学设计按照“总—分—总”的方式将教学分为3个阶段.第1个阶段为3种圆锥曲线第一定义的学习:通过创设球在点光源下投影的情境,介绍圆锥曲线的截面定义,再结合光学性质将情境抽象成Dandelin双球模型,统一学习3种圆锥曲线的概念,引出单元学习内容.第2个阶段为椭圆、双曲线、抛物线这3个子单元的学习:3个子单元教学结构一致,均是先学习标准方程,再学习简单几何性质,双曲线、抛物线子单元的教学均可类比椭圆子单元的教学.在推导标准方程的教学中,通过融入数学文化视角下的推导方法,引导学生感悟数学家们的智慧.第3个阶段为单元总结反思:一方面,总结所学知识,形成知识方法体系;另一方面,引导学生深刻感悟数学文化,了解3种圆锥曲线的统一定义等,内化“数学文化”这一大观念.

图7
3 结语
上述讨论的3种“以大观念为中心的数学单元教学策略”分别体现了单元教学的3个维度.实际上,在教学实施过程中并不意味着只能采取某一种教学策略,而是3种教学策略可以同时应用,统一体现在完整的教学活动中.当3种教学策略作用于同一知识板块且属性相同的研究对象时,不妨优先以“研究方法”为主题,按知识发展顺序组织单元教学,再以“基本思想”为主题,按知识发展阶段嵌入单元教学,最后将“数学文化”融入单元教学.总体来看,3种教学策略融合应用,“研究方法”促进知识体系的构建,“基本思想”促进数学学科核心素养的培养,“数学文化”促进必备品格的养成.

