挖掘试题育人价值 发展学生几何直观素养
——以“黄金分割”为例
李 卓
(杭州市开元中学,浙江 杭州 310008)
几何直观素养的形成与发展有助于提升学生运用图形描述、分析和解决数学问题的能力.初中阶段图形与几何领域强调在用几何直观理解几何基本事实的基础上,从基本事实出发推导图形的几何性质和定理;强调从运动变化的观点来研究图形;强调数形结合,用代数方法研究图形.由此可见,初中阶段对于学生几何直观素养的要求很高.几何直观素养与推理能力、空间想象能力等其他核心素养之间具备整体性的协同发展特征,联系紧密.本文通过分析黄金分割试题,阐述如何引导学生挖掘图形的本质特征,从图形特征转化为代数表达,提升复习课的整体性和高效性.
1 黄金分割及其学习价值
黄金分割被称为“最美丽”的几何比率,被广泛应用于建筑、绘画、雕刻等领域.不同版本的教材均设置了黄金分割的相关学习内容,如人教版《义务教育教科书·数学》(八年级下册)中设置了“黄金比和建筑”相关内容,浙教版《义务教育教科书·数学》(九年级上册)中设置了“建筑中的美与黄金分割”等内容[1].

黄金分割的美内蕴于其发现的背景图形,同时外化为具有类似数学结构的生物空间[2].数学中有许多具有黄金比的几何图形,如黄金三角形、黄金矩形等.黄金三角形是具备特殊角的等腰三角形,一类是顶角为36°的等腰三角形,它的底边与腰之比为黄金比;另一类是顶角为108°的等腰三角形,它的腰与底边之比为黄金比.黄金矩形的宽与长之比满足黄金比.黄金图形因具有良好的图形结构和线段比例,在主题学习中经常被采用.
初中阶段主要以平面几何图形为研究对象,学生需学习几何图形自身固有的性质和图形之间的关系,即研究构成几何图形的要素之间的数量关系、位置关系中的不变规律以及探索不同图形之间的联系(如图1).
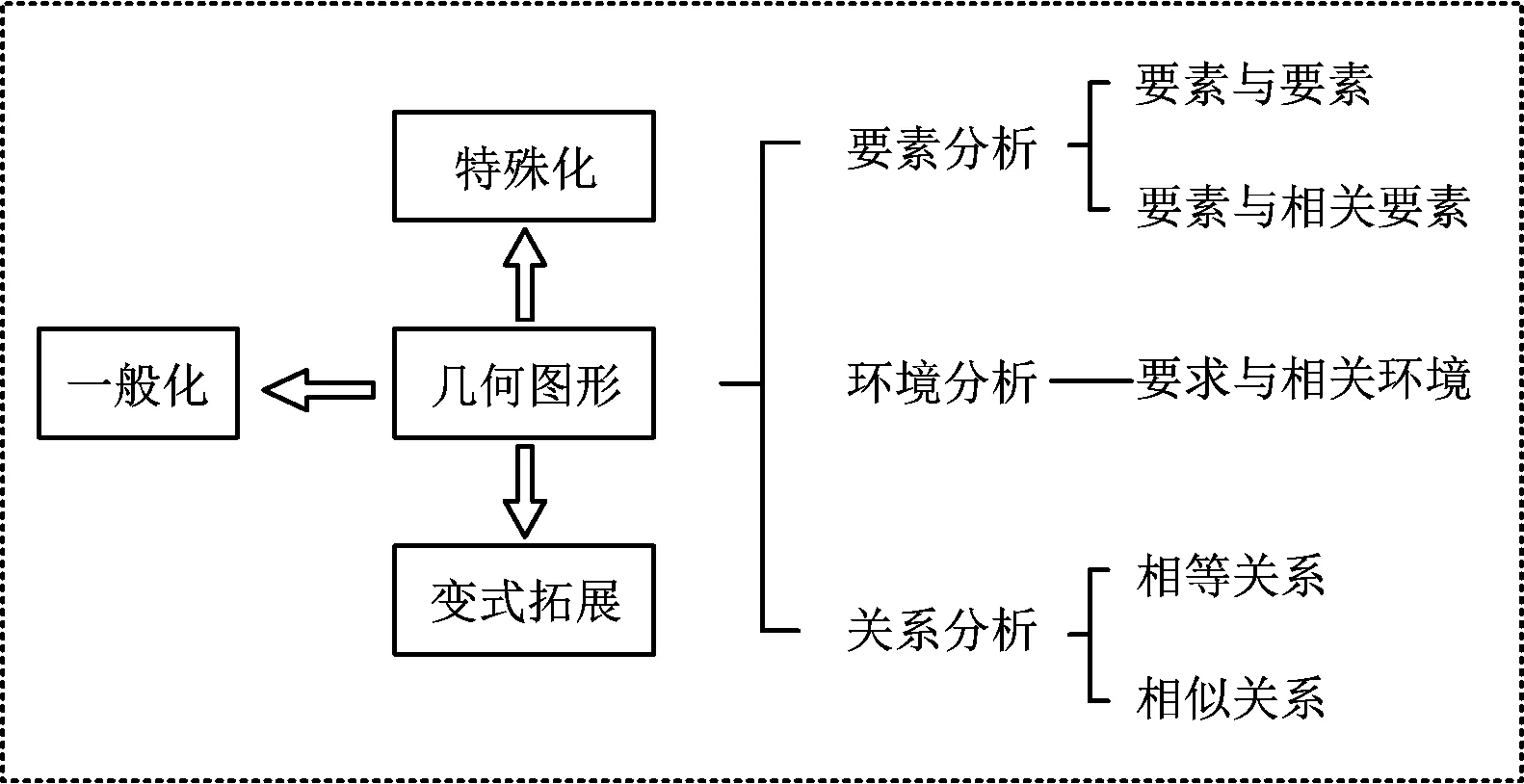
图1
黄金分割不仅是研究线段之间的比例关系,还可以在相似三角形、特殊平行四边形、圆等几何图形中研究相等关系和相似关系等.通过研究复杂图形中的黄金分割,可以将零散的知识点联系起来,有效整合数学知识和技能,准确把握学科核心内容和核心任务[3],提升学科核心素养.
2 数学试题中“黄金分割”的呈现形式及特征
《义务教育数学课程标准(2022年版)》(以下简称《课标》)提出,义务教育阶段的学业质量评价要求以结构化数学知识主题为载体,在形成与发展“四基”的过程中发展抽象能力、几何直观、推理能力等核心素养,从学生熟悉的生活与社会情境,以及符合学生认知发展规律的数学与科技情境中,经历“三会”的完整过程,经历数学的学习运用、实践探索活动的经验积累.正因为如此,以黄金分割为背景的试题也在中考中屡见不鲜.
笔者以近几年杭州数学中考中以黄金分割为背景的试题进行讨论与分析.
2.1 “开门见山”式
“开门见山”式试题是指在几何图形中直接或者显性地具备黄金图形结构的题目.学生可以借助黄金图形的相关性质进行研究,如例1和例2中图形均蕴含了黄金三角形.
例1如图2是一张矩形纸片ABCD,点M是对角线AC的中点,点E在边BC上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,联结DF,EF.若MF=AB,则∠DAF=______.

图2
(2021年浙江省杭州市数学中考试题第16题)
解法1如图2,联结DM,易知
DM=MC=AM.
因为MF=AB,所以
MF=DC=DF.
设∠DAC=x,则
∠DMF=∠MDF=2x, ∠DFC=∠DCF=4x.
在Rt△ADC中,
∠DAC+∠DCF=90°,
即
x+4x=90°,
得
x=18°,
故
∠DAF=18°.
解法2设元过程同方法1,略.在△MDC中,
∠DMC+∠MDC+∠MCD=180°,
即
2x+4x+4x=180°,
得
x=18°,
故
∠DAF=18°.
评注此题在矩形背景下通过折叠进一步得到更多的对应角和线段相等,从而满足较多的关于角和线段的等量关系.事实上,△MDC和△DCF均是顶角为36°的黄金三角形,因此具备十分良好的结构特征.若学生能发现黄金图形,则能更加快捷地得到解题的突破口.

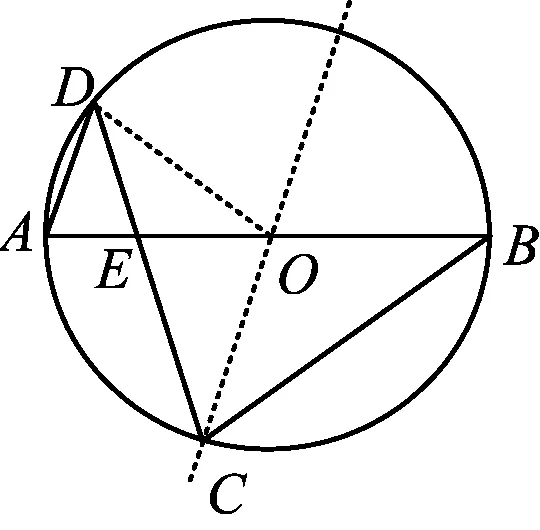
图3
(2022年浙江省杭州市数学中考试题第16题)
解如图3,根据圆的相关性质和折叠的意义,易知
AD=ED,CE=CO,BE=BC.
设∠B=x,则
∠OCB=x, ∠DAE=∠DEA=2x,
∠BEC=∠BCE=2x.
在△BEC中,
∠BEC+∠BCE+∠B=180°,
即
x+2x+2x=180°,
得
x=36°,
故
∠B=36°.
联结OD,易得
AD=ED=EO.
易知△BEC,△OEC,△ADE均为黄金三角形,从而
于是
评注此题以圆形为背景,通过圆心角定理和圆周角定理等得到许多相等的角.借助折叠的轴对称性又可以得到对应角相等,故此题中有较多的等腰三角形.通过第1)小题求得的36°角,可以发现△BEC,△OEC,△ADE均为黄金三角形,因此第2)小题求BC与AD的比值可以通过两次相似变换得到,即两次利用黄金比.这样的解题路径自然流畅,学生能根据图形的结构特征充分挖掘图形中不同线段之间的紧密联系.
2.2 “抽丝剥茧”式
“抽丝剥茧”式试题是指图形中不能直接得到黄金图形,但在给定条件下满足黄金分割的题目.例如,例3在给定条件tanα=tan2β下,可知点E为AF的黄金分割点.
例3第24届国际数学家大会会徽的设计基础是1 700多年前中国古代数学家赵爽的“弦图”.如图4,在由4个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)和中间一个小正方形EFGH拼成的大正方形ABCD中,∠ABF>∠BAF,联结BE.设∠BAF=α,∠BEF=β,若正方形EFGH与正方形ABCD的面积之比为1∶n,tanα=tan2β,则n=
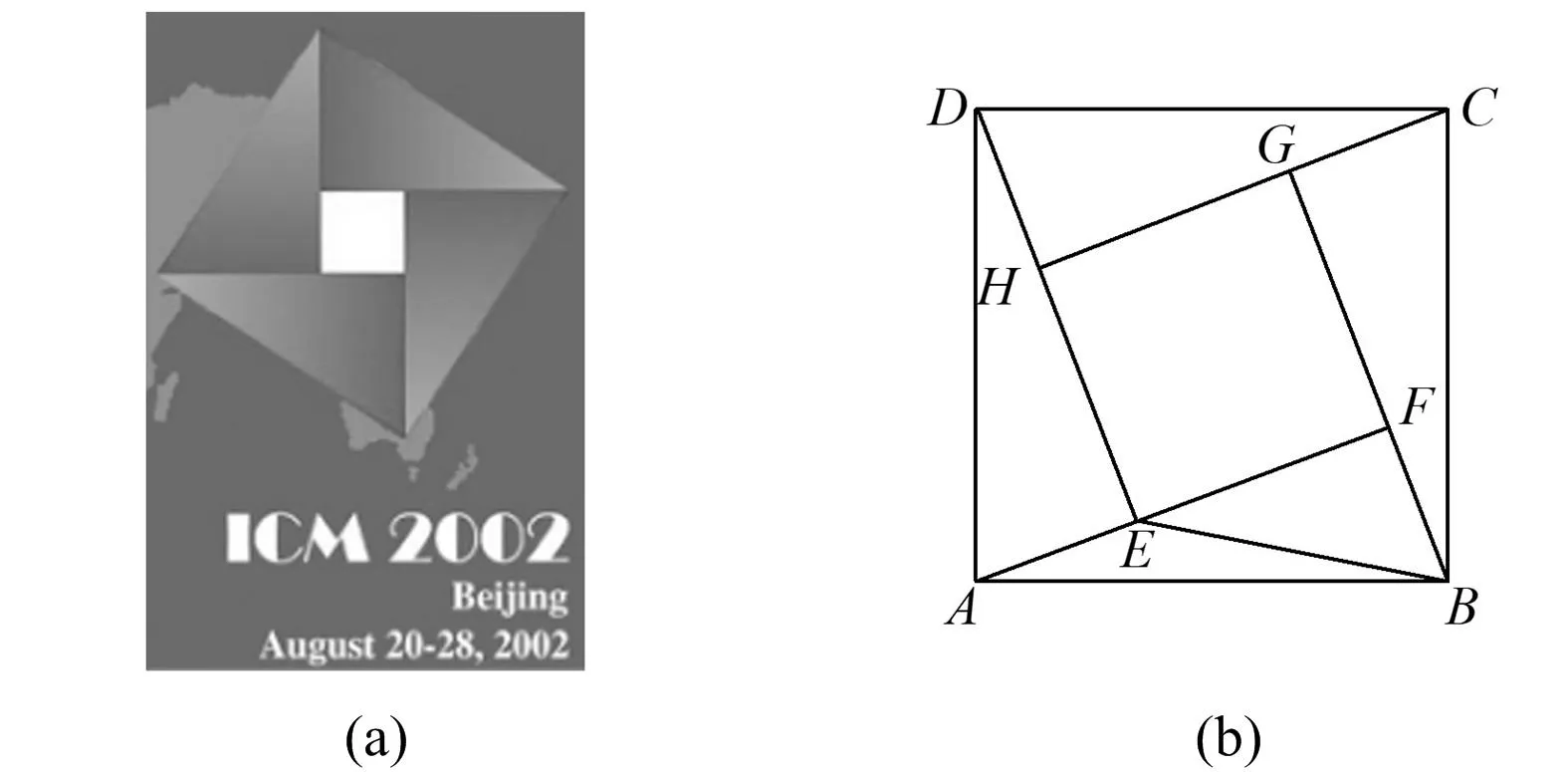
图4
( )
A.5 B.4 C.3 D.2
(2023年浙江省杭州市数学中考试题第10题)
解法1设AE=1,EF=x,则
BF=1,AF=1+x.
从而
进而
于是
x2=1+x.
由题意,得
故
n=3.
解法2设AE=a,AF=b,则
BF=a,EF=b-a.
从而
进而
得
ab=(b-a)2,
即
a2+b2=3ab.
由题意,得
故
n=3.
解法3设正方形EFGH的面积为S1,正方形ABCD的面积为S2,4个全等的直角三角形(△DAE,△ABF,△BCG,△CDH)的面积均为S.
设AE=a,AF=b,则
BF=a,EF=b-a.
从而
进而
即
ab=(b-a)2,
于是
S1=2S,
得
S2=S1+4S=6S,
即
故
n=3.
解法4由题意,得
从而
于是
EF2=AF·BF.
由题意知AE=BF,从而
EF2=AF·AE,
即点E为AF的黄金分割点.
设EF=x,则
由勾股定理,得
从而
故
n=3.
评注此题以中国古代数学家赵爽的“弦图”为背景,贴近学生的学习生活.解法1和解法2都是先设线段的长度为未知量,进而表示出相关角度的正切值,再根据大正方形和小正方形的面积关系得到等量关系,利用消元的方法进行计算.解法3是从弦图中大正方形、小正方形和直角三角形的面积关系出发,借助完全平方公式的恒等变形进行分析,两个正方形的面积均可以用直角三角形进行表示,进而解决问题.解法4则是从条件tanα=tan2β出发,通过等式变形后得到点E为AF的黄金分割点,从而发现图形中多处线段成黄金比.教学时需要充分挖掘图形中线段之间的关系,让学生感悟不同解题路径的联系与区别,从而更有序地进行思考,提升学力.
2.3 “循序渐进”式
“循序渐进”式试题是指可通过相似三角形、三角函数等方法得到相应的线段比例关系,再通过线段的转化得到特殊的线段比例关系,然后根据定义得到黄金分割的题目.
例4如图5是一张矩形纸片,点E在边AB上,把△BCE沿直线CE对折,使点B落在对角线AC上的点F处,联结DF.若点E,F,D在同一条直线上,AE=2,则DF=______,BE=______.
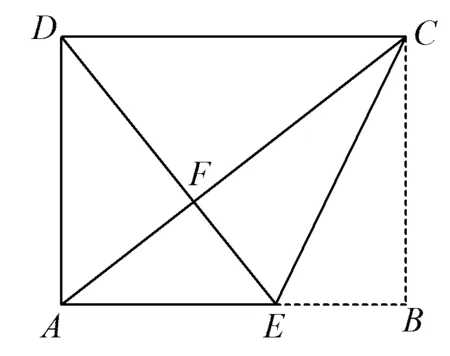
图5
(2020年浙江省杭州市数学中考试题第16题)
解法1设BE=x,由折叠和矩形的性质可知
EF=x,DC=AB=2+x,
且
∠DCE=∠CEB=∠CED,
得△DCE为等腰三角形.则
DE=DC=2+x,DF=2.
由△CDF∽△AEF,得
即
解得

故
解法2由题意得
AE=DF=2,DE=DC.
由△AEF∽△CDF,得
进而
DF2=EF·DE,
即点F为DE的黄金分割点,因此点E为AB的黄金分割点,得
故
解法3DF的求解同解法2,下面求BE.由题意得
AD=CF,DE=DC.
由△ADF∽△ACD,得
即
AD2=AC·AF,
进而
CF2=AC·AF,
从而点F为DE的黄金分割点,于是
又
得
故
评注解法1通过设未知线段BE为x,利用矩形和折叠的性质得到相等的线段和角,再借助相似三角形得到线段之间的等量关系,从而解出x的值.解法2和解法3借助不同的相似三角形性质发现点E,F分别为相应线段的黄金分割点,从而根据黄金比得到未知线段的长度.此题中有多个直角三角形,而且均是相似三角形,故可以在发现黄金分割点的基础上,利用三角函数进行线段之间的转化,也能较容易地得到未知线段的长度.
3 教学启示
3.1 挖掘图形特征,关注复习课的整体性
图形与几何的复习不能停留在单一的知识点上,要注重知识之间的联系,从知识的整体和结构入手,挖掘复杂图形中蕴含的图形特征,转化为对应的代数表达(如图6).例如,上文提及的几道历年中考真题,黄金分割蕴含在三角形、矩形、正方形、圆等图形之中,需要学生能通过这些图形的性质以及折叠等条件发现相互之间的联系,做到“图形在变、方法不变、结论类似”,从而有效提高几何复习的整体性.
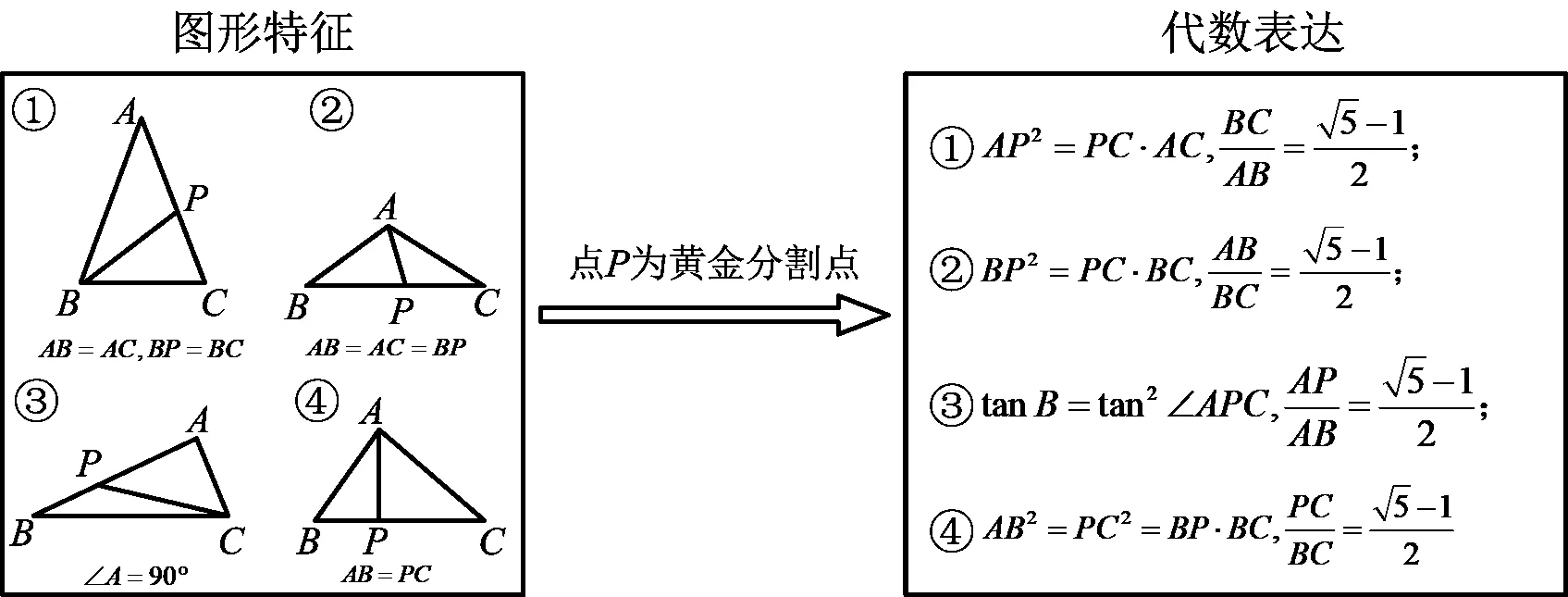
图6
3.2 开展主题学习,提升复习课的综合性
《课标》要求通过主题学习,设计数学学科内部不同领域或者单元之间的综合学习,学生在真实情境中面对具有挑战性的任务,能发现问题和提出问题,综合运用数学思想方法分析和解决问题.几何复习教学时围绕黄金分割开展主题学习,可以让学生感悟从数学的角度发现和提出真实情境中的问题,用数学的思维综合地、有逻辑地分析问题、解决问题,积累数学活动经验,体会数学的科学价值,发展实践创新能力.
3.3 融入数学文化,发挥数学的育人价值
黄金分割是经久不衰的数学研究内容,是数与美的结合点,体现了优美的几何直观和丰富的代数内涵的统一,从古至今在各个领域都具有广泛的应用.通过数学教育与数学史、数学文化的深度融合[4],让学生感悟古人的智慧与创造,有助于正确引导学生的价值观,增强其文化自信与民族自豪感,真正发挥数学的育人价值.

