模型观念下分析图形结构,探寻解题路径
——2023年温州中考数学卷第24题解法探究与启示
林 依, 易良斌
(1.杭州市澎扬中学,浙江 杭州 310015;2.杭州市上城区教育学院,浙江 杭州 310009)
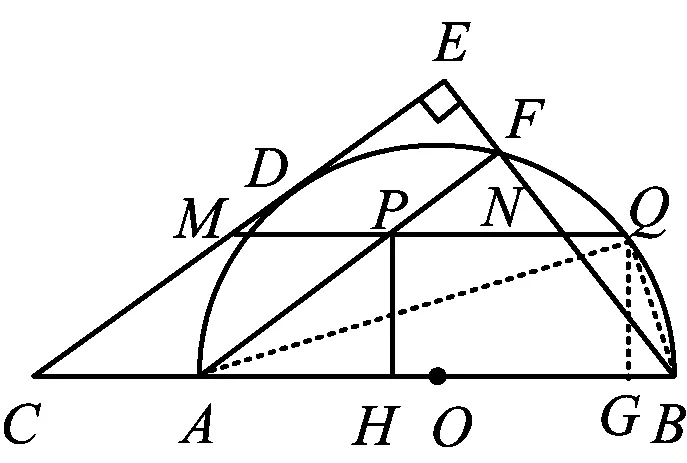
在初中阶段的数学教育教学实践中,中考数学试题发挥着特殊而又重要的作用.2023年浙江省温州市数学中考命题坚持素养立意,凸显育人导向,正确反映新时代数学教育改革和学生发展的需要,考查学生数学基础知识、基本技能和基本思想方法.其中第24题以圆为主图,辅以相切的直角三角形为图形背景,利用不同基础模型有效寻得解题途径,考查学生的核心素养.
1 试题呈现及其原型

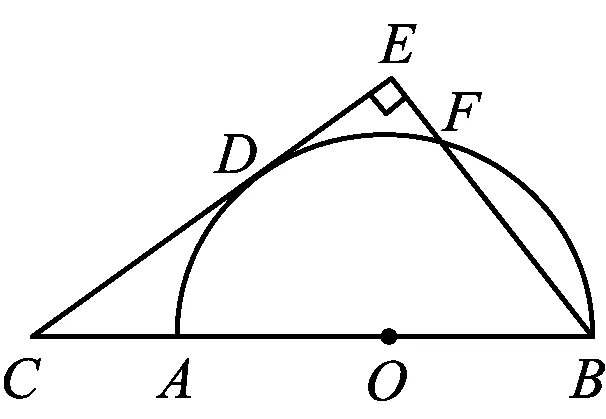
图1
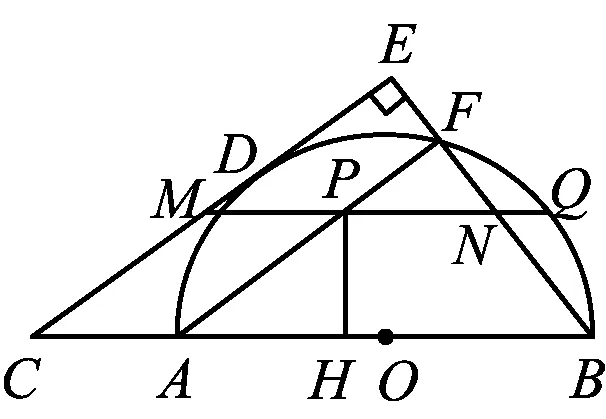
图2
1)求CE的长和y关于x的函数表达式;
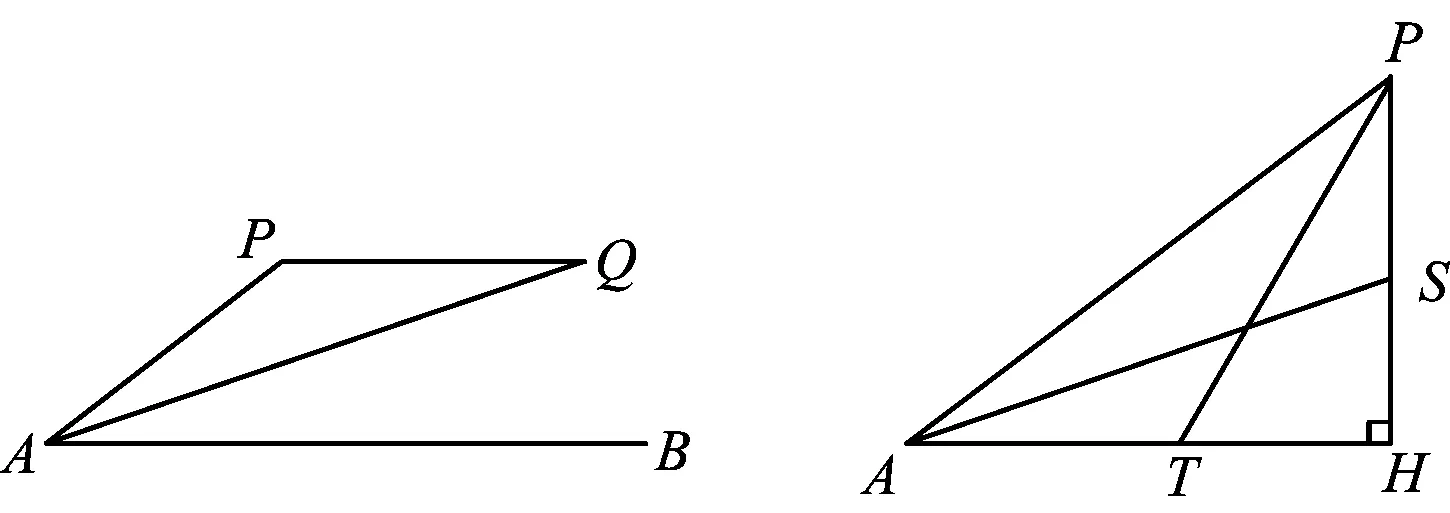
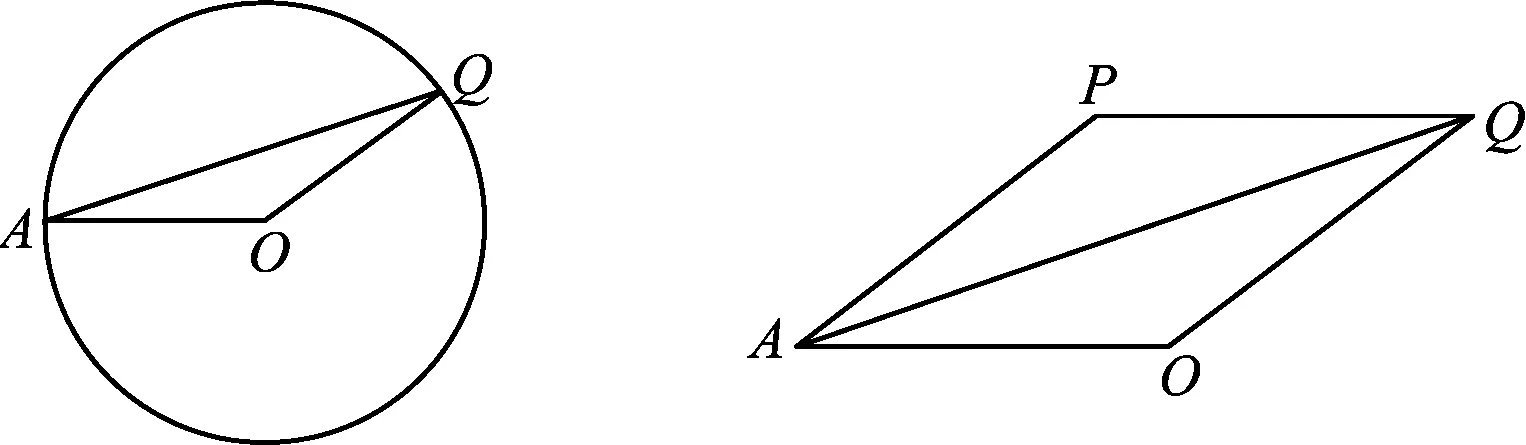
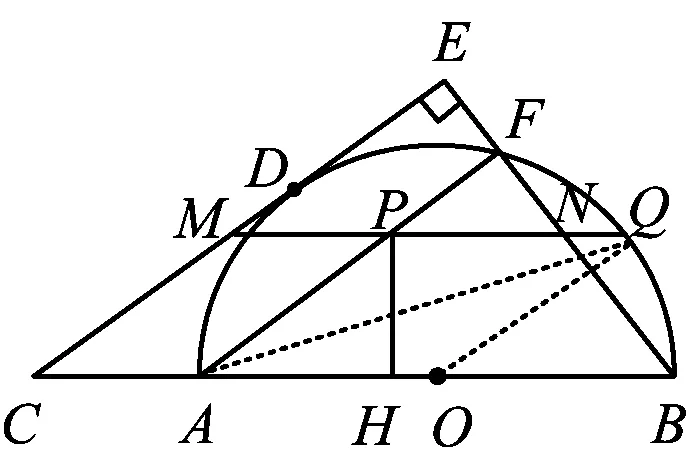
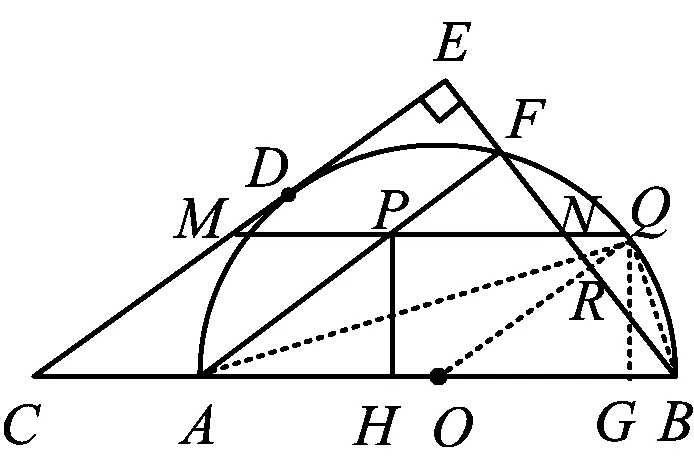
2)当PH (2023年浙江省温州市数学中考试题第24题) 试题原型来自浙教版《义务教育教科书·数学》(九年级下册)第43页课后作业题第5题: 例2如图3,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F.已知AC=12,BC=9.求AO的长. 图3 例2利用相切结合半圆与直角三角形两个基本图形,考查学生通过添加半径,构造相似图形这一基础模型的能力,并获得比例式进行求解计算. 例1在例2的基础上,以同样的几何图形为背景,进一步拓展延伸,综合考查了圆、直角三角形、相似三角形、直线与圆相切的概念、性质、关系和规律,以及图中部分线段长度之间的函数关系.该题涉及分类思想、方程思想、函数思想和数形结合思想,主要考查学生的推理能力、几何直观、运算能力、模型观念等核心素养[1]. 相较于第1)和第2)小题,第3)小题是该试题的难点.学生容易理解NQ与PH之间的变量依存关系,但在求MN的长度时需要探究变化过程中的不变量.学生往往会将“不变量”联想到具体数值上,却忽视了“不变量”也可能体现在确定的图形中,而利用辅助线探究图形的特殊性也是学生的薄弱点. 以圆和直角三角形为背景图形的几何问题可通过添加辅助线建立基本模型来形成解题思路. 模型1半弦直角构建垂径定理基本模型. 在圆内与弦有关的问题,可以构造弦心距、弦的一半和半径所形成的直角三角形,如图4所示. 图4 方法1如图5,联结OQ,作OR⊥MQ于点R,可知RO=PH=x. 在Rt△APH中,HP∶AH∶AP=3∶4∶5(在前面小题的解答中已求得),且PH=x,可得 因为四边形APMC为平行四边形,所以 MP=CA=1. 在Rt△ROQ中, RQ2+RO2=OQ2, 从而 解得 故 评注NQ是半圆O的弦的一部分,PH的长度等于弦心距,由此考虑构造半径、弦心距和弦的一半所形成的直角三角形的基本模型,寻得NQ与PH的数量关系,通过线段长度的转换,顺利解题. 模型2圆内接直角三角形和直角三角形斜边高模型. 圆内出现直径,可构建直径所对的圆周角,从而构造直角三角形,如图6所示.在直角三角形中构造斜边上的高线也是常见的基本模型,如图7所示,从中也可提取许多关于线段和角的数量关系. 图6 方法2如图8,联结AQ,BQ,作QG⊥AB于点G,可知 图8 QG=PH=x, 在Rt△APH中, 即 由于AB是直径,可知 ∠AQB=∠QGB=90° , 从而 于是 进而 即 故 评注将线段PQ的长度下移到线段AB上,利用直径AB构造Rt△ABQ,同时构造斜边AB上的高线QG,利用其中的相似三角形获得等角、成比例线段等几何关系,最终在线段AB上寻得含x的等量关系. 模型3双平模型和12345模型[2]. 图9 方法3如图8,联结AQ,BQ,作QG⊥AB于点G,可知 QG=PH=x. 在Rt△APH中, 则△APQ是等腰三角形.由MN∥AB,可得 ∠PAQ=∠PQA=∠QAB, 即AQ是∠PAB的平分线.在Rt△APH中, HP∶AH∶AP=3∶4∶5, 根据12345模型可知 后续同方法2,略. 模型4利用半径等腰三角形和菱形. 圆上的弦(非直径)与弦的两个端点和圆心连成的两条半径可以构成等腰三角形,如图11所示.菱形也可以看作由两个等腰三角形拼接而成,如图12所示. 图11 方法4如图13,联结AQ,OQ,可知AO=OQ,延续方法3中证得的等角,得 图13 ∠PAQ=∠PQA=∠QAB=∠AQO, 从而 OQ∥AP, 于是四边形AOQP是菱形,故 AP=AO, 即 解得 故 评注在方法3中发现△APQ为等腰三角形,且半径AO是∠QAB一边上的一部分,可以利用半径AO在等腰△APQ的下方构造半径等腰三角形的基本模型.同时,等腰△APQ和等腰△AOQ共用边AQ,且PQ∥AO,因此可证得菱形AOQP.如此,可利用菱形的邻边相等获得含x的最简等量关系. 模型5垂径模型和等腰三角形两腰高线模型. 如图14所示是垂径定理及其逆定理的基本模型,如图15所示是等腰三角形两腰上的高线相等的基本模型. 图14 方法5如图16,联结AQ,OQ,其中OQ交BF于点R,联结QB,作QG⊥AB于点G,可知 图16 QG=PH=x. 由方法3,得 ∠PAQ=∠PQA=∠QAB, 由垂径定理可知 OQ⊥FB, 从而 因为OQ=OB,即△OBQ是等腰三角形,且QG和BR是两腰上的高,所以 QG=BR, 即 因此 通过上述的解题思考,对于日常教学有以下启示. 在日常教学中,教师需要帮助学生熟悉基本图形的常用基础模型.以圆为例,常见模型有垂径定理模型、圆半径所构成的等腰三角形、弦心距所在的直角三角形等[3].在解决以圆为背景的几何问题中,可以尝试套用上述的常用模型,有助于寻找解题思路. 几何问题的复杂性往往是多个基础图形叠加而成的,而学生不善于对其进行剥离,从而产生解题障碍.教师在日常的教学中要注重对图形的构成过程进行分析,引导学生快速识别其中的基础图形,从而能够在复杂图形中剥离出基础模型. 在解决较复杂的几何问题时,有时需要辅助线的神来之笔.辅助线的添加往往能够构造出解题所需的基础模型.在日常的教学中,需关注学生添加辅助线的经验积累,有助于学生在实际解题中产生合理联想,快速找到解题思路. 几何问题是培养学生推理能力的有效载体,对培养学生严谨的推理能力、直观想象能力、分析和解决问题的能力有着不可替代的作用.特别是推理能力的培养,需要借助适切的典型试题.借助问题变式,联结方法,打通一类问题,让学生的认知更加全面且深刻.因此,在平时的教学中,教师要专注问题关联,探索解法的自然生成,从而有效发展学生的数学素养.
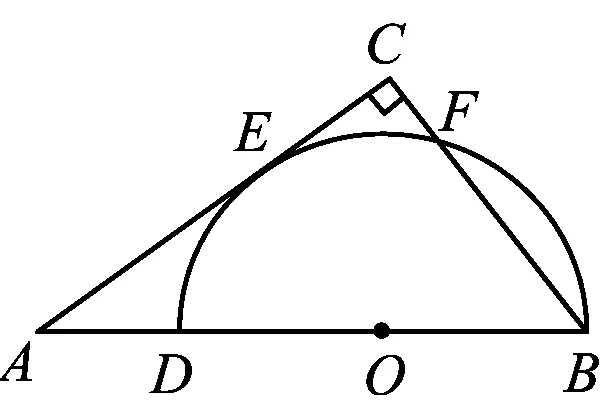
2 解法探究

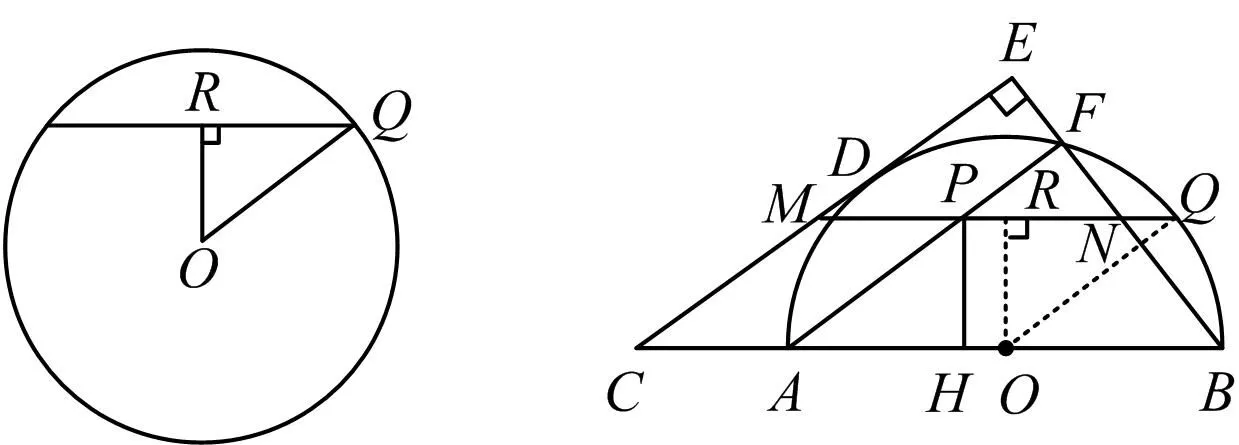


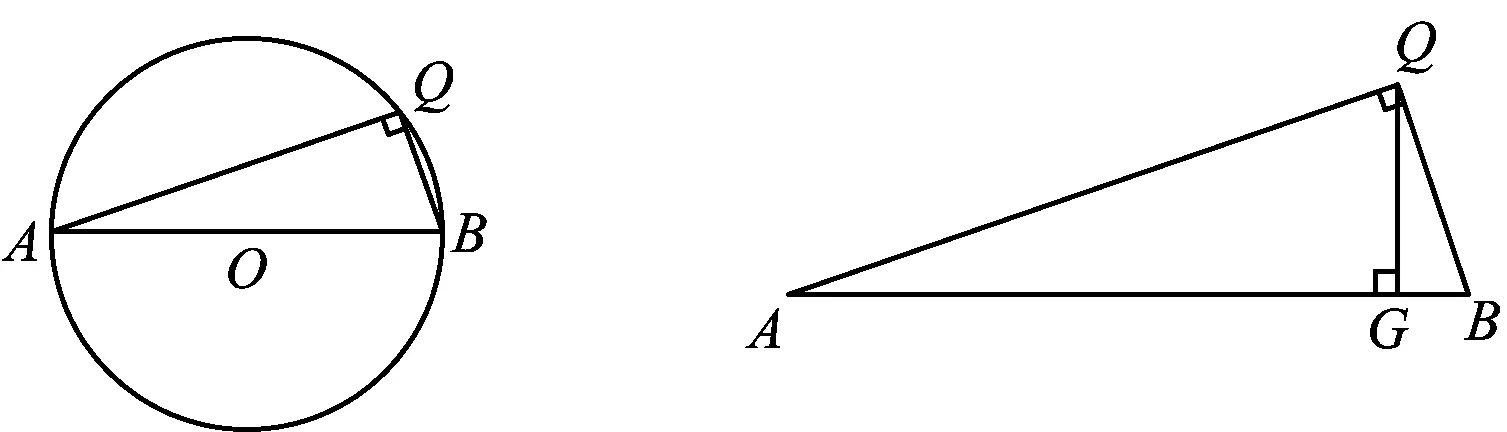
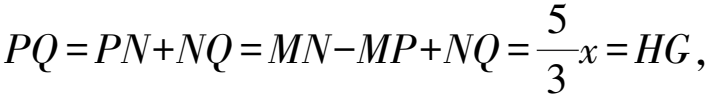
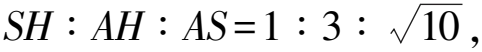

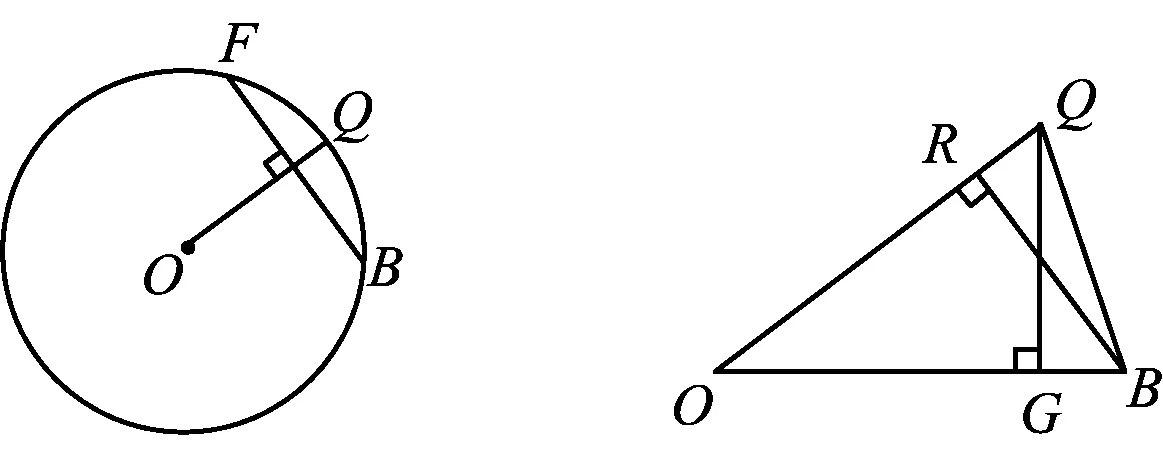
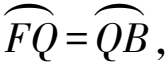
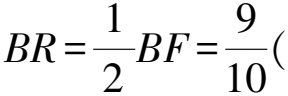

3 教学启示
3.1 熟悉基础模型,熟练运用模型
3.2 分析复杂图形,剥离基础模型
3.3 善于添加辅助线,构造基础模型
3.4 注重问题关联,发展数学素养

